GPS單頻實時動態定位研究與實現

周 鵬，劉 暉，2，錢 闖

(1.武漢大學衛星導航定位技術研究中心，湖北武漢430079;2.武漢導航與位置服務工業技術研究院，湖北武漢430075)

一、引 言

通過時間更新過程和量測更新過程，卡爾曼濾波對待估參數進行預測與修正，由于卡爾曼濾波的整個更新過程是循環遞推的，因此濾波器無須存儲太多的歷史數據，使用當前觀測數據即可實時獲得被估計參數的最優估計值。由于這個特點，卡爾曼濾波從一提出就受到各工程應用領域的青睞，尤其是實時動態數據處理領域，如高精度組合導航［1］與GPS動態定位。

在城市峽谷等復雜觀測環境下，由于衛星信號遮擋嚴重，可見衛星數量不多且衛星可視情況并不連續，加上復雜環境下多路徑效應等外部干擾因素的影響，不易確定觀測序列噪聲特性，這對濾波器的穩定性和模型精度有了更高的要求。針對這個缺陷，本文提出了觀測序列噪聲方差-協方差陣的自適應確定方法，對動態卡爾曼濾波算法進行了優化，加上原始觀測量的粗差探測。多次路測試驗表明，該算法穩定可靠，在普通的城市道路上，優化算法能顯著提高GPS動態定位的效果，得到較為理想的定位結果。

二、GPS動態卡爾曼濾波模型

1.卡爾曼濾波參數估計原理

利用卡爾曼濾波進行動態系統參數估計首先需要確定系統的狀態方程和觀測方程，對于離散線性系統，通用的卡爾曼濾波狀態方程和觀測方程為［2-3］

式中，Xk為 tk時刻的系統狀態向量;Φk，k－1為 tk－1至tk時刻的系統狀態轉移矩陣;Γk－1為系統噪聲驅動矩陣;Wk－1是動態噪聲序列;Zk為tk時刻的觀測向量;Hk為觀測方程系數陣;Vk為觀測噪聲序列。

系統隨機模型滿足以下要求

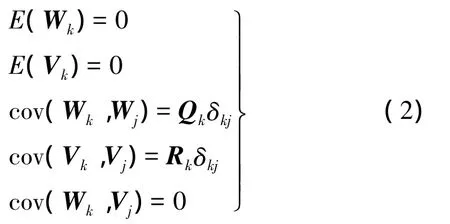
式中，Qk為動態噪聲序列Wk－1的方差-協方差陣;Rk為觀測噪聲序列 Vk的方差-協方差陣;δkj為 Dirac 函數［2］。

若狀態向量Xk與觀測向量Zk滿足式(1)，動態噪聲序列Wk－1與觀測噪聲序列Vk滿足式(2)，且動態噪聲方差-協方差陣非負定，觀測噪聲方差-協方差陣正定，則tk時刻狀態向量Xk的估計值

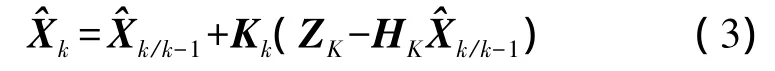
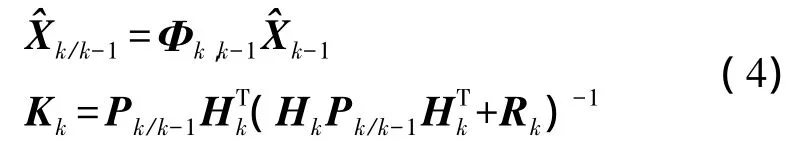
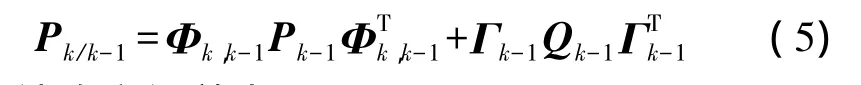
估計均方誤差為

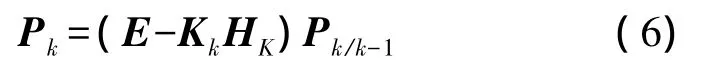
2.動力學模型的構建

對于GPS動態定位，由于信息的缺失，難以構建精確的動態定位模型來描述載體的運動，在損失一定精度的條件下，可對載體運動模型進行簡化，本文采用應用較多的常速模型(CV模型)［4］。

CV模型中選定狀態向量為

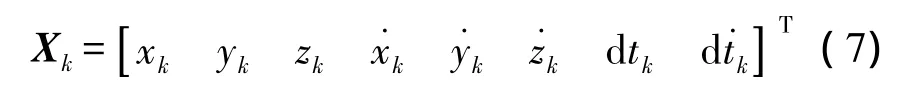
式中，(xk，yk，zk)為接收機的WGS-84地心坐標分別為接收機3個方向上的速度;dtk、d˙tk分別為接收機鐘差與鐘差變化率。

根據式(1)，可知狀態轉移矩陣 Φk，k－1為

據文獻［5］可知，動態噪聲序列 Wk－1的方差-協方差陣Qk為

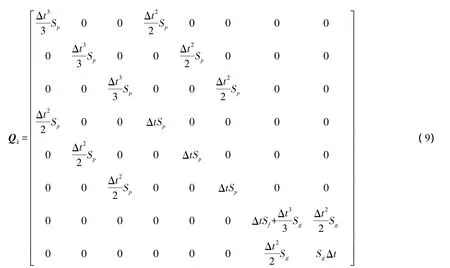
式中，Sp、Sf、Sg分別為接收機狀態、鐘差、鐘差變化率的譜密度，分別取值 1.0、0.4×10－18、1.58×10－18［5］。

濾波過程中，使用偽距單點定位結果作為濾波初始值。另外，當較長時間無法定位(衛星數不足)時需重新初始化。

3.觀測模型的構建

關于GPS觀測方程，給出其定義如下［6］

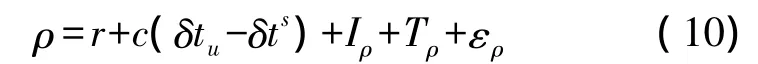
式中，ρ為偽距觀測值;r、c分別為衛星與接收機間的幾何距離和光速;δtu、δts分別為接收機鐘差與衛星鐘差;Iρ、Tρ分別為電離層延遲與對流層延遲，單位為m;ερ為其他誤差的綜合項，單位為m。

進行PVT(position velocity and time)解算時，需采用衛星信噪比cn0確定觀測噪聲序列的方差-協方差陣Rk，具體為

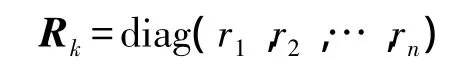
式中，ri取值為

上式中相關參數為經驗參數，與模塊相關。

三、測試與分析

1.測 試

為測試算法的正確性，對PVT定位程序進行了路測，部分測試環境如圖1所示。

圖1 測試環境

測試天線使用普通的導航天線，模塊為u-blox LEA-6T模塊(設置測試采樣率為1 s，實際測試過程中也使用了其他模塊，效果一樣)，測試方法如下:

1)設備安置。將導航天線固定于測試車車頂并連接至模塊的天線輸入端，同時使用數據線連接模塊和計算機，使得模塊的實時觀測數據可以流入計算機并交給PVT程序。

2)模塊設置。為模塊通電，通過模塊的控制軟件U-Center對模塊的工作方式、數據輸出等進行設置，并保存。

3)開始測試。啟動PVT程序，進行實時PVT解算。

為形成參照，分析PVT定位程序的解算精度，在測試車車頂的導航天線旁邊安置Trimble R10便攜接收機，該接收機連接湖北省連續運行參考站系統(HBCORS)，工作模式為RTK。

2.對比分析

為說明本算法相比偽距單點定位精度有很大改善，在事后進行了偽距單點定位解算，這樣加上實時解算的結果，就獲得了3組數據:

1)PVT定位程序實時解算結果。

2)Trimble R10的實時RTK解算結果。

3)事后偽距單點定位解算結果。

眾所周知，RTK固定解精度很高，因此在進行偽距PVT解算精度分析過程中，以同步的RTK固定解為參考值，比較PVT定位程序實時解算結果與事后偽距單點定位解算結果相對同步RTK固定解在水平、豎直方向的偏差(如圖2、圖3所示)。

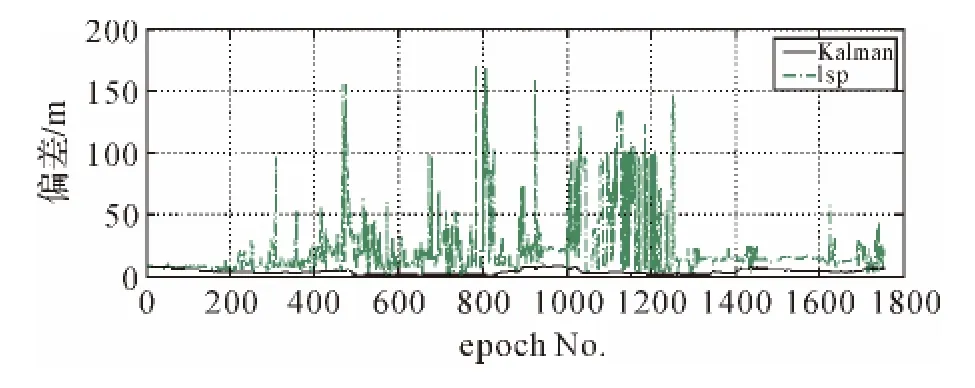
圖2 最小二乘與卡爾曼濾波對比(水平方向)

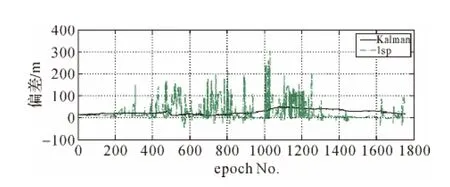
圖3 最小二乘與卡爾曼濾波對比(豎直方向)

比較圖2與圖3可見，改進的動態卡爾曼濾波算法相比最小二乘算法，不論是水平方向還是豎直方向，定位效果都提高很多。

為便于定量分析，給出實時解算結果與事后最小二乘解算結果在各個誤差段的統計信息，由于關注的是平面位置，下面僅給出水平方向上的誤差統計(見表1)。

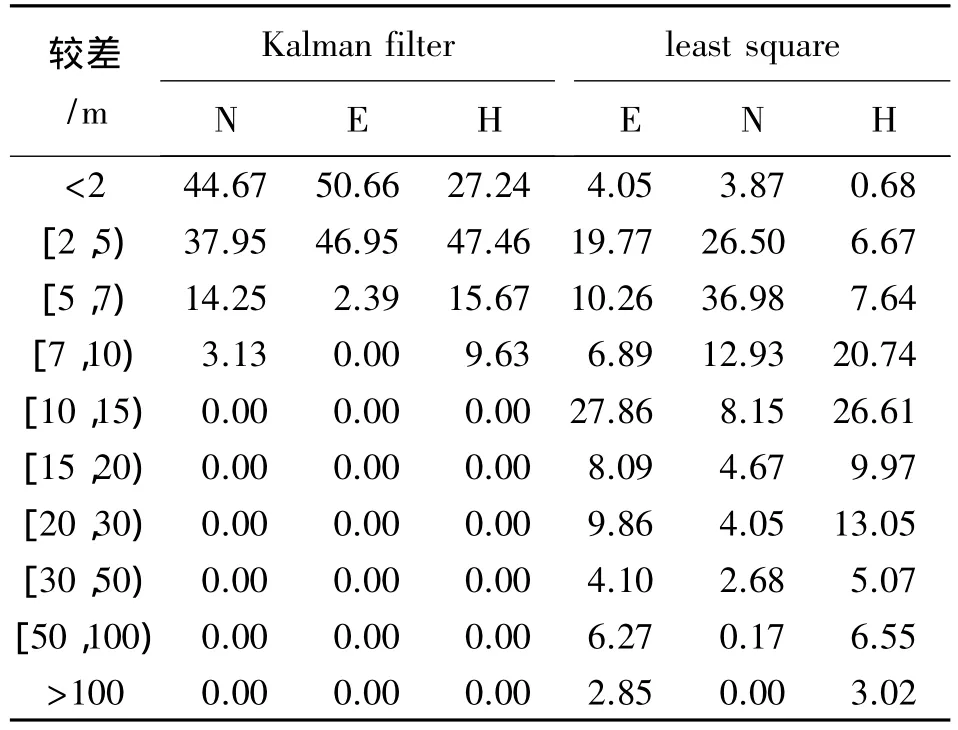
表1 最小二乘與卡爾曼濾波解算結果誤差統計(%)

從表1可見，優化的實時卡爾曼濾波算法超過70%歷元水平精度優于5 m，所有定位結果水平精度均優于10 m;而最小二乘算法中，水平精度優于5 m的歷元不到10%，多數歷元水平精度介于7～30 m(70%)。相比最小二乘算法，優化的實時卡爾曼濾波算法解算精度提高很多。

四、結束語

本文研究了在城市道路下使用低成本導航天線與電子消費類GPS模塊進行實時動態定位的方法，算法中僅使用單頻偽距和多普勒觀測值，對系統成本要求不高。算法以動態卡爾曼濾波為基礎，加上基于衛星信噪比的觀測序列噪聲方差-協方差陣自適應確定方法，克服了復雜環境下GPS定位效果差的缺點。相比最小二乘算法，本算法定位效果有很大提高，通過實時解算測試說明，在城市街區，超過70%歷元水平精度優于5 m，所有歷元水平精度優于10 m。

［1］秦永元.卡爾曼濾波與組合導航原理［M］.西安:西北工業大學出版社，1999:2-3.

［2］GELB A.Applied Optimal Estimation［M］.Cambridge:MIT Press，2001:72-74.

［3］蔡艷輝，程鵬飛，李夕銀.用卡爾曼濾波進行GPS動態定位［J］.測繪通報，2006(7):6-8.

［4］董緒榮，陶大欣.一個快速Kalman濾波方法及其在GPS動態數據處理中的應用［J］.測繪學報，1997，26(3):221-227.

［5］JWO D J，WANG S H.Adaptive Fuzzy Strong Tracking Extended Kalman Filtering for GPS Navigation［J］.IEEE Sensors Journal，2007，7(5):778-789.

［6］MISRA P，ENGE P.Global Positioning System:Signals，Measurements，and Performance［M］.2nd ed.Massachusetts:Ganga-Jamuna Press，2006:200.

［7］宋迎春，朱建軍，陳正陽.動態定位中測量噪聲時間相關的 Kalman濾波［J］.測繪學報，2006，35(4):328-332.

［8］龔真春，陳安寧，李平，等.GPS動態定位中自適應卡爾曼濾波方法的應用研究［J］.測繪通報，2006(7):9-12.

［9］單瑞，趙鐵虎，于得水，等.單點GPS多普勒測速模型比較與精度分析［J］.測繪通報，2013(3):7-10.

［10］趙玉鳳，徐建華，何文濤，等.一種利用多普勒頻移平滑偽距的方法:中國，101865992A［P］.2010-10-20.