三角形在位勢下一維無限深勢阱中粒子的量子特性研究
向少華,賴青青,陳英
(懷化學院電氣與信息工程學院,湖南懷化418008)
三角形在位勢下一維無限深勢阱中粒子的量子特性研究
向少華,賴青青,陳英
(懷化學院電氣與信息工程學院,湖南懷化418008)
利用有限差分方法數值求解了具有三角形在位勢的一維無限深勢阱中粒子的運動學方程,討論了在位勢對粒子幾個最低能量本征值和與其對應的概率密度分布函數的影響.結果表明:粒子的最低能量隨在位勢強度的增加而增大,而它們的概率密度分布函數則呈現各不相同的空間特性.基態概率密度分布函數的波峰朝左移動,第一激發態的波峰朝右移動,而第二激發態的兩側波峰被削弱,中心峰被增強.
量子力學;無限深勢阱;三角形在位勢;有限差分法
在量子力學的建立過程中,一維無限深勢阱模型是最簡單但又最重要的量子體系.該體系的理論成果為我們展示了量子力學在描述微觀粒子行為上要比經典物理更精確、更準確和更高級.長期以來,人們圍繞該模型定態薛定諤方程求解以及邊界條件等問題進行了廣泛而深入的研究.在勢函數較為簡單的量子體系中,通常是直接求解這個二階偏微分方程,或者在能量算符表象下,將薛定諤方程轉化為哈密頓算符的本征方程,求出它的本征值和本征函數,按能量本征函數展開所求波函數[1].但對于復雜的勢函數,量子體系薛定諤方程的求解十分困難,得不到解析解.一般采取數值計算方法討論這些復雜量子體系的量子特性.在這些近似處理方法中,有限差分方法是簡便而有效的方法之一.該方法已被人們運用到一維無限深勢阱模型[2,3],一維線性諧振子模型[4,5]和氫原子體系[6]等.本文將利用有限差分方法研究一類新穎的一維無限深勢阱模型,即微觀粒子囚禁在一個無限深勢阱中且勢阱底部還有一個三角形勢場的作用.我們討論的模型具有一定的理論指導意義.因為在實際金屬中,電子并非是自由的,它們還受到金屬中雜質、缺陷和晶格振動等的影響,使電子處在有勢函數漲落的阱底運動[7].
1 具有三角形在位勢的一維無限深勢阱模型的理論描述
無在位勢的一維無限深勢阱模型(或稱為經典無限深勢阱模型)中,微觀粒子的運動遵循薛定諤方程

式中u是粒子的質量,E為粒子的能量本征值,Ψ(x)是與之對應的能量本征函數,U(x)為勢阱函數,其形式為
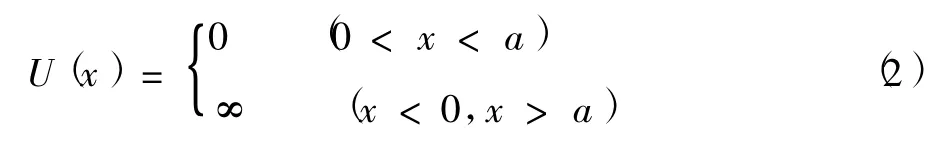
上式中a為勢阱寬度.假設粒子的能量滿足0<E<V0并根據波函數標準化條件,不難得到粒子的能量本征值為

和對應的本征函數是
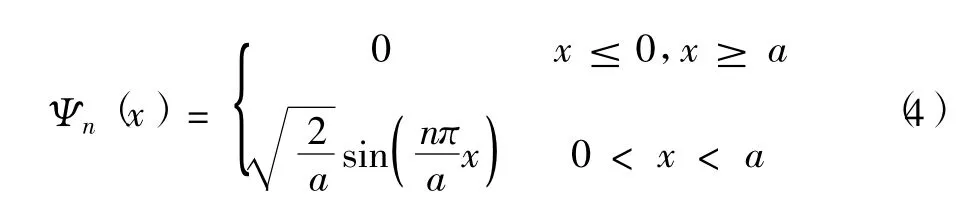
由此看出:與經典粒子不一樣,在無限深勢阱中,粒子的能量是分立,不是連續的;n=1時能量最小,叫基態能量(E1≠0)或零點能,n=2為第一激發態,n=3為第二激發態,其它的依此類推.因此,粒子在無限深勢阱中運動表現為量子化效應.
無在位勢的無限深勢阱模型是量子力學中僅有的幾個可以精確求解的理論模型.在上面的例子中,勢阱底部勢函數為零,即為平坦的.在本文中我們討論一類特別的理論模型,其阱底部勢函數如圖1所示,稱為三角形在位勢.由于它的作用,使定態薛定諤方程成為一個變系數的二階偏微分方程,求解異常繁瑣與困難,故我們采取有限差分方法研究粒子的能量本征值和本征函數,進而討論概率密度分布函數.
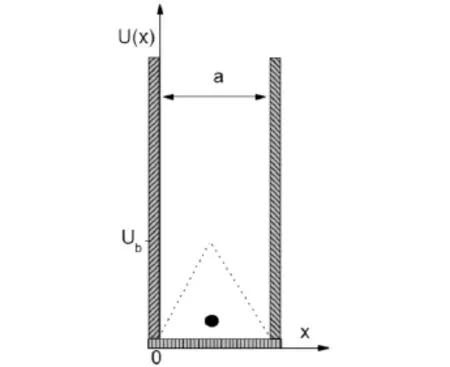
圖1 具有三角形在位勢的一維無限深勢阱模型
在利用有限差分方法處理薛定諤方程時,我們將粒子的波函數和哈密頓能量算符作如下變換

這樣偏微分方程就轉化為矩陣方程,即轉化為
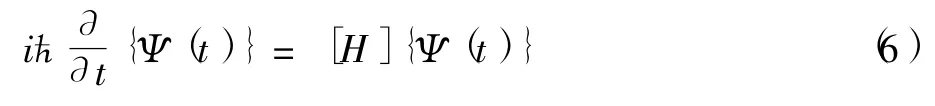
同時將勢阱空間無限劃分,切割成N個空間格點,格點間的晶格常數為Δx=b,于是我們用列矢量{Ψ(x1),Ψ(x2),…,Ψ(xN)}T表示粒子在時間t的波函數Ψ(x,t).
接下來求哈密頓算符

的矩陣形式.根據有限差分方法,我們將波函數對空間坐標的二階微分用下式代替
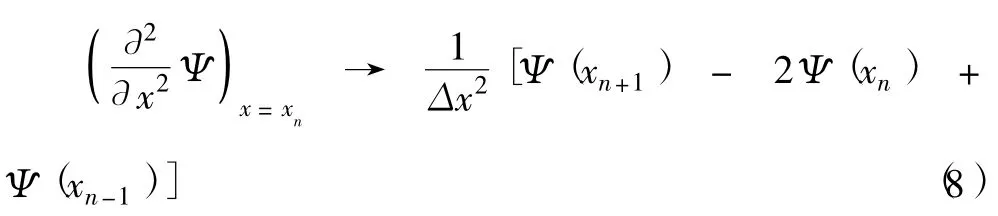
和
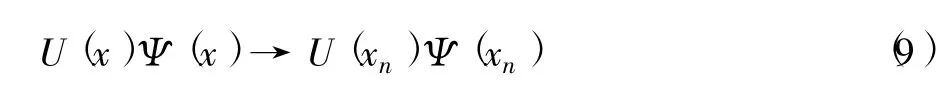
從而有:
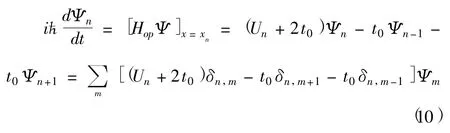
這里與格點坐標相關的物理量省略了對應的坐標,而用編號代替,如Ψ(xn)用Ψn表示,U(xn)用Un表示,等等,t0=?2/2ub,δn,m為克羅內克符號.
由方程(10)可知,哈密頓量算符的矩陣元是
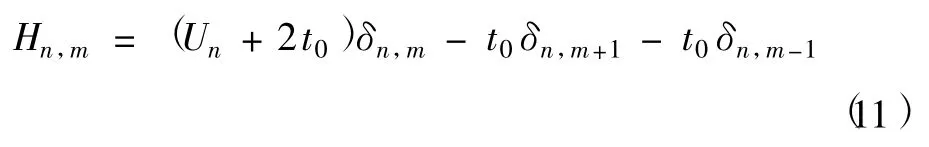
因此,一旦對勢阱寬度劃分確定后,我們就可以寫出哈密頓矩陣,其表達式是

假設哈密頓矩陣(12)的本征值為Eα,與其相對應的本征矢為{α},則哈密頓量矩陣方程的解是
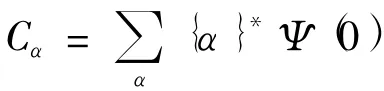
2 粒子能量本征值和概率密度分布函數分析與討論
根據前面的理論知識,我們借助于Matlab軟件數值計算粒子在具有三角形在位勢的一維無限深勢阱中的能量本征值和概率密度分布函數.在數值計算中我們設勢阱寬度為120 nm,勢阱區域劃分為120個格點數,三角形在位勢的數學表達式假設為
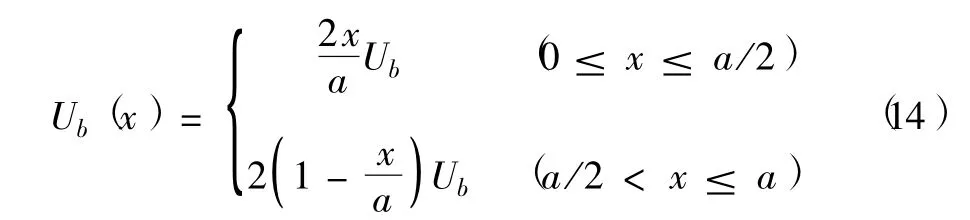
式中Ub為在位勢強度,模擬中其單位為eV.
表1是在各種三角形在位勢作用下粒子前四個能量本征值,其中Ub=0為經典的無限深勢阱的情況.

表1 三角形在位勢作用下粒子的前四個最低能量值
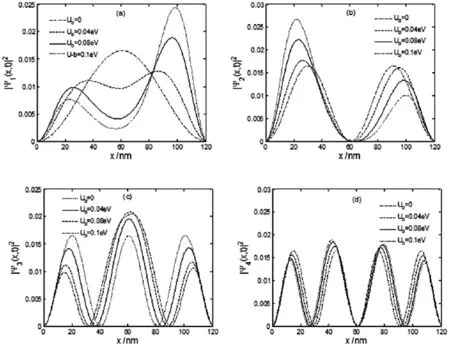
圖2 不同三角形在位勢下粒子前四個概率密度分布函數
從表1中可以看處,在三角形在位勢的作用下,粒子的最低幾個能級的能量將會增加.這種增加可以根據量子力學基本原理得到解答.眾所周知,粒子的能量等于動能與勢能之和,即:E=p2/2u+U(x),因此,在位勢的作用相當于給粒子施加了一作用力,使粒子的能量發生改變.在本例子中,我們的在位勢始終為正,故而能量增加,能級向上移動.同時,我們從圖2中發現:在在位勢的作用下,各級能量本征值的概率密度分布函數不再是正弦變化,展現出了豐富、有趣的物理信息.對于基態和第一激發態概率密度分布函數,隨著在位勢的增加,它們不再是對稱分布的,它們的波峰將發生漂移.基態概率分布函數的波峰朝右移動,而第一激發態的波峰朝左移動,第二激發態概率密度分布函數的中心波峰振幅被增強,而兩側的波峰被削弱.這些結果也表明在在位勢的作用下,粒子的宇稱遭到了破壞.我們知道,在經典的無限深勢阱模型中,由于勢阱函數有U(x)=U(-x),則量子系統具有確定的宇稱.但粒子在三角形在位勢的驅動下,勢阱函數U(x)=U(-x)不再成立,因而,該囚禁粒子系統沒有明確的宇稱,波函數表現為非奇非偶.此外,我們由圖2可以推知,施加的在位勢不改變波函數波節的個數,卻改變了波函數節點(波函數為零的地方)出現的位置.正如文獻[8]所述,有限差分法計算得到的結果只在最低幾個能量值與解析結果相一致,而在高能態情況,它們偏離很大.這種差異主要是有限差分法只考慮到二階項,忽略了三階以上的項.因此,對于高階能量本征值和本征函數情況則需采用其它的近似處理方法.
3 結論
本文采用有限差分方法和Matlab數學軟件,數值計算了粒子在一維無限深勢阱且阱底有一個三角形在位勢的模型中幾個最低能量本征值和相應的概率密度分布函數.結果表明施加的在位勢對粒子本征值能量及本征函數有顯著的影響.與經典無限深勢阱模型相比,盡管在位勢不改變粒子波函數節點個數,但使節點出現的位置坐標發生了移動,更使概率密度分布函數呈現出了空間分布的非對稱性.這些有趣的現象對全面認識無限深勢阱模型和深刻理解量子力學基本知識與原理有極大的幫助.我們處理的思路為其它類型無限深勢阱模型的求解及非經典特性研究提供有價值的理論基礎.
[1]P.A.M.Dirac.The Principles of Quantum Mechanics[M].4thed.,Oxford University Press,1958.
[2]劉曉軍.有限差分法解薛定諤方程與Matlab實現[J].高師理科學刊,2013(3):68-70.
[3]朱蕭霄,崔艷波,丁鑫,等.有限差分法解薛定諤方程及其應用[J].常州工學院學報,2014(4):37-41.
[4]劉建軍,翟利學.有限差分法解能量本征值方程[J].北京工業大學學報,2008(3):325-331.
[5]宮建平.有限差分法求解薛定諤方程[J].晉中學院學報,2014(3):1-6.
[6]陳皓,高明,汪青杰.用有限差分法解薛定諤方程[J].沈陽航空工業學院學報,2005(1):87-88.
[7]黃昆,韓汝琦.固體物理學[M].高等教育出版社,1999.
[8]S.Datta.Quantum Transport:Atom to Transistor[M].Cambridge University Press,2005.
Research on Quantum Properties of Particle Trapped in One-Dimensional Infinite PotentialWellwith Triangular On-Site Potential
XIANG Shao-hua,LAIQing-qing,CHEN Ying
(College of Electrical and Information Engineering,Huaihua University,Huaihua,Hunan 418008)
The equation ofmotion for wave function of a particle trapped in one-dimensional infinite potential well with a triangular on-site potential is solved numerically bymeans of the finite differencemethod.The effect of the on-site potential on the first few energy levels and the corresponding probability densities is discussed.It is shown that theminimum energies of the particle increasewith the increasing of the on-site potential,whereas their probabilitiesare completely different from each other in the spatial distribution.When increasing the on-site potential,the wave crest of the ground state probability density canmove to the left and that of the first excited state willmove to the opposite direction.For the second excited state,the increase of the centralwave-crest amplitude is observed and on the contrary,the wave crests in both sides are suppressed.
quantum mechanics;infinite potentialwell;triangular on-site potential;finite differencemethod
O413.1
A
1671-9743(2015)11-0035-04
2015-05-30
湖南省教育廳教改項目“基于創新素質培養為目標的物理學專業課程體系的構建與實踐研究”(湘教通[2012]401號);懷化學院教改課題“基于創新素質培養為目標的物理學專業課程體系的構建與實踐研究”(201202).
向少華,1972年生,男,湖南麻陽人,教授,博士,研究方向:物理學教學與科研.

