期權定價方程的緊致差分算法
黃振平
(長沙理工大學數學與計算科學學院,湖南長沙410004)
期權定價方程的緊致差分算法
黃振平
(長沙理工大學數學與計算科學學院,湖南長沙410004)
利用緊致有限差分方法進行空間離散,修正龍格庫塔方法進行時間離散,建立一種求解期權定價方程的數值格式,較好地解決了對空間與時間混合導數項的離散問題,并在空間和時間上都保持了較高階精度.所得數值結果證實了該數值格式具有較高的精度.
緊致有限差分方法;修正龍格庫塔方法;期權定價方程;數值解
引言
期權定價領域的開創性工作是由Black和Scholes在1973年中,在通過求解一個拋物型歐式期權偏微分方程(俗稱Black-Scholes方程)時發現的.該模型在學術界引起強烈反響,對投資者如何對期權定價和風險對沖都產生了重大影響,并且對之后的衍生工具發展起到了決定性的作用.
目前已經有各種有限差分方法[1]研究了Black-Scholes方程.有限差分法的一個主要缺點是隨著逼近階的增加,計算量也相應擴大.1992年,Lele總結Pade格式[2],得到了任意高階精度對稱緊致有限差分格式的推導方法,高階緊致有限差分法考慮的是函數值和它的在每個離散點處未知的一階二階導數.對比有限差分格式,該方法,在相同網格點下,可以給出更高的精度和解的特性,此特性使他們更接近光譜方法,例如使用五個節點即可達到六階精度[3].該方法的應用十分廣泛,曾經被用來研究彈性波方程、泊松方程、N-S方程等.
本文利用緊致有限差分方法進行空間離散,修正Runge-Kutt方法進行時間離散,建立一種求解期權定價方程的數值格式,較好地解決了對空間與時間混合導數項的離散問題,并在空間和時間上都保持了高階精度.所得數值結果證實了該數值格式具有較高的精度.
1 緊致差分方法介紹
緊致有限差分方法是使用函數值的某種線性組合來表示該函數導數值的線性組合的一類差分方法,該方法增加了差分格式的精度與穩定性.
1.1 空間離散,構造三點六階精度緊致差分格式[3]:
對于區間[a,b]上的函數f(x),考慮節點為x0,x1,…,xN的均勻網格,步長h=xi+1-xi,i=0,1,…,N-1.節點處的函數值為vi,一階和二階導數值分別為v′i和v″i.現在開始構造均勻網格上的三格點六階精度緊致差分格式.
文獻[4]中,作者采用特殊緊致差分格式來推導二階導數:用三個連續點處的函數值和它的一階導數值來近似位于同樣三點處的二階導數值,該二階導數值具有六階精度.借用這個想法,我們得出以下混合問題的六階差分格式,具體的推導過程可參照文獻[5].
對于內點,二階導數值與函數值之間滿足關系:
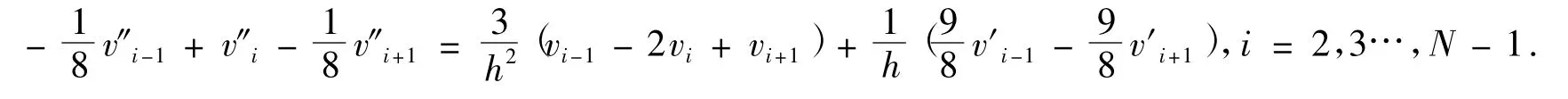
對于邊界點處的二階導數構造如下格式:
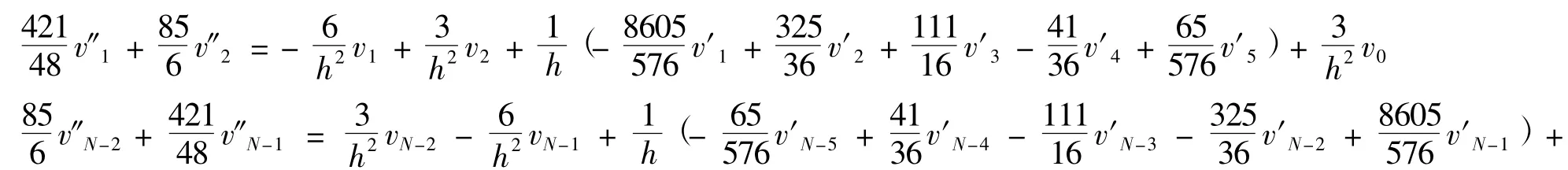
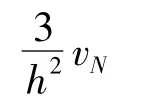
聯合上面三式,寫成矩陣形式:
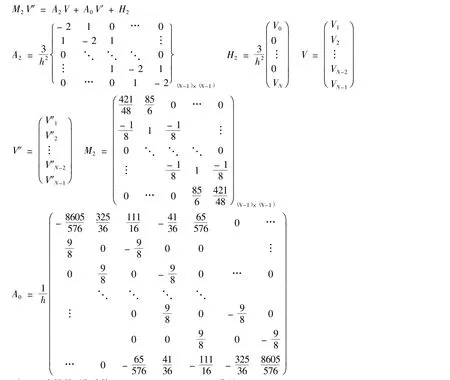
對于一階導數,設系數ai-1,ai,ai+1,mi-1,mi+1滿足:
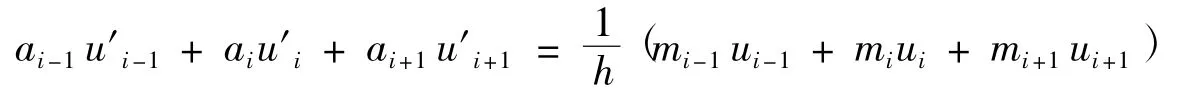
將上式兩端分別在xi點進行Taylor展開,結合六階精度,得到系數線性方程組,解之,得如下三點六階緊致格式,具體推導可以參考[5].
對于內點xi,一階導數值與函數值之間滿足關系:
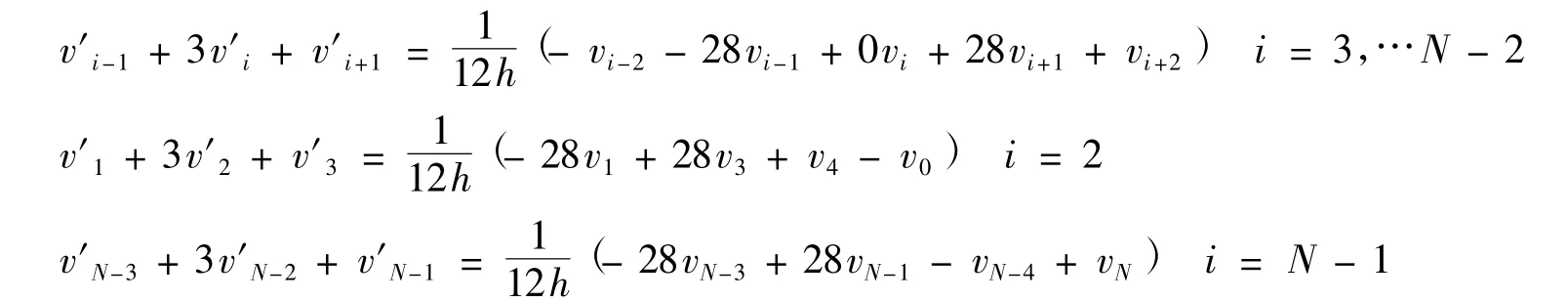
對于邊界點處的一階導數構造如下格式:
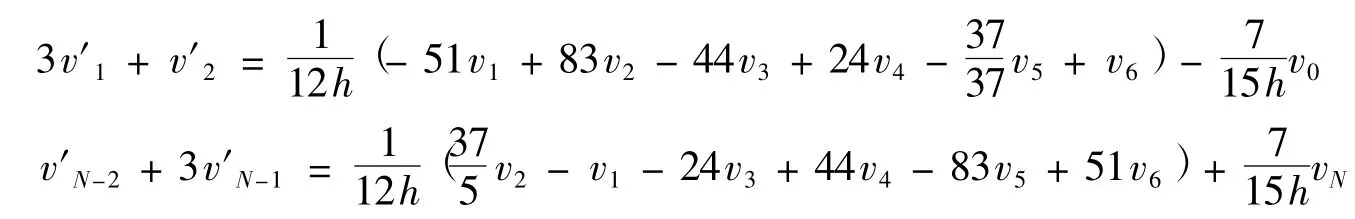
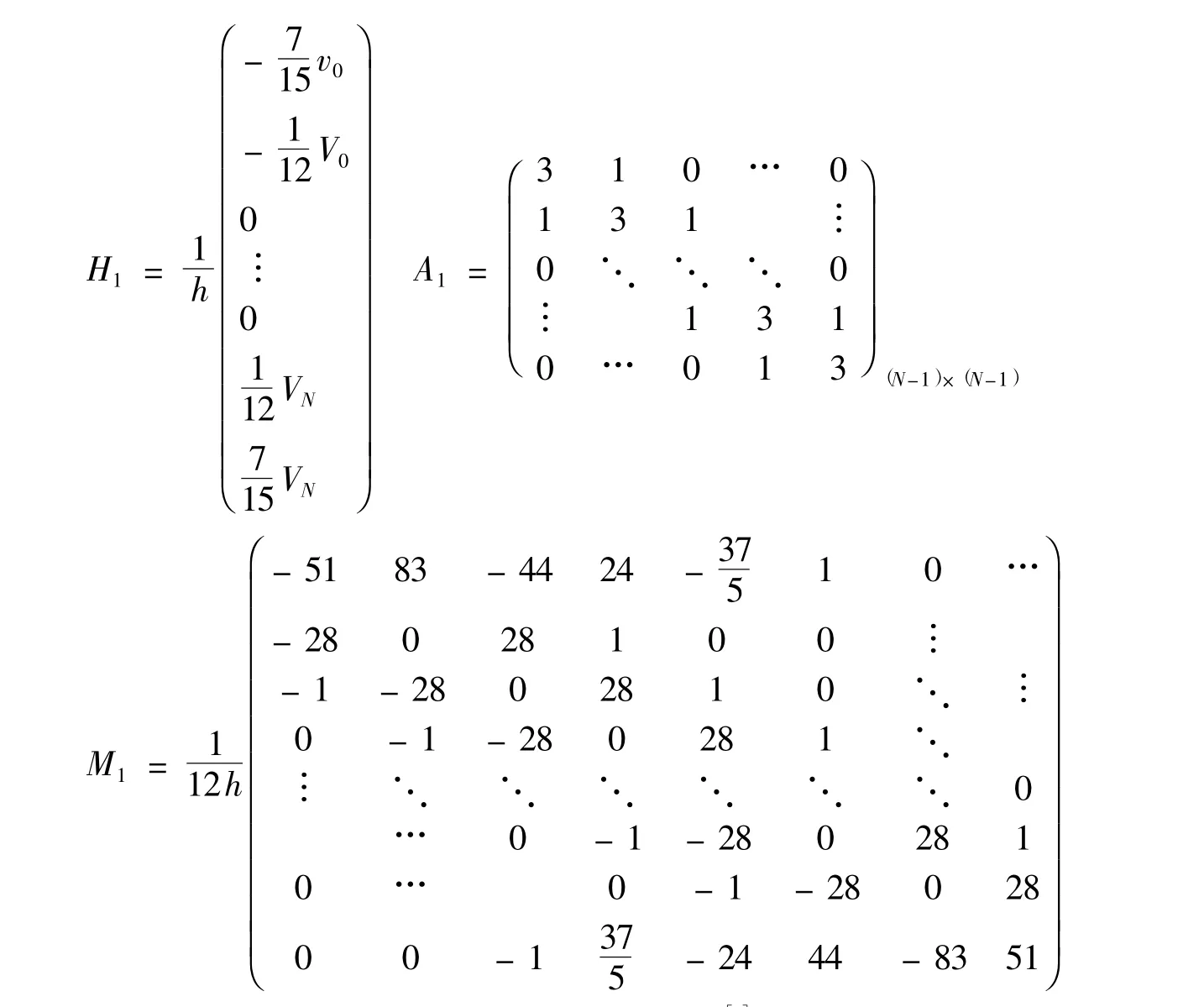
將上述五式寫成矩陣形式:A1V′=M1V+H1
1.2 時間離散,使用修正Runge-Kutta方法[6]:
為了提高計算效率,減少內存的占用,本文使用了同樣具有4階精度的修正Runge-Kutta格式.
修正Runge-Kutta格式顯式推進計算公式如下:
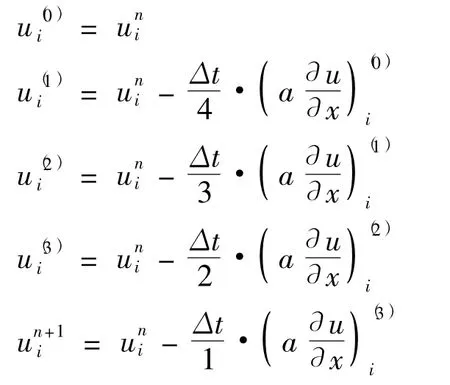
四步時間推進使得4階修正Runge-Kutt.格式具有4階精度,格式具有較高的穩定性,使得顯式時間推進能夠取到較大的時間步長,加快計算收斂的速度.
2 緊致差分算法解期權定價方程
用v(s,t)表示期權價格,則歐式看漲期權模型滿足如下Black-Scholes方程
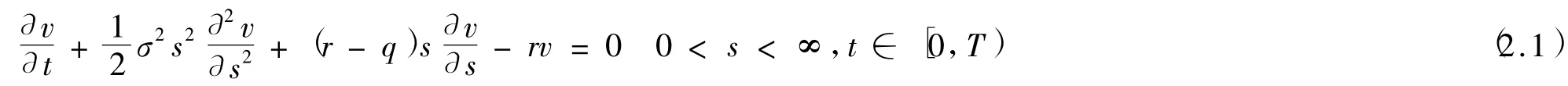
初值條件

邊界條件
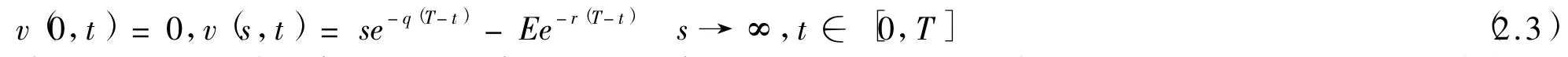
其中:是R無風險利率,q是紅利率,σ是波動率,T是到期日,E是敲定價格,方程(2.1)是一個變系數倒向拋物型方程,(2.1)—(2.3)是一個倒向定解問題.
做變換

可以將歐式期權模型(2.1)—(2.3)轉化為常系數對流擴散方程的定解問題
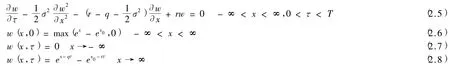
其中x0=ln E
為了習慣方便,下面以u(x,t)表示期權價格,t=τ.下面是用緊致的差分方法,通過matlab來求解方程(2.5).
等距網格剖分:
對于空間變量x,計算區域取為有限區域Ω=(xmin,xmax).空間和時間網格節點分別為Ωh={xi=xmin+(i-1)h,i=1,2,…,M+1,h=(xmax-xmin)/M}
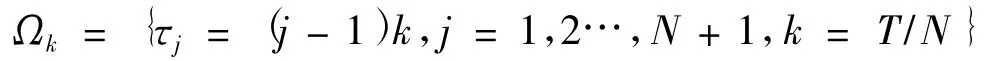
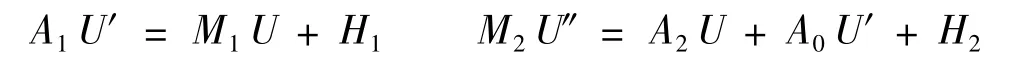
若知道u在x=xi,i=2,…,M處的值,通過matlab軟件,由雅可比迭代可以求得對應各節點處的一階和二階導數值
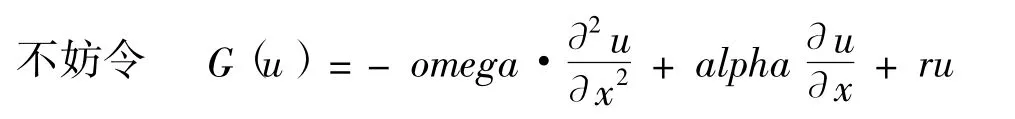
則x=xi,i=2,…,M,t=tn時,由修正Runge-Kutt方法得:
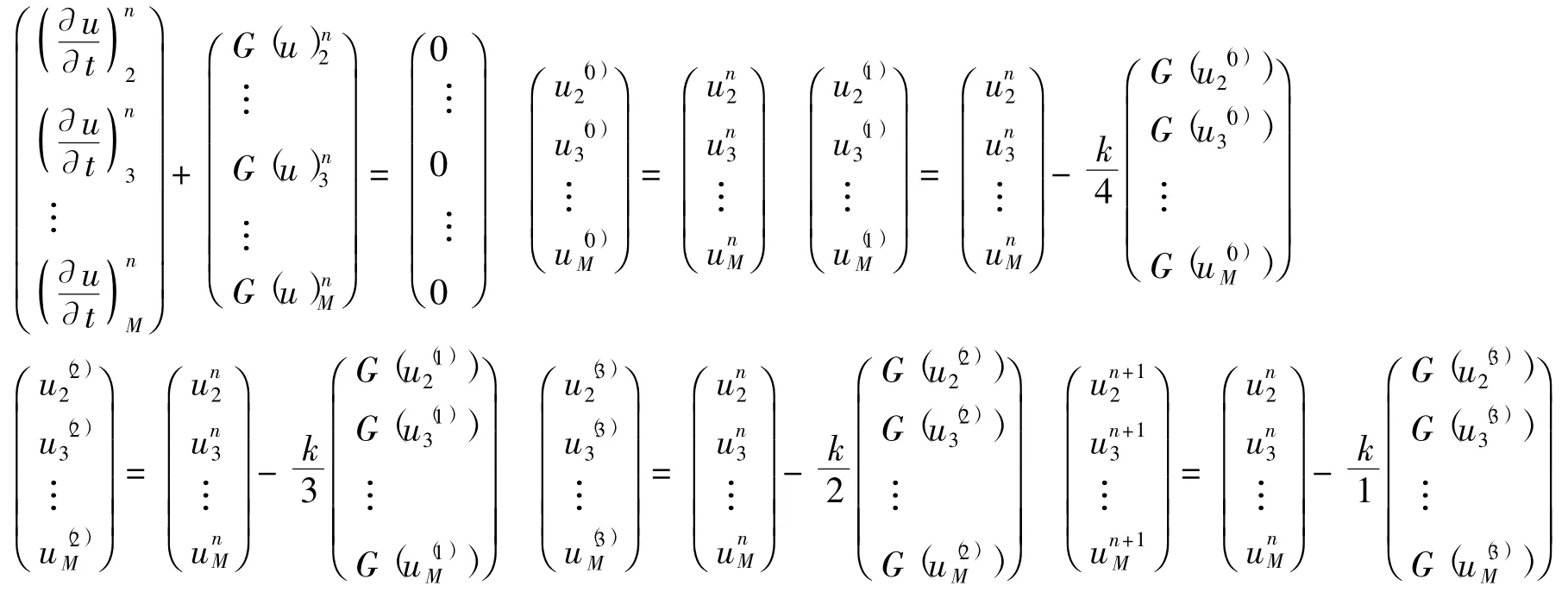
于是結合初邊值和第n層的一階,二階導數,由第n層u的函數值可推出第n+1層的函數值,不斷迭代,繼而求出t=T層的函數值.
具體方法詳見篇尾的matalab程序代碼.
3 數值實驗
這一節中,我們通過MATLAB,利用緊差分格式進行數值試驗,表中e1表示T時刻精確解和數值解的誤差,分別表示e1在T時刻的誤差二范數和無窮范數.對空間變量x,M等分后步長為h,對時間變量t,N等分后步長為k.下圖橫坐標為In(x),縱坐標為log10|e1|,x1為左端點,x2為右端點.
算例1:參數取值是:r=0.05,q=0.2,σ=0.3,E=2,T=0.25,N=1600.
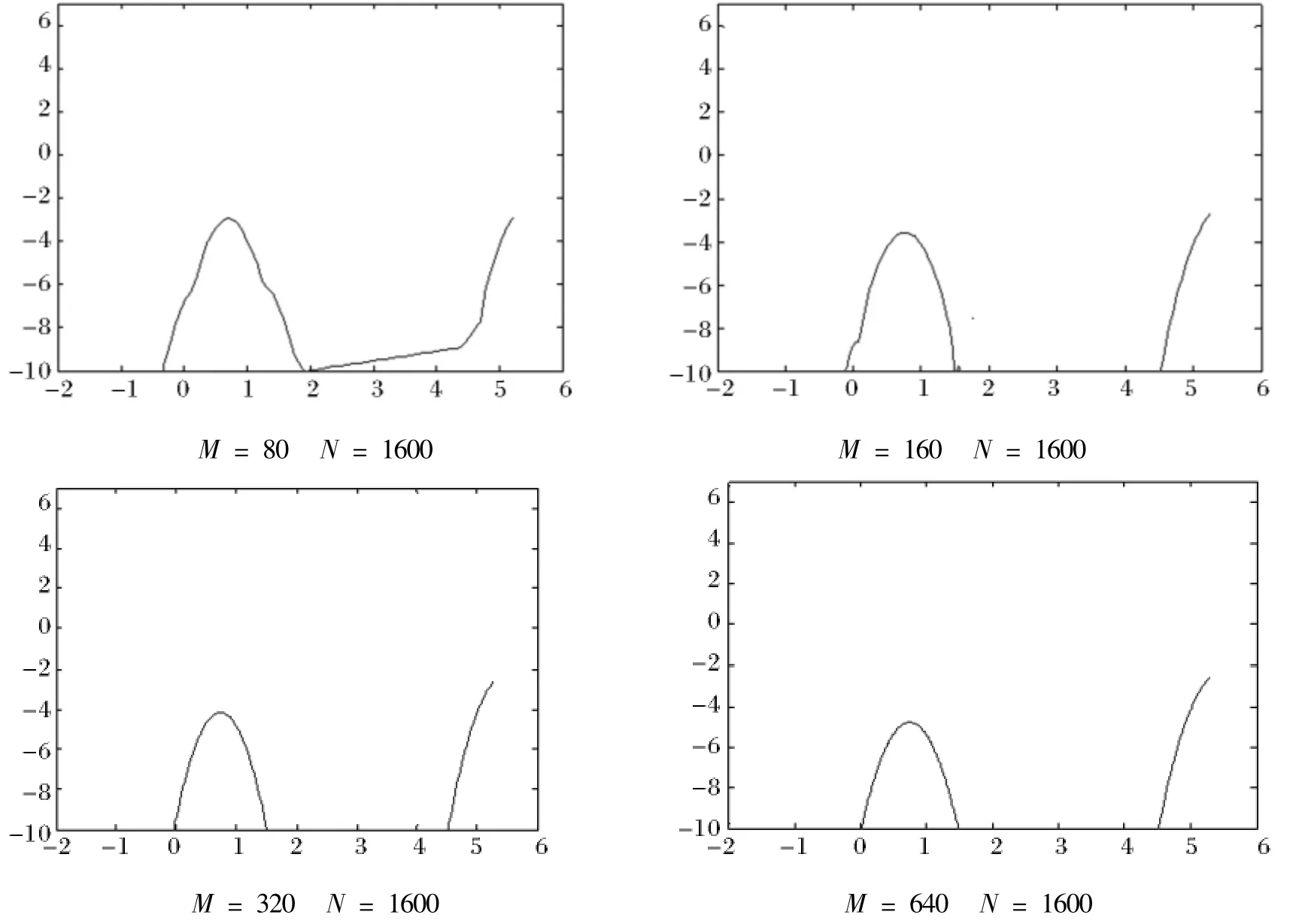
算例2:參數取值是:r=0.05,q=0.2,σ=0.3,E=2,T=0.25,N=1600,M=160
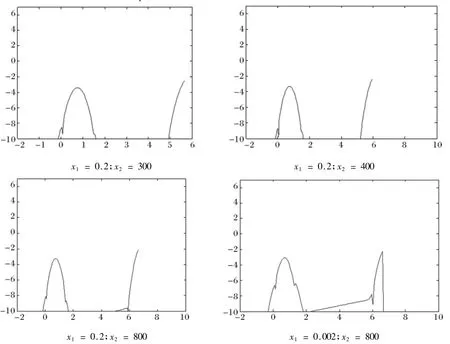
算例3:r=0.05,q=0.2,σ=0.3,E=2,N=1600,M=160,s1=0.2,s2=400

表1 緊致差分格式的誤差范數
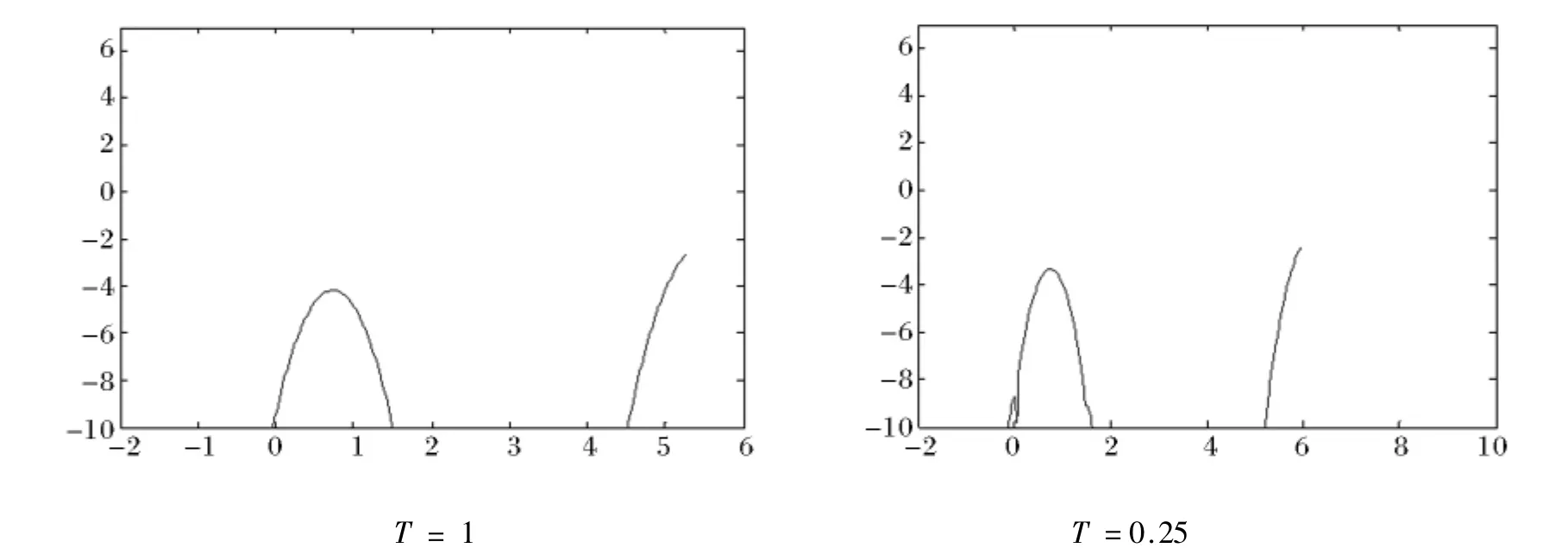
綜上述,邊界處誤差比較大,可能源于該格式邊節點處精度略有下降有關,但經過實驗數據對比,整體上該方法是穩定可行的,接下來將會繼續改進.
[1]劉銘輝.歐式看漲期權定價微分方程的有限差分求解方法[M].哈爾濱:哈爾濱工業大學,2012:11-18.
[2]LELE SK.compact finite difference schemes with spectral-like resolution[J].Journal of computationnal Physics,1992(103):16-42.
[3]Jichao Zhao.Highly accurate compactmixedmethods for two pointboundary value problems[J].elsevier,2006(188):1402-1417.
[4]P.C.Chu,C.Fan,A three-point combined compact difference scheme,J.Comput.Phys,1998(140);370-399.
[5]Shukla,R.K.,!Zhong,X.:Derivation of high-order compact finite difference schemes for nonuniform grid using polynomial interpolation.J.Comput.Phys,2005(204):404-429.
[6]沈露予.不可壓縮Navier-Stokes方程高精度算法研究[D].南京:南京信息工程大學,2005:8-100.
Compact Difference Algorithm for the Option Pricing Equation
HUANG Zhen-ping
(Changsha University of Science and Technology,Changsha,Hunan 410004)
Acompact difference scheme is established for solving the option pricing equation by using the the compact finite differencemethod in space discretization and themodified Runge-Kuttamethod in time discretization.Themixed derivative is skillfully treated and the high order accuracy ismaintained both in space and time.It is confirmed that the numerical schemes obtained from the scheme have high accuracy.
compact finite difference method;modified Runge Kutta method;option pricing equation;numerical solution
O155
A
1671-9743(2015)11-0018-06
2015-10-21
黃振平,1985年生,男,湖南郴州人,碩士研究生,研究方向:偏微分方程數值解.

