基于磁流變彈性體變剛度動力吸振器的研究

宋偉志，周 輝，趙艷青，趙海軍，姚永玉

(1.洛陽理工學院 機械系，河南 洛陽471000;2.淮陰工學院，江蘇 淮安223001)

0 引 言

對于工程結構、建筑橋梁以及機械系統等進行有效的減振十分必要。動力吸振器始于1902年，由Frahm 發明［1］。因為其結構、性能及經濟等方面的優勢而得到了廣泛研究。但傳統動力吸振器由于結構參數固定，只有當固有頻率等于外界激振頻率時，才可對主系統進行有效減振［2］，對于變頻激振，其減振性能會大幅降低，嚴重制約了吸振器的使用范圍。

近些年自適應動力吸振器［3－7］由于結構簡單，性能穩定，且可以有效拓寬吸振器減振頻帶而得到快速發展。磁流變彈性體 (Magnetorheological elastomers，MRE)作為一種新型智能材料，兼備磁流變材料及彈性體的性能，同時克服了磁流變液易發生沉降的問題［8］。本文以MRE為彈性元件，設計并研究了基于磁流變彈性體［9］的變剛度動力吸振器。通過理論仿真和實驗研究證明，該吸振器通過調節自身剛度，其減振頻帶可達到5 Hz。當外界激振頻率在一定范圍發生變化時，吸振器通過追蹤外界激振頻率，充分發揮其減振性能，對主系統的振動抑制有大幅度提高。

1 基于MRE 變剛度動力吸振器的原理分析

現階段對于MRE 磁流變效應的分析基于磁偶極子理論［10］。即MRE 中的勵磁性顆粒在磁場作用下磁化而彼此產生相互作用力，由于相互作用力的不同導致模量不同。目前MRE的工作模式主要有擠壓式和剪切式，鑒于剪切式的磁流變效應較為明顯，本文采用剪切式設計結構，基于MRE的吸振器實物如圖1所示。高導磁支架、MRE 及吸振器的振子組成閉合磁回路，勵磁線圈在電流作用下產生磁場并穿過MRE。

圖1 磁流變彈性體動力吸振器Fig.1 DVA based on MRE

MRE 剪切剛度計算如式(1):

式中:k為彈性體剛度;G為彈性體有效剪切模量，其值等于外界不加磁場時的剪切模量G0加上磁場作用下模量變化量ΔG［11］，如式(2)所示;A為彈性體的有效剪切面積;h為彈性體的厚。

根據吸振器固有角頻率和本身剛度及質量的關系:

式中:ω為吸振器的固有角頻率;k為吸振器彈性元件剛度;m為吸振器振子質量，可知:

根據MRE 剛度與剪切模量的關系及吸振器固有頻率與剛度之間的關系易知，可通過改變勵磁線圈電流的大小改變穿過MRE的磁場，進而對吸振器的固有頻率進行調節，使之等于外界激振頻率，充分發揮吸振器的減振性能，實現寬頻減振的目的。設吸振器最小剛度(即不加電流時)為kmin，電流最大時，達到磁流變彈性體磁飽和，設其剛度增加為Δk，則吸振器的有效減振頻帶為，這就是基于磁流變彈性體動力吸振器拓寬減振頻帶的基本原理。

2 變剛度動力吸振器的仿真研究

可將主系統和吸振器簡化為二自由度振動系統，其模型如圖2所示。

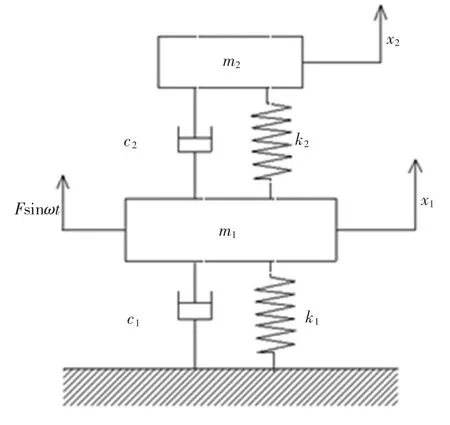
圖2 主系統—吸振器模型Fig.2 The model of primary system and DVA

由以上模型建立運動學方程如下:

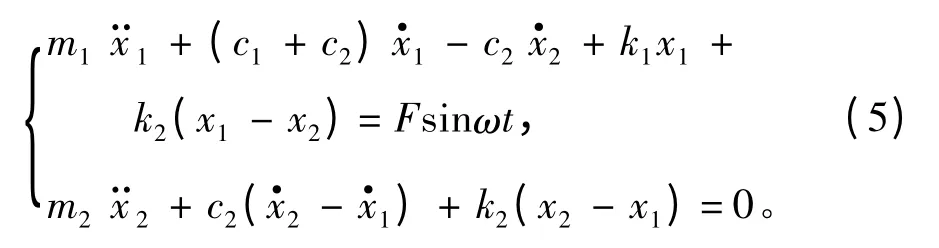
利用上述運動學方程建立模型并進行仿真研究，系統采用結構參數如表1所示。

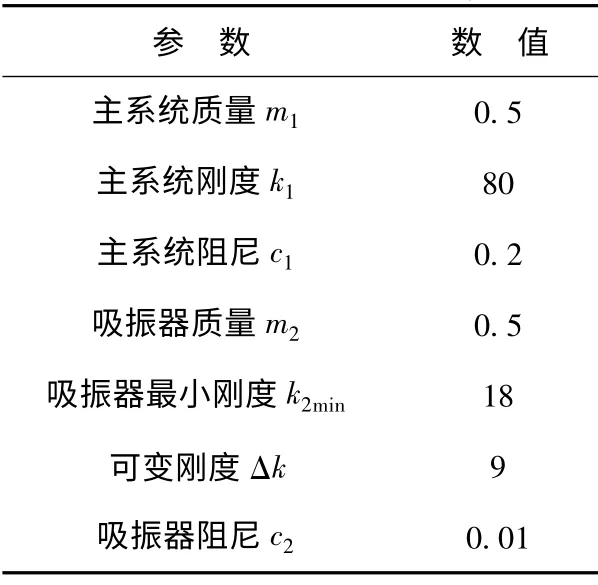
表1 系統結構參數Tab.1 Parameters of the system

利用Matlab/Simulink 模塊建立仿真模型，做出主系統的幅頻特性曲線，如圖3所示。

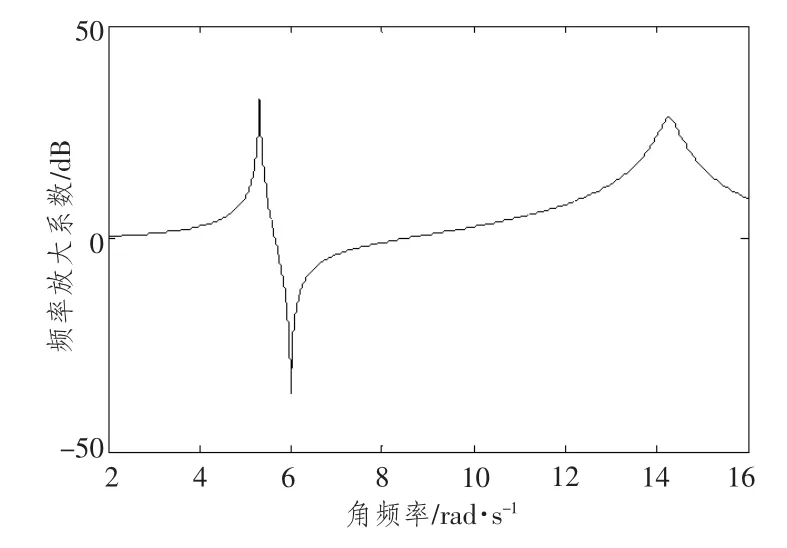
圖3 主系統幅頻特性曲線Fig.3 Amplitude-versus-frequency curve of primary system

由圖3 可知，當外界激振頻率等于激振器固有頻率時，吸振器減振效果最好，然而激振頻率稍有變化，其減振效果大幅降低，甚至引起主系統共振。通過調節剛度，可以改變吸振器固有頻率，使吸振器在寬頻帶上對主系統進行有效減振。圖4做出了吸振器在不同剛度下主系統的幅頻特性曲線。

由于剛度可連續變化，故在最小、最大剛度下，主系統幅頻特性曲線“波谷”形成頻帶，即吸振器有效減振頻帶，如圖5所示。

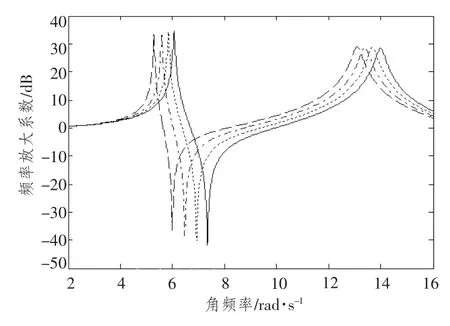
圖4 不同剛度下主系統幅頻特性曲線Fig.4 Amplitude-versus-frequency curve of primary system in different stiffness

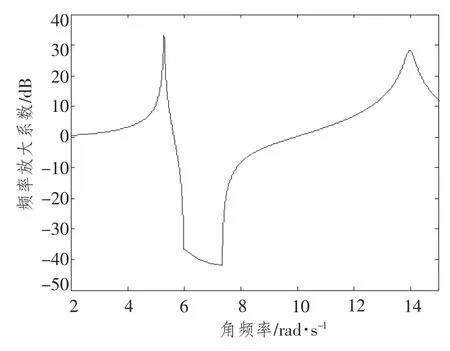
圖5 連續調節剛度時主系統幅頻特性曲線Fig.5 Amplitude-versus-frequency curve of primary system in continuously adjustable stiffness

為便于觀察變剛度吸振器減振效果，圖6 給出了主系統的時域響應圖。圖中，仿真初期吸振器固有頻率不等于激振頻率，主系統振幅較大，在200 s附近調節吸振器剛度，當其固有頻率等于外界激振頻率時，主系統振幅明顯降低。

圖6 主系統時域振動響應Fig.6 Vibration response of primary system in time

通過上述分析可知，變剛度吸振器可以實現對外界激振頻率的追蹤，有效拓寬減振頻帶，充分發揮吸振器的減振性能，這對于工程實際具有重要意義。

3 基于磁流變彈性體變剛度動力吸振器的實驗研究

為研究基于MRE 變剛度動力吸振器的寬頻減振性能，本部分搭建實驗系統，具體如圖7所示。工作過程為:激振器接受信號發生器的信號帶動主系統振動，傳感器采集主系統振動信號經電荷放大器給數據采集儀，對信號進行快速傅里葉分析，數據存儲單元對信號存儲并得出主系統的幅頻特性曲線。實驗中做出了電流為0 A，0.5 A，1 A和1.5 A 時主系統的幅頻特性曲線，具體如圖8所示。由圖8可知，在電流從0 增大到2 A的過程中，吸振器固有頻率(曲線最低點)由23.48 Hz 增加到28.38 Hz，其減振頻帶得到有效拓寬。

圖7 基于MRE的吸振器實驗系統Fig.7 DVA experimental system based on MRE

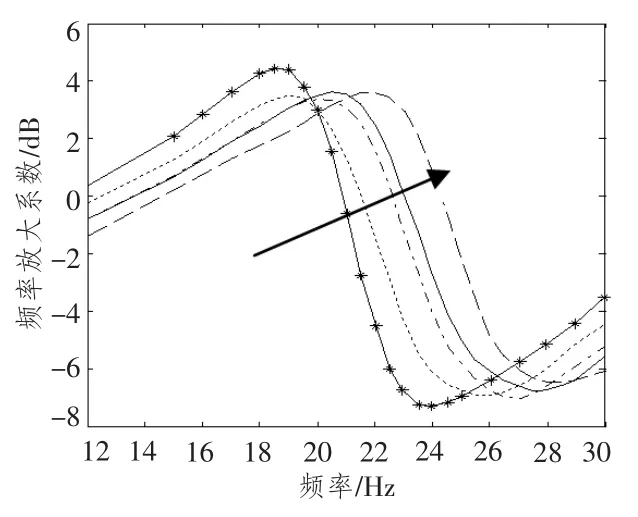
圖8 不同電流下主系統幅頻特性曲線Fig.8 Amplitude-versus-frequency curve of primary system in different current

基于吸振器的反共振減振原理，由主系統幅頻響應可知，曲線最低點處的頻率即為吸振器固有頻率，結合不同電流下主系統幅頻特性曲線可找到吸振器固有頻率與電流的關系，具體如表2所示。

表2 吸振器固有頻率與電流間關系Tab.2 The relationship between natural frequency of DVA and current

由數據擬合兩者關系如圖9所示。

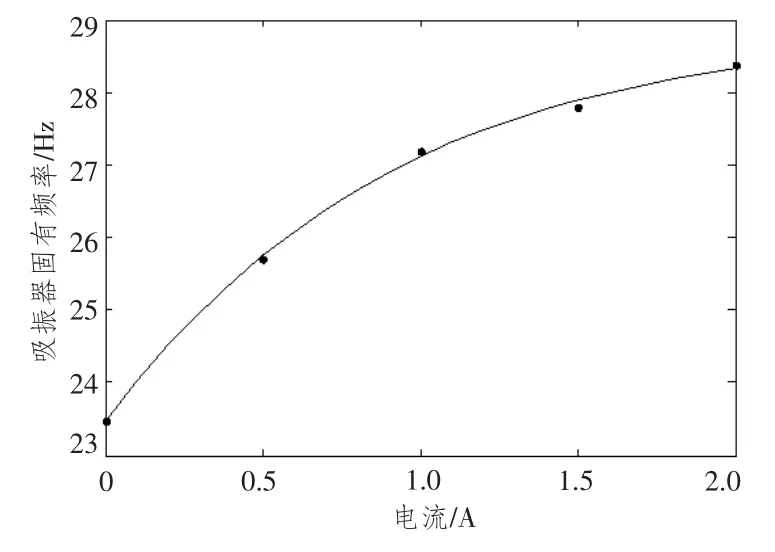
圖9 吸振器固有頻率與電流關系Fig.9 The relationship between natural frequency of DVA and current

由上述吸振器固有頻率與電流的關系曲線，分析主系統在變剛度吸振器作用下的振動情況。使主系統在任意激振頻率下振動，當吸振器固有頻率不等于激振頻率時，利用上述曲線調節電流，以調節吸振器固有頻率，實現對外界激振頻率的追蹤，做出主系統的時域響應圖，如圖10所示。

圖10 主系統時域振動響應Fig.10 Vibration response of primary system in time

由時域圖可知，在24 s 之前，吸振器固有頻率與外界激振頻率不等，主系統振幅為1.83，在24 s 調節電流，以實現吸振器對外界激振頻率的追蹤，當主系統穩定后，振幅為1.04，幅值降低約43.2%。這說明通過調節吸振器剛度，使其固有頻率等于外界激振頻率，可有效抑制主系統振動。

4 結 語

文章設計研究了一種基于磁流變彈性體的變剛度動力吸振器。利用磁流變彈性體剛度可控的性能，有效拓寬了吸振器的減振頻帶。仿真和實驗證明，設計的吸振器可通過調節電流來改變剛度，以實現對外界激振頻率的追蹤，充分發揮了吸振器的減振性能。幅頻特性曲線表明，設計的吸振器減振頻帶達5 Hz;時域圖表明，當外界激振頻率不等于吸振器固有頻率時，可通過調節剛度來改變吸振器固有頻率，實現對外界激振頻率的追蹤，使主系統的振幅降低約43%。這說明對于受變頻激勵的系統，本文所設計的吸振器具有良好的減振性能。

［1］FRAHM H.1911，“Device for Damping Vibration of Bodies”，US patent:989958.

［2］任明章.動力吸振器及其應用［M］.北京:機械工業出版社，2013.

［3］WILLIAMS K，CHIU G，BERNHARD R.Adaptive-passive absorbers using shape-memory alloys［J］.Journal of Sound and Vibration，2002，249(5):835－848.

［4］GAO Qiang，ZHANG Wei-feng，et al.An adaptive tuned vibration absorber based on variable mass［J］.Noise Control Eng.J，2011，59(5).

［5］DENG H X，GONG X L，WANG L H.Development of an adaptive tuned vibration absorber with magnetorheological elastomer［J］.Smart Materials and Structures，2006，15:111－116.

［6］FRANCHEK M A，RYAN M W.AdaPtive passive vibration controlcJournal of Sound and Vibration，1995，189(5):565－585.

［7］WALSH P L.A variable stiffness vibration absorber for minimization of transient vibration［J］.Journal of Sound and Vibration，1992，158(2):195－211.

［9］龔興龍，鄧華夏，李劍峰，等.磁流變彈性體及其半主動吸振技術［J］.中國科技大學學報，2007，37(10):1192－1203.GONG Xing-long，DENG Hua-xia，LI Jian-feng，et al.Magnetorheological elastomers and corresponding semiactive vibration absorption technology［J］.Journal of University of Science and Technology of China，2007，37(10):1192－1203.

［10］仲維暢.磁偶極子與磁粉探傷［J］.無損檢測，1990，12(3):66.ZHONG Wei-chang.Magnetic dipole and magnetic particle inspection［J］.Nondestructive Testing，1990，12(3):66.

［11］DENG Hua-xia，GONG Xing-long.Application of magnetorheological elastomer to vibration absorber ［J］.Communications in Nonlinear Science and Numerical Simulation，2008(13):1938－1947.