例說多元初等函數結構的化解策略

●江志杰(惠安縣第三中學福建惠安362100)

例說多元初等函數結構的化解策略

●江志杰(惠安縣第三中學福建惠安362100)

以xi(其中i=1，2，…，n)為變量的基本初等函數，經過有限次的四則運算或復合運算，且可用一個式子表示的函數y=f(x1，x2，…，xn)，稱為多元初等函數.近年來各地高考屢屢以多元函數模型為載體，綜合考查函數的單調性、最值、導數及其應用等基礎知識，著力考查推理論證能力、運算求解能力、知識交匯遷移能力和創新意識等，有效考查函數與方程、化歸與轉化、分類與整合、數形結合等數學思想.這對以一元函數為主體的傳統函數教學有著極大的挑戰和跨越，為此筆者著重從多元初等函數結構入手，談談其化解策略.

1 配湊換元轉化為一元函數

有些二元函數y=f(x1，x2)經過適當的整理變形后，可令其中或t=x1x2或t=x1±x2等，轉換為關于t的一元函數y=φ(t)來解決，這是一種最常規的化歸策略.

例1設A(x1，y1)，B(x2，y2)(其中x1＜x2)是函數f(x)=xlnx－x+1圖像上的2個點，且曲線f(x)在點T(t，f(t))處的切線與直線AB平行，求證:x1＜t＜x2.

解由kAB=f'(t)得

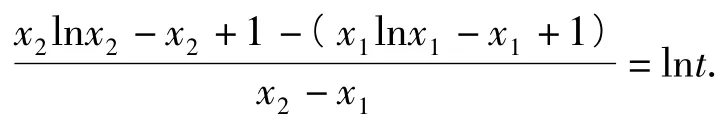
本題關鍵是證明關于t的函數

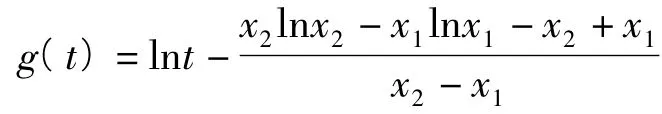
在(x1，x2)上有零點.注意到g(t)在(x1，x2)上單調遞增，于是問題轉化為判斷端點值g(x1)，g(x2)的符號.而

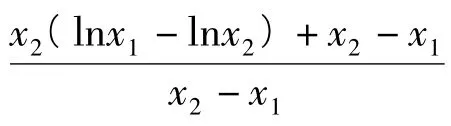
的右端是二元“準齊次”的分式結構，分式上下同除以x2得

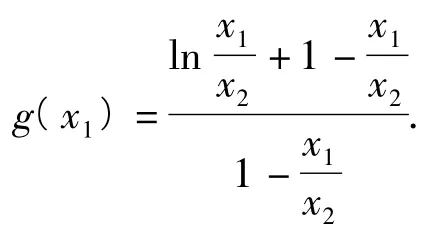
點評解決本題的另一關鍵就是要明確字符t，x1，x2，λ的“身份特征”，如在初始函數

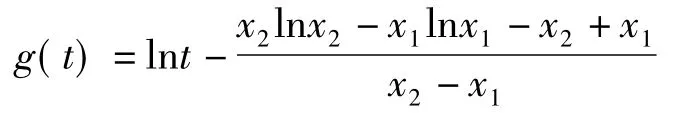
中t是自變量、未知量，x1，x2是常量;然而在二元函數

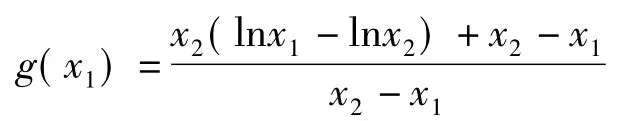
中，x1，x2是自變量的“身份”;λ是換元簡化后一元函數的自變量.因此，只有把握前后函數的“主元”，方能抓住解決問題的核心和本質.

變式設A(x1，y1)，B(x2，y2)(其中x1＜x2)是函數f(x)=eax－x(其中a≠0)圖像上的2個點，記直線AB的斜率為k，問:是否存在x0∈(x1，x2)，使得f'(x0)＞k成立?若存在，求x0的取值范圍;若不存在，請說明理由.

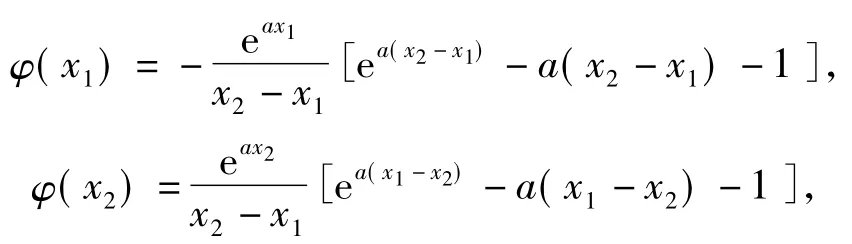
點評本題解析中φ(x1)，φ(x2)的配湊整理和分離一元函數F(t)=et－t－1的模型是問題解決的最大“亮點”.

2 更換主元演變為一元函數

多元初等函數y=f(x1，x2，…，xn)經常根據實際需要，比如將x1視作變量，其余x2，…，xn視作常量，即可實現轉化為一元函數y=φ(x1)的形式.

如例1中:

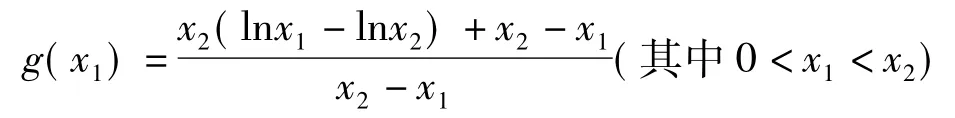
的符號由分子x2(lnx1－lnx2)+x2－x1的符號所確定.若將x1視作自變量、將x2視作常量，則可得一元函數

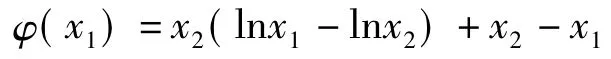
(其中x1∈(0，x2)，x2為常量)，對x1求導得

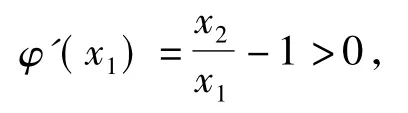
故函數φ(x1)=x2(lnx1－lnx2)+x2－x1在(0，x2)上單調遞增，且用x2替代x1得端點值φ(x2)=0，于是φ(x1)＜0，g(x1)＜0.同理可得g(x2)＞0.

3 利用單調性定義建構函數

某些二元不等式左、右2邊具備鮮明的同構性，比如f(x1)＞f(x2)或等結構的不等式經常可建構函數模型，轉化為函數的單調性問題加以解決.

例2設f(x)=ex－a(x+1)(e是自然對數的底數，e=2.718 28…)，且f'(0)=0.

1)求實數a的值，并求函數f(x)的單調區間;

2)設g(x)=f(x)－f(－x)，若曲線y=g(x)上任意不同的2個點連線的斜率恒大于實數m，試求實數m的取值范圍.

分析1)a=1，f(x)的單調遞增區間為(0，+∞);單調遞減區間為(－∞，0).

2)依題意得，對任意x1，x2∈R(其中x1＜x2)，恒有成立，即

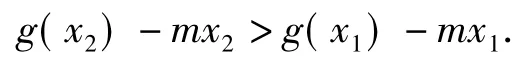
構造函數F(x)=g(x)－mx，則F(x)在R上單調遞增.因此

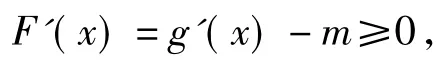
即m≤g'(x)在R上恒成立.而

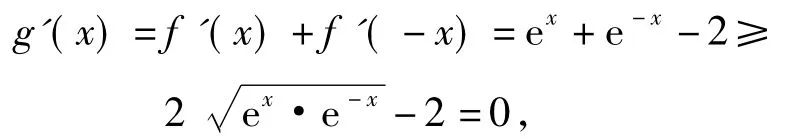
當且僅當x=0時，取到等號，故m≤0.

4 挖掘目標函數式幾何意義

有些多元函數y=f(x1，x2，…，xn)本身蘊含著某種特殊結構(如2個點間的距離或距離平方或2個點的斜率等形式)，具有豐富的幾何意義.倘若我們能充分發揮數形結合思想，必將巧妙有效地開辟新的解法空間.

例3若實數a，b，c，d滿足(b+a2－3lna)2+(c－d+2)2=0，則(a－c)2+(b－d)2的最小值為______.

解目標多元函數(a－c)2+(b－d)2表示點(a，b)與點(c，d)之間距離的平方，由已知條件得

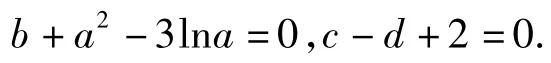
即點(a，b)，(c，d)分別是曲線y=－x2+3lnx與直線x－y+2=0上的動點，因此本題的關鍵是求曲線y=－x2+3lnx上的點與直線x－y+2=0上點的距離的最小值.設曲線y=－x2+3lnx在點P(m，n)處的切線與直線x－y+2=0平行，則

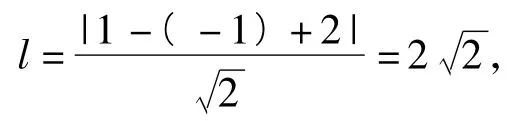
從而(a－c)2+(b－d)2的最小值為8.

例4已知正數a，b，c滿足:5c－3a≤b≤4c－a，clnb≥a+clnc，則的取值范圍是______.

解本題關鍵在于挖掘條件中多元不等式的內涵:5c－3a≤b≤4c－a，clnb≥a+clnc可化為

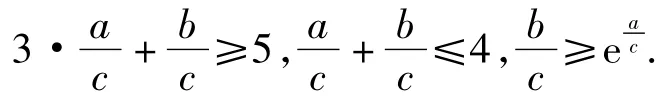
作出(x，y)所在平面區域(如圖1).過原點作曲線y=ex的切線，設切點為P(t，et)，則

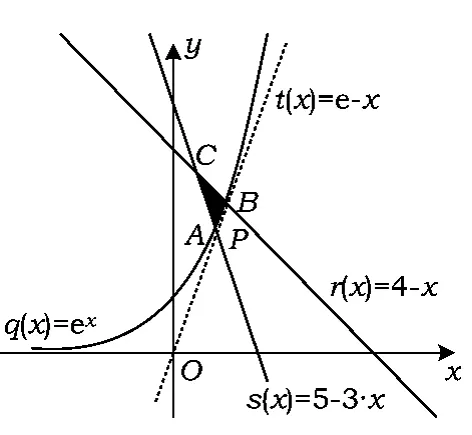
圖1

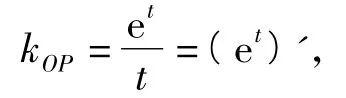
解得t=1，kOP=e.

點評在研究某些多元函數結構問題時，如果單純從代數的角度去分析思考，往往很難找到正確的解題途徑.這時若能根據函數式的結構特征，聯想到與之相應的幾何背景、幾何模型，就可使問題迎刃而解，體現出簡捷、明快、精巧、創新的數學風格.

5 分離提煉隱藏函數

有些多元方程f(x1，x2，…，xn)=0中，當取區間內的某一值時，相應地總有滿足這一方程的唯一的xj(其中j∈{1，2，…，n})存在，那么多元方程f(x1，x2，…，xn)=0在該區間確定了一個隱藏函數xj=φ(xi)(其中i，j∈{1，2，…，n}(i≠j)).通過分離提煉隱藏函數xj=φ(xi)，從而實現問題的化解.但要注意有時隱藏函數xj=φ(xi)的確定顯化是有困難的，甚至不可能的.

例5已知函數f(x)=x－aex(其中a∈R，x∈R).若函數y=f(x)有2個零點x1，x2，且x1＜x2.

1)求a的取值范圍;

3)證明:x1+x2隨著a的減小而增大.

(2014年天津市數學高考理科試題)

解1)由f(x)=x－aex，可得

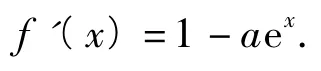
下面分2種情況討論:

①當a≤0時，f'(x)＞0在R上恒成立，可得f(x)在R上單調遞增，不合題意.

②當a＞0時，令f'(x)＞0得x＜－lna，令f'(x)＜0得x＞－lna.因此f(x)的單調遞增區間是(－∞，－lna)，單調遞減區間是(－lna，+∞).依題意得f(－lna)=－lna－1＞0，解得0＜a＜e－1，即a的取值范圍是(0，e－1).

2)由x1－aex1=0得x1是自變量a的函數，2邊關于a求導數得

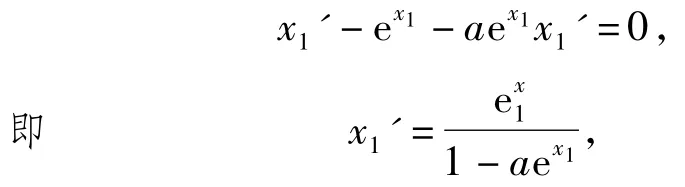
由第1)小題可知

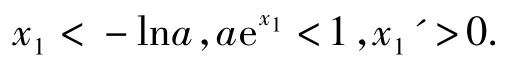
同理可得x2'＜0，即當自變量a的值減小時，x1的值減小，x2的值增大，從而(其中x1＞0，x2＞0)的值增大.

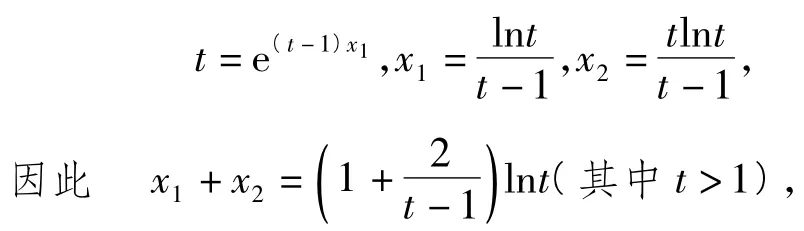
易知x1+x2在t∈(1，+∞)上隨著t的增大而增大.而t隨著a的減小而增大，故x1+x2隨著a的減小而增大.

結束語多元函數結構的化解問題其實是個廣泛而籠統的話題，在高中數學考查中屢屢涉及，著實讓廣大師生深感棘手茫然.但只要精心剖析多元結構式的本質特征或鮮明特點，巧妙靈活地通過換元、分離或提取等一系列措施，有效轉化為一元函數問題解決，將一元函數的思想方法淋漓盡致地滲透或遷移在多元函數問題中，就能很好地解決，而這種處理方式也正符合高中數學新課程所提倡的高層次能力要求.