運用馬爾科夫鏈進行學習狀態變化趨勢分析的一種方法*

◆劉歌 劉鳳祥 杜春雁 楊琪 田振清

運用馬爾科夫鏈進行學習狀態變化趨勢分析的一種方法*

◆劉歌 劉鳳祥 杜春雁 楊琪 田振清

探討基于馬爾科夫鏈對學生群體學習成績狀態變化過程及其趨勢進行分析的一種方法，給出具體應用實例。不難推斷，通過對研究對象變化過程的細致刻劃，可給出群體狀態向量間接近或偏離的速度，據此判斷教學方法改革的迫切性與適應性。

馬爾科夫鏈；學生群體；學習狀態

1 引言

馬爾科夫鏈是一個建立在隨機過程上的數學模型。其本質是一種概率估計，它將狀態序列看作一個隨機過程，通過對事物不同狀態的初始概率及狀態之間轉移概率的研究，預測事物的未來狀態[1]。在教學過程中，諸多研究對象的形成過程可以看成或近似為隨機過程，出于研究者對研究對象發展變化狀況分析的需要，使得馬爾科夫鏈在教學領域中得到廣泛應用[2]。

運用馬爾科夫鏈方法時，對于學生群體學習狀態變化趨勢的過程分析建立在兩次相鄰測驗的基礎上，若采用同一標準將不同班級前后兩次測驗成績分成不同等級，給出狀態向量，依據等級的變化情況，可以構建出每一班級的轉移矩陣。將第一次測驗成績的等級分布作為初始向量，在假設教學水平穩定的情況下，由初始狀態向量經轉移矩陣估算出每次轉移后每個班級的狀態向量，從而對學生群體學習狀態變化趨勢進行過程分析、比較判斷[3]。

已有的論文研究主要關注變化的最終狀態，進行的教師教學質量評價是終結性評價。由于缺乏對狀態變化過程的描述，其應用價值有限。運用馬爾科夫鏈分析方法，通過對研究對象變化過程的細致刻劃，可給出研究對象的接近或偏離的速度，據此判斷教學方法改革的迫切性與適切性。

2 二維狀態向量分析方法

為簡化考慮，本文以二維狀態向量為例，通過兩個群體的比較實例，闡釋相應分析方法。不難想象，該方法可方便地推廣到三維、四維乃至更高維的狀態向量變化趨勢分析上。

設M、N分別表示兩學生群體的狀態向量，每一向量可用其模長和方位角加以描述，比較兩向量應同時考慮模長及其夾角。圖1給出兩狀態向量M、N間位置關系。

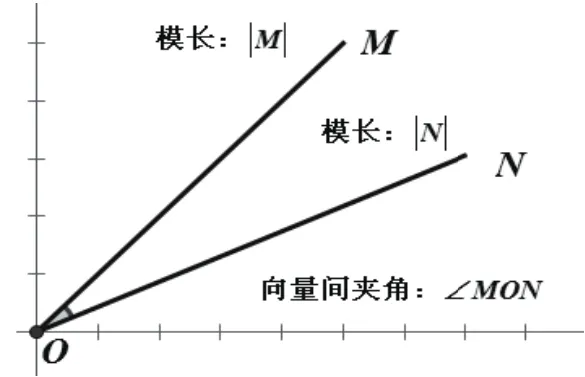
圖1 狀態向量M、N模長及夾角位置關系示意圖

作者：劉歌、劉鳳祥、杜春雁、楊琪，內蒙古師范大學在讀研究生，研究方向為遠程教育；田振清，通信作者，內蒙古師范大學教授，主要從事遠程教育研究（010022）。

若|M|=|N|，并∠MON≈0，則意味兩個學生群體此時學習狀態向量最為接近；

若|M|≠|N|，并∠MON≠0，則意指兩個學生群體此時學習處于不同狀態，夾角越大，表明這兩個群體差距越大。

設有甲乙兩個班級，學習狀態向量變化趨勢大致存在三種情況：

甲班初始成績很好，但學習成績變化處于下降狀態，而乙班初始成績低于甲班，但乙班的成績變化處于上升狀態，經有限次轉移，狀態逐漸接近；

甲班學生不僅初試成績好于乙班，并且成績一直處于上升狀態，而乙班一直處于下降狀態（或保持基本不變），

經有限次轉移，兩班狀態偏離程度愈加增大；

甲、乙兩班成績無論是上升或是下降變化小、幅度隨機波動，雖經多次轉移變化，狀態仍相對保持不變。

1）設甲乙兩班現都有20名學生，對他們的學業成績進行測驗，簡單地將測得的成績分為兩個等級（60分以上為及格，60分以下為不及格）。甲班前測18名學生及格，2名學生同學不及格；后測有16名學生及格，4名學生不及格（有2名學生由及格到不及格）。以M表示甲班學業成績的狀態向量，則M0=(0.9,0.1)，M1=(0.8,0.2)，由此可構建轉移矩陣：

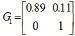
利用轉移矩陣G1，可推算出甲班學生后續的成績狀態向量（見表1）。

乙班前測及格3人，不及格17人；后測及格5人，不及格15人。以N表示乙班學業成績的狀態向量，則N0=(0.15,0.85) ，N1=(0.25,0.75)，則乙班的轉移矩陣：

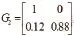
同理，利用轉移矩陣G2，可推算出乙班學生后續的成績狀態向量（見表1）。

計算狀態向量M、N的模長、夾角、模差||M|-|N||等數據，如表1所示。

依表1，繪制向量模長及夾角變化過程示意圖，得圖2（a）～（d）。

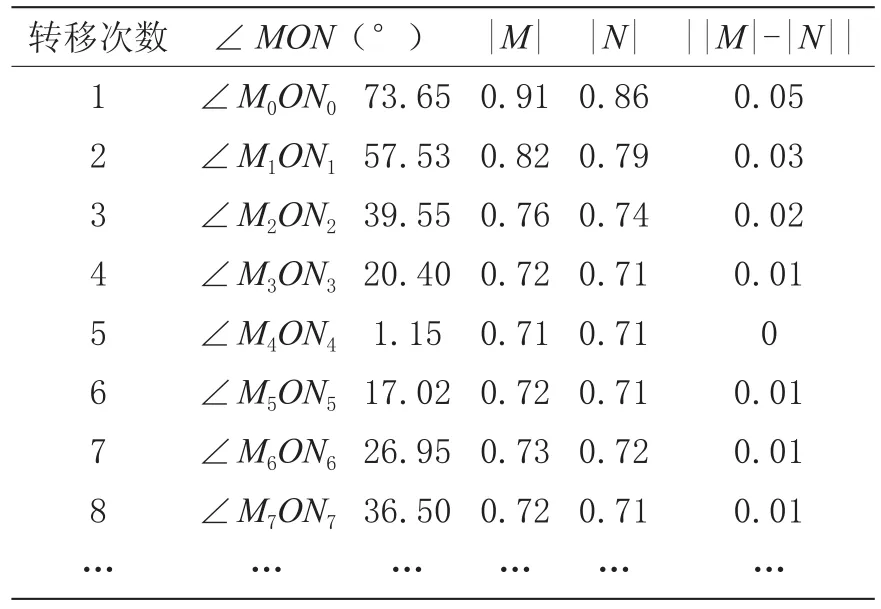
表1 兩狀態向量間接近—相等—偏離數據表

由圖2（a）表示起始時兩向量間夾角較大；（b）顯示轉移中甲乙兩班狀態向量夾角逐漸變小，模差的絕對值也逐漸減小；（c）表明經過5次轉移后，兩班狀態向量夾角、模差的絕對值最為接近，說明兩班此時學習狀態基本相同；（d）意味依此繼續轉移下去，甲乙兩班狀態向量夾角又逐漸變大，此時乙班成績超過甲班成績。

2）設甲班前測及格11人，不及格9人，進行后測，及格人數為13人，不及格7人；乙班前測及格10人，不及格10人，后測及格人數為8人，不及格為12人，則甲乙兩班轉移矩陣分別為：

狀態向量變化趨勢如表2所示。

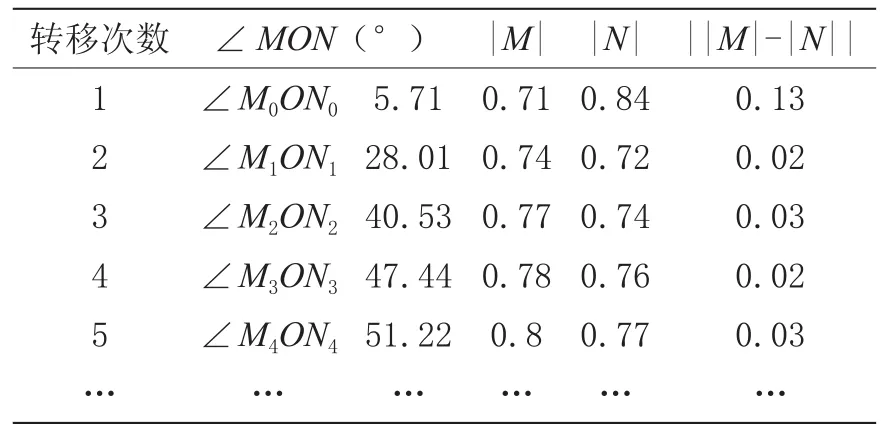
表2 兩狀態向量間偏離增大數據表

依表2，繪制向量模長及夾角變化過程示意圖，得圖3（a）～（c）。

圖3（a）～（c）顯示，甲乙兩班起始狀態向量不同，且甲班的成績不僅初始成績好于乙班，每次轉移后的成績都呈更好的趨勢，而乙班每次轉移后的狀態變得越來越差，隨轉移次數的增加，兩向量夾角愈加增大。

3）若依轉移矩陣估計甲乙兩班的狀態向量，每次轉移后兩班狀態等級變化幅度都不是很大，會出現甲乙兩班的狀態向量之間的夾角、模差的絕對值變化很小（或基本保持不變）的情況，意指兩班學生的學習狀態相對保持不變，不出現接近或偏離的態勢（圖略）。

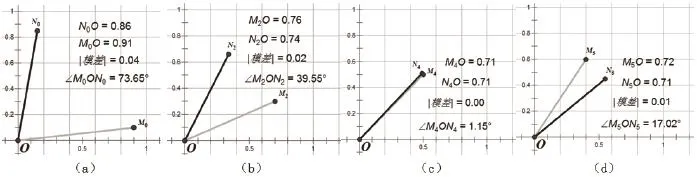
圖2 兩狀態向量間趨向相等后差距變大的過程

3 結語

上述討論簡單地將兩班學生的成績劃分為兩個等級，給出二維狀態向量，藉此說明分析的方法。顯然，這種分析過程同樣可以應用于將狀態劃分為三等級（三維向量）、

四等級（四維向量）乃至更多的等級（更高維向量）的情況，且分析的班級亦不必局限為兩個群體。

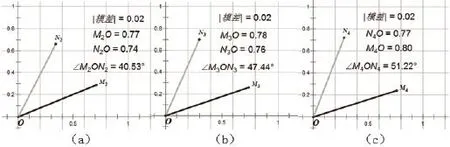
圖3 兩狀態向量間偏離加大

運用馬爾科夫鏈分析方法，通過對不同群體變化過程趨勢的細致刻劃，可估計狀態向量間接近或偏離的速度[4]。當速度較大時，提示教學方法改革的迫切性；至于相對緩慢的速度，則說明教學方法的效應并不顯著，需要相當長的時間才會出現一定程度的積累性后效。

[1]夏秀芳,房圓圓.馬爾可夫預測模型在人力資源預測方面的應用[J].青島建筑工程學院學報,2001,22(2):75-77.

[2]惠淑榮,董建國.馬爾科夫鏈在教學評價中的應用[J].高等農業教育,2009(10):60-63.

[3]鄭勇輝,鄭石英,孫駿.基于馬爾科夫鏈的研究型教學模式教學成效評價分析[J].高等教育研究學報,2012(6): 61-63.

[4]田振清,邊琦.關于學生復雜連鎖反應時間分布模型參數估計的一種方法[J].內蒙古師范大學學報:自然科學漢文版,2014,43(4):448-453.

Method of Learning Process State Change Trend Analysis based on Markov Chain/

/LIU Ge, LIU Fengxiang, DU Chunyan, YANG Qi, TIAN Zhenqing

This article discusses a method for the analysis based on Markov chain to the students learning state change process and its trend, and gives a concrete example.

Markov chain; student groups; learning state

G642.0

B

1671-489X(2015)18-0096-03

內蒙古師范大學教學研究項目“形成性評價工具軟件的設計開發與應用研究”（137153）。

10.3969 /j.issn.1671-489X.2015.18.096