靜電場與萬有引力場的類比探討*

◆張國前

靜電場與萬有引力場的類比探討*

◆張國前

類比是物理學中的一個重要思想方法。在靜電場和萬有引力場中，從基本的實驗定律、宏觀特征量的定義、實體性的描述，到主要規律的表述及證明、典型應用等，既表現出很多的相似性，又表現出不同的個性。通過類比，加深對物理概念的深入理解，滲透物理學的思想方法。

靜電場；萬有引力場；類比

類比法是人類認識客觀世界的一種基本思維方法，是根據兩個(或兩類)對象之間在某些方面的相同或相似而推出它們在其他方面也可能相同或相似的一種推理方法。物理學上許多重要理論，都是通過類比提出假設，然后經過實踐檢驗發展成為科學理論的。其中萬有引力場與靜電場的發現及其規律的認識，類比的思想方法起了非常積極的作用。

在大學物理教材中，靜電場和萬有引力場分別在電磁學和力學部分討論，而且力學是以力為主線展開，沒有突出場的特性。如果注意到靜電場和萬有引力場的聯系，應用類比的方法，盡可能還原科學家發現規律及逐漸深化認識的過程，可以幫助學生感受和體會物理科學的閃光思想和方法，并由此及彼，更加深入系統地掌握物理規律，促進學生提高思維能力。

1 奠基性的實驗定律

萬有引力定律和庫侖定律都是人們熟悉的物理規律。萬有引力定律最早由牛頓于1685年發表在其名著的《自然哲學的數學原理》一書中。它指出，任意兩個質點之間都存在相互作用的引力，定量表達式為：

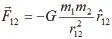
1785年，庫侖發現兩個靜止點電荷之間的相互作用規律，即庫侖定律。定量表達式為：

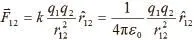
比較萬有引力定律與庫侖定律，首先表達式非常相似，相互作用力的大小都滿足平方反比關系，與點的量的乘積成正比，方向沿聯線方向，質點模型和點電荷模型都是當實物的限度與距離相比很小時的理想化；其次，庫侖力的大小與電荷移動無關的特性又和萬有引力的大小與質點移動無關的特性類似；再次，兩個定律都是通過觀察和實驗總結出來的經驗定律，不是什么理論的邏輯結果，但它們分別是整個經典力學理論和經典電磁學理論的基礎，有著奠基性的作用；最后，兩個定律常數的首次精確測定，都是通過扭秤實驗完成的，設備及實驗原理也很相似。

物理學史研究表明，庫侖定律的發現，很大程度上是受到萬有引力定律的啟發。1760年，D.伯努利首先猜測到電力會不會也跟萬有引力一樣，服從平方反比定律？他的想法顯然有一定的代表性，因為平方反比定律在牛頓的形而上學自然觀中是很自然的觀念，如果不是平方反比，牛頓力學的空間概念就要被改寫[1]。1775年，英國唯物主義哲學家普瑞斯特列（1733—1804）通過反復觀察小軟木球在帶電金屬罐內外不同的受力情況，以類比的思想大膽提出猜想：“難道我們就不可以從這個實驗得出結論：電的吸引與萬有引力服從同一定律？因為容易證明，假如地球是一個球殼，在殼內的物體受到一邊的吸引力，決不會大于另一邊的吸引力。”普瑞斯特列本人沒有加以證明，但卻為后來的物理學家提出一個研究的方向。1785年，法國科學家庫侖通過自行設計的“扭秤”實驗證實了普瑞斯特列的平方反比的猜想，完成了庫侖定律的定量表示式[2]。其中引力與電量成正比的假設純粹是庫侖在同牛頓萬有引力定律的類比過程中引入的[3]。

2 描述場的物理量

在牛頓力學中，牛頓把物體之間的萬有引力看成是一

種“超距作用”。這雖然是很不自然的，但是由于萬有引力理論在天體力學上取得的巨大成功使人們相信，兩個不相互接觸的點電荷之間的靜電力理所當然也是“超距作用”。近代物理學發展證明，“超距作用”觀點是錯誤的。電荷在其周圍產生電場，而電場對放入其中的電荷有力的作用。類比電場的概念，萬有引力的“超距作用”就不言自明了。

作者：張國前，寧夏師范學院物理與信息技術學院教授，研究方向為物理教學論（756000）。

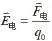
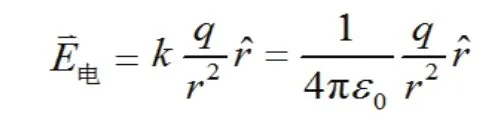
與點電荷的電量成正比，與距離的平方成反比，方向沿徑向。這樣，在以點電荷為球心的同一球面上各點的電場強度大小相等，滿足球對稱性。

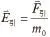
電場滿足疊加原理，這是庫侖力疊加性的必然結果。從萬有引力定律和力的疊加原理出發，同樣可推知，引力場也滿足疊加原理。

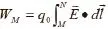
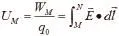
引力場中引入引力勢物理量，同樣表征引力場的能量特性。與靜電場類比推導，引力場中以N點為引力勢零點，則M點的引力勢為：

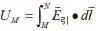
對于地球，可看成是質量均勻分布的球體，周圍的引力勢相當于質量集中到球心的質點產生的引力勢。通常選地球表面為零參考點，在地面高度為h的地方，引力勢：

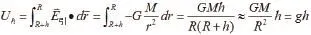
3 場遵循的主要規律

高斯定理 靜電場遵循高斯定理：通過一個任意閉合曲面的電通量φE等于該面所包圍的所有電量的代數和除以ε0。即：

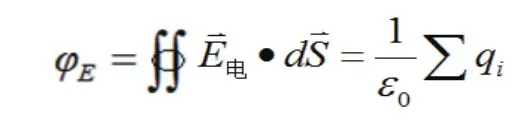
對于連續帶電體：

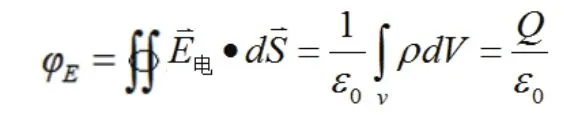
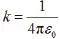
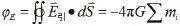
即引力場強在任意閉合曲面上的通量等于該閉合面包圍的所有物體的質量和乘以-4πG，與閉合面外的質量無關。

類比于靜電場高斯定理的證明方法[4]，引力場強的高斯定理是很容易證明的，故不做詳細證明。

4 典型例子——球殼和球體的電場與引力場類比

在靜電場中，應用高斯定理能方便求得電荷分布具有一定對稱性的帶電體產生的電場分布。如對于帶電量為Q的均勻帶電球殼、均勻帶電球體，利用高斯定理可求得它們產生的電場分布情況分別是：

理這個問題，但是只是習慣于用高斯定理解決靜電場的問題，從引力場的角度解決問題還不大習慣。當然，可以用積分法做證明，詳細的步驟可參考資料[5]。

5 小結

牛頓在發現萬有引力定律時曾面臨這樣一個問題：地球對地面上物體引力的距離為什么要從地心算起？這在牛頓時代是個不小的難題，牛頓自己發明了微積分把它解決了。這里已清楚地證明，從外邊看，球對稱物體（帶電體）產生的引力（電力）作用，就像其質量（電量）集中在球心一樣。應用高斯定理，可以用對稱的方法非常簡捷地處

類比推理對科學的發展起著積極的推動作用。正如麥克斯韋所說：“我認為依靠物理的類比，一門科學的規律與另一門科學的規律之間的部分類似，將使我們能從這兩門科學中的一門科學來說明另外的一門科學。”[6]通過萬有引力定律與庫侖定律的相似之處，由靜電場的電場強度、電勢概念引入引力場強度和引力勢，對引力場從力和能兩個方面進行描述，得到引力場類似于負電荷的電場的結論；由靜電場的高斯定理、環路定理得到引力場的高斯定理和環路定理，進一步認識了兩種場的有源性和無旋性，因此可以利用靜電場中已學會的方法去處理引力場的問題，如在求解某些具有對稱性的物體與質點的萬有引力時，利用引力場的高斯定理能大大簡化計算。

[1]郭奕玲.物理學史[M].2版.北京:清華大學出版社, 2005:91.

[2]朱鋐雄.物理學思想概論[M].北京:清華大學出版社, 2009:87.

[3]朱榮華.物理學基本概念的歷史發展[M].北京:冶金工業出版社,1987:92.

[4]趙凱華.新概念物理教程電磁學[M].2版.北京:高等教育出版社,2006:23.

[5]趙凱華.新概念物理教程力學[M].2版.北京:高等教育出版社,2004:339.

[6]蔡香民.萬有引力與高斯定理:類比在物理學中的應用[J].安徽師范大學學報:自然科學版,2002(2).

Analogical Discussion on Electrostatic Field and Gravitational Field/

/ZHANG Guoqian

Analogy is an important perception method in physics. The basic laws of experiment, the definition of macroscopic characteristic quantities, the substantive description and the expression and application of principal rules are all showed many similarities and different characteristics. The physics concept and its ideas can be comprehended deeply by analogy.

electrostatic fi eld; gravitational fi eld; analogy

G642.423

B

1671-489X(2015)18-0154-03

寧夏2012年高等學校教學質量與教學改革工程項目；寧夏師范學院重點科研項目（ZD2011003）。

10.3969 /j.issn.1671-489X.2015.18.154