淺議如何培養學生的數學思維能力

楊雪麗

摘 要：數學思維教育主要是通過數學教學體現出來的，那么如何把傳授知識和培養思維能力二者相統一起來就是進行數學思維教育的主攻方向。要培養學生的數學思維能力，就要培養學生學習數學的興趣，培養學生綜合應用數學知識的能力，培養學生的創新能力。

關鍵詞：興趣；創新；綜合應用

數學思維能力的培養，在數學教學中是普遍受到重視的問題。傳統做法是把思維變成思路，進而成為可傳訊物。有的教師認為，既成思路因題而異，把它傳授給學生可以使思維教育的內容豐富多彩。然而，思維主要是靠啟迪，而不是靠傳授，越是傳授得一清二楚，學生就越不需要思維。即使傳授的東西是范例，也僅增加了知識的儲存，而不一定能使人在新情境下索解。那么教師啟迪學生思維的工作應表現在哪些方面？為此，我提出以下幾條建議僅供參考。

一、培養學習數學的興趣

1.引導學生愛好數學。有的學生認為數學是枯燥的、貧乏的，甚至呆板的。其實不然，數學是一門趣味十足的學科。教師在教學中可引導學生多閱讀一些集知識、智力、趣味為一體的課外讀物，這樣既可開闊學生的視野，激發學生的興趣，還可使學生獲得主動全面的發展。

如下例：奶奶和王梅一起烙餅。她們家烙餅的平鍋每次只能放四張餅，烙一面需要4分鐘，奶奶烙四張餅的正反面用去8分鐘，再烙兩張餅又用去8分鐘，這樣奶奶烙六張餅共用去了16分鐘。但王梅用的方法與奶奶的不同，烙相同數量的餅，用的時間卻少。你知道王梅用什么方法嗎？

其實，這是一個數學中較有趣的統籌方面的題。王梅是先在平鍋上烙四張餅的一面，用去4分鐘，然后把兩張餅翻過來烙，另外換上兩張沒有烙過的餅。又用去4分鐘，兩張餅烙好了，其余四張餅都只需要烙一面就行了。這樣，王梅烙6張餅共用了12分鐘，比奶奶少用4分鐘，既節省了時間，又節約了燃料，一舉兩得。

實際上，數學時時刻刻都存在于我們的日常生活中，與我們的生活是密切聯系的。只要貼近生活，善于觀察、思考，同樣也能激發學生愛好數學。

2.創設成功教育的氛圍，激發學生的興趣。一位詩人說：“幸福”的日子使人聰明。教師要有意識地營造使學生不斷取得思維成就的環境，讓學生不斷地在思維成功的幸福中良性循環，越學越想學，越思越靈活。

如：先讓學生做這樣的一個題：

1+2+3+…+100=？

學生一看，馬上就知道等于5050，因為從1到100連加可看作50個101相加，即50×101=5050。

接著再讓學生做：

1-2+3-4+…+97-98+99-100=？

學生看一眼，不一定都能立刻得出結果，但仔細看題就會發現每連續兩項之差都為-1，并且共有50組這樣的數，即可看作50個-1相加，結果就為50×（-1）=-50。

做到這，學生已開始嘗試到成功的喜悅了。若此時：再讓學生做：1+2-3-4+5+6-7-8+…+97+98-99-100=？

由于學生已有解上兩題的經驗，因此他們大多立刻就能看出每連續四項之和為-4，這樣的數共有25組，結果就為25×（-4）=-100。

這樣，學生獲得了成功，學習數學的興趣就更濃了，學習效果也就提高了。同時，也能引導學生積極地去探索和發現，從而培養他們探索思維的激情。

二、在教學過程中，培養學生綜合應用數學知識的能力

在數學教學過程中，要培養學生的數學思維能力，僅僅是培養學生的學習興趣還不夠，還要培養學生的綜合應用能力。這即能促使學生全面發展，還能較大程度地提高學生的數學思維能力。

如：有的平面幾何問題的證明，可以根據幾何量之間的關系，通過代數中的恒等變形或建立幾何量之間的方程式來進行研究。

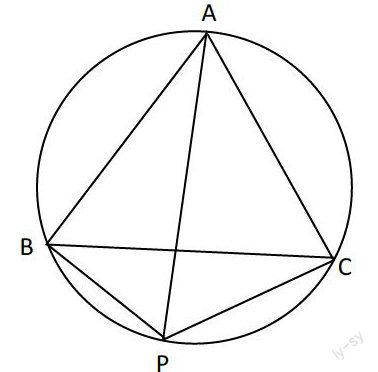
例：設P是正△ABC外接圓的弧BC上的 一點，如圖所示：

求證：（1）PA=PB+PC （2）AB2=PA2-PB﹒PC

分析：因為要證的兩個結論可分別化為：

PB+PC=PA， PB﹒PC= PA2- AB2

它與代數方程中韋達定理的形式很相似，因而只要能證明PB和PC都是一元二次方程x2-PA﹒x+（PA2-AB2）=0的根即可。即該題可利用代數思想建立幾何量之間的方程來求證。

證明：∵△ABC是正三角形

∴∠ABC=∠ACB=60°

∵點A、B、P、C四點共圓

∴∠APB=∠ACB=60°

∠APC=∠ABC=60°

在△ABP中，由余弦定理得

AB2=PA2+PB2-2PA﹒PB﹒cos60°

= PA2+PB2-PA﹒PB

∴PB2-PA﹒PB+（PA2-AB2）=0

即：PB是方程x2-PA﹒x+（PA2-AB2）=0的根。

同理，在△ACP中PC是方程x2-PA﹒x+（PA2-AC2）=0的根

∵AC=AB

∴PC是方程x2-PA﹒x+（PA2-AB2）=0的根

根據韋達定理可得：

PB+PC=PA， PB.PC= PA2-AB2

即： PA = PB+PC， AB2= PA2- PB.PC 得證

當然，上例只是數學中綜合應用的一個方面，要培養學生的數學思維能力，還要進行全面的系統的訓練。

學生有了一定的綜合應用能力之后，要提高數學思維水平，還要學會創新。

三、培養學生的創新能力

培養學生的創新能力，我認為主要是培養學生在學習活動中能積極地、主動地去進行探索，敢于大膽地去突破各種已有的條條框框的束縛。

下面就引用美國一位教師的做法來簡要地闡述這一問題。

這位教師給學生出了這樣一個題：每箱桔汁都裝有24瓶，為了使250個學生人手一瓶，共需要多少箱？

從傳統的觀點看，這是一個除法的問題。但這位教師并沒有直接寫出相應的算式：“250÷4=？”而是寫了如下的表達式：“250？24”，其目的就是為了讓學生“自由地”去進行探索。結果，有些學生用加法——對24進行連加直至達到250，求得了解答；有些學生用減法，也就是從250連續減去24直至最終達到0；甚至還有學生利用乘法但無法求得解答。在所有的學生當中，還有一個女生提出了如下的求解方法：100包括4個25，由于250個學生是兩個100再加上半個100，因此，如果每箱桔汁都裝有25瓶的話，相應的結果是4箱加4箱再加2箱（總共10箱），但現在每箱只有24瓶，也就是每箱少一瓶，那么就必須在第11箱中補取10瓶。

由此可看出，這種主動的、積極的探索對于學生在數學上培養思維能力是十分有益的。當然，在這一點上還有待于所有的教學工作者進一步地摸索、探討。

培養數學思維能力，也就培養了人本質地看問題的意識，培養了良好的思維習慣，形成良好的思維策略，進而擴展人們頭腦中的數學空間。總之，數學思維能力的培養是一項長期的艱巨任務。對于如何培養學生的數學思維能力，我所提的幾種做法還不全面，還有待于在數學實踐中繼續探索總結。

參考文獻：

[1]郭思樂、喻緯 《數學思維教育論》 上海教育出版社.

[2]鄭毓信 《數學教育：從理論到實踐》 上海教育出版社.