案例教學法在現(xiàn)代控制理論中的應用研究*

◆周磊 陳桂 湯玉東

案例教學法在現(xiàn)代控制理論中的應用研究*

◆周磊 陳桂 湯玉東

針對現(xiàn)代控制理論專業(yè)課課堂教學中的常規(guī)教學法，提出案例教學法。對閉環(huán)控制系統(tǒng)的極點配置的教學內(nèi)容，其理論性比較強，授課內(nèi)容比較枯燥，如果采用常規(guī)教學法，學生學習興趣不濃，學習積極性不高，導致課堂學習效率低下。針對這種現(xiàn)象，將案例教學法引入課堂教學中，通過對自動檢測系統(tǒng)狀態(tài)反饋極點配置問題的講解，能夠加深學生對課堂理論知識點的理解，提高課堂聽課效率。

現(xiàn)代控制理論；案例教學法；自動檢測系統(tǒng)

10.3969/j.issn.1671-489X.2015.24.103

1 前言

現(xiàn)代控制理論課程是工科院校自動化及相關(guān)專業(yè)的一門重要專業(yè)課程，也是自動控制原理的后續(xù)課程［1］。同時它也是一門理論性很強的專業(yè)課程，其內(nèi)容非常抽象，難以理解，包含大量復雜的數(shù)學公式和推導證明。如果采用傳統(tǒng)的教學方式，教師寫板書、學生記筆記都很費時，授課信息量不大，學生聽課枯燥無味，課堂效率不高［2-3］。針對這種現(xiàn)象，在現(xiàn)代控制理論的教學中引入案例教學法，不僅能使學生獲得基本的控制理論知識、加強學生對理論知識點的理解，而且在解決問題的過程中還能使學生理論聯(lián)系實際，培養(yǎng)學生的動手和創(chuàng)新能力。

2 現(xiàn)代控制理論課堂教學知識點舉例

在由宋麗蓉主編的《現(xiàn)代控制理論基礎(chǔ)》第五章第二節(jié)“閉環(huán)系統(tǒng)的極點配置”的課堂教學中，教師會提到控制系統(tǒng)的動態(tài)性能在很大程度上取決于閉環(huán)系統(tǒng)的極點位置。對于單輸入單輸出系統(tǒng)而言，如果采用自動控制原理中的輸出反饋控制，不能做到閉環(huán)極點的任意配置，即不一定將閉環(huán)極點配置到所希望的位置。狀態(tài)空間描述是對系統(tǒng)的一種完整描述，反映了系統(tǒng)外部輸入變量、輸出變量和系統(tǒng)內(nèi)部狀態(tài)變量之間的關(guān)系。狀態(tài)反饋是從系統(tǒng)的狀態(tài)變量處引出反饋，因此，狀態(tài)反饋是一種完全的系統(tǒng)信息反饋，而輸出反饋則是系統(tǒng)信息的一種不完全反饋。為了使反饋系統(tǒng)能獲得更好的動態(tài)性能，宜采用狀態(tài)反饋［4］。

閉環(huán)系統(tǒng)的極點配置問題就是通過對狀態(tài)反饋矩陣的選擇，使閉環(huán)系統(tǒng)的極點配置在所希望的位置上，從而達到一定性能指標的要求。把閉環(huán)系統(tǒng)的極點配置到任意所選位置時，要求系統(tǒng)是狀態(tài)完全能控的。常規(guī)教學法對任意極點配置的充要條件是系統(tǒng)狀態(tài)完全能控給出理論證明，對狀態(tài)反饋矩陣的計算也給出數(shù)學推導，由于涉及大量數(shù)學推導和計算，對學生的數(shù)學要求較高，因此會讓學生對這個知識點產(chǎn)生較難的錯誤感覺，也激發(fā)不了學生的學習興趣。可見采用常規(guī)教學法，學生很難理解和掌握狀態(tài)反饋器的設計原理和方法。利用案例教學法能夠更簡單和直觀地讓學生理解這個知識點，而不必一直糾結(jié)于數(shù)學推導的方法。

3 案例教學法的引入

案例教學法是最早由美國哈佛商學院所倡導的一種很獨特的案例型教學方法，有助于培養(yǎng)和發(fā)展學生主動參與課堂討論，提高課堂聽課效率［5-6］。案例教學法直到20世紀80年代才開始實施于普通教育學，目前為世界各國所倡導。

本文以自動檢測系統(tǒng)為案例，設計自動檢測系統(tǒng)通過直流電機驅(qū)動一組測試探針，來檢測開關(guān)面板上的各種開關(guān)、繼電器和指示燈等元件。檢測系統(tǒng)的方框圖如圖1所示，其中K為所需的功率放大系數(shù)。對圖1所示的檢測系統(tǒng)設計狀態(tài)反饋器，以便滿足時域性能指標的設計要求，可以分為以下五個步驟［7-8］。

圖1 直流電機的開環(huán)方框圖

建立開環(huán)系統(tǒng)的狀態(tài)空間模型 由開環(huán)系統(tǒng)方框圖可知系統(tǒng)是一個三階系統(tǒng)，可以取三個狀態(tài)變量，這里選取x1=θ，x1=if，根據(jù)狀態(tài)變量之間的關(guān)系可得復數(shù)域的代數(shù)方程組：

將上述代數(shù)方程組兩邊時域化，可得開環(huán)系統(tǒng)的狀態(tài)方程為：

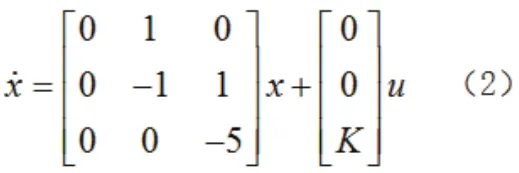
由圖1可知，開環(huán)系統(tǒng)的輸出方程為：y=x1（3）

開環(huán)系統(tǒng)的能控性 由線性控制系統(tǒng)的能控性秩的判據(jù)可得：

由于式（4）中K≠0，因此開環(huán)系統(tǒng)狀態(tài)完全能控，能夠進行狀態(tài)反饋器的設計，將極點配置在所希望的位置。

建立閉環(huán)系統(tǒng)的狀態(tài)空間模型 設所選取的狀態(tài)變量都可以用于反饋，于是系統(tǒng)的反饋控制信號u為：

引入狀態(tài)反饋后閉環(huán)系統(tǒng)的方框圖如圖2所示。

為了使系統(tǒng)產(chǎn)生精確的位置輸出，可取k1=1，將反饋控制信號u和k1=1代入式（1）中，可以得到：

得到閉環(huán)系統(tǒng)的特征方程為：

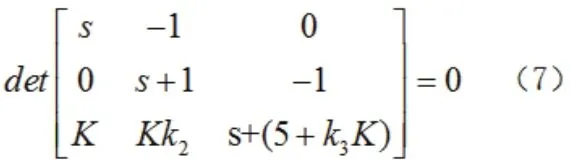
由動態(tài)性能指標確定希望的閉環(huán)極點 系統(tǒng)的設計目標是系統(tǒng)階躍響應的調(diào)節(jié)時間小于2 s（Δ=±2%），超調(diào)量小于4%。

超調(diào)量公式：

圖2 直流電機的閉環(huán)系統(tǒng)方框圖

這里采用MATLAB計算：

所以ξ＞0.7156

將特征方程改寫成適合繪制根軌跡的形式：

取a=8和b=20，即閉環(huán)系統(tǒng)的零1，2=-4±j2。根據(jù)k2=0.35和k3=0.05，可以得到閉環(huán)系統(tǒng)的根軌跡圖（圖3）。

由圖3可知，當Kk3=12時，系統(tǒng)的三個閉環(huán)極點分別為s1，2=-3.69±j2.99和s3=-10.62，這時系統(tǒng)的阻尼比為ξ=0.777，滿足系統(tǒng)對超調(diào)量的要求。

確定閉環(huán)系統(tǒng)的輸出 引入狀態(tài)反饋后，閉環(huán)系統(tǒng)的階躍響應曲線如圖4所示。從圖4中可以看出，當k1=1，k2=0.35，k3=0.05和K=240時，系統(tǒng)的超調(diào)量為2%，調(diào)節(jié)時間為1.6 s。這表明上述設計方案能夠滿足性能指標的設計要求。

圖3 閉環(huán)系統(tǒng)的根軌跡圖

圖4 閉環(huán)系統(tǒng)的階躍響應曲線圖

4 結(jié)論

綜上所述，本文以采用狀態(tài)反饋控制對閉環(huán)極點任意配置為例，將該教學內(nèi)容理論和實際應用緊密聯(lián)系，并且采用的案例是學生所熟悉的自動檢測系統(tǒng)，對系統(tǒng)性能比較了解，學生學習的積極性很高，該知識點學生設計的方案可以有多種。將案例教學法引入到現(xiàn)代控制理論課堂教學中，相對于傳統(tǒng)教學法，更容易激發(fā)學生聽課的積極性和提高課堂聽課效率，達到較好的教學目的，同時也提高了學生的動手和創(chuàng)新能力。■

［1］Ogata K.現(xiàn)代控制工程［M］.北京:電子工業(yè)出版社，2014.

［2］王冬梅，劉帥師，等.現(xiàn)代控制理論課程教學改革探索［J］.長春工業(yè)大學學報，2011，32（3）:49-51.

［3］魏龍生，等.及時教學法在現(xiàn)代控制理論中的教學研究［J］.中國電力教育，2013（32）:120-121.

［4］Dorf R C， Bishop R H.現(xiàn)代控制系統(tǒng)［M］.北京:電子工業(yè)出版社，2015.

［5］李明，劉洪山.案例教學法在“計算機控制技術(shù)”課程中的應用［J］.中國電力教育，2009（2）: 65-67.

［6］米智楠，潘柳萍，陳龍安.案例教學法在“自動控制原理”課程教學中的應用［J］.中國電力教育，2010（33）:87-88.

［7］周磊，宋麗蓉，陳桂.MATLAB在現(xiàn)代控制理論教學中的應用［J］.中國現(xiàn)代教育裝備，2008（5）:109-110.

［8］李武，榮軍，丁躍澆.現(xiàn)代控制理論課程實驗的對比教學法［J］.實驗技術(shù)與管理，2015，32（6）:204-207.

Application Study of Case Teaching Method in Modern Control Theory

Z HOU Lei， CHEN Gui， Tang Yudong

For the conventional methods of modern control theory course， the paper proposes a case teaching method. The teaching content of state feedback pole assignment of closed-loop control system has very strong theory and the teaching content is relatively empty. If using the conventional teaching methods， the students’learning interest and initiative are not high， leading to low classroom teaching ef ciency. Through the explanation of state feedback pole assignment problem for automatic detecting system， it is proved that the case teaching method can deepen the students’ understanding of classroom theory knowledge and improve the students’ ef ciency in classroom lectures.

modern control theory； case teaching method； automatic detecting system

G642.4

B

1671-489X（2015）24-0103-03

*項目來源：江蘇省研究生教育教學改革研究與實踐課題（基金編號：JGZZ15_109）；南京工程學院教學改革重要項目（基金編號：jg201306）；南京工程學院教學改革項目（基金編號：jg201411）。

作者：周磊，南京工程學院副教授，研究方向為非線性控制、智能控制等；陳桂，南京工程學院教授，研究方向為非線性控制、智能控制等；湯玉東，南京工程學院副教授，研究方向為智能控制（211167）。