復習課“活動場”中的“五場協同”

張旭蘭

最近再次閱讀顧飛宇先生的《協同教育的101個視角》這本書，仔細琢磨書中關于高效課堂“活動場”中“五個場”的部分內容，聯系前段時間上的一節復習課，感觸頗多。

顧先生認為高效課堂的“五個場”：課堂教學的形態是教學問題場、教學情景場、教學情境場、個體意境場和個體意向場嵌套層疊、和諧交互作用的動態過程，每一個學生得到和諧發展的動態過程。教師，學生，每個人對同樣的教育資源都有不同的理解，不同的理解完全可以“和而不同”。從不同的角度看到的課堂模式結構的內在規律是相同的。我的復習課《平面圖形的面積》經歷了這豐富的“活動場”中的“五場協同”。

一、“備學交流”中的“五場協同”

《平面圖形的面積》這節課的教學目的重在通過引導學生回憶和整理平面圖形的周長和面積計算公式及其推導過程，并讓學生能熟練地應用公式進行計算。繼而引導學生探索知識間的相互聯系，構建知識網絡，從而加深對知識的理解，并從中學會整理知識，領會學習的方法。課前，我給學生布置了如下備學作業：

1.在小學階段，我們學過哪些平面圖形？什么叫平面圖形的面積？

2.各種平面圖形的面積計算公式是怎樣的？它們是怎樣推導出來的？

3.發現哪三個問題值得進一步討論？

課始，交流備學中發現的問題。每一位同學都在小組里和同伴進行了問題的交流（問題場），把自己難以理解的問題提出來和同伴一起在小組里解決。因為是復習課，每一個學生都進行了備學，大家都是有備而來，有話可說（情景場），這個時候課堂處于“問題場”“情景場”交互的狀態。很快，小組交流結束，我組織全班歸納（情境場），同學們運用轉化的思想，將學習過的所有平面圖形的面積計算公式建構成了這樣一幅知識網絡圖（意境場）。這個時候應該是以上“四場”嵌套層疊、和諧交互作用的狀態。

這幅圖印在每個學生的頭腦里，聯系學生腦中所有與之相關的思維模塊，每個學生的聯系思維模塊的數量、聯系的方式、聯系的程度是不一樣的。這種不一樣就是“個體意境場”。在生活中遇到相應的數學問題，激活這個意境場中的一些思維模塊來思考數學問題，這些被激活的思維模塊就是個體意向場了。生活中的數學問題經過這“五場”的協同過程，正是生活問題數學化的過程。

二、“質疑問難”中的“問題再生”

我理解的教學問題場、教學情景場、教學情境場、個體意境場和個體意向場是可以同時貫穿整節課的。在“質疑問難”環節，和諧組的小飛同學突然提出一個問題：“圓環的周長怎樣算？”這一問題，“一石激起千層浪”，同學們展開了激烈的討論。這種狀態是又一次“五場協同”。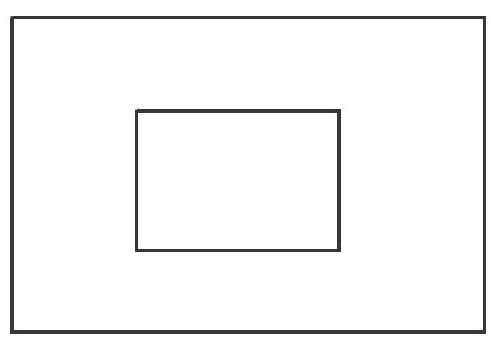

有些同學認為“圓環的周長等于外圓的周長加上內圓的周長”，另一些同學認為“圓環的周長應該就是外圓的周長”，也有同學認為，有時候圓環的周長指的是內圓的周長，還有同學認為“圓環只求面積，不求周長，因為求周長沒有實際意義”。我與學生一起回到對“周長”定義的理解：環繞有限面積的區域邊緣的長度積分，叫作周長，圖形一周的長度，就是圖形的周長。周長的長度因此亦相等于圖形所有邊的和。

根據周長的定義，對于一個圓環來說，是圍繞圖環所有邊線的總長，那圓環的周長就是用大圓周長加小圓周長。這樣來理解是否就比較妥當了呢？同學們還是爭執不下。

持不同說法的同學們，分別找出了能夠證明自己觀點的生活中的數學題。

生1：縫紉師傅要做一個圓環玩具，他要做的最基本的動作就是要縫好外圓的周長，再縫好內圓的周長。所以，圓環的周長=外圓周長+內圓周長。

生2：用一根鐵絲圍成一個內半徑是2米，外半徑是4米的環形區域，需要多長的鐵絲？這里要求的鐵絲的長度，就是外圓的周長加上內圓的周長，所以，圓環的周長=外圓周長+內圓周長。

生3：有一個圓形的池塘，半徑8米，在池塘的四周有一條2米寬的小路，求小路的周長。此時的小路呈現出圓環形，要求小路的周長是要求半徑8米的圓的周長，還是半徑是10米的圓的周長，還是用外圓周長加內圓周長呢？這道題對于我們六年級學生來說，非常簡單，仔細分析之后一定能明白，要求小路的周長就是要求半徑為10米的圓的周長。也就是這時候圓環的周長等于外圓的周長。

生4：小時候玩的鐵環，要求鐵環的周長。鐵環的周長是外圓的周長，還是內外圓周長之和？顯然，此時可忽略內圓的周長，只要求外圓的周長就可以了。

生5：假如一個操場的跑道是圓環形的，那么操場跑道的周長應該怎樣求呢？是求內圓的周長，還是求外圓的周長，還是外圓周長加內圓周長呢？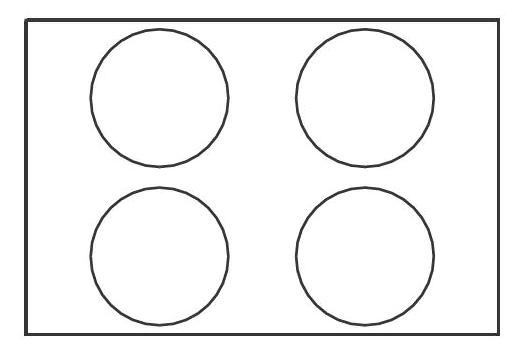

就5位同學的題來討論，還有些學生是這樣思考的：“周長是不是需要一筆畫出來？”“用‘圓環周長等于外圓與內圓周長之和這樣算出來的圓環的周長太長了，不符合題意。”“定義是封閉圖形一周的長度，不是兩周哦。”“要么算外周長，要么算內周長，只能算一樣。”“我認為生3的題其實是讓求大圓的周長，是因為題出得不嚴謹。”“生5的題中如果把問題改成一圈最長能跑多遠？一圈最短能跑多遠？是不是會更妥當一些？”“知道圓環是什么樣子了，沿著連線描一圈，這一圈的長度就是周長。”……

三、“問題解決”中的“豁然開朗”

怎樣的說法能解決所有學生提出的問題？第三次“五場協同”開始了。按照“環繞有限面積的區域邊緣的長度積分，叫作周長。圖形一周的長度，就是圖形的周長。周長的長度因此亦相等于圖形所有邊的和”來理解，圓環的周長應該是用外圓的周長加上內圓的周長。那為什么學生們找到的這些生活中的數學問題，看來與之產生矛盾了呢？看似同樣是求圓環的周長，有的可以理解為求外圓的周長，還有的可以理解為求內圓的周長呢？

因此，圍繞周長的定義，我們再次理解：“環繞有限面積的區域邊緣的長度積分，叫作周長，圖形一周的長度，就是圖形的周長。周長的長度因此亦相等于圖形所有邊的和。”在小學階段，我們學習了長方形、正方形、平行四邊形、三角形、梯形還有圓這些平面圖形，這些平面圖形都是“實心圖形”，不難理解“環繞有限面積的區域邊緣的長度積分，叫作周長，圖形一周的長度，就是圖形的周長。”還可以更簡單地描述為“圍成一個平面圖形所有邊長的總和，叫作這個圖形的周長。”如果是非實心的圖形，或稱之為“空心圖形”呢？怎么算周長？有一個孔的“空心圖形”，有多個孔的“空心圖形”，它們的周長怎么算？

我引導學生復習轉化的策略，學生一下子明白了，可以把空心圖形轉化為實心圖形來計算周長！圓環可以轉化成兩個實心圓來計算周長。“環形的周長”包含兩個周長，圓環的外圓周長是大圓周長，圓環的內圓周長是小圓周長，圓環的總周長就是大圓周長加小圓周長。

四、“建構模塊”中的“舉一反三”

這是第四次“五場協同”了。

引導學生理解之后，出示下圖：

在一個長12厘米、寬8厘米的長方形紙中間，剪掉一個長6厘米、寬4厘米的長方形，求剩余部分的周長。

學生們已能自己分析：1.這是一個空心圖形，由兩個圖形組成；2.這個圖形的周長是兩個圖形的周長之和。這就是解決空心圖形周長的數學模型。用這個數學模型，好學的學生們又一起討論了下面這道題：

在一個長方形紙上，剪掉4個圓，剩下圖形的周長是多少？

此時，這道題的分析變得易如反掌：1.這是一個空心圖形，由5個基本圖形組成；2.這個圖形的周長是5個圖形的周長之和。

數學家弗賴登塔爾說：“數學來源于現實，也必須植根于現實。”作為一名數學老師，我們在數學教學中，要把數學知識與生活實際、學生的數學學習有機地結合起來。一方面，我們要引導學生充分挖掘生活中的數學問題，創設生動有趣的問題情境來幫助學生學習，鼓勵學生善于發現生活中的數學問題；另一方面，要讓學生對數學有“源頭”意識，努力引導學生發現那些客觀上的存在，不斷發現蘊含在數學問題中的一些基本數學模型，讓數學模型溝通著現實中的生活世界和數學中的抽象世界，把抽象的、不那么抽象的及具體的解題方法聯系在一起進行分析，獲得探索數學的體驗，提高利用所學的數學知識解決實際問題的能力，在讓“數學問題生活化”的同時，很好地實現“生活問題數學化”。