基于電動汽車的無刷直流電機低扭矩脈動混合矢量驅動控制

張立偉 毛學宇

（北京交通大學電氣學院 北京 100044）

0 引言

對于無刷直流電機（Brushless Direct Current Motor，BLDCM）來說，轉矩脈動抑制一直是該研究領域的重要課題。BLDCM 轉矩脈動按產生原因可分為電磁脈動和電流換向脈動。電磁脈動主要涉及到電機繞組與轉子磁場設計問題，當前主要通過對電機電磁結構進行優化設計，改進或是減小這種電磁引起的轉矩波動。電流換向脈動是BLDCM 繞組電流導通換向過程中產生的電流脈動，進而造成電磁轉矩脈動，當前主要有Kwang-Woon Lee 等學者提出的電流反饋法[1]、謝楊梅提出的滯環電流法[2]、重疊換相法以及PWM 斬波法[3-5]。也有學者提出在人工智能的基礎上實現專家系統、基于模糊集合理論的模糊控制、基于神經網絡的神經化控制等[6]，以減小這種換向轉矩脈動。文獻[7]提出了一種新的基于電流預測控制的新方法，以使非換相電流保持恒定。文獻[8]提出了一種針對常規空間矢量脈寬調制（Space Vector Pulse Width Modulation，SVPWM）中零矢量u0和u7的工作時間平均分配的特點引入了一個正比于u7工作時間的系數k0，并發現k0取不同值時可以實現多種PWM 調制方式，因此提出了一種統一PWM 的概念。文獻[9]通過對5種PWM 調制方式的分析比較，得出PWM-ON 調制方式較理想，能夠有效抑制電機的換相轉矩脈動。文獻[10]在PWM-ON 的調制基礎之上，提出了一種新型的控制方式，使關斷相電流下降速率與導通相電流上升速率相同，從而減小了換相轉矩脈動。而實際上，永磁無刷電機是一種交流電機，具有非線性、強耦合、時變性的特征，且電機運行過程中還會受到各種外界環境的干擾，因此如果按照常態化的控制策略對永磁無刷電機進行控制，不能實現高性能的控制需求。再者常態化控制策略要么只是針對特定的對象，要么需要較好的參數辨識，要么對電流傳感器、速度傳感器等傳感器要求較高[11,12]，成本高、實用性差。

為了減小換向時刻的電流突變，近些年提出了正弦波電流驅動方案[13]，這些方案并沒有在理論上深入分析轉矩脈動成因，因而效果不盡一致。另外正弦波電流驅動一般需要較為精確的轉子位置信息，依靠低成本霍爾位置傳感器來估算轉子位置，在起動時刻無法準確跟蹤，從而降低起動轉矩性能。

本文對BLDCM 的換向轉矩脈動進行分析，研究了反電動勢寬度與波形畸變對轉矩脈動的影響。經過逐一推導分析，提出了幾種不同的驅動控制策略。最后通過比較分析，并結合這幾種驅動策略的優勢，提出了一種基于低成本霍爾位置傳感器的BLDCM 混合矢量驅動控制策略。

1 BLDCM 方波驅動轉矩脈動分析

1.1 換向狀態

當BLDCM 以方波電流驅動時，實際因繞組呈現為感性，使得導通電流無法突變，尤其在換向期間，因為其他相無法理想通斷導致非換向相繞組電流擾動，進而產生換向轉矩脈動。

以圖1 為例，當S1、S4 開通時，繞組AB 相導通；S1、S6 開通時，繞組AC 相導通。換向導通階段會經歷幾個狀態，在S1、S6 開通初始階段，繞組B 相中的電流經S3 上的反并聯二極管續流，與S1、繞組A 形成回路。另一條回路由S1、繞組A、繞組C、S6 組成。這個狀態應滿足方程

圖1 換向狀態1Fig.1 Commutation state 1

式中，t 為換向狀態1 經歷時間；L 為繞組自感；M為繞組互感。定子繞組對稱且為星形聯結，有

三相繞組反電動勢為理想狀態時，有

設I 為繞組相電流穩態值，為簡化運算，忽略繞組電阻，由式（1）～式（4）可求得

此時，當S1、S6 關斷時，繞組A 中的電流會通過S2 上的續流二極管分別流經繞組B、繞組C，通過S3、S5 上的續流二極管分別與電源Udc形成回路，此換向狀態如圖2 所示。

圖2 換向狀態2Fig.2 Commutation state 2

同理，可求得繞組中電流為

式中，Ia1、Ib1、Ic1分別為 ia、ib、ic在換向狀態1到換向狀態2 的電流幅值。

由式（5），當 Udc=4Ve時，d ib/d t=d ic/dt，即在換向時 ib和 ic變化率一致，非換向相電流 ia保持恒值不變，此狀態如圖3 所示。

圖3 Udc=4Ve時，相電流變化Fig.3 Phase current variation when Udc=4Ve

在理想反電動勢情況下，可推導BLDCM 轉矩公式為

由式（7）可看出，在理想反電動勢情況下，BLDCM 的轉矩與非換向相電流成正比。在 Udc=4Ve時，非換向相電流 ia保持不變，此時轉矩無脈動。但是當 Udc≠4Ve時，相電流 ib和 ic沒有在同時達到穩定值或零值，造成非換向相電流 ia產生波動，進而造成轉矩換向脈動，如圖4 所示。

圖4 Udc≠4Ve時，相電流變化Fig.4 Phase current variation when Udc≠4Ve

由式（5）可知，在 Udc≠4Ve時，ia會產生波動。以圖4 為例，在t1'時 ic達到穩態值I，由式（5）可求出

此時ai 的波動值為

由式（9）可知，在母線電壓保持不變的情況下，相電流 ia的波動與反電動勢系數及轉速等相關。在Udc=220V，K=0.06V/(r/min)情況下，基速 ωr=1 833r/min，波動值Δia與轉速關系如圖5 所示。

圖5 aiΔ 波動值隨轉速變化曲線Fig.5 Δai fluctuations curve with the speed

由圖5 可直觀的看出，在理想反電動勢下，非換向相電流波動值隨著轉子轉速變化而變化:在0.5ωr以下時，電流波動值隨著轉速升高而降低；經過0.5ωr后，電流波動值隨著轉速的繼續升高而急劇增大。為了抑制這種非換向相電流對轉矩脈動的影響，本文通過仿真比較了理想方波電流驅動下的轉矩脈動，其值為Tes，如圖6 所示。

圖6a、圖6b 的各自的上圖為傳統方波驅動下的仿真結果，下圖為電流跟蹤控制波形以實現理想方波驅動。可以看出，傳統方波驅動下的在換向時的突變嚴重，當以理想方波驅動時，轉矩脈動得到了很好的抑制。

1.2 BLDCM 非理想反電動勢分布

實際中BLDCM 氣隙磁通密度分布并不是理想的120°梯形波分布[13]，如圖7 所示。

圖6 不同方波電流驅動時轉矩脈動對比Fig.6 Torque ripple compare in different square current

圖7 非理想氣隙磁通分布波形Fig.7 Non-ideal gap flux distribution waveform

由傅里葉分解方法可知，圖7 所示的分布波形可以看作不同頻率的正弦波合成，如式（10）所示。

式中，k 為奇數。由式（10）可知，A 相反電動勢ae為

式中，Em為反電動勢幅值。對于三相對稱分布的BLDCM，其B、C 相反電動勢be、ce 分別與ea間隔120°、240°電角度。

電磁轉矩是反電動勢與相電流共同作用的結果，通過對非理想反電動勢的傅里葉分解可知，可將其看成是基波和諧波的組成。為了方便計算，也對理想方波電流進行傅里葉分解，以A 相相電流ai為例，因為BLDCM 三相繞組按星形對稱聯結，電流分量沒有3 次及3 的倍數次諧波分量，其分解如下

式中，Imk=(4 I/π)/k，k 為奇數。對于B 相和C 相的反電動勢和電流，因為互差120°，只需將式（12）中的 ωt換成ωt-2π/3、ωt +2π/3即可得到。

參考式（7），電磁轉矩可寫為

由此可知，電磁轉矩的紋波轉矩主要為6 次基波頻率，其幅值與反電動勢和相電流的諧波幅值有關。

圖8 為理想方波電流驅動時與反電動勢波形對應圖。

圖8 反電動勢與相電流波形Fig.8 EMF and phase current waveforms

可以推導理想方波驅動時轉矩脈動隨反電動勢寬度變化的公式為

圖9 為不同反電動勢寬度下的相電流與轉矩脈動對比，從圖9 可以看出，隨著反電動勢梯形波寬度的變窄，即使以理想方波電流驅動時，轉矩脈動也會逐漸增大。

圖9 不同反電動勢寬度下的相電流與轉矩脈動對比Fig.9 Phase current and torque ripple comparison of different EMF

1.3 BLDCM 非方波電流驅動

由以上分析可知，隨著反電動勢寬度的減小，方波驅動已不能有效抑制轉矩脈動。由式（15）可以看出，影響轉矩脈動的6 次諧波含量中包含了方波電流的5 次、7 次等諧波，如果消除這些諧波的影響，即以正弦波電流驅動時，就可以減小6 次諧波含量，從而減小轉矩脈動。

由式（12）～式（14）可求得

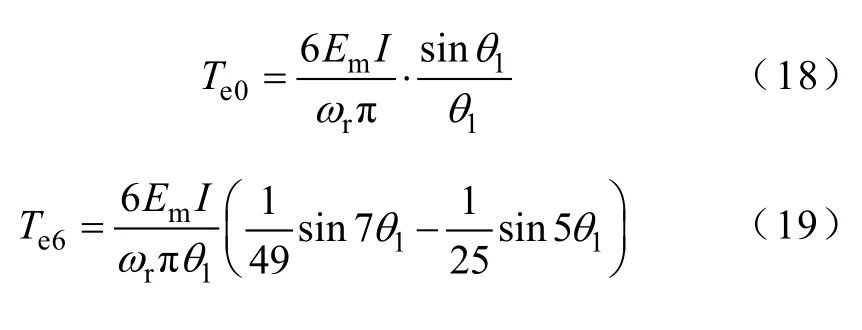
由于其他高次諧波分量幅值較小，可忽略不計，由式（18）、式（19）可求得轉矩脈動為

由 式（20）可 知，在 θ1=42°和 θ1=74°時，BLDCM 在正弦波驅動下轉矩脈動可以接近零。方波電流和非方波電流驅動兩種情況下的輸出轉矩仿真波形如圖10 所示。

圖10 兩種驅動方式輸出轉矩對比Fig.10 The comparison of torque in different injection schemes

由圖10 可以看出:非方波控制下的BLDCM 動態調速性能較好，響應迅速；六脈波方波電流驅動下的轉矩脈動為0.448 3，而相同負載情況下，非方波控制下的轉矩脈動僅為 0.091，即通過正弦波驅動，BLDCM 轉矩脈動可以大大降低。

2 BLDCM 混合矢量驅動

2.1 不同驅動方式下的轉矩性能分析

由式（13）、式（17）、式（20）得出不同驅動方式下轉矩性能對比，見表1。

表1 不同驅動策略轉矩性能Tab.1 Performance torque of different driving scheme

通過表1 中對不同驅動下轉矩脈動理論分析推導，可以得到不同驅動方式下的平均轉矩與轉矩脈動理論公式，其相應的曲線如圖11 所示。

圖11 不同驅動下的轉矩特性比較Fig.11 Performance comparison of different injection schemes in variable1θ

由圖11 可知，在反電動勢寬度為30°～60°的典型分布區間內，方波驅動下的轉矩脈動增大較快，正弦波驅動下的轉矩脈動始終為0～0.1；但方波驅動下的平均轉矩輸出始終比正弦波驅動下高10%。幾種驅動控制方式比較見表2。

表2 幾種驅動策略比較Tab.2 Performance comparison of different driving scheme

在電機起動時刻，基于60°霍爾信號無法輸出準確的位置信息，而方波驅動只需要60°分辨率的較為粗略的初始霍爾信息，且方波驅動的平均轉矩輸出都比后兩種驅動大，滿足電機起動時大轉矩輸出要求。

在BLDCM 運行時，正弦波驅動下的轉矩脈動很小，在交流電機驅動領域，正弦波矢量控制具有良好的動態調速性能，其技術已很成熟。

2.2 混合矢量驅動控制

通過上述比較分析，考慮到電動汽車實際應用與工況，在BLDCM 起動時可以方波電流驅動，在正常運行時可以正弦波矢量驅動。因此，為了保證驅動方式切換的平穩，兼顧控制系統的簡單易實現原則，本文提出一種基于混合電壓空間矢量的驅動控制策略。

對于電壓空間矢量，有一種不連續開關調制模式[14]，不同于常用的連續調制的SVPWM，這種調制方式在每一時刻有一橋臂的開關管不導通。該四開關調制模式是通過在1 個PWM 周期里，根據扇區判斷邏輯選擇插入u0或u7零電壓矢量，而不像常規SVPWM 調制方式，插入2 種零電壓矢量。所以在1 個PWM 周期里只有4 個開關操作，也稱為四開關調制SVPWM。這種調制方式下的電流趨近于方波，磁鏈軌跡為60°間隔的正六邊形，其開關損耗較連續模式下的SVPWM 減小1/3。四開關調制下的6 個非零矢量分別為

不連續調制電壓矢量空間分布如圖12 所示。

圖12 四開關調制下的電壓矢量空間分布Fig.12 The space vector in four switching modulation

在矢量切換時存在60°緩沖區間，不需要進行死區補償。與連續調制的SVPWM 建立混合電壓空間矢量，在由四開關調制切換為六開關連續調制時，只需在矢量控制系統下就可完成，易于實現。

對于四開關調制方式，表3 給出了根據扇區位置對應的開關管導通邏輯關系。

表3 轉子位置與開關管導通對應關系Tab.3 Rotor position and the switch turns on the correspondence

圖13 為混合矢量控制策略框圖，其控制模式大致如下:通過霍爾信號檢測估算轉子位置和轉速，混合SVPWM 模塊通過輸入轉子轉速信息來判斷切換驅動方式狀態（下文仿真部分給出具體的切換條件）。電機在低速起動時，驅動模式為四開關調制方波矢量驅動，該驅動模式下電機出力大、運行可靠，四開關方式和六開關方式都是按照矢量方式來控制id和iq，角度仍然采用霍爾信號檢測；順利起動后切換為六開關調制正弦波矢量控制模式，此時電機運行噪音很低，動態調速性能很好。通過下文仿真和實驗可以看出此種模式切換更平滑，轉矩脈動更小。

圖13 混合矢量控制策略Fig.13 Hybrid vector control strategy

2.3 霍爾位置信號估算

為滿足矢量控制需要的高分辨率轉子位置，本文提出基于泰勒展開式的數學解算方法來估算轉子位置。

對轉子位置θ 表達式做泰勒展開為

式中，kθ 為霍爾信號[15]跳變時刻對應轉子位置；tk為轉子在kθ 當前時刻。轉子角速度為

轉子角加速度為

由泰勒展開原理，一階轉子位置估計算法值理論上更接近于實際值θ，盡管階數增加產生的代碼運算量很大，卻可以得到更加精確的轉子位置信號。本文擬采用一階轉子位置估算算法。

由以上分析可推出一階轉子轉速和位置估計算法

此外，為了抑制估算偏差的積累，需要對轉子位置每60°進行重新校正。

圖14 為轉子位置估算對比。可以發現，在電機起動時，該算法在霍爾信號前2 個60°區間存在較大偏差，這是因為在初始時刻無法獲取轉子平均轉速與加速度。而后混合矢量以方波驅動，只需判斷霍爾信號即可，起動運行之后的估算位置信號基本上與實際轉子位置保持一致，可以實現較高精度的轉子位置輸出。

圖14 轉子位置估算對比Fig.14 The real rotor position and the estimation of rotor position

3 Matlab/Simulink 仿真驗證

為驗證本文提出的基于霍爾傳感器的混合矢量驅動方案，利用Matlab/Simulink 仿真工具搭建了控制模型。

由圖15 可知，該控制模型主要由霍爾位置信號估算模塊、混合SVPWM 驅動模塊和BLDCM 本體模塊組成，仿真電機參數見表4。

表4 仿真電機參數Tab.4 Simulation of motor parameters

圖15 混合矢量控制仿真結構Fig.15 Simulation of hybrid vector control strategy

圖16 為反電動勢寬度為100°下的仿真結果。混合SVPWM 模塊通過輸入轉子轉速信息來判斷切換驅動方式狀態，設定當轉子轉速超過500r/min 時切換為正弦波矢量控制，當轉子轉速低于480r/min時切換為方波矢量控制。由圖16c 轉速波形可以看出，BLDCM 在方波電流驅動下順利起動，再切換至正弦波電流驅動，最終加速到指定轉速。由圖16a可看出，本文提出的混合矢量控制方案在切換時刻三相線電流沒有產生突變，切換時刻轉矩保持平穩。由圖16b 可以看出，方波電流產生的轉矩脈動較大，而正弦波電流產生的轉矩脈動較小。為了盡量減少由方波驅動造成的轉矩噪聲，可以在電機順利起動后馬上切換至正弦波運行。

圖16 混合矢量控制仿真結果Fig.16 Simulation results of hybrid vector control

4 混合矢量驅動控制策略實驗驗證

本文對BLDCM 混合矢量控制系統用拖臺進行實驗驗證，實驗平臺如圖17 所示。該實驗系統由對拖電機、扭矩傳感器、BLDCM、逆變驅動控制器以及實驗數據顯示設備等組成。實驗所用BLDCM 的參數見表5。

圖17 實驗控制平臺Fig.17 Experimental test setup for evaluating the proposed method

表5 BLDCM 參數Tab.5 BLDCM parameters

(續)

圖18 為DSP 對霍爾信號在線估算得到的轉子位置信息。可以看出，通過該估算算法可以得到滿足矢量控制需要的較精確的轉子位置。

圖18 轉子位置在線估算Fig.18 The estimation results of rotor position online

圖19 為不同工況下的相電流波形與對應霍爾信號。由相電流波形可以看出，該混合矢量控制方法實現了無刷電機方波與正弦波混合驅動。通過圖19a 和圖19b 的電流切換波形對比可以看出:傳統的電流切換過程會造成一個很大的電流尖峰，致使轉矩脈動問題嚴重，而本文提出的混合矢量電壓調制方式能較好地解決切換過程中的電流脈動問題，電機平穩運行。由圖19d 可以看出，減速運行波形在轉速運行減至低速時，這種混合矢量切換也是可靠的。由圖19e 的負載突變實驗結果看出，轉子位置估算算法可以滿足混合矢量這種較大動態范圍所需的精確的轉子位置信息的要求，BLDCM 在混合矢量驅動策略下有較好的動態調速性能。圖19f 則給出了方波驅動下反電動勢與對應霍爾信號的波形。

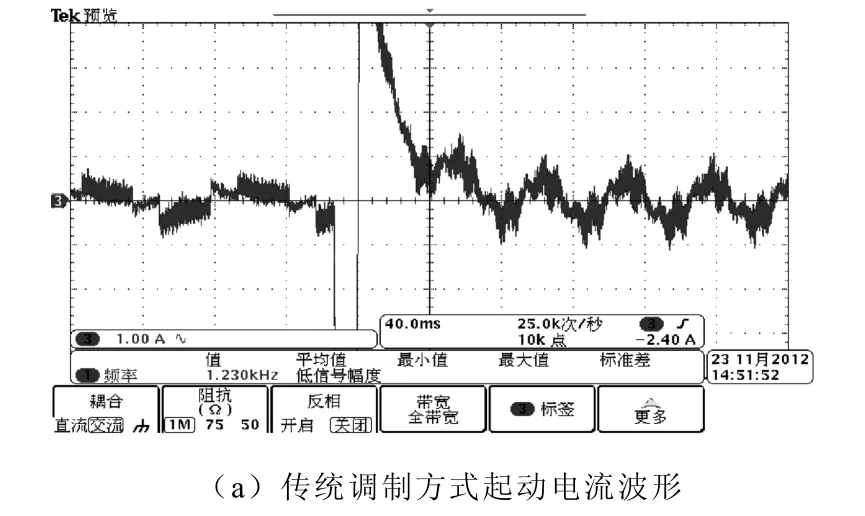
圖19 不同工況下的相電流波形與對應霍爾信號Fig.19 Measured phase current under different operating conditions correspond to hall signals

5 結論

本文首先推導和分析了BLDCM 換向轉矩脈動的產生機理與影響因素，并對這些影響因素逐一分析，并逐一研究了不同驅動控制策略，以減小換向轉矩脈動。通過比較分析與驗證，提出了混合矢量驅動控制策略，實現了低速大轉矩起動與低噪音運行。實驗結果證明，混合矢量驅動下的電機運行平穩、切換平滑、高效低噪。本文為電動汽車應用領域提供了一種全新的高性能、高可靠、低成本的BLDCM 驅動控制策略。

[1]Lee Kwang-Woon,Kim Dae-Kyong,Kim Tae-Duck.Commutation torque ripple reduction in a position sensorless brushless DC motor drive[C]//35th Annul IEEE Power Electronics Specialists Conference,Aochen,Germany,2004:283-290.

[2]謝楊梅.無刷直流電動機（BLDCM）轉矩脈動抑制的電流跟蹤型PWM 控制[J].安徽電子信息職業技術學院學報,2007,6(1):3-8.Xie Yangmei.The current tracing PWM contol of commutation torque ripple of brushless DC motors[J].Journal of Anhui Vocational College of Electrontcs &Information Technology,2007,6(1):3-8.

[3]張相軍,陳伯時.無刷直流電機控制系統中 PWM調制方式對換相轉矩脈動的影響[J].電機與控制學,2003,7(2):98-104.Zhang Xiangjun,Chen Boshi.The effect of PWM method for commutation torque ripple in the control system of BLDC[J].Electric Machines and Control,2003,7(2):98-104.

[4]Fang Jiancheng,Li Haitao,Han Bangcheng.Torque ripple reduction in BLDC torque motor with nonideal back EMF[J].IEEE Transactions on Power Electronics,2012,27(11):4630-4637.

[5]吳強,于飛.PWM 調制方式對六相無刷直流轉矩脈動的影響分析[J].海軍工程大學學報,2008,20(4):23-27.Wu Qiang,Yu Fei.The analysis of effect of PWM modulation for torque ripple of six phase DC brushless motors[J].Journal of Naval University of Engineering,2008,20(4):23-27.

[6]王曉遠,傅濤,王曉光.基于電流預測控制的無刷直流電動機換相轉矩脈動抑制[J].電工技術學報,2015,30(11):22-29.Wang Xiaoyuan,Fu Tao,Wang Xiaoguang.Current prediction control strategy for commutation torque ripple reduction in brushless DC motor[J].Transactions of China Electrotechnical Society,2015,30(11):22-29.

[7]Zhu L.Adaptive control of sinusoidal brushless DC motor actuators[D].Michigan:Michigan Technological University,2008.

[8]馬豐民,吳正國,侯新國.基于統一 PWM 調制器的隨機空間矢量調制[J].中國電機工程學報,2007,27(7):98-102.Ma Fengmin,Wu Zhengguo,Hou Xinguo.Random space vector modulation based on uniform PWM modulator[J].Proceedings of the CSEE,2007,27(7):98-102.

[9]周美蘭,高肇明,吳曉剛,等.五種PWM 方式對直流無刷電機系統換相轉矩脈動的影響[J].電機與控制學報,2013,8(2):82-88.Zhou Meilan,Gao Zhaoming,Wu Xiaogang,et al.The effect of five PWM method for comutation torque ripple of brushless DC motors[J].Electric Machines and Control,2013,8(2):82-88.

[10]王大方,卜德明,朱成,等.一種減小無刷直流電機換相轉矩脈動的調制方法[J].電工技術學報,2014,29(5):160-166.Wang Dafang,Bu Deming,Zhu Cheng,et al.A modulation method to decrease commutation torque ripple of brushless DC motors[J].Transactions of China Electrotechnical Society,2014,29(5):160-166.

[11]Won C,Song J H,Choy I.Commutation torque ripple reduction in brushless DC motor drives using a single DC current sensor[C]//IEEE 33rd Conference on Power Electronics Specialists Conference (PESC),Cairns,Queensland,Australia,2002:985-990.

[12]Kun W,Chansheng H,Zhongchao Z,et al.A novel commutation torque ripple suppression scheme in BLDCM by sensing the DC current[C]//IEEE 36th Conference on Power Electronics Specialist Conference (PESC),Recife,Brazil,2005:1259-1263.

[13]Dachin T E,Meza S,Nemes C M,et al.BLDC motor sinus driving techniques and electrical resistance evaluation[C]//IEEE International Conference on Automation Quality and Testing Robotics (AQTR),Cluj-Napoca,2012:327-331.

[14]程善美,王琰,夏麗濤,等.不連續空間矢量脈寬調制策略研究[J].微電機,2003,36(4):36-40.Cheng Shanmei,Wang Yan,Xia Litao,et al.The research of not continue pulse width modulation[J].Micromotors Servo Technique,2003,36(4):36-40.

[15]張慶超,馬瑞卿,張震,等.基于霍爾位置信號的無刷直流電機電磁轉矩觀測[J].電工技術學報,2015,30(10):187-195.Zhang Qingchao,Ma Ruiqing,Zhang Zhen,et al.Electormagnetic torque observation of bruless DC motor based on Hall position signals[J].Transactions of China Electrotechnical Society,2015,30(10):187-195.