粗糙集屬性約簡算法綜述

唐衛國張 濤羅 奕徐晉勇

（1.廣西壯族自治區右江礦務局有限公司，廣西 百色 531501；2.桂林電子科技大學，廣西 桂林 541004）

粗糙集屬性約簡算法綜述

唐衛國1張 濤2羅 奕2徐晉勇2

（1.廣西壯族自治區右江礦務局有限公司，廣西 百色 531501；2.桂林電子科技大學，廣西 桂林 541004）

屬性約簡是粗糙集理論中最核心的問題。文章闡述了基于信息熵、可辨識矩陣、遺傳算法、Johnson等粗糙集屬性約簡算法流程，指出了粗糙集屬性約簡算法的現有問題及發展趨勢，促進粗糙集屬性約簡的研究進一步發展。

屬性約簡；粗糙集理論；算法

隨著計算機網絡的高速發展，人們所要處理的數據越來越多。在大量數據中會伴有不確定問題。目前處理不確定性問題的方法主要包括概率統計、模糊理論、證據理論等[1]。但這些方法必須依靠大量的先驗知識。粗糙集理論很好彌補了以上方法缺點，可以有效處理不確定信息，卻不需要任何先驗知識[2]。

粗糙集約簡是粗糙集理論中最重要一環，包括值約簡和屬性約簡兩種。目前，大量的研究都是側重于屬性約簡[3]。屬性約簡，就是在保證系統本身含義前提下，刪除其中多余或重復的屬性，保留起決定作用的核心屬性。通過屬性約簡，可以在不改變系統本身含義的前提下得到更簡潔的決策屬性。

對于信息表I(U,A)，如果有屬性集B?A，且滿足ind(B)=ind(A)，則稱B為A的一個約簡，記為red(A)。ind(A)，ind(B)代表著A和B上的不可分辨關系。

集A所有約簡的交集稱為A的核，記為core(A)，即：

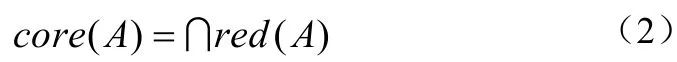
core(A)含有屬性集A的全部約簡集合中共同的等價關系，是屬性集A中最重要集合。核的定義表示了核屬性是約簡屬性集中一部分，利用核屬性可以更迅速的進行屬性約簡，改變屬性核屬性就會影響屬性約簡的前后一致性[4]。

1 粗糙集約簡算法初探

1.1基于信息熵的約簡算法

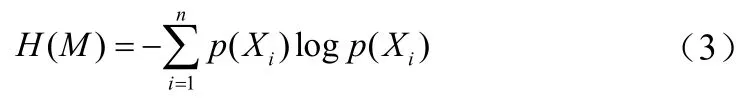
屬性集M相對于屬性集K的條件熵H(K｜M)為：

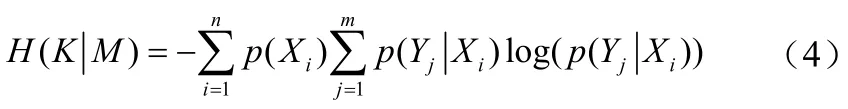
屬性集M同屬性集K的互信息為：

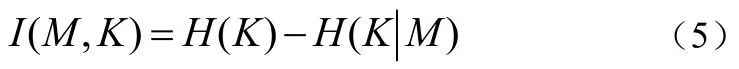
基于信息熵的約簡算法流程為：

步驟1：針對決策表S=(U,C∪D,V,f )，計算決策屬性D的信息熵H(D)；

步驟2：計算條件屬性C同決策屬性D的互信息量I(C,D)；

步驟3：求核屬性。初始化core=?，對?a∈C，有f(x, D)≠f(y,D)，且f(x,C-a)= f(y,C-a)，屬性a就為決策表的核屬性；

步驟4：令R等于核屬性，并計算R同決策屬性D的互信息量I(R, D)；

步驟5：對?a∈C-R，計算其同決策屬性D的互信息量I(a, D)，找出使互信息量最大的屬性a，且R=R∪{a}；

步驟6：計算此時屬性R同決策屬性D的互信息量I(R,D)，判斷屬性R的信息量和條件屬性C的信息量是否相等，如果是就停止運算；否則轉至步驟5。

1.2基于可辨識矩陣的約簡算法

基于可辨識矩陣約簡算法的流程為：

步驟1：針對知識表達系統S=(U, C∪D,V,f )，C為條件屬性，D為決策屬性，a(x)、D(x)為第x條記錄對應屬性的值。建立決策表的可辨識矩陣M=(mij)n×n。(mij)n×n有如下定義[6]：

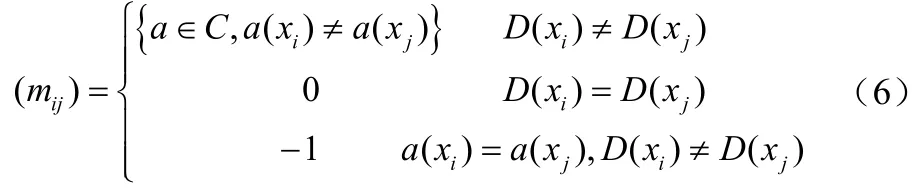
其中i,j=1,2,…,n。

步驟2：如果M=(mij)n×n中存在單屬性元素，則將其歸入集合R，集合R就稱為核屬性，并轉至步驟4，否則建立可辨識矩陣中非零元素的析取表達式：

其中ai為非零元素mij中的屬性項。

步驟3：對任意Ri=R(i=1, 2, …, n)，如果Ri∈M，則令M中與Ri對應元素等于0，得到新的矩陣M′。對新矩陣M′中的所有非零元素建立析取表達式：

ai為非零元素mij中的屬性項。

步驟4：將析取表達式進行合取運算，得到合取范式為：

步驟5：將合取范式L轉換為析取范式：

步驟6：將核屬性R中的屬性插入L′中的每個析取范式中，得到的每一組集合就為一個屬性約簡結果。基于可辨識矩陣約簡算法得到的約簡結果通常都不止一組。

1.3基于遺傳算法的約簡算法

定義2 在一個知識表達系統中，P、Q分別為論域中的屬性集合。當

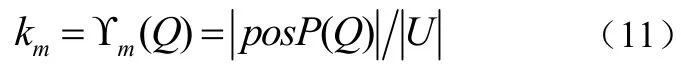
稱屬性Q是km度依賴于屬性P的，︱·︱表示屬性集合中包含對象個數。

定義3 令屬性子集PP′?，則P′關于Q的重要性定義為：

特別的，當P′={a}時，屬性a∈P關于Q的重要性定義為：

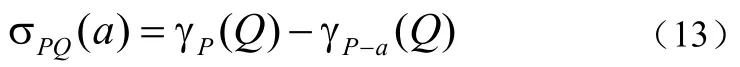
定義4 適值函數是在遺傳算法中評價個體位串適應性的標準，定義為[7]：

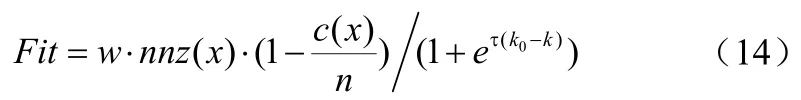
每個個體被選擇的概率可以表示為：

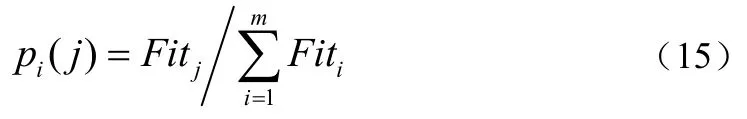
其中n表示條件屬性的數量，c(x)表示個體所含條件屬性的數量，k表示全部條件屬性相對于決策屬性的依賴度，kp為每個個體包含的條件屬性相對于決策屬性的依賴度。

根據以上定義，遺傳算法的流程為：

步驟1：知識表達系統S=(U,C∪D,V,f )，由公式(12)計算條件屬性C相對于決策屬性D的依賴度kp；

步驟3：產生n個長度為r的初始種群，個體中每一位對應一個條件屬性；

步驟4：計算每個個體所含條件屬性相對于決策屬性D的依賴度kp，并利用式(14)計算出適值最大的個體傳遞給下一代；

步驟5：對于規模為n的種群，計算其每個個體適值及被選擇的概率，得出被選擇的期望數。以輪盤賭的方式對個體進行挑選，組成新的種群；

步驟6：對種群進行交叉和變異操作，并針對于現階段的每個個體，再次計算所含條件屬性相對于決策屬性的依賴度kp和每個個體的適值；

步驟7：判斷遺傳算法是否成熟（連續n代的最優個體適值不繼續增加），如果最優個體的依賴度k=kp，且該屬性集合的具有獨立性，則停止運算，否則轉至步驟5。

1.4基于Johnson算法的約簡算法

Johnson算法是一個新型約簡算法，由用戶來決定屬性的權重，從而可以快速地計算出約簡組合[8]。選取當前頻率最大的屬性加入約簡組合，如果一個屬性出現次數的頻率越大，它的可分辨能力就越強。而且Johnson算法得出的約簡組合只有一組，相比于其他方法更加直觀。設定R表示約簡，其算法流程為：

步驟2：計算可分辨矩陣M，M={mij:mij≠?}；

步驟3：計算屬性ai在M中出現的次數ωai(M)；

步驟4：選擇使ωai(M)最大的屬性記為a，R=R∪{a}；

步驟5：將M中包含a屬性的全部刪除；

步驟6：如果M=?，停止計算，否則轉至步驟3。

2 屬性約簡方法存在問題發展趨勢

粗糙集理論的優越性在很多實際應用中得到了證明，其屬性約簡仍有一些間題有待解決。下面列舉一些今后可能的研究方向。

（1）如何提高約簡算法的效率，降低算法的執行效率和復雜度，是進一步研究粗糙集理論的關鍵部分；

（2）當屬性值不是一個固定值，而是一個連續區間時，如何將數據進行合理的離散化處理，直接從這類信息系統中獲取知識是一個值得研究的問題；

（3）屬性約簡方法眾多，在實際應用中可以互相融合，提高約簡速度。如很多方法就使用可辨識矩陣來獲取核屬性集[9]。

3 總結

本文總結了現有粗糙集屬性約簡方法，分析了現有方法的存在缺點，并提出了未來的發展趨勢。粗糙集屬性約簡方法的不斷完善對如何在大數據時代做出正確的決策具有重要的理論和現實意義。

[1] 王國胤,姚一豫,于洪.粗糙集理論與應用研究綜述[J].計算機學報,2009,32(7):1229-1246.

[2] 湯建國,祝峰,佘堃.粗糙集與其他軟計算理論結合情況研究綜述[J].計算機應用研究,2010,27(7):2404-2410.

[3] 黃楠.基于粗糙集和模糊聚類方法的屬性約簡算法[J].電腦知識與技術,2012,8(32):7718-7719.

[4] 譚旭.改進分辨矩陣下的增量式條件屬性約簡算法[J].系統工程理論與實踐,2010,30(9):1684-1694.

[5] 陳媛,楊棟.基于信息熵的屬性約簡算法及應用[J].重慶理工大學學報(自然科學),2013,27(1):42-46.

[6] Yiyu Yao, Yan Zhao. Discernibility Matrix Simplification for Constructing Attribute Reducts[J]. Information Sciences, 2009, 179(17):867-882.

[7] 顏艷,楊慧中.基于遺傳算法的粗糙集屬性約簡算法[J].計算機工程與應用,2007,43(31):156-158.

[8] 陳桂芬,馬麗,董瑋.聚類、粗糙集與決策樹的組合算法在地力評價中的應用[J].中國農業科學,2011,44(23): 4833-4840.

[9] Junbo Zhang, Tianrui Li, Da Ruan, et al. Rough Sets based Matrix Approaches with Dynamic Attribute Variation in Set-valued Information Systems[J]. International Journal of Approximate Reasoning,2012, 53(4):620-635.

A survey of rough set reduction process algorithm

Attribute reduction is most important issue in the rough set theory. This paper describes rough set reduction process algorithm based on information entropy, discernable matrix, genetic algorithms, Johnson algorithms, pointing current problems and developing tendency in rough set reduction process algorithm, motivating higher research development of rough set reduction process algorithm.

Rough set;reduction process;algorithm

O13

A

1008-1151(2015)11-0017-03

2015-10-12

廣西科學研究與技術開發計劃（桂科能1598020-8）。

唐衛國（1974－），廣西壯族自治區右江礦務局有限公司工程師，研究生學歷，碩士，研究方向為礦山通風與安全工程。

徐晉勇（1962－），男，桂林電子科技大學教授，博士，從事金屬材料表面改性、機械工程及其產業化的研究。