基于Monte Carlo法的深基坑支護結構可靠度研究

萬志輝，劉紅艷，步艷潔，張 旭

（遼寧工業大學土木建筑工程學院，遼寧 錦州121001）

基坑工程的設計與施工由傳統的以強度控制為主，轉向了今天的以變形控制為主，因此，變形控制的設計與施工顯得愈加重要［1］。對于深基坑支護結構來說，樁體水平位移是圍護結構的安全狀況重要指標，也是設計與施工的變形控制重要指標之一，因此對樁體水平位移必須進行嚴格的控制。樁體水平位移受眾多的不確定性因素影響，可以采用可靠度方法來評價深基坑支護結構的安全性。對于深基坑支護結構的可靠度研究許多學者進行了分析［2-5］。文章對隧道基坑工程樁-內撐支護結構樁體水平位移現場監測數據進行分析，采用Monte Carlo 法對深基坑支護結構樁體水平位移進行可靠度研究，結合工程實例，考慮土性參數等的隨機性和變異性特征，計算各階段支護結構的可靠度指標，用以分析深基坑支護結構安全穩定性，為深基坑工程的設計與施工提供指導性建議。

1 樁-內支撐支護結構的Monte Carlo法可靠度理論

1.1 極限狀態方程

對于樁-內支撐支護結構，當在基坑開挖面以上未架設內支撐時，支護結構繞樁底端點轉動，使其樁頂向基坑內側產生最大位移；當在基坑開挖面以上架設內支撐時，由于內支撐的作用，圍護樁體的變形逐漸轉向弓形，最大水平位移發生的部位也逐漸下移。著眼于樁體最大水平位移，對深基坑支護結構進行可靠度分析，據此建立極限狀態方程：

式中：fmax為基坑支護樁體水平位移控制值；f為樁體最大水平位移計算值。

當Z＞0時，則深基坑支護系統安全，不會發生破壞；當Z＜0時，則深基坑支護系統不安全，會發生破壞；當Z=0時，則表現為樁體水平位移計算值達到了樁體水平位移控制值，此時，深基坑系統處于極限平衡狀態，此式即為深基坑支護結構樁體水平位移可靠度分析的極限狀態方程。

1.2 可靠度指標計算與選取

Monte Carlo法確定可靠度指標β值的基本步驟如下。

1）將工程中的γ，C，φ等值產生（0，1）區間的均勻分布隨機數序列{ri} ，在此基礎上，通過反函數法將隨機數序列{ri} 轉化為相對應的γ，C，φ正態分布的隨機數，則Xi=F-1(ri)，即轉化為給定分布的隨機變量X1，X2，…，Xn。

2）設定總模擬次數N。只需模擬次數足夠大，就可以得到相當精度的結果，一般模擬次數在5 000～10 000次能滿足精度要求，為了得到較高的模擬精度，采取總模擬次數N=10 000次。

3）將產生的隨機變量代入功能函數中Z=g(X1,X2,…,Xn)進行計算，得到Z＜0的次數為L，則工程結構的失效概率與可靠度指標可由下式算得：

當隨機變量為正態分布時，可由β=-φ-1(Pf)求解相應的可靠度指標。

目前，在巖土工程中目標可靠度β0取值尚未給出明確的規定。文獻［8，9］中提出在地基承載力與地基變形可靠度計算時，目標可靠度指標分別取0.95，0.85；在深基坑支護結構抗傾覆破壞穩定可靠度計算時，目標可靠度指標取1.5；在樁錨支護結構穩定性分析計算中，基坑的安全等級為一、二級時，目標可靠度指標分別取2.5，2.0。考慮到深基坑支護工程受眾多的不確定性因素影響，為了滿足基坑支護結構的可靠性并考慮在基坑工程的經濟性，深基坑支護結構的目標可靠度指標β0取2.0，相應的失效概率Pf0為2.28%。

1.3 可靠度指標計算程序

采用Matlab語言編程，將上述Monte Carlo法計算可靠度指標的基本步驟編制成計算機程序（例如γ正態分布的隨機數編制程序：γ=normrand(Mu,Sigma,m,n)產生服從N(μ,σ2)分布的m行n列隨機數組γ），得到樁-內支撐支護結構樁體水平位移的可靠度分析計算程序，以其求失效概率Pf及相應的可靠度指標β，將得到的可靠度指標與目標可靠度指標進行比較，進而評價樁-內支撐支護結構的安全穩定性。程序計算流程圖如圖1所示。

圖1 程序計算流程圖Fig 1 The program flow chart of calculating

2 工程實例分析

2.1 工程概況

成都至都江堰新建鐵路離堆公園支線雙線隧道工程，該隧道工程是由二環路和太平街行進水文化廣場，總長度3 241 m。以DK50+490-DK50+793隧道區段明挖順作法施工為研究對象，該區段開挖深度約為13.5 m，標準寬度為12.1 m。

本區段所處區域為成都平原冰水-流水堆積地貌，土質以細砂、卵礫石層為主，根據巖土工程勘探報告提供的土體力學參數，對各參數進行統計處理，得出各主要土層分布及其力學參數指標如表1所示。該段位于人口密集、建筑高大稠密、交通擁擠的地段。另外，由于汶川地震影響，周圍建筑出現裂縫，存在危樓較多，根據本區段隧道地下管線以及工程周邊環境等綜合影響因素，確定該隧道基坑工程安全等級為二級。

表1 土層物理力學參數指標Tab 1 The soil physical and mechanical parameter

2.2 基坑支護結構及監測方案

基坑圍護結構采用鉆孔灌注排樁+內支撐的型式。采用Φ1 000@2 400鉆孔灌注排樁，混凝土強度等級為C25，主筋24Φ28，配筋率為1.9%，鉆孔灌注樁埋入深度19.5 m。在施工前對圍護結構及施工期間對主體結構采用管井降水，降水深度不應小于開挖面以下0.5 m。內支撐采用Φ609的鋼管，支撐豎向分兩道支撐，分別布置在-0.5 m，-6.5 m處，水平間距為4 m。本區段基坑地質及支護結構剖面圖如圖2（a）所示。

圍護樁樁體變形采用CX-03型測斜儀進行測試，施工之前在鉆孔灌注樁的鋼筋籠上預埋帶導槽優質PVC測斜管，本區段內圍護樁樁體側移布設監測點CX1、CX2。詳細的監測方案和監測方法可參見文獻［6］。

圖2 本區段基坑地質剖面圖及監測點布置圖Fig.2 Fig 2 The section foundation pit geological profile and the monitoring plan

2.3 監測數據分析

樁體水平位移能夠直接反映圍護結構的變形，是圍護結構的重要安全指標。現選取測斜孔CX1的監測數據進行分析研究。開挖過程中監測點CX1樁體水平位移曲線如圖2所示。基坑開挖步驟如表3所示。

圖3 施工過程監測點CX1樁體水平位移曲線Fig.3 Fig 3 The construction process of monitoring CX1 pile horizontal displacement curve

表2 基坑開挖步驟Tab.2 Excavation steps

從圖3中可知，在基坑開挖初期，由于未施加支撐，圍護樁呈懸臂狀態，最大水平位移發生在樁頂。隨著第一道支撐的施加（鋼支撐預加軸力設計值為250 kN），圍護樁體的變形由前傾型逐漸向弓形變化，樁體的最大水平位移也隨之向下，發生在4.5 m處。在基坑開挖至坑底且未架設第二道支撐后，樁體水平位移繼續增大，樁體最大水平位移發生在6 m處，但樁頂受到第一道支撐約束作用，增大速率有所減下。架設第二道支撐后，樁體水平位移應有減小趨勢，由于施工過程產生的時空效應，圍護樁體水平位移還在繼續增大，因此，基坑開挖結束后應減少基坑暴露時間，盡快進行結構施工。各工況的監測結果都明顯小于該監測項目的控制值30 mm（達到控制值的80%時，需作為預警值預警），所以該基坑工程是安全的。

3 對四種工況的樁體水平位移進行可靠度分析

考慮到基坑周邊施工堆載、來往車輛產生動載等因素，施加地表均布超載q=20 kPa，土體力學參數按前述所給出，為簡化計算，將γ，c，φ值按19.5 m范圍內的加權平均值計算，得到重度γ=21 kN·m-3，黏聚力c=3.76 kPa，內摩擦角φ=42.46°，相應的變異系數取為δr=0.1，δc=0.3，δφ=0.3。根據參考文獻［4］，假定γ，c，φ均服從正態分布，且各參數變量相互獨立。

3.1 懸臂狀態支護結構可靠度分析

基坑第一步開挖，開挖至地表下6 m且未施加架設鋼支撐，圍護樁呈懸臂狀態，最大水平位移發生在樁頂（5.75 mm）。將該基坑支護結構在土層中所受的土壓力分解成三個三角形荷載（峰值分別為q1，q2，q3），因此，基坑支護結構的樁頂水平位移分別在其作用下所產生的樁頂水平位移疊加求得，工況1懸臂支護結構土壓力分布如圖4所示。

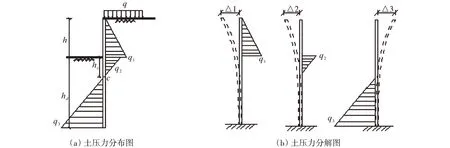
圖4 工況1懸臂支護結構土壓力分布圖Fig.4 Condition 1 cantilever distribution of earth pressure of retaining structure

可知[10]

式中：q1，q2，q3為按Rankine土壓力理論計算的土壓力強度，，h為基坑開挖深度，hd為樁體嵌入深度，hc為基坑面至樁體上土壓力零點c的距離，l為鉆孔灌注樁的總長度，分別為主、被動土壓力系數，EI為樁身抗彎剛度。參照《建筑樁基技術規范》（JGJ94-2008）［11］，對于鋼筋混凝土樁，EI=0.85EcI0=1386 MPa·m4；其中Ec為混凝土彈性模量，I0為樁身換算截面慣性矩。因此，樁頂的水平位移f=Δ1+Δ2-Δ3，則極限狀態方程Z=fmax-f=30-(Δ1+Δ2-Δ3)。

按照前述的方法，將上述公式編成Matlab語言程序，經計算得出，β=2.1419＞β0，P f=1.61%。因此，當基坑開挖至地表下6 m，未架設第一道支撐時，該工況深基坑支護結構可靠度滿足設計要求，基坑工程的安全是可以得到保證，因此，該工程基坑開挖深度與支撐架設方案是合理的，同時根據監測數據分析的結果也說明建立的可靠度分析計算程序是正確的。

3.2 單支撐支護結構可靠度分析

基坑開挖至地表下6 m并架設第一道支撐，基坑支護型式由懸臂支護結構轉化為單支撐支護結構，同時，圍護樁體的變形由前傾型逐漸向弓形變化，樁體的最大水平位移發生在4.5 m處（4.95 mm）。按工況1形式將該單支撐支護結構在土層中所受的土壓力分解成3個三角形荷載（峰值分別為q1，q2，q3）與1個鋼支撐軸力的集中荷載（Tc1），該基坑支護結構的樁體最大水平位移分別在其作用下所產生的樁體水平位移疊加求得，工況2單支撐支護結構土壓力分布如圖5所示。

圖5 工況2單支撐支護結構土壓力分布圖Fig 5 Condition 2 single support the distribution of earth pressure of retaning structure

可知［10］

同樣按照前述的方法，將上述公式編成Matlab 語言程序，經計算得出，β=2.794 4＞β0，P f=0.26%。因此，當基坑開挖至地表下6 m并施加第一道支撐時，可靠度指標大于目標可靠度指標，說明該階段深基坑支護結構可靠度滿足設計要求，基坑是安全穩定，同時此階段施工實踐也表明基坑工程是安全的。

3.3 其他工況支護結構可靠度分析

基坑開挖至坑底，未架設第二道支撐，樁體水平位移隨著開挖深度的增加繼續增大，樁體最大水平位移發生在6 m處（6.7 mm），基坑支護型式還是單支撐支護結構。基坑開挖至坑底并架設第二道支撐，由于時空效應樁體水平位移還有所增大，樁體最大水平位移發生在6 m處（8.25 mm），基坑支護型式為雙支撐支護結構。工況3和4支護結構可靠度詳述如表3所示。

表3 工況3和4支護結構可靠度分析Tab 3 The working condition of 3 and 4 retaining structure reliability analysis

同樣按照前述的方法，將各公式編成Matlab語言程序，經計算輸出結果如表4。

表4 計算輸出結果Tab.4 Calculate the output

由表可知，當基坑開挖至坑底，未架設第二道支撐時，只有第一道支撐作用的情況下，該深基坑支護結構可靠度不足，基坑不安全，此階段深基坑支護結構的失效概率大于給定的失效概率Pf0，為一個危險工況。因此，在基坑開挖至坑底后，應及時架設第二道支撐，提高基坑支護結構的穩定性，減少危險工況暴露時間，保證基坑工程的安全。當基坑開挖至坑底并架設第二道支撐時，可靠度指標大于目標可靠度指標，說明該深基坑支護結構可靠度滿足設計要求，深基坑工程是安全的，同時根據監測數據分析的結果也說明建立的Monte Carlo法深基坑支護結構樁體水平位移可靠度分析計算程序是合理、可靠的，可為今后工程技術人員提供計算依據。

4 結論

1）建立的Monte Carlo法深基坑支護結構樁體水平位移可靠度分析計算程序，運行速度快、計算精度較高，在基坑工程實踐中的可操作性強；

2）對基坑開挖施工各工況支護結構的可靠度進行了分析，分析結果與工程實際情況相符合，表明建立的樁體水平位移可靠度計算程序是合理的，同時也非常符合工程實際情況；

3）由于土性參數等的隨機性和變異性特征，采用可靠度指標作為評價深基坑支護結構的安全與否，非常符合工程實際。

[1] 張欽喜,孫家樂,劉柯.深基坑錨拉支護體系變形控制設計理論與應用[J].巖土工程學報,1999,21(2):161-165.

[2] 朱愛國,陳曉平.深基坑樁撐支護結構可靠度分析[J].建筑結構,1995(5):6-8.

[3] 楊林德,徐超.Monte Carlo模擬法與基坑變形的可靠度分析[J].巖土力學,1999,20(1):15-18.

[4] 黃艷,李惠強.懸臂支護結構可靠性分析的遺傳算法[J].華中科技大學學報,2001,29(7):106-108.

[5] 李志華,康海貴.隧道初期支護結構可靠度計算方法研究[J].武漢理工大學學報,2009,31(10):63-67.

[6] 李雷雷.基坑變形監測分析及單撐-排樁墻支護結構抗傾覆可靠度研究[D].成都:西南交通大學,2012.

[7] 黃志全,王安明,畢理毅,等.深基坑支護工程可靠度分析與數值模擬[M].鄭州:黃河水利出版社,2009.

[8] 王釗.樁—錨桿支護結構可靠度研究[D].濟南:山東科技大學,2010.

[9] 廖瑛.深基坑支護結構抗傾覆破壞穩定可靠性分析[J].工程勘察,2003(6):37-39.

[10] 浙江大學.建筑結構靜力計算實用手冊[M].北京:中國建筑工業出版社,2009.

[11] 中華人民共和國行業標準.JGJ4-2008建筑樁基技術規范[S].北京:中國建筑工業出版社,2008.