基于simulink/stateflow的列車碰撞時鉤緩系統建模

秦 舒，毛 鑫，沈 鋼

（同濟大學鐵道與城市軌道交通研究院，上海201804）

鉤緩系統作為地鐵車輛重要組成部分之一，通過它實現車輛之間的連接、傳遞和緩沖地鐵車輛運行過程中的牽引力和縱向沖擊力，其特性對列車動力學性能有著極大的影響［1-2］。緩沖器的動態特性可以通過緩沖器的位移與阻抗力的關系得到，即建立緩沖器位移與阻抗力關系圖。緩沖器的工作原理與減振器相同，它在縱向力作用下具有一定的彈性變形，同時變形過程中存在阻尼，阻尼有耗散車廂之間沖擊和振動的功能［3］。

列車防碰撞結構主要由自動車鉤、防爬器、能量吸收裝置組成，具體結構如圖1所示。當發生列車碰撞事故時，車鉤緩沖器做第一級緩沖，在其失效后防爬器做第二級緩沖，防爬器失效后由能量吸收裝置做第三級緩沖。為能夠實現結構的有序破壞，縱向梁設置了剪切鉸，當車鉤力增大到一定時，剪切鉸在力的作用下即被破壞，使前部較細的縱梁伸入后部較粗的縱梁里，實現車鉤與車體的分離［4］。

圖1 列車端部防碰撞結構Fig.1 Collision proof structure of train end

1 車鉤緩沖器研究現狀及工作特點分析

列車鉤緩系統建模是一個非常復雜的非線性問題，在早期的研究中緩沖器模型多使用簡化的模型（線性模型），后來隨著計算機技術等的發展，非線性模型在緩沖器建模中得到廣泛運用。

Peter，et al［5］使用剛度和阻尼的組合建立純線性的緩沖器模型，張瑞鵬，等［6］采用集中質量法建立剛度與阻尼組合的緩沖器模型用于研究列車縱向動力學，改進之處是考慮了由于車鉤間隙而造成的車鉤力死區。王娜，等［7］使用該模型研究了自動車鉤的剛度及阻尼系數對列車縱向動力學性能的影響；Durali，et al［8］根據緩沖器阻抗特性曲線，使用片段線性化模型模擬緩沖器；張鎖懷，等［9］將阻尼力簡化為阻尼系數和速度的函數，建立了非線性的緩沖器模型。類似地，魏偉，等［10］用函數的方法來描述緩沖器特性：

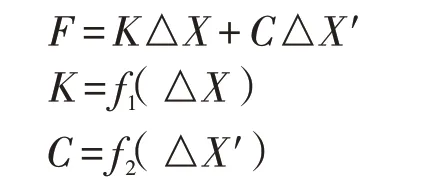
式中：F為車鉤力；△X為相對位移；△X′為相對速度。然后根據緩沖器實驗曲線，經過大量的數值分析，確定f1和f2函數，最終建立緩沖器模型。

Duncan和Webb［11］于1989年提出具有遲滯特性的緩沖器模型，它包括了前面提到了間隙特性，近似阻抗特性以及壓死后的沖擊特性。在后期的緩沖器研究中關于非線性遲滯特性的緩沖器模型有不同的數學表達，但基本原理仍與Duncan 和Webb 提出的模型類似。黃運華，等［12］探求重載列車使用的緩沖器特性，建立了多種不同特性的非線性遲滯特性緩沖器模型；常崇義，等［13］通過描述懸掛系統中懸掛力的數學方程模擬了鋼摩擦緩沖器的干摩擦阻尼遲滯特性，同時通過大量緩沖器的沖擊實驗結果擬合出緩沖器的動態特性曲線的加載曲線，進而建立了鋼摩擦緩沖器數值模型。

通過對車鉤緩沖器的運動過程分析，知其運動是由有限的幾個狀態按一定的條件轉換，循環進行的。因此解決狀態的轉換是此類仿真的關鍵，在simulink仿真環境下的stateflow，能夠方便地實現這種復雜的邏輯系統建模和仿真。stateflow 是有限狀態的圖形實現工具，它生成的監控邏輯通過Input 和Output 口可以直接嵌入到simulink模型下，從而實現二者的無縫連接，使用戶可以用圖形化的工具來實現各個狀態之間的轉換［14-15］。

當車鉤緩沖器作一級緩沖時，存在彈性壓縮、彈性伸展兩個狀態；當防爬器作第二級緩沖時存在剪切變形、塑性壓縮和防爬器壓潰3個狀態；當由能量吸收裝置作三級緩沖時存在塑性壓縮和壓潰兩個狀態。

基于上述理論可將緩沖器特性曲線分為以下幾段：①彈性壓縮；②彈性伸展；③剪切變形階段及防爬器塑性壓縮；④壓潰；⑤車體能量吸收裝置塑性壓縮。

2 緩沖器特性曲線復雜邏輯關系建立

假設緩沖器的行程為L0；變形過程中緩沖器的位移為x；變形過程中緩沖器所達到的最大位移為xmax；車鉤開始脫落時緩沖器的位移為L1；緩沖器的速度為v；車鉤力為F，其中F由x，xmax，v唯一確定，即F=f（x，v，xmax）。

1）彈性壓縮階段。此時v＞0，緩沖器特性曲線為一曲線，可通過數值分析的方法插值求得不同x時的車鉤力。

2）彈性伸展階段。此時v＜0，緩沖器特性曲線為一曲線，可通過數值分析的方法插值求得不同x時的車鉤力。

3）塑性壓縮及剪切變形階段。當彈性壓縮階段至緩沖器行程L0時，隨著力的增加進入塑形壓縮階段，當v＞0且x＞xmax時處于塑性壓縮狀態；v＞0且xmax不變時處于壓縮已壓潰部分的狀態，車鉤力不變。此時緩沖器特性曲線為平行于位移軸的直線，可求得不同x時的車鉤力。

4）防爬器壓潰階段。v＞0且x＞xmax時處于壓縮狀態；v＞0且xmax不變時處于壓縮已壓潰部分的狀態，車鉤力不變。此時緩沖器特性曲線為平行于位移軸的直線，可求得不同x時的車鉤力。

5）車體能量吸收裝置。v＞0且x＞xmax時處于壓縮狀態；v＞0且xmax不變時處于壓縮已壓潰部分的狀態，車鉤力不變。此時緩沖器特性曲線為平行于位移軸的直線，可求得不同x時的車鉤力。

所有納入對象平均年齡為（61.6±10.0）年。按年齡分組，分為＜50歲、50～60歲、60～70歲、≥70歲，其肺功能指標FEV1%為54.6%±22.7%、57.3%±22.7%、51.8%±21.5%、51.7%±17.4%，組間有統計學差異（F=3.04，P=0.028）。

根據上述邏輯關系可建立圖2所示的stateflow狀態機圖。

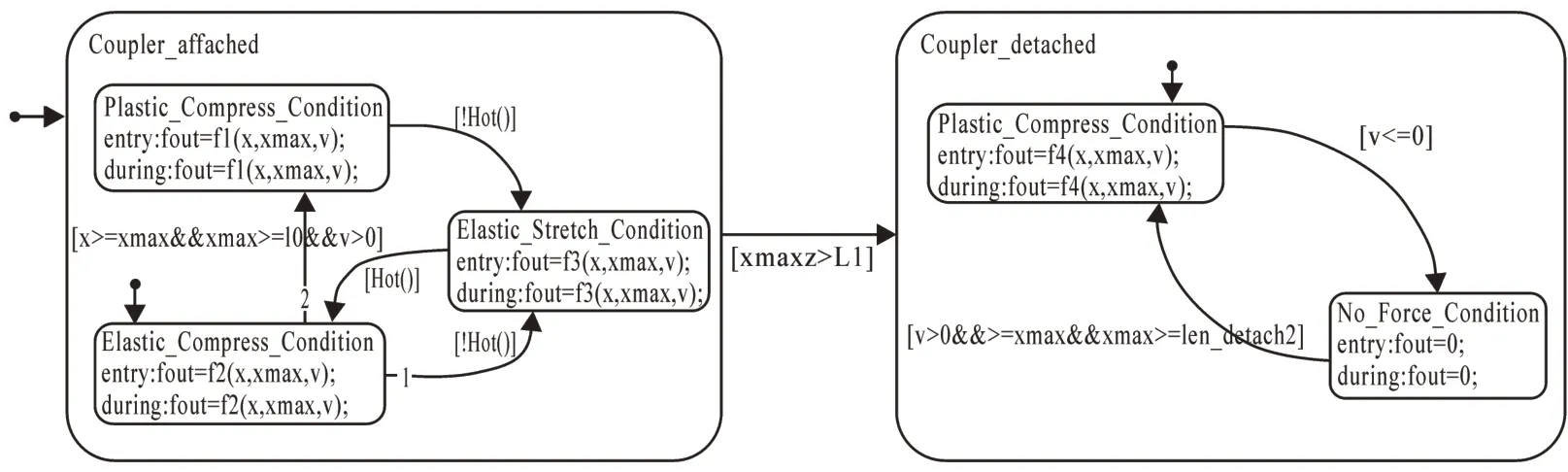
圖2 車鉤緩沖器stateflow狀態機圖Fig.2 The state machine diagram of coupling buffer

將上述狀態機圖作為模塊然后利用simulink 建立基于simulink/stateflow 的車鉤緩沖器模型如圖3所示。

3 仿真模型驗證

為了更好地分析緩沖器的特性曲線，以半自動車鉤（氣液緩沖器）為例，根據其標準參數（該緩沖器的參數設置如表1所示）編程繪制了該緩沖器的靜態特性曲線，如圖4所示。

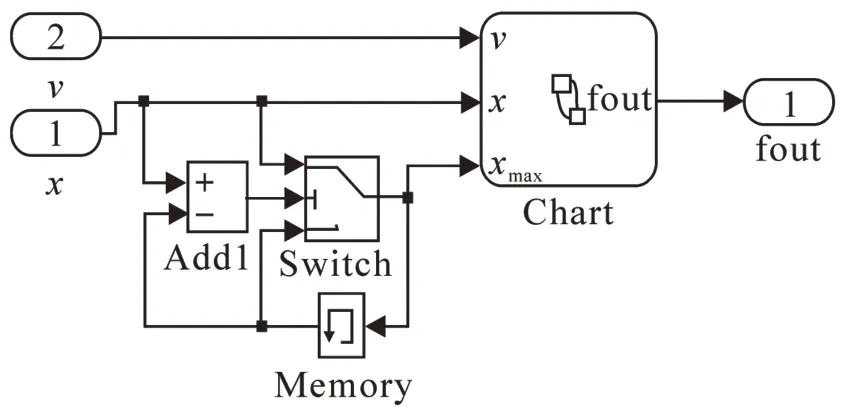
圖3 simulink系統仿真圖Fig.3 Simulink system simulation diagram

表1 半自動車鉤（氣液程緩沖器）Tab.1 Semi automatic coupler（gas-liquid history buffer）

由圖4的靜態特性曲線，可以看出車鉤緩沖器的吸能緩沖過程包括彈性拉伸、彈性壓縮、塑性壓縮以及壓潰時無力作用這幾個狀態，圖4中曲線2 為彈性拉伸、曲線1 為彈性壓縮、位移在0.28～0.35 間的線段3 為塑性壓縮及剪切變形階段（塑性壓縮至無法變形才會發生剪切螺栓被剪斷，產生剪切變形）、位移在≥0.42 mm的線段4為防爬器及車體壓潰階段，基本上符合前述的緩沖器邏輯建模分析的5個階段。

為驗證所建緩沖器模型的合理性，以兩節列車碰撞為例，選取了相應的緩沖器標準參數建立了兩節車碰撞模型進行仿真分析［16］。前車靜止在軌道上，施以停車制動，制動摩擦系數為0.15，后列車以一定的速度撞擊前車。兩節車的縱向動力學模型如圖5所示。

圖4 緩沖器靜態特性曲線Fig.4 Buffer static characteristic curve

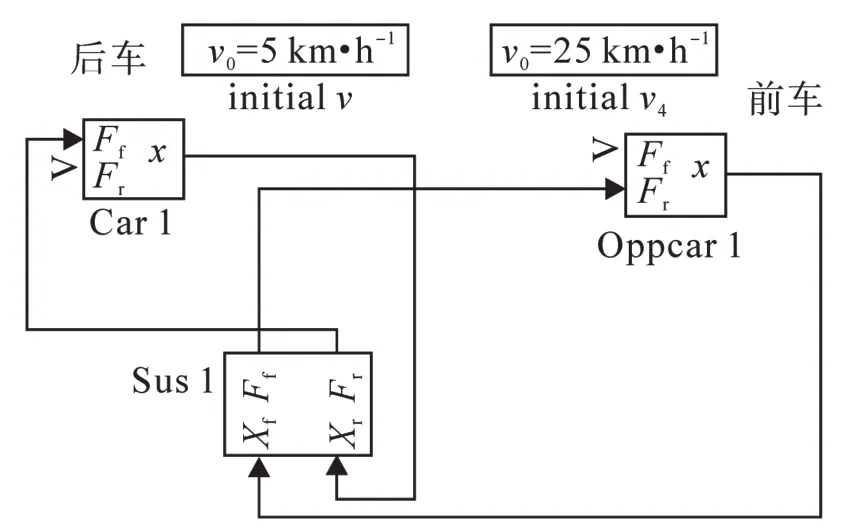
圖5 兩節車碰撞縱向動力學模型Fig.5 Two car collision longitudinal dynamics model

當后車以v0=5 km·h-1撞擊前車時，仿真結果如圖6所示。

圖6 后車的位移_時間曲線、緩沖器吸收能量曲線和車輛間作用力曲線Fig.6 The displacement time curve,energy absorbing curve and force of the rear vehicle

圖6中F1為車輛間的作用力，W1為緩沖器吸收的能量。

由圖6可以看到，當撞擊速度為5 km·h-1時，緩沖器的最大壓縮量為0.085 m，車輛間的最大作用力沒有超過500 000 N，遠小于車鉤緩沖器的剪切強度1 250 000 N，緩沖器在很短的時間內吸收了2 000 J左右的能量，此時僅由緩沖器吸收能量，剪切螺栓未被剪壞。

當后車以v0=25 km·h-1撞擊前車時，仿真結果如圖7所示。

圖7 后車的位移_時間曲線、緩沖器吸收能量曲線和車輛間作用力曲線Fig.7 The displacement time curve,energy absorbing curve and force of the rear vehicle

由圖7可以看到當撞擊速度為25 km·h-1時，緩沖器的最大壓縮量為0.465 m，車輛間的最大作用力超過了1 400 000 N，此時車鉤緩沖器在剪切螺栓的作用下被剪切失效，撞擊力直接作用于防爬器和車體上，緩沖器和防爬器在很短的時間內吸收了500 000 J的碰撞能量。

4 結論

1）從數據驅動建模的角度出發，對鉤緩系統實際的不同狀態進行細分，摒棄了傳統觀念，提出了一種新的緩沖器建模方法，具有很好的理論意義。

2）用兩節列車碰撞的模型分析了不同撞擊速度時緩沖特性曲線、車輛受力和能量吸收情況，仿真結果符合實際情況，驗證了基于simulink/stateflow建立的鉤緩系統模型的可靠性。

3）使用simulink/stateflow 相結合的仿真方法，可以有效模擬車鉤緩沖器的工作過程，在仿真過程中可以清楚地看到狀態轉換圖之間的自動切換，符合真實工況，實現了車鉤緩沖器不同狀態的邏輯控制，對列車縱向動力學的研究具有重要意義。

[1] 孫樹磊,李芾.車輛沖擊數值模擬研究[J].西南交通大學學報,2013(6):10-13.

[2] 吳慶,羅世輝.重載電力機車鉤緩系統建模研究[J].鐵道機車車輛,2012(8):1-15.

[3] 程海濤,錢立新.長大貨物列車制動時縱向動力學模型及求解方法初探[J].鐵道車輛,1998(8):3-8.

[4] 陳大名,張澤偉.鐵路貨車新技術[M].北京:中國鐵道出版社,2004:21-43.

[5] PETER CRUBER,MOHAMED M,BAYOUML.Suboptimal control strategies for multi-locomotive powered trains transactions on automatic control[J].Train Technology,1982(3):13-15.

[6] 張瑞鵬,張有玉.鐵路車輛縱向動力學仿真建模研究[J].軍事交通學院學報,2005(3):13-18.

[7] 王娜,馬衛華.啟動車鉤的彈簧剛度和阻尼系數對列車縱向動力學的影響[J].大連交通大學學報,2010(9):12-22.

[8] MOHAMMAD DURAII,BASSBAK SHADMEHRI.Nonlinear analysis of train derailment in severe braking[J].Transactions of the ASME,2003(1):2-5.

[9] 張鎖懷,張平滿.地鐵調車作業中車鉤緩沖器沖擊特性分析[J].機械設計與研究,2010(1):12-20.

[10] 魏偉,趙連剛.兩萬噸列車縱向動力學性能預測[J].大連交通大學學報,2009(2):14-20.

[11] DUNCAN, WEBB P A.The longitudinal behavior of heavy haul trains using remote locomotives[C]//The Fourth International Heavy Haul Railway Eonfefence,Brisbane,1989.

[12] 黃運華,李芾.車輛緩沖器特性研究[M].北京:中國鐵道出版社,2005:13-27.

[13] 常崇義,王成國,馬大煒,等.2萬t組合列車縱向力計算研究[J].鐵道學報,2006(2):23-48.

[14] 徐必勇,葉興梅.基于Simulink/Stateflow的液壓沖擊器混合建模與仿真[J].建筑機械,2009(2):13-17.

[15] 陸冠東.車輛系統動力學計算方法研究[M].北京:中國鐵道出版社,2001:23-48.

[16] 吳海超.CRH3動車虛擬駕駛仿真系統的設計與實現[J].華東交通大學學報,2012,29(2):31-35,46.