地震作用下列車-橋梁空間耦合系統動力響應分析

沙 峰，姚林泉，程 曦

（蘇州大學城市軌道交通學院，江蘇 蘇州215131）

地震是一種突發的地殼劇烈運動，世界范圍內幾乎每年都要發生多次不同震級的地震，尤其最近幾年地殼運動非常活躍，而我國作為地震災情嚴重的國家，自20世紀以來，平均大約每3年就要發生2次七級以上地震［1］。地震，尤其是震級與能量較大的地震，給人的生命財產帶來嚴重的危害。對于鐵路系統而言，較大的地震發生時，巨大的地震能量會導致路面開裂、地基變形、軌道彎曲、橋梁坍塌，列車脫軌，引發安全事故。隨著我國高速鐵路的飛速發展，鐵路橋梁在線路中的比重逐年增加，地震發生時列車過橋的概率隨之變大。隨著地震烈度的增強和列車運行速度的增加，車橋耦合系統的動力響應變得愈發復雜［2］，因此，分析地震作用下車橋系統動力響應具有重要意義。

自上世紀以來，國內外許多學者對地震作用下軌道車輛在橋梁上的行車性能和橋梁的動力響應開展了大量的理論和試驗研究工作［3-5］，研究主要集中在地震作用下不同行駛速度對車橋動力響應的影響，對于不同烈度地震作用下車橋系統動力響應的研究相對較少。在輸入地面激勵時，一些研究只考慮地震波的作用，忽略了軌道隨機不平順的影響，軌道不平順引起的列車振動會隨著列車速度的提高成倍增大［6］，新近的研究表明，對地震作用下列車運行安全性分析不應忽略軌道隨機不平順的影響［7］。從目前研究現狀來看，關于地震條件下車橋動態安全性能的研究還不夠系統、深入和完善。有的局限于垂向動力學的分析［8］，有的對車輛模型和輪軌關系做了大量的簡化，對地震與列車耦合作用考慮不全面［9］，為此需要進一步開展相關方面的研究工作。

本文在前人的研究基礎上，建立了車輛-橋梁空間耦合動力學模型，在考慮地震激勵的同時，還考慮了軌道隨機不平順的影響，使激勵更加接近真實。采用新型顯式積分法［10］求解系統動力學方程，分析了不同地震烈度對車輛運行平穩性的影響，可為地震作用下鐵路橋梁的動力響應分析和車輛的運行安全分析提供參考。

1 地震作用下車輛-橋梁耦合系統分析模型

1.1 車輛空間振動分析模型

分析中，本文做如下假定：①車體、轉向架和輪對均假定為剛體；②車體、轉向架和輪對之間均作微振動；③彈簧假定為線性，阻尼按黏滯阻尼計算；④輪軌關系采用垂向密貼橫向蠕滑線性簡化模型［11］。圖1為車輛-橋梁空間耦合系統模型，車輛采用四軸整車模型，車體和轉向架考慮橫移、沉浮、側滾、搖頭和點頭5個自由度，輪對考慮橫移、沉浮和側滾3個自由度，整車共有27個自由度。

根據D′Alembert原理可以推導出車輛多剛體系統的動力學方程，可表示為如下矩陣形式，具體形式可參見文獻［10］。

式中：[Mv]，[Cv]，[Kv]分別為車輛的質量矩陣、阻尼矩陣和剛度矩陣，分別為車輛系統振動的加速度向量、速度向量和位移向量，{Fv} 為車輛系統激勵列向量。

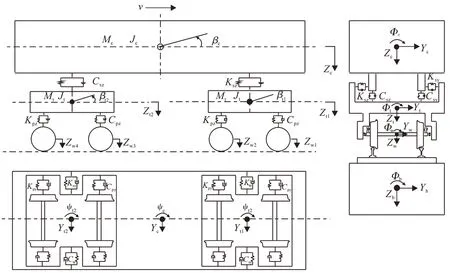
圖1 車輛-橋梁空間耦合系統模型Fig.1 Model of spatial coupled system of train and bridge

1.2 橋梁空間振動分析模型

假設橋梁為等截面簡支梁，質量均勻分布，考慮垂向、橫向和扭轉3個方向的自由度，橋梁的運動滿足小變形理論并在彈性范圍內，以垂向振動為例，其振動微分方程［12］可表示如下：

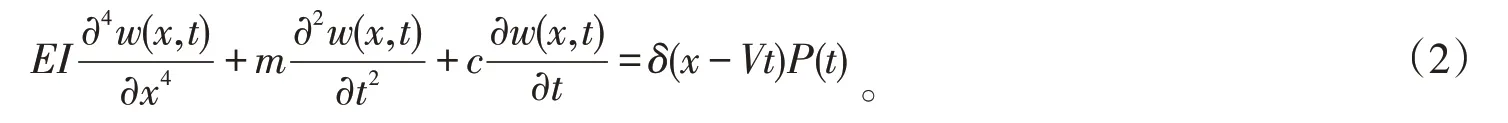
其中：δ為Dirac函數；P(t)為輪對作用在橋上的力。

對于等截面的簡支梁，其振型函數可假定為三角函數

其中：n為橋梁的模態階數。

引入廣義振型坐標qn(t)，則橋梁的任一截面上垂向的運動可由振型函數疊加表示為

采用Ritz 法，將（4）代入（2）式并乘以第n階振型函數φn(x)，再沿梁全長積分，并考慮振型的正交特性，即可將四階偏微分方程轉化為二階常微分方程：

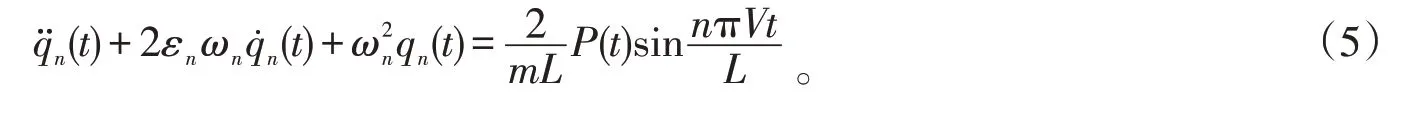
至此，得到了橋梁垂向振動微分方程。橋梁橫向和扭轉振動微分方程可類似得出［10］。

1.3 車橋耦合系統動力學分析模型

將車輛的動力學方程（1）和橋梁振型的廣義坐標方程（5）進行組合，即可得車輛-橋梁耦合系統的動力學方程：

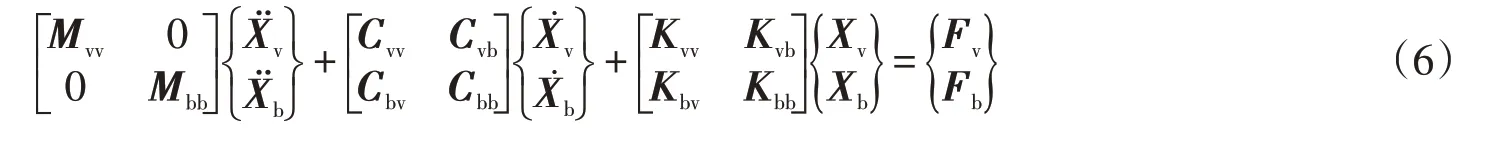
式中的下標v和b分別表示車輛和橋梁，其中

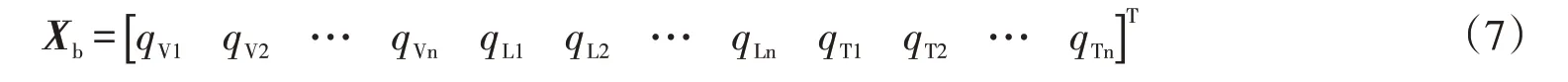
這里，qV，qL，qT分別為橋梁在垂向、橫向和扭轉方向的廣義坐標。

地震作用下車橋系統分析模型是由車輛模型和橋梁模型組成的耦合系統，系統的激勵源為軌道隨機不平順和地震的振動。地震作為外部激勵作用在車輛和橋梁上［13］。地震作用下車橋耦合系統的動力學方程為

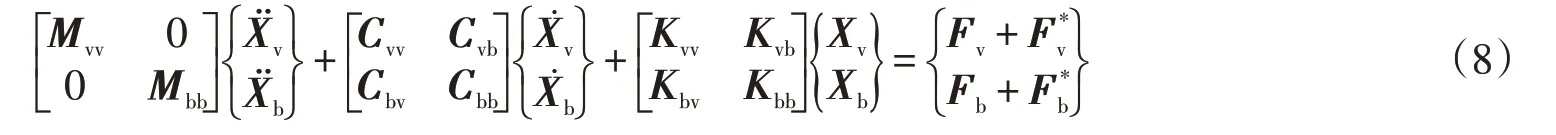
式中：Fv*，Fb*分別表示車輛和橋梁的地震力向量，篇幅所限，其它相關矩陣不詳細羅列。

2 系統激勵模型

2.1 軌道隨機不平順

軌道隨機不平順的統計特征只能依靠線路實地測量獲得，迄今為止，我國尚未形成表征自己鐵路線路狀態的軌道譜標準，只有相關部門給出的一些建議的功率譜密度表達式。而國外對于軌道不平順功率譜的研究已相當深入，并且形成了相應的軌道譜標準［10］；因此，在計算中選用了適用于高速鐵路的德國高速軌道低干擾譜，其功率譜密度公式如下：

高低不平順

方向不平順

其中：Av，Aa是粗糙度常數；Ω為軌道不平順的空間頻率；Ωc，Ωr是截斷頻率。具體取值參見文獻［10］。

通過數值模擬的方法［14］，將軌道隨機不平順功率譜密度函數轉換為空間時域樣本引入車橋耦合系統。

2.2 地震波的規格化

在分析地震作用下車輛-橋梁系統的動力響應時，通常選用一些國際上常用的真實地震加速度記錄，進行規格化處理之后作為系統的輸入激勵。地震作為外部激勵作用在車輛和橋梁上，采用一致激勵模式，假定地震發生時基礎各點以相同的振幅和相位振動，不考慮場地效應和地震波的行波效應，即每跨橋梁受到的地震作用相同。本文選用典型的El Centro地震波作為地震輸入激勵。

地震波的規格化是將實際地震記錄的加速度峰值調整為分析需要的峰值，按照《建筑抗震設計規范》［15］的規定：當結構采用三維空間模型需要雙向或三向地震波輸入時，其加速度最大值通常按1（水平1）：0.85（水平2）：0.65（豎向）的比例調整。本文在計算時不考慮車輛和橋梁的縱向振動，因此采用雙向輸入，按最不利的情況考慮，即按1（水平1）：0.65（豎向）的比例調整，地震波的加速度最大值為

式中：ay(t)，az(t)和a′y(t)，a′z(t)分別為調整前后的地震波加速度，下標y，z分別表示水平和豎向。

根據《建筑抗震設計規范》給出的地震烈度和地震加速度峰值對應關系，如表1所示，將初始地震波進行規格化處理之后即可得到分析所需的地震波，表中g為重力加速度。

表1 地震烈度和加速度峰值對應關系Tab.1 Relationship between seismic intensity and maximum acceleration

3 數值計算方法

車橋耦合系統動力學模型可知，車橋耦合系統的動力學方程可表示為如下形式：

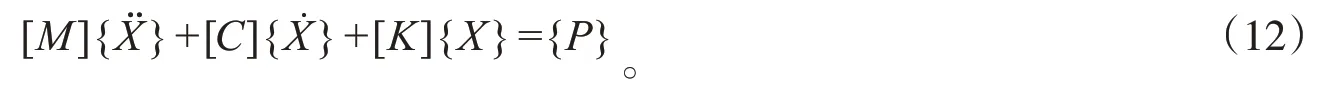
本文采用文獻[10]提出的新型顯式積分法進行數值求解。新型顯式積分法是由Newmark 法演變而來的，其積分格式為

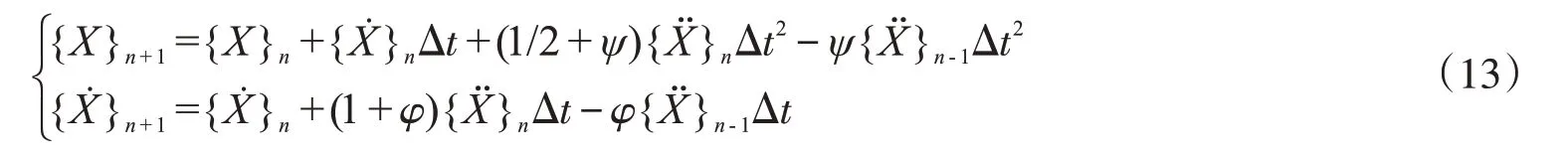
其中：φ，ψ為積分參數。將上式代入系統微分方程（12）在t=(n+1)Δt瞬時的形式

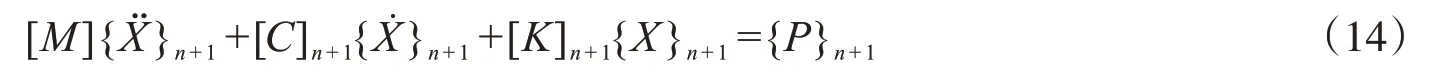
由上式可得

其中：

根據初始條件可得

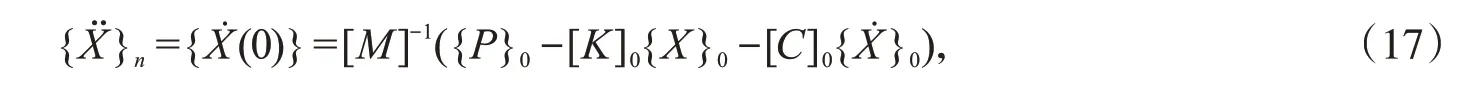
于是便可按遞推公式（13）及（15）逐次計算出各步長對應的位移、速度和加速度離散值。起步時只需令φ=ψ=0，從而使本方法具有積分“自開始”的特性。

4 車橋耦合系統動力響應分析

本文以高速鐵路車輛-橋梁耦合系統為研究對象，其中車輛選用高速車輛模型，模型的具體參數詳見文獻［10］中的附表6，橋上軌道結構和橋梁視為一體，橋梁采用多跨單線高速鐵路簡支梁形式，橋梁的相關參數為：彈性模量Eb=2.943×1010N·m-2，橋梁橫截面在兩個方向的轉動慣量分別為Ibz=8.78 m4、Iby=14.83 m4，每跨橋梁長度Lb=24 m，橋梁各階阻尼比均為0.05。假設車輛以250 km·h-1的速度勻速運行于橋梁上，橋梁共有9跨。不考慮墩高對系統響應的影響，系統的振動位移從靜平衡位置開始算起。采用新型顯式積分法求解系統振動方程，取積分參數φ=ψ=1/2，時間步長Δt=200 μs。我國將地震烈度劃分為12 個等級，6 度以下地震的加速度峰值較小，對車橋耦合系統的影響不大；橋梁的抗震設防烈度為9度，當地震烈度大于9度時橋梁可能已經發生破壞，故本文主要研究地震烈度為6～9度時車橋耦合系統的動力響應。

4.1 系統動力響應分析

根據表1不同烈度的地震所對應的加速度峰值將地震波進行規格化處理，引入車橋耦合系統，便可得到車橋耦合系統在地震作用下的動力響應，圖2～圖5為地震烈度為9度時橋梁的動力響應曲線。

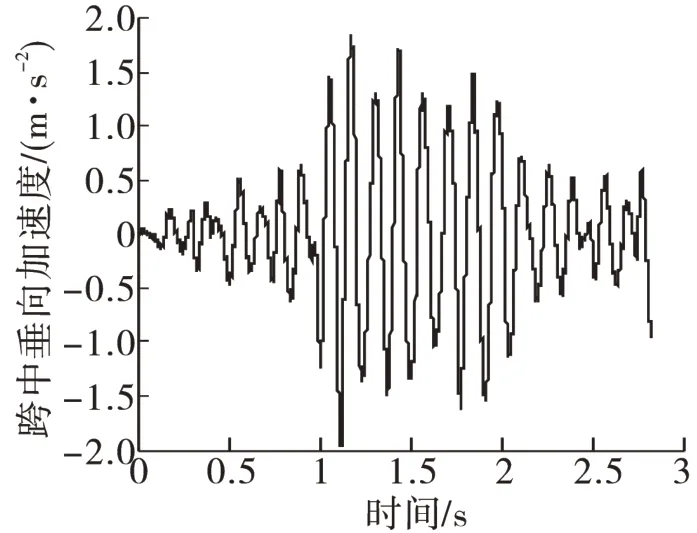
圖2 地震烈度9度時橋梁中點垂向加速度Fig.2 Vertical acceleration of the bridge midpoint under 9-degree of seismic intensity

圖3 地震烈度9度時橋梁中點橫向加速度Fig.3 Horizontal acceleration of the bridge midpoint under 9-degree of seismic intensity

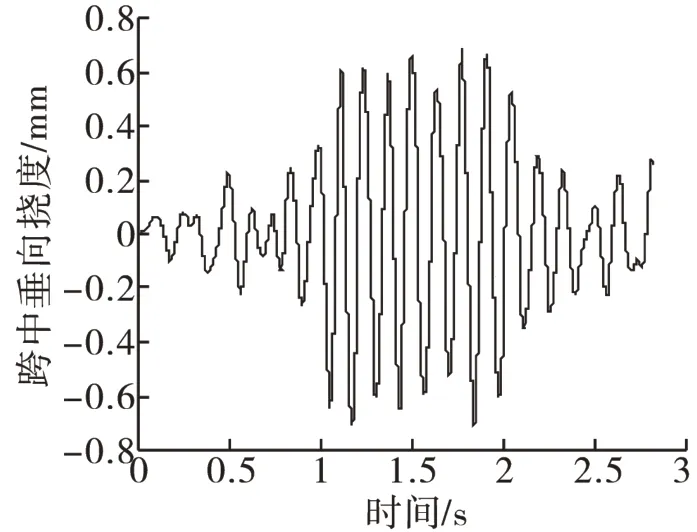
圖4 地震烈度9度時橋梁中點垂向撓度Fig.4 Vertical deflection of the bridge midpoint under 9-degree of seismic intensity

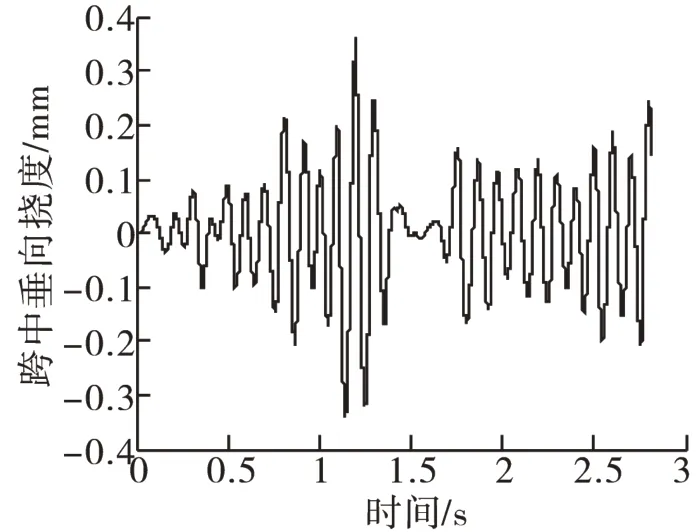
圖5 地震烈度9度時橋梁中點橫向撓度Fig.5 Horizontal deflection of the bridge midpoint under 9-degree of seismic intensity

根據《高速鐵路設計規范（試行）》［16］的規定：橋梁的垂向和橫向振動加速度限值分別為0.50g和0.14g，g為重力加速度；橋梁的垂向撓度限值為L/1 400，橫向撓度限值為L/4 000，L為橋梁跨度。由圖2～圖5可以看出：當地震烈度為9度時，橋梁垂向、橫向的加速度和撓度均滿足限值的要求。

對于高速鐵路車輛，車體振動加速度的標準為：垂向振動加速度0.13g，橫向振動加速度0.10g。表2為不同烈度地震作用下車體的振動加速度峰值，可以看出：當地震烈度為7度，地震加速度峰值為0.10g時，車輛的垂向和橫向最大加速度的絕對值分別為0.23g和0.13g，已經大于車體振動加速度標準規定的0.13g和0.10g，車輛將不能平穩地運行于橋梁之上。

4.2 地震對車輛Sperling指標的影響

我國機車車輛運行平穩性指標采用Sperling指標，平穩性評定等級的限值為3.0［10］，Sperling指標計算公式為

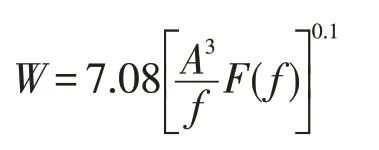
式中：A為車體振動加速度；f為振動頻率；F(f)為頻率修正系數。具體取值參見文獻［10］。

表2 不同烈度地震下車體振動加速度峰值Tab.2 Maximum acceleration of the vehicle under different degrees of seismic intensity

表3為不同烈度地震作用下車輛垂向和橫向Sperling指標，可以看出：當地震烈度為8度，地震加速度峰值為0.3g時，車輛垂向Sperling 指標超出限值；當地震烈度為9 度，地震加速度峰值為0.4g時，車輛橫向Sperling指標超出限值。

表3 不同烈度地震下車輛Sperling指標Tab.3 Sperling index of the vehicle under different degrees of seismic intensity

4.3 軌道隨機不平順的影響

為了考察軌道隨機不平順對地震作用下車橋耦合系統的影響，在一定烈度的地震作用下，對比不考慮隨機不平順和考慮隨機不平順情況下車橋耦合系統的動力響應。根據數值結果可知，軌道隨機不平順對車輛的垂向和橫向加速度響應影響都非常小，對橋梁橫向加速度響應的影響也不太明顯，而對橋梁垂向加速度響應的影響相對明顯。表4為不同烈度地震下橋梁垂向振動加速度的峰值，可以看出，隨著地震烈度的增大，軌道隨機不平順對橋梁垂向振動加速度峰值的影響越來越小。因此，在相對較弱的地震作用下，如需詳細研究橋梁的動力響應，需要考慮軌道隨機不平順的影響。

表4 不同烈度地震下橋梁垂向振動加速度峰值（m·s-2）Tab.4 Maximum vertical acceleration of the bridge under different degrees of seismic intensity

綜上可知，車輛在地震烈度為7度時已經不能平穩地運行于橋梁上。車輛運行平穩性的Sperling指標相對加速度指標較為寬松，為了安全起見，采用相對保守的加速度指標更為合理。在相對較弱的地震作用下，軌道隨機不平順對橋梁的垂向加速度響應影響明顯，分析時需要加以考慮。

5 結論

本文建立了車輛-橋梁耦合系統動力學模型，將規格化的地震波作為外界激勵引入系統模型，同時考慮了軌道隨機不平順的影響，采用新型顯式積分法對系統動力學方程進行求解，得到了車橋耦合系統在地震波和軌道隨機不平順共同作用下的動力響應，并且對不同烈度地震作用下車橋耦合系統的動力響應進行了分析。研究表明：

1）當地震烈度為9度及以下，地震加速度峰值不大于0.4g時，橋梁的垂向和橫向振動加速度，垂向和橫向撓度均滿足《高速鐵路設計規范（試行）》中規定的限值要求。

2）當地震烈度為7度，地震加速度峰值為0.10g時，車輛的垂向和橫向加速度超出限值；當地震烈度為8度，地震加速度峰值為0.3g時，車輛運行平穩性的Sperling指標超出限值。

3）車輛運行平穩性的Sperling指標相對加速度指標較為寬松，為了安全起見，應當采用相對保守的加速度指標，當地震烈度為7度，地震加速度峰值為0.10g時，車輛已經不能平穩地運行于橋梁上。

4）在相對較弱的地震作用下，軌道隨機不平順對橋梁垂向加速度響應的影響明顯，如需詳細研究橋梁的動力響應，應當考慮軌道隨機不平順的影響。

[1]王開云,王少林,楊久川,等.地震環境下鐵路輪軌動態安全性能及脫軌研究進展[J].地震工程與工程振動,2012,32(6):82-94.

[2]王少林,翟婉明.地震作用下高速列車-線路-橋梁系統動力響應[J].西南交通大學學報,2011,46(1):56-62.

[3]JU S H.Improvement of bridge structures to increase the safety of moving trains during earthquakes [J].Engineering Structures,2013,56:1563-1579.

[4]XIA C Y, XIA H, ROECK G De.Dynamic response of a train-bridge system under collision loads and running safety evaluation of high-speed trains[J].Computers and Structures,2014,140:23-28.

[5]陳水生,黃里.雙柱式橋墩剛度對橋梁地震響應分析[J].華東交通大學學報,2014,31(3):29-34.

[6]房建,雷曉燕,練松良.軌道不平順波長對橋上CRTS II 型板式軌道振動特性的影響[J].華東交通大學學報,2014,31(1):1-6.

[7]徐鵬.列車-軌道-路基耦合振動及地震條件下行車安全性分析[D].成都:西南交通大學,2012.

[8]LIU M F,CHANG T P,ZENG D Y.The interactive vibration behavior in a suspension bridge system under moving vehicle loads and vertical seismic excitations[J].Applied Mathematical Modelling,2011,35:398-411.

[9]陳令坤.地震作用下高速鐵路列車-無砟軌道-橋梁系統動力響應及走行安全研究[D].長沙:中南大學,2012.

[10]翟婉明.車輛-軌道耦合動力學[M].3版.北京:科學出版社,2007.

[11]杜憲亭.強地震作用下大跨度橋梁空間動力效應及列車運行安全研究[D].北京:北京交通大學,2011.

[12]夏禾,張楠.車輛與結構動力相互作用[M].2版.北京:科學出版社,2005.

[13]張楠,夏禾.地震對多跨簡支梁橋上列車運行安全的影響[J].世界地震工程,2001,17(4):93-99.

[14]陳果,翟婉明.鐵路軌道不平順隨機過程的數值模擬[J].西南交通大學學報,1999,34(2):138-142.

[15]中華人民共和國住房和城鄉建設部.GB 50011-2010.建筑抗震設計規范[S].北京:中國建筑工業出版社,2010.

[16]中華人民共和國鐵道部.TB 10020-2009.高速鐵路設計規范(試行)[S].北京:中華人民共和國鐵道部,2009.