通過“開放式習題”和“動手操作”培養學生創造性思維

河北省定州市西關東街小學 張建欣

通過“開放式習題”和“動手操作”培養學生創造性思維

河北省定州市西關東街小學 張建欣

小學數學教學通過“習題設計”和“動手操作”可以培養學生的創造性思維。創造思維的特征有：別出心裁，新奇獨特，突破常規或幾方面兼而有之。

實驗技能 興趣 物理學習

素質教育的核心是創新教育，而創新教育表現在課堂中是培養學生的創造力。教學思想中，最可貴的品質是創造性思維，而培養創造性思維則是當前全世界范圍內正在探索和研究的一個重要問題。那么，教師應如何培養學生的創造性思維呢？

一、精心設計開放式習題，培養學生的創造性思維

習慣性的、公式化的單一角度常常束縛思維的開拓，造成解題悟性形成桎梏。顯然，轉換角度尤為重要，角度轉換可以翻新出多形態的數學信息，創設多元化的思維環境，接通多方位的釋疑思路，在“橫看成嶺側成峰，遠近高低各不同”的美妙境界中頓悟題解的精髓和實質。因此，筆者習慣設計一些開放式習題，培養學生的創造性思維。

開放性習題可以使學生的思維打破常規、從事物的不同角度、不同方面進行分析，最終求得合理和正確的答案。這種練習能夠避免學生形成思維定式，是訓練學生創造性思維的有效手段。

例如，教授冀教板小學數學四年級上冊《2、3、5的倍數的特征》時，筆者不只讓學生練習已知的數字是不是2、3、5的倍數，而是在此基礎上利用逆向思維突破學生的思維定式，設計以下開放式練習題：

在□里填上合適的數字，使這個數能夠滿足以下要求：

是2的倍數：1□、2□、3□、□4、5□、7□、9□、11□、12□、13□

是3的倍數：1□、2□、3□、□4、5□、7□、9□、11□、12□、13□

是5的倍數：1□、2□、3□、4□、5□、7□、9□、11□、12□、13□

同時是2和5的倍數：1□、2□、3□、4□、5□、7□、9□、11□、12□

同時是2和3的倍數：1□、2□、3□、4□、5□、7□、9□、11□、12□

同時是3和5的倍數：1□、3□、4□、6□、7□、9□、12□、13□、15□

同時是2、3、5的倍數：3□、6□、9□、12□、15□、 18□、24□、27□

這樣的習題答案既不唯一，還有很強的選擇性。要想填上合適的數字，學生要充分調動自己的主觀能動性，再一一淘汰自己設定的不合適的數字，學生的發散思維不斷提升。每填上一個合適的數字，學生就獲得一份成就感，興趣也會越來越濃。這樣，學生在做習題的過程中非智力因素（濃厚的興趣和積極的情感投入）與發散思維得以高度融合和統一，培養和強化了創造性思維。同時，學生的創新能力在兩者的良性互動中得以提高。實踐證明，根據教材內容設計開放式的例題或習題有利于培養學生的創造性思維，提高創新能力。

二、培養學生的動手操作能力，發展學生的創造性思維

教授冀教板小學數學六年級上冊《長方體和正方形》時，筆者先讓學生找一兩個長方體或正方體的小紙盒，首先觀察它是由幾個面組成的，并在每個面上分別標上：“上”“下”“前”“后”“左”“右”的字樣。然后把盒子拆開，平鋪六個相連平面，立體圖形馬上變形為平面圖形，學生再把盒子沿折痕恢復成立體的圖形——盒子。這種魔術般的變化，給學生的視覺帶來了巨大沖擊，學生在好奇心的驅使下反復操作。學生在不斷動手操作的過程中刺激了“腦力”，獲得了由平面圖形演變成立體圖形的感性認識，想象力和創造性思維在這一認識過程中得到提升。有了以上鋪墊，教師可利用一些平面展培養和訓練學生的空間想象力，以發展學生的創造性思維。如下圖：

這是正方體盒子的平面展開圖，在六個面中分別標有1、2、3、4、5、6六個數字。

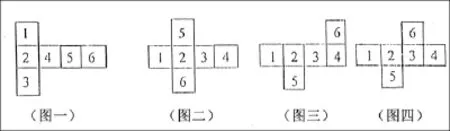
以上四幅圖要求學生通過觀察后想象，再分別說出折成小盒子后，每個正方體中，3組對面上數字分別是（）和（）

圖一相對的面分別是（）對（）、 （）對（）、 （）對（）；圖二相對的面分別是（）對（）、（）對（）、（）對（）；

圖三相對的面分別是（）對（）、（）對（）、（）對（）；圖四相對的面分別是（）對（）、（）對（）、（）對（）。

學生通過對反復操作，培養了對空間圖形的形狀、大小及位置關系的想象能力，提高了空間構圖能力，同時培養了的創新意識，為以后學習立體幾何打下良好的基礎。

總之，小學數學的重要任務就是將學生各種形式的思維盡可能向創造性思維轉化，因為思維能力是一切能力之源，豐富的基礎知識是實現轉化的必要條件。常規思維策略的積累可以產生創造性思維。教師在教學中，在學生利用常規思維獲得基礎知識的同時，更應該設計一些開放式習題刺激學生的創造性思維。教師還要善于引導學生勤于動手、動腦，培養學生的創造性思維，使學生萌生創新意識，最終達到發展學生的創造力之目的。

ISSN2095-6711/Z01-2015-12-0191