航空發動機整機靜子建模與剛度驗證

賈瑞琦，曹茂國，梁海濤

（中航工業沈陽發動機設計研究所，沈陽110015）

0 引言

在航空發動機研制、生產和使用過程中，振動問題十分突出[1]。如果要詳細地研究發動機整機的振動特性，需將轉子、機匣和支架結構等整個系統作為整體進行振動分析。目前國際上的大型航空發動機公司，如GE、PW、RR以及CIAM等均采用專門研發的整機轉子動力學計算程序，從理論上指導了新機研制、現有機型的改進和故障分析，縮短了新機型的研發周期，提高了其壽命和可靠性，改善了整機工作性能。

EJ200等先進渦扇發動機建立了用于振動監測和診斷的3維整機有限元模型。對于組成整機模型的各部件，根據其結構特點，采用了不同的分網方法[2]；Armin Schonrock等[3]利用發動機機匣殼體的靜剛度測量數據對其有限元模型參數進行了改進；張大義等[4]從計算航空發動機轉子系統動力特性的需求方面，討論了典型支承結構的徑向剛度計算中的幾個問題；高金海等[5]從計算航空發動機機匣系統動力特性需要以及有限元模型建立的角度，分析了某型渦扇發動機整機動力特性。

在整機有限元模型中，發動機機匣結構因其結構形式復雜，材料多樣以及功能差異，建模精度和方式也各有不同。需要采用不同的建模方法針對機匣自身的結構特征以及在整機靜子剛度中的貢獻程度對機匣部分進行簡化[6-10]。

本文以建立整機動力學分析模型為目標，以實際靜子結構為研究對象，對比分析了不同簡化建模方法對不同結構的影響特征。根據分析結論，建立了發動機整機靜子機匣有限元模型，并與試驗測量結果進行比較分析和驗證，為后續進行整機動力學分析提供靜子部分的有限元模型。

1 靜子結構

某型航空發動機的主承力構件包括采用整體焊接結構的進氣機匣、渦輪后機匣和整體鑄造結構的中介機匣，如圖1所示。其中主、輔安裝節分別置于中介機匣外環水平中心線兩側和加力筒體承力環水平線的一側。1號軸承座固定于進氣機匣內環，承受風扇轉子徑向和低壓轉子軸向載荷；2、3號軸承座分別固定于中介機匣內環的前后安裝邊，分別承受低壓徑向、高壓轉子軸向和部分徑向的載荷；5號軸承座固定于渦輪后機匣內環[11]。

圖1 某型發動機結構

2 結構建模時的簡化原則

由于航空技術的發展，轉子的轉速日益提高，而機匣的壁變薄，且結構大部分為回轉殼。轉子和機匣之間的聯系日趨緊密，二者之間相互耦合及影響日益加強，形成了復雜的動力特性[12]。靜子部分作為轉子的支承和傳力結構，其剛度和質量分布特征對整機轉子動力學特性具有顯著影響。

無阻尼多自由度系統自由振動的運動方程[13]為

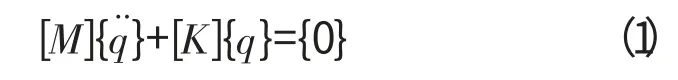
系統頻率方程為

由頻率方程可知，無阻尼系統的固有頻率主要取決于其剛度和質量，所以在簡化結構時，只要能保證前后的結構剛度和質量比值不變，且分布相似，便可以保證結構的動力特性不變。因此基本原則為（1）保證部件內部的結構力學關系不變；（2）將部件裝配成整機模型時，保證部件之間的傳力關系不變；（3）發動機整機模型狀態下的質量分布特征不變；（4）最終建立的整機模型應當保證整機的剛度和質量具有一致性。

根據航空發動機在整機狀態下的承力和傳力特點，靜子部件分為主承力機匣和其它機匣。前者是指在機匣部件中裝有軸承，直接參與向外傳遞轉子力的部件；后者是指在機匣部件中，不直接參與向外傳遞轉子力的部件。

針對主承力部件結構和受力的復雜情況，建立有限元模型時，需要保留其參與承力的所有主要結構元素，而僅對較小的倒角等結構細節進行簡化處理。整機機匣部件建模的難點在于對非承力、局部承力結構以及孔類零部件的建模處理。在對零部件進行建模分析時，在保證結構力學關系不變的前提下有必要對所分析的零部件模型進行局部簡化，減少整機系統的單元數，完成對整機模型的計算。

3 靜子部件有限元建模方法對比

靜子機匣主要為薄壁結構件，有限元建模單元主要包括殼單元和實體單元，對拉桿等桿狀部件也可以采用梁單元進行建模。不同部件的建模單元形式和簡化方法不同，需要對主承力和其它機匣部件在不同單元類型下的模型有效性和計算規模進行分析。本文以第1級風扇機匣和中介機匣模型為例，分別采用殼單元和實體單元對其建立計算模型，對比2種建模方式在不同承力或傳力功能機匣上的有限元計算特點。

3.1 風扇機匣

3.1.1 殼單元幾何模型

在殼單元建模過程中，要提取部件模型的中性面作為有限元模型網格劃分、材料選取、厚度屬性確定的幾何殼體。靜子葉片形狀十分復雜，將葉片沿徑向分成若干段，在每段的截面中提取截面的弦線，然后使用UG軟件中“通過線生成面（surface—throughcurves）”命令，將弦線和葉片的葉根和葉尖圍成的區域生成葉片曲面。對于軸向旋轉對稱件的機匣殼體，在提取中性面時，可以利用UG軟件中的“中性面（midsurface）”命令直接生成。第1級風扇靜子機匣的幾何殼體模型如圖2所示。

圖2 第1級風扇機匣殼單元幾何模型

3.1.2 實體單元幾何模型

在實體單元建模時，可直接利用已經生成的機匣實體幾何模型進行網格劃分和計算。由于工程需要，在機匣的實際幾何模型中存在各種孔洞、倒角、凸臺等，在進行實體網格劃分時需要在上述部分增加網格密度，極大地增加了劃分難度和網格數量。但是根據圣維南原理，對整個模型或整機進行動力學分析可知，上述情況對整體計算結果的影響較小。因此對計算所用的幾何實體模型進行簡化處理[14]。第1級風扇機匣3維實體幾何模型如圖3所示。

3.1.3 模型網格劃分和屬性定義

建立上述2個幾何模型后，導入計算軟件。根據計算需要定義殼體厚度、材料屬性以及部件之間的裝配聯接關系和邊界條件等物理屬性。在定義殼體模型機匣殼體厚度時，直接利用殼體對應的實體模型厚度數據。由于風扇靜子葉片形狀復雜，其厚度沿徑向不斷變化，并且葉片本身不在整機機匣傳力路線上，其主要影響機匣的質量分布狀態，定義葉片厚度時，需保證葉片質量和質心分布不發生變化，根據質量等效原則確定葉片自身的厚度。然后采用四邊形和三角形網格結合劃分。第1級風扇機匣的殼單元網格節點數、單元數和自由度分別為2438、2300、14628。采用六面體網格對實體模型進行網格劃分，第1級風扇機匣的3維實體網格節點數、單元數和自由度分別為34040、16606、251574.第1級風扇機匣2種單元網格模型如圖4所示。

圖3 第1級風扇機匣3維實體幾何模型

圖4 第1級風扇機匣網格模型

上述模型均采用鈦合金的材料數據定義屬性。對比2種機匣模型的自由模態，其位移邊界條件均為自由邊界條件。

3.1.4 計算結果對比分析

在整機傳力路線中，不是主承力部件的風扇機匣主要起傳遞轉子受力的作用，其振動特性是確定傳遞特性的基礎。實體單元和殼單元自由振動頻率對比如圖5所示。2種模型的自由振動頻率結果尤其是低階結果較為接近。

殼單元網格模型的規模要比六面體單元模型的小1個數量級以上，所占用的計算機資源更少，在多個部件模型組裝后進行整機動力學分析。因此，計算結果滿足工程精度要求時，采用殼單元可以對風扇機匣類部件進行振動模態等動力學分析。在進行整機規模的動力學計算時，在保證工程應用精度的前提下，對傳力機匣類部件采用殼單元進行分析，可以大規模縮減整個模型的數據量，減少對計算機資源的需求[15]。

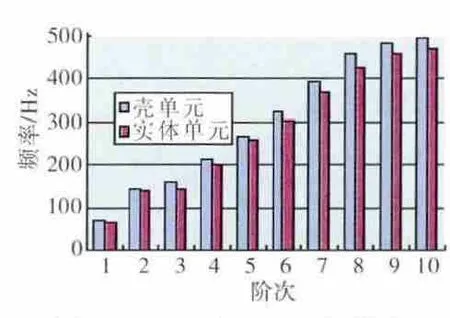
圖5 實體單元與殼單元自由振動頻率對比

3.2 中介機匣

3.2.1 建模方法

中介機匣殼單元和六面體單元建模的方法、步驟與第1級風扇機匣的相似。殼模型的片體厚度根據其對應的3維模型厚度給出。對厚度變化較大的安裝邊、軸承腔等采用等效的方式定義其厚度，即根據體積相同的原則得出。實體單元為8節點六面體網格，模型節點數、單元數和自由度分別為44606、26802和363845；采用殼單元為4節點四邊形和3節點三角形網格相結合，模型節點數、單元數和自由度分別為2906、2861和18806。相應的網格模型如圖6所示。

圖6 中介機匣網格模型

采用相同的位移邊界條件對2種機匣進行靜力學分析。在對2號軸承座施加載荷時，均采用在軸承座安裝面上施加集中力的方式。位移邊界和載荷條件如圖7所示。

3.2.2 計算結果對比分析在相同條件下，2號支點軸承座內表面平均位移對比如圖8所示。在相同受力條件下，殼單元模型計算所得的2號支點位移超出實體單元模型的，表明采用殼單元對中介機匣建模時，很大程度上降低了機匣的整體剛性。殼單元和實體單元的橫向受力變形如圖9所示。從圖中可見，在相同邊界條件和載荷下，中介機匣的支板相對其內外環在受到拉伸的同時，均有相對的轉動。中介機匣的剛性特性主要受到支板剛性以及支板和機匣殼體之間的剛度傳遞特性影響。對于中介機匣結構，其支板和機匣壁面厚度較大，尤其是支板和機匣壁面的轉接部分，已經不符合采用殼單元的薄板理論中厚度遠小于其它2個方向尺寸的基本假設，因此僅采用殼單元對中介機匣類結構建模會導致較大的計算誤差[15]。

圖7 中介機匣靜力位移邊界和載荷條件

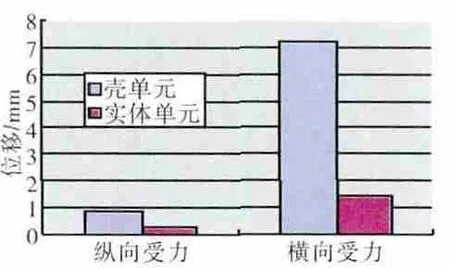
圖8 2號支點位移對比

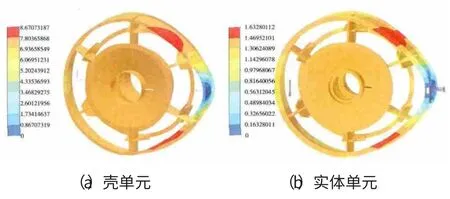
圖9 中介機匣模型橫向受力變形

通過靜力、模態對比分析得出，由于中介機匣中存在較多的安裝邊和加強結構，為了保證強度要求，大幅度增加厚度已不能較好地符合板殼理論的基本條件。部分采用殼單元時的計算誤差將會很大，甚至出現錯誤結果。

因此，對于中介機匣等發動機主要承力機匣，并不能簡單地采用殼單元建模，應采用實體單元的方式來保證計算精度。

4 靜子部件建模

針對主承力機匣結構的復雜性和進行響應分析后的結果要求，采用實體單元進行建模。對于其他機匣，為了在保證計算精度的同時盡量減少計算量，主要采用殼單元建模。各機匣都要經過仔細地幾何清理以及模型簡化甚至重新建立幾何模型后，才能導入到計算軟件中進行分網。

圖10 進氣機匣的有限元網絡模型

4.1 主承力機匣部件建模

在進氣機匣建模時，對于處在傳力路線上的結構采用了實體單元，其余的典型殼體件，且不參與軸承傳力部分采用了殼單元。進氣機匣的有限元網格模型如圖10所示。

渦輪后機匣通過8根斜拉桿與外涵承力環相連接。前者均采用梁單元進行建模。在實際部件中，與后機匣外環和外涵承力環的連接方式為鉸鏈式，各拉桿相互約束，使后機匣和外涵承力環在垂直于發動機軸向的平面內的位移相同，而對其他方向的位移并無約束。簡化處理對拉桿與后機匣外環和外涵承力環的連接方式，使拉桿與后機匣及外涵承力環鉸鏈裝配處的裝配副在沿拉桿方向的位移相等，對其他方向的位移并不添加限制。既可以保證后機匣與承力環之間通過拉桿的位移傳遞，又可以保證使2個機匣在垂直于發動機軸向的平面以外方向的位移具有獨立性。渦輪后機匣的有限元網格模型如圖11所示。

圖11 渦輪后機匣的有限元網絡模型

4.2 其他機匣部件建模

利用機匣殼單元建模方法，對風扇、高壓壓氣機、主燃燒室、高壓渦輪、低壓渦輪、加力燃燒室、收擴噴口以及復合材料外涵等機匣均建立了以殼單元為主體的有限元模型。

圖12 風扇機匣

圖13 高壓壓氣機機匣

圖14 高壓渦輪機匣

圖15 低壓渦輪機匣

圖16 燃燒室

圖17 加力燃燒室外殼、加力筒體、合流環及尾錐

圖18 尾噴口

圖19 外涵機匣

對不參與機匣的傳力，同時其葉片長度較小，自振頻率較高的靜子葉片，整級作為單個質量點處理，提取整級葉片的質量、質心、轉動慣量等屬性，采用集中質量單元的方式將整級葉片裝配到其對應的軸線位置處，集中質量單元采用“mean”單元與機匣周圍的對應位置連接，模擬其質量分布特征。相應的機匣模型分別如圖12～18所示。

以上網格劃分所得到的各機匣網格規模和材料屬性見表1。

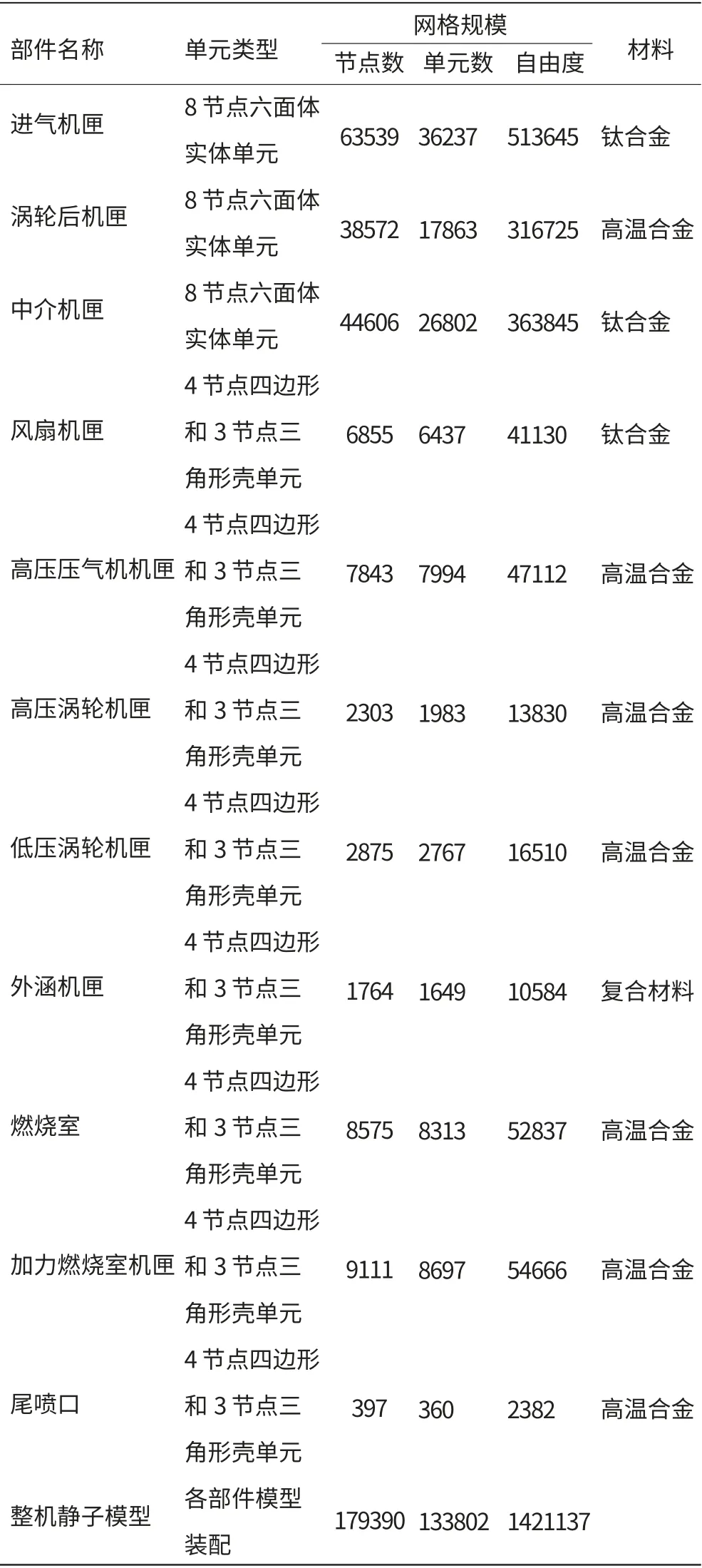
表1 靜子部件網格規模和材料

4.3 部件模型的裝配

在實際發動機部件中，各機匣部件上都留有安裝邊，2個相鄰的機匣間采用螺栓連接。由于螺栓連接時，機匣安裝邊的局部受力情況比較復雜，具有一定的非線性。對于整機規模的模型來說，局部非線性的影響范圍較小，因此在計算模型中做了簡化處理。機匣部件之間的裝配采用“點在面上”方式，即在2個進行裝配的安裝邊中的1個安裝邊節點“黏接”到另1個安裝邊的面上，可以保證連接面兩側的機匣安裝邊對應節點處的位移相同；同時不附加限制同一安裝邊上節點之間的相對位移。

4.4 整機邊界條件設定

坐標系定義為z 軸與發動機旋轉中心線重合，方向向后為正；y 軸方向向下為正；x 軸由y 軸到z 軸按右手法則確定。

根據發動機的臺架安裝方式，計算模型的位移邊界條件設置方式為中介機匣順航向看右側主安裝節處約束其沿x、y、z 方向的平動位移，左側主安裝節約束y、z 方向的平動位移，2個安裝節上均不限定其以安裝節連線方向為軸的轉動。加力筒體吊耳處約束y方向平動位移，不限定吊耳處的轉動自由度。

按照整機機匣靜柔度試驗時的加載方式，分別沿x、y 方向，在1～3、5號支點的軸承座中心面上施加10 kN的作用力，計算發動機機匣整體狀態下的變形。

機匣承力系統的有限元模型如圖20所示。

圖20 機匣承力系統有限元模型

5 計算結果

利用已建立的整機機匣有限元模型，計算了發動機整機狀態下的各支點的靜柔度，并將計算結果與試驗結果進行了對比分析。

最終計算所得的各支點相對于發動機主安裝節的靜柔度相對值見表2。

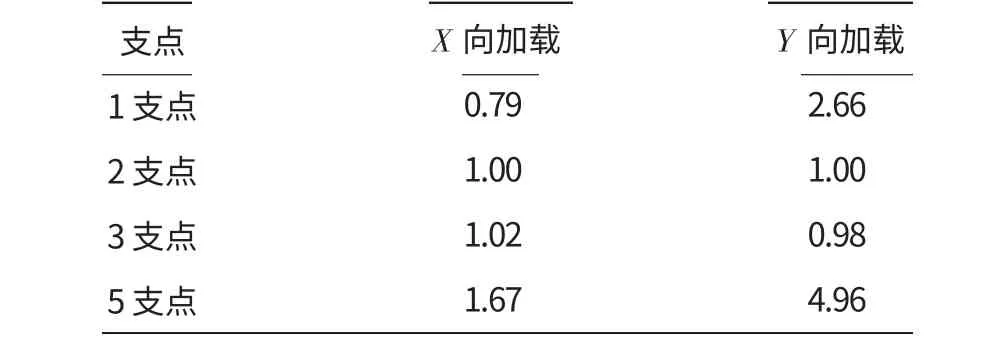
表2 各支點相對于發動機主安裝節靜柔度值

6 靜柔度試驗及結果對比

對承力系統靜柔度進行試驗，測量了承力系統1～3、5支點的靜柔度。

6.1 試驗項目及載荷

分別在某型發動機的1～3、5的軸承中截面處施加橫向力，測量軸承中截面的橫向位移，計算軸承相對于主安裝節的靜柔度。在室溫條件下，按照臺架試車要求安裝在發動機專用靜力試驗臺上進行試驗。

6.2 試驗加載方式和測量方案

1支點靜柔度試驗加載裝置（局部）如圖21所示。從圖中可見，橫向力加載螺桿1和3通過杠桿5、關節軸承和模擬軸承7對1號軸承座施加橫向載荷，測力計2、4的差值為橫向載荷。其他支點位置的加載方式與1號軸承座類似。

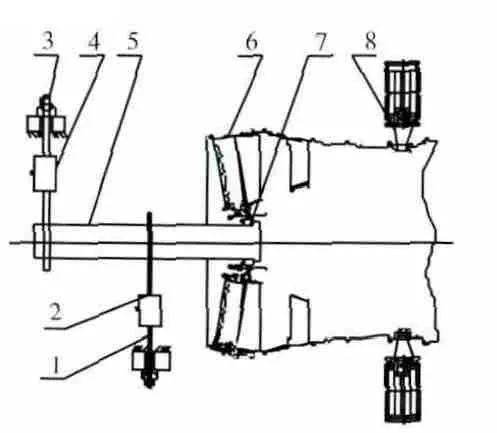
圖21 1支點靜柔度試驗加載裝置（局部）

6.3 計算結果與試驗結果

整機支點柔度計算與試驗結果見表3。

表3 整機支點柔度計算與試驗對比

從表中可見，1～3支點的柔度計算值與試驗值相對于主支點的相差較小。5支點的柔度計算值與試驗值相對于主支點的相差較大，相對誤差分別為17%（X 向）和19%（Y 向）。

5支點位于渦輪后機匣，通過在同一平面內（垂直于軸向的平面）的8根斜桿與外涵承力機匣連接。該裝配方式使5支點的徑向靜柔度特性具有較強的非線性，在試驗加載過程中也發現了該現象。在整機機匣的靜剛度計算中，模擬拉桿與機匣的裝配關系時進行了線性簡化，僅限定參與拉桿與機匣裝配處的節點位移沿拉桿方向相同，不限定裝配處節點其他方向的位移。與實際裝配關系相比，降低了機匣產生相對位移時渦輪后機匣與外涵承力機匣之間的剛性，使得5支點的柔度計算值大于試驗測量值。

7 結論

通過對比不同功能機匣建模方式，將各主要靜子部件的有限元模型組裝成整機模型，并進行了整機狀態下各支點的靜柔度計算，得到如下結論。

（1）對靜子建模可以分為主承力機匣部件和其他機匣部件分別進行。對機匣建模時，可以采用殼單元或實體單元。相同結構殼單元的網格數目比3維單元的有較大幅度地減少；

（2）主承力機匣結構比較復雜，并且直接傳遞轉子作用力。因此需要采用實體單元進行建模，保證模型的有效性。其他機匣基本為殼體類部件，受力情況也比主承力機匣的簡單，可以采用殼單元建模；

（3）發動機整機有限元模型計算與試驗得出各支點在橫、縱向的柔度值差值在工程精度范圍內。有限元模型與實際發動機的剛度分布符合較好，經過質量修正后，可以作為發動機整機振動計算中的靜子模型參與計算。

[1]李文明.新機研制中整機振動及其限制值實踐與思考[J].航空發動機，2002，（2）:22-26.LI Wenming.Engine vibration and its limit in development of new engine practice and consideration[J].Aeroengine，2002，（2）:22-26.(in Chinese)

[2]Moreno Barragan J A.Investigations into engine transient response due to internal and external dynamic excitations[R/OL].MTU Aero Engines GmbH，Engine Dynamics.[2014-05-25].http：//www.mtu.de/company/mtu-worldwide/mtu-aero-engines-polska/.

[3]Schonrock A，Dascotte E，Dufour K H.Validation of an aeroengine carcass finiteelementmodel bymeansof computational model updatingbased on static stiffness testing [R/OL].BMW Rools-Royce AeroEngines，[2014-05-25].http：//www.femtools.com/download.php?id=epf99/.

[4]張大義，母國新，洪杰.航空發動機轉子支承系統剛度計算中的幾個問題[J].戰術導彈技術，2005（2）：20-23.ZHANG Dayi，MU Guoxin，HONG Jie.Rigidity calculation methods for rotor supporting system in aeroengine[J].Tactical Missile Technology，2005（2）：20-23.(in Chinese)

[5]高金海，洪杰.航空發動機整機動力特性建模技術研究[J].戰術導彈技術，2006（2）：29-35.GAO Jinhai，HONG Jie.Study of modeling technique for dynamic characteristics of engine casing[J].Tactical Missile Technology，2006（2）：29-35.(in Chinese)

[6]陳萌，馬燕紅，劉書國，等.航空發動機整機有限元模型轉子動力學分析[J].北京航空航天大學報，2007，33（9）：1013-1016.CHEN Meng，MA Yanhong，LIU Shuguo，et al.Rotordynamic analysis of whole aero-engine models based on finite element method[J].Journal of Beijing University of Aeronautics and Astronautics，2007，33（9）：1013-1016.(in Chinese)

[7]Zang C，Schwingshackl CW，Ewins D J.Model validation for structural dynamic analysis：an approach to the sandia structural synamics challenge[J].Computer Methods in Applied Mechanics and Engineering，2008（197）：2645-2659.

[8]晏礪堂，朱梓根.結構系統動力特性分析[M].北京：北京航空航天大學出版社，1987：25-26.YAN Litang，ZHU Zigen.Dynamics analysis of structures[M].Beijing：Beihang University Press，1987：25-26.(in Chinese)

[9]晏礪堂.航空燃氣輪機振動和減振[M].北京：國防工業出版社，1991:30-31.YAN Litang.Vibration characteristics and decreasing method of aeroengine[M].Beijing：National Defense Industry Press，1991:30-31.(in Chinese)

[10]付才高.轉子動力學及整機振動[M].北京：航空工業出版社，2000：34.FU Caigao.Rotor dynamics and whole engine vibration[M].Beijing：Aviation Industry Press，2000：34.(in Chinese)

[11]劉長富，鄧明.航空發動機結構分析[M].西安：西北工業大學出版社，2006:21.LIU Changfu，DENG Ming.Structural analysis of aeroengine[M].Xi’an：Northwestern Polytechnical University Press，2006:21.(in Chinese)

[12]陳果.航空發動機整機振動耦合動力學模型及其驗證[J].航空動力學報，2012，27（2）:241-254 CHEN Guo.A coupling dynamic model for whole aeroengine vibration and its verification[J].Journal of Aerospace Power，2012，27（2）：241-254(in Chinese)

[13]鄭旭東，張連祥，劉廷毅.航空發動機整機振動特性及應變能計算與分析[J].航空發動機，2000，26（2）：42-46.ZHENG Xudong，ZHANG Lianxiang，LIU Tingyi.Whole engine vibration characteristics and strain energy analysis of aeroengine[J].Aeroengine，2000，26（2）：42-46.(in Chinese)

[14]周傳月.SAMCEF有限元分析及應用實例[M].北京：機械工業出版社，2009:35.ZHOU Chuanyue.Finite element analysis and application example of SAMCEF[M].Beijing：China Machine Press，2009:35.(in Chinese)

[15]曾攀.有限元分析及應用[M].北京：清華大學出版社，2004：76.ZENG Pan.Finite element analysis and applications[M].Beijing：Tsinghua University Press，2004：76.(in Chinese)