壓氣機靜子有限元建模簡化方法及驗證

屈美嬌，王克明，孫 陽，辛桂雨

（1.沈陽航空航天大學航空航天工程學部，沈陽110136；2.中航工業航空動力機械研究所，湖南株洲412002）

0 引言

靜子系統動力特性計算是研究航空發動機整機振動的必要途徑。國內外學者普遍采用有限元數值計算方法來獲取靜子支承動剛度[1]。靜子葉片數量多、結構復雜、形狀不規則，導致有限元計算規模大、效率低，甚至無法計算。為了快速準確地確定靜子系統的動力特性，開展壓氣機靜子葉片的有限元簡化建模方法研究具有重要意義。

有限元法是將復雜方程系統通過離散方法近似成具有有限自由度問題的數值計算方法，因此，離散后總自由度數（Degree of Freedom，DOF）是衡量有限元模型規模的標準之一[2]。對于幾何外形非常復雜的研究對象，采用有限元計算時，對單元的形式、數量要求較高，增加了有限元模型的自由度數。因此，如何通過對具有復雜幾何外形的零部件結構進行適當簡化，減少有限元模型的總自由度數，進而實現快速有效地確定航空發動機的動力特性成為研究人員關注的重要課題。Moore J等[3]采用實體單元計算了渦輪壓縮機的整機動力特性；Hong J等[4]用3維實體單元建立了航空發動機整機有限元模型；Sch?nrock A等[5]用有限元法計算并驗證了BR710的整機動力特性。但是上述研究均未提及葉片建模。航空發動機動力特性的大部分有限元計算分析用集中質量單元或直板簡化來代替真實葉片模型[6-8]，在一定程度上影響計算精度。高金海等[9]提出復雜幅板類零件簡化前后橫截面積、彎曲剛度和剪切模量均不變的簡化原則進行算例驗證，計算結果表明簡化前后誤差可控制在5%以內，但是并未給出明確算法。張力等[10]進行了大涵道比渦扇發動機低壓轉子葉片的簡化研究，采用等效圓環法，將大尺寸葉片等效為剛性圓環，在一定范圍內解決了葉片建模的問題，但該方法不適用于靜子葉片。本文針對壓氣機靜子葉片，分別提出8、6、4和2個截面等效簡化方法，將簡化前后葉片結構的振動特性進行對比分析。以實際航空發動機某級整流器為例，來驗證方法的有效性。

1 葉片模型和截面等效簡化法

1.1 葉片模型結構

壓氣機靜子葉片大多為實心薄葉片，外端常帶緣板，內端多帶內環。葉片包括具有葉型形狀的“葉身”和葉身以外的“基體”部分。葉身外形由若干規定剖面上的1組離散點確定，葉型的葉背與葉盆型線在前、后緣以圓弧、橢圓或特定曲線連接。實心葉片葉身的建模簡化如圖1所示。葉身較為平直，各截面重心連線可取為1條直線（即x 軸），沿x 向略有扭轉，葉片厚度是變化的。葉身自上而下由8個規定的葉型截面沿x 軸掃略而成。葉型截面最大厚度Cmax、弦長L 自上而下逐漸減小，中弧線最大高度h 先減小后增大，在截面5處最小。葉片用點焊的方式與整流器外環和內環連接，可視為兩端固支。葉身材料參數見表1。

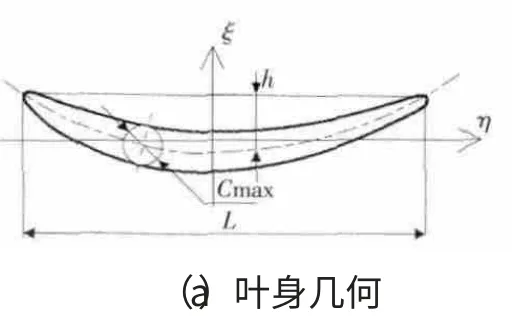
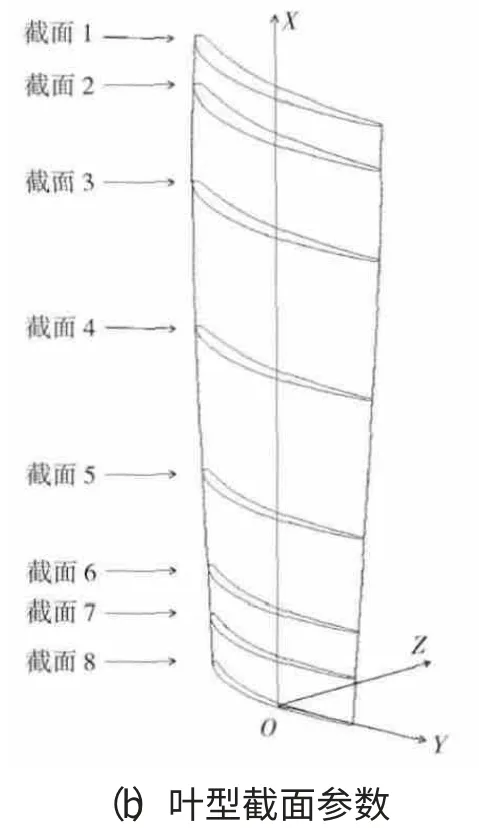
圖1 實心葉片葉身的建模簡化

表1 葉身材料參數

1.2 壓氣機典型靜子葉片受力分析

典型的壓氣機靜子葉片包括承力靜子、帶內環的整流器和懸臂靜子葉片。其中，后二者對轉子支承動剛度以及臨界轉速計算影響較大。

承力靜子葉片承受由轉子重力、轉子不平衡力、機動載荷（含陀螺力矩）和軸向力等所產生的轉子支承力所作用。在計算分析時，通常分別在葉片的內、外端加支承力和位移邊界條件，在內端的受力情況如圖2所示。從圖中可見，葉片1、5發生拉壓變形；葉片3、7發生彎曲變形；葉片2、4、6、8發生拉彎組合變形。葉片內端固定，葉身整體以彎曲和拉壓變形為主。帶內環的整流器結構與承力靜子結構相似，其葉片兩端約束形式與承力葉片的一樣，內環或外環發生形變時，葉片受力特點與承力葉片的類似，以拉壓和彎曲變形為主。

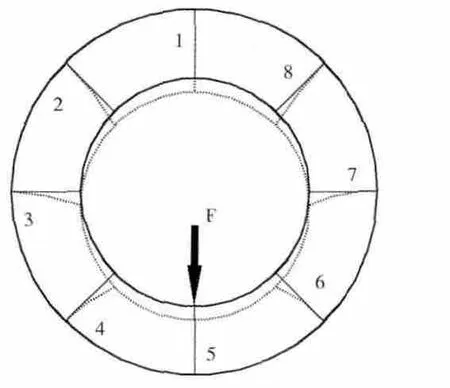
圖2 靜子承力葉片受力情況

1.3 截面等效法

從葉片受力分析可知，壓氣機靜子葉片以橫向彎曲和縱向（拉壓）形變為主。因此，為得到準確的發動機動力特性，建模時壓氣機靜子葉片應該保留本身的橫向彎曲和縱向振動特性。本文依據2種振動特征對葉片進行等效簡化及效果評價。

將實際葉片考慮為變截面梁，如圖3所示。取各截面重心連線為x 軸，設葉高為c，記葉片在坐標x處的橫截面積為A(x)，u(x，t)表示坐標為x 的截面在時刻t 的縱向位移，材料性質各向均勻，彈性模量為E，密度為ρ，變截面梁的縱向自由振動微分方程為

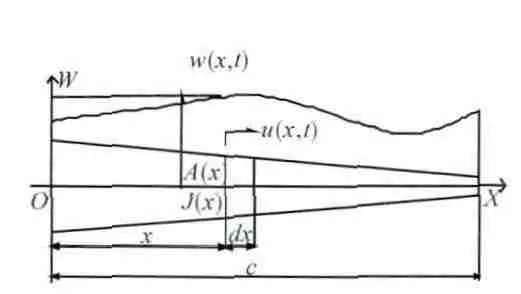
圖3 變截面梁縱向振動和彎曲振動參數

變截面梁的彎曲振動頻率通常低于其縱向振動頻率，更容易被激發。記坐標x 的截面慣性矩為J(x)，w (x，t)表示坐標x 的截面中性軸在時刻的t 橫向位移，則變截面梁的彎曲自由振動微分方程為

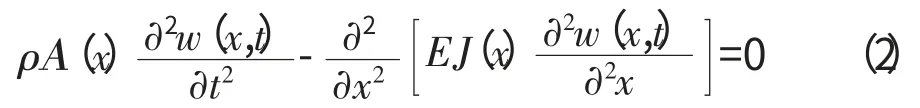
從式（1）、（2）可見，變截面梁的縱向自由振動位移只與A(x)有關，彎曲自由振動位移與A(x)和J(x)有關。因此，建立壓氣機靜子葉片有限元簡化模型要求簡化前后各截面面積A(x)和慣性矩J(x)不變。

基于上述原則，對葉片葉身實體模型進行幾何簡化。根據有限元網格劃分，葉片葉身截面采用長方形。簡化葉片模型時，需要確定的模型參數為E、ρ、c，以及長方形等效截面的截面積A′(x)、慣性矩J′(x)、長a(x)、寬b(x)。其中，已知簡化前、后模型的E、ρ、c 與簡化前模型相同；A′(x)、J′(x)、a(x)、b(x)需要通過式（3）～（6）聯立解出，通過軟件從3維模型直接提取

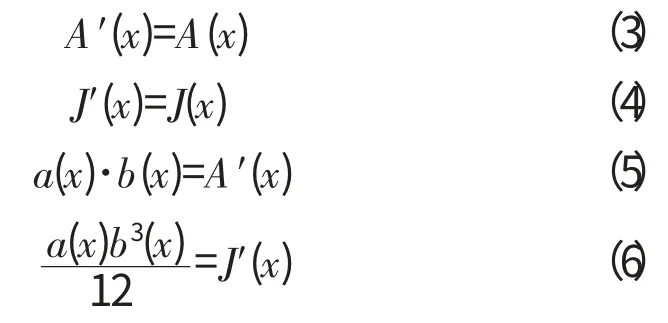
建立葉片3維幾何模型選取葉型截面1，運用CAD得出A(0)=158.00mm2，J(0)=524.26mm2。

代入式（3）~（6）為

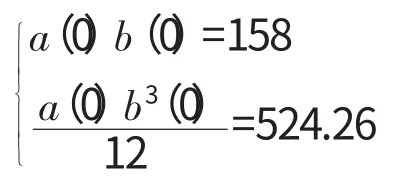
解方程組可得

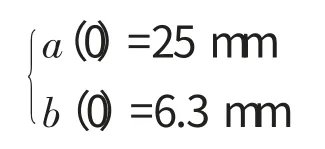
上述為葉型截面1等效長方形的尺寸。

運用3維軟件查看任意截面的參數，因此，葉身任意位置的葉型截面均可以等效。本文所取各截面均為葉身離散點所在的規定剖面，但該方法并不受此限制。經過計算得到原葉型各截面的等效截面，從截面實現整個葉片葉身的等效簡化。

2 有限元建模分析

2.1 未簡化的復雜葉片模型

基于原葉片圖紙，將8個規定剖面上的離散點輸入UG3維幾何建模軟件，運用逆向點造型方法，沿葉高方向掃掠完成幾何建模。

建立的葉片幾何模型導入Hypermesh有限元前處理軟件進行網格劃分。由于模型1結構復雜、形狀不規則，選取四面體進行網格劃分，為保證網格劃分的質量和計算精度，對曲率較大的曲面進行網格細化。將劃分好單元的有限元模型導入Ansys軟件進行模型的固有特性計算。在有限元計算中，模型規模會對計算結果產生很大影響，為排除網格對結構本身固有特性計算的影響，對模型進行了單元敏感性分析。固有頻率隨著單元數量的變化曲線如圖4所示。

從圖4中可見，在單元數大于105時，葉片前3階彎曲振動固有頻率趨于穩定，表明該規模的網格能較準確地反映該葉片結構的固有特性。本文其他模型計算都經過網格敏感性驗證。

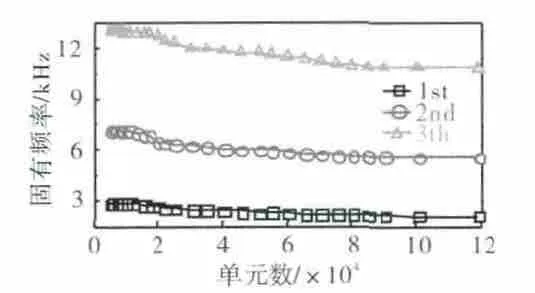
圖4 固有頻率隨單元數變化趨勢

2.2 截面等效簡化模型

在x軸各截面位置上畫出計算得到的等效長方形，沿葉高方向掃掠生成變截面梁，截面連接線為多點擬合的曲線。分別選取8、6、4和2個截面建立等效簡化幾何模型，如圖5所示。相應為模型2～5。簡化后的模型幾何形狀規整，在Hypermesh軟件中可用六面體進行單元劃分，有限元模型如圖6所示。

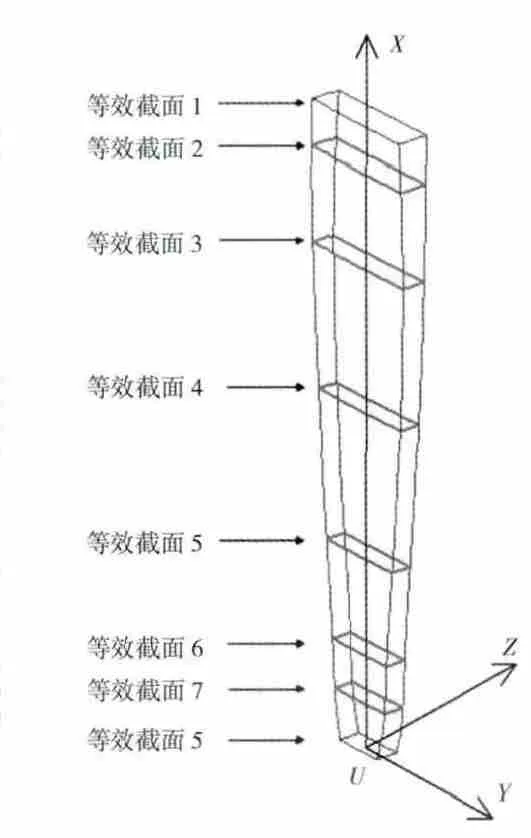
圖5 等效葉片幾何模型

圖6 有限元模型

3 模態計算結果與討論

本文分別選取前2、3階拉伸模態和彎曲模態的計算數據，對比簡化前后模型的模態振型與固有頻率，見表2。從表中可見，模型1（原模型）進氣邊厚度大于排氣邊的，彎曲小于排氣邊的。若沿x方向劃分成多個細長微元，各微元的彎曲形狀和方向都相同，可以準確識別彎曲振型。簡化后模型的各階彎曲模態振型與模型1吻合較好；同時其縱向振動振型也對應較好。

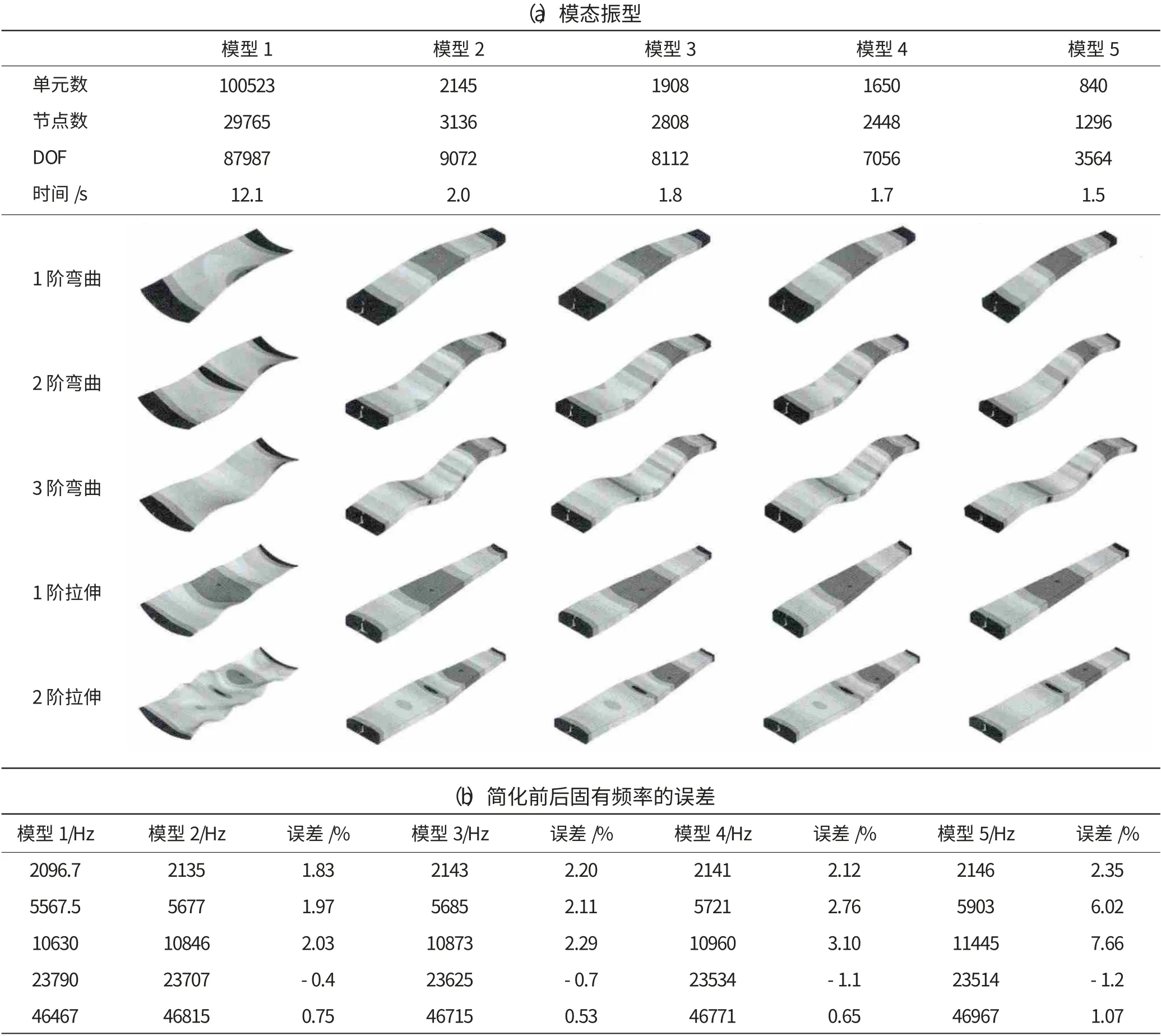
表2 葉片葉身模型模態計算結果

簡化后的模型總自由度數明顯減小。模型2～5的總自由度數分別從87987降至9072、8112、7056、3564，為模型1的10.30%、9.22%、8.02%和4.05%；在相同計算條件下CPU占用時間分別從12.1s縮短為2.0、1.8、1.7和1.5s。

模型2～4前3階彎曲振動固有頻率相對于模型1的最大誤差僅為3.1%；模型5的前3階彎曲固有頻率誤差分別2.35%、6.02%、7.66%。簡化后模型的前2階拉壓固有頻率相比原模型誤差均在3%以內，計算精度滿足要求。

4 某型航空發動機壓氣機典型整流器算例

典型整流器的結構為機匣+整流葉片+內環（或帶封嚴裝置）。本文選取某型航空發動機某級整流器對截面等效建模簡化法的正確性進行驗證。該級整流器包含垂直于發動機中軸線的靜子機匣的1個截段、1圈靜子葉片和內環。葉片以一定安裝角置于機匣，對結構采用四面體單元劃分，為模型Ⅰ，如圖7（a）所示。

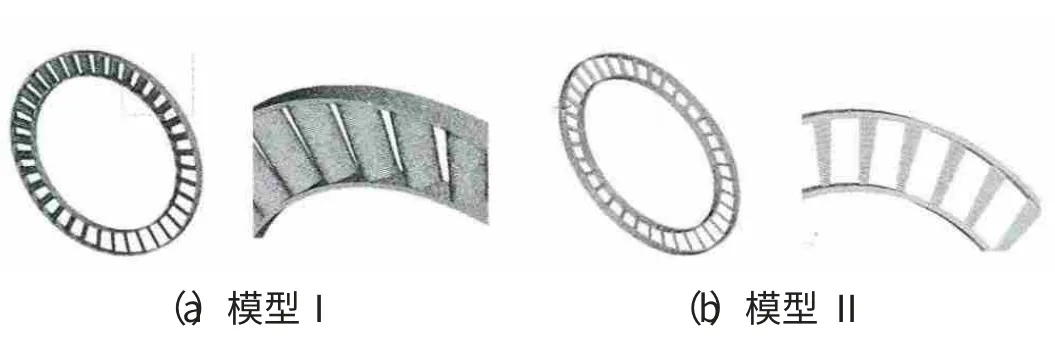
圖7 整流器有限元模型

保持模態分析參數、約束、機匣和內環結構不變，采用截面等效法建立靜子葉片的8、6、4、2截面等效簡化模型，分別為模型Ⅱ～Ⅴ簡化前、后的葉片相同的方式安裝至結構，葉片8個截面的安裝角度均不同，但差別不大，選取其平均值作為簡化后葉片的安裝角。采用六面體單元劃分網格，模型Ⅱ如圖7（b）所示，模型III～Ⅴ的網格劃分與模型Ⅱ的類似。

選取前5階模態，對比簡化前、后模型的模態振型與固有頻率，見表3。

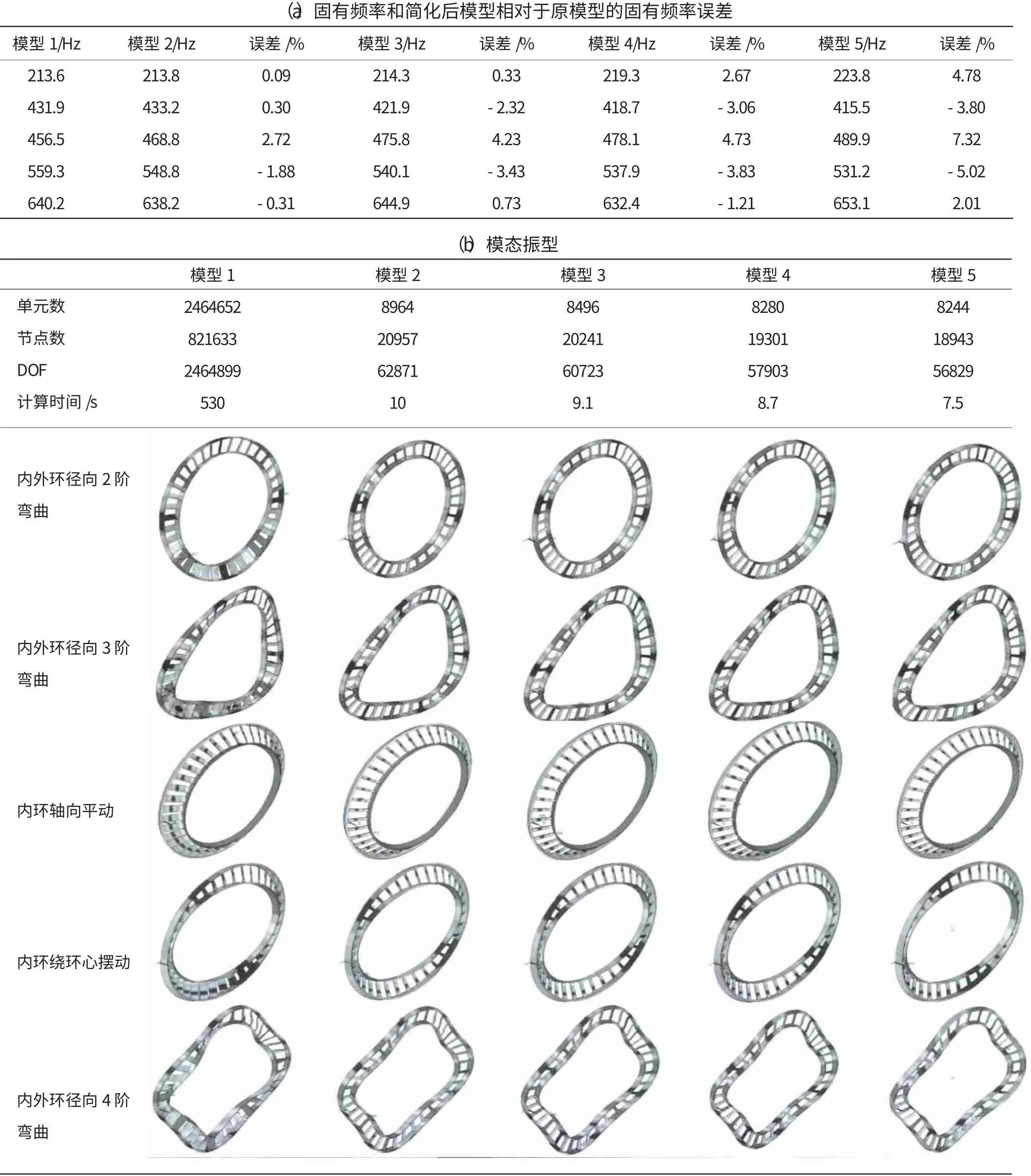
表3 整流器模型模態計算結果

（1）模型Ⅱ～Ⅴ的前5階模態振型特征與模型Ⅰ（未簡化整流器結構）的相同、形狀相似，吻合良好。

（2）簡化后的模型規模（DOF）明顯減小。模型Ⅱ～Ⅴ的總自由度數分別從2464899降為62871、60723、57903和56829，下降為原模型的2.55%、2.46%、2.35%和2.31%；在相同計算條件下，CPU占用時間分別從530s縮至10.0、9.1、8.7和7.5s，計算時間分別為原模型的1.89%、1.72%、1.65%和1.42%。

（3）模型Ⅱ～Ⅴ的前5階固有頻率計算結果與原模型最大誤差分別為2.72%、4.23%、4.73%和7.32%。

5 結論

本文針對航空發動機壓氣機靜子葉片結構復雜，整機有限元計算時模型規模過大、計算耗時過長甚至無法計算的問題，對壓氣機靜子葉片有限元建模簡化方法進行了研究。

（1）8、6、4截面等效簡化前、后，葉片模型的前2、3階拉伸、彎曲固有頻率相比，計算誤差均在3.1%以內，模型總自由度數分別減至10.30%、9.22%和8.02%，計算時間縮至16.5%、14.9%和14.1%；2截面等效簡化葉片固有頻率誤差最大為7.66%，DOF、計算時間分別為原模型的4.05%、12.4%。

（2）以某型航空發動機某級帶內環的整流為例，建立了8、6、4和2簡化模型，前5階模態振型與原模型吻合較好，固有頻率最大誤差分別為2.72%、4.23%、4.73%和7.32%；模型總自由度數分別減至原模型的2.55%、2.46%、2.35%和2.31%；在相同條件下，計算時間縮至1.89%、1.72%、1.65%和1.42%。

（3）仿真計算結果表明，截面等效葉片建模簡化方法不僅大大簡化了有限元模型規模，而且達到了一定的計算精度，具有一定的工程應用價值。

[1]Sinou J J，Villa C，Thouverez F，et al.Experimental and numerical investigations of a flexible rotor on flexible bearing supports[J].International Journal of Rotating Machinery，2005（3）：179-189.

[2]Hanhart A L，Gobbert A M，Izu L T.A memory-efficient finite element method for systems of reaction diffusion equations with non-smooth forcing [J].Journal of Computational and Applied Mathematics，2004，169（2）：431-458.

[3]Morre J J，Vannini G，Camatti M，et al.Rotor dynamic analysis of a large industrial turbo-compressor including finite element substructure modeling[J].Journal of Engineering for Gas Turbines and Power，2010，132（8）：1-9.

[4]Hong J，Chen M，Liu S G.Application of whole engine finite element models in aeroengine rotor dynamic simulation analysis[C]//Proceedings of ASME Turbo Expo 2007.Power for Land，Sea and Air，Montreal：ASME，2007:771-778.

[5]Sch?nrock A，Dascotte E，Dufour K H.Validation of an aeroengine carcass finite element model by means of computational model updating based on static stiffness testing[C]//2nd MSC Aerospace Conference，Long Beach:CA,1999：1-8.

[6]王海濤.某型航空發動機整機振動特性分析[D].南京：南京航空航天大學，2010.WANG Haitao.Research on whole body vibration of aeroengine[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2010.(in Chinese)

[7]洪杰，郝勇，張博，等.葉片丟失激勵下整機力學行為及其動力特性[J].航空發動機，2014，40（2）：19-23.HONG Jie，HAO Yong，ZHANG Bo，et al.Mechanical behaviors and dynamic characteristics of turbofan engine due to fan blade off[J].Aeroengine，2014，40（2）：19-23.(in Chinese)

[8]趙文濤，陳果，李瓊，等.航空發動機機匣支承動剛度有限元計算及驗證[J].航空計算技術，2011（5）：34-38，41.ZHAO Wentao，CHEN Guo，LI Qiong，et al.Finite element modeling and experiment verification of dynamic stiffness of casing bearing in aircraft engine[J].Aeronautical Computing Technique，2011，41（5）：34-38，41.(in Chinese)

[9]王相平，徐鶴山.有限元計算中的葉片邊界條件的選取[J].航空發動機，1998（4）：43-46，57.WANG Xiangping，XU Heshan.Finite element method of blade boundary conditions[J].Aeroengine，1998，9（4）：43-46，57.(in Chinese)

[10]白中祥，吳偉亮，劉閎釗.支承系統的剛度對轉子動力特性的影響[J].機械設計與研究，2012，28（4）：19-21，25.BAI Zhongxiang，WU Weiliang，LIU Hongzhao.The effect of the stiffness of a rotor’s supporting system on its dynamic characteristics[J].Machine Design and Research，2012，28（4）：19-21，25.(in Chinese)

[11]高金海，洪杰.航空發動機整機動力特性建模技術研究[J].戰術導彈技術，2006（3）：29-35.GAO Jinhai，HONG Jie.Study of modeling technique for dynamic characteristics of engine casing[J].Tactical Missile Technology，2006（3）：29-35.(in Chinese)

[12]張力，洪杰，馬艷紅.航空發動機轉子系統建模方法和振動特性分析[J].北京航空航天大學學報，2013（2）：148-153，163.ZHANG Li，HONG Jie，MA Yanhong.Modeling method and vibration characteristics of aero-engine rotor system [J].Journal of Beijing University of Aeronautics and Astronautics，2013（2）：148-153，163.(in Chinese)

[13]邵帥，周柏卓，王相平.失諧葉盤結構振動模態局部化研究[J].航空發動機，2014，40（3）：56-59.SHAO Shuai，ZHOU Baizhuo，WANG Xiangping.Investigation of vibration mode localization of mistuned bladed-disk assemblies[J].Aeroengine，2014，40（3）：56-59.(in Chinese)

[14]馬輝，能海強，宋溶澤，等.基于變厚度殼單元的旋轉葉片固有特性分析[J].航空發動機，2013，39（5）：26-30.MA Hui，NAI Haiqiang，SONG Rongze，et al.Natural characteristic analysis of rotating blade based on variable thickness shell element[J].Aeroengine，2013，39（5）：26-30.(in Chinese)

[15]漆文凱，王向輝.基于轉靜子耦合的組合壓氣機動力特性分析[J].航空發動機，2014，40（4）：46-50.QI Wenkai，WANG Xianghui.Analysis on dynamic characteristics of combined compressor based on coupling of rotor and stator[J].Aeroengine，2014，40（4）：46-50.(in Chinese)