一種基于CKF的無線傳感器網(wǎng)絡(luò)分布式定位算法

余木琪，鄧 平

（西南交通大學(xué)信息編碼與傳輸重點實驗室，成都 610031）

一種基于CKF的無線傳感器網(wǎng)絡(luò)分布式定位算法

余木琪，鄧 平*

（西南交通大學(xué)信息編碼與傳輸重點實驗室，成都 610031）

為提高無線傳感器網(wǎng)絡(luò)節(jié)點定位的精度，降低算法計算復(fù)雜性，提出了一種基于容積卡爾曼濾波的無線傳感器網(wǎng)絡(luò)分布式節(jié)點定位算法。該算法假定移動錨節(jié)點按預(yù)定路徑在傳感區(qū)域移動，并周期性廣播自身位置信標(biāo)信息；每個未知位置節(jié)點首先收集多個錨節(jié)點信標(biāo)信息及信號強度信息，然后估算出錨節(jié)點信標(biāo)位置與未知節(jié)點的距離，最后在未知節(jié)點上運用容積卡爾曼濾波算法完成自身位置的分布式定位。仿真結(jié)果表明：本文所提算法具有優(yōu)良的定位性能，定位精度和無跡卡爾曼濾波算法相當(dāng)，明顯優(yōu)于極大似然估計定位算法，而計算復(fù)雜性則低于無跡卡爾曼濾波算法。

無線傳感器網(wǎng)絡(luò)；容積卡爾曼濾波；定位；移動錨節(jié)點

無線傳感器網(wǎng)絡(luò)（Wireless Sensor Networks，WSN）是由布置在監(jiān)測區(qū)域內(nèi)大量的廉價微型傳感器節(jié)點組成，通過無線通信方式形成的一個多跳自組織網(wǎng)絡(luò)，其目的是協(xié)作地感知、采集和處理網(wǎng)絡(luò)覆蓋區(qū)域中監(jiān)測對象的信息，并發(fā)送給觀察者［1］。無線傳感器網(wǎng)絡(luò)涉及傳感器技術(shù)、微機電系統(tǒng)、現(xiàn)代網(wǎng)絡(luò)和無線通信等技術(shù)，是21世紀(jì)最重要的新興技術(shù)之一，也是目前IT領(lǐng)域中的研究熱點之一［2］。在無線傳感器網(wǎng)絡(luò)中，節(jié)點的位置信息對網(wǎng)絡(luò)的監(jiān)測活動至關(guān)重要。

近年來，無線傳感器網(wǎng)絡(luò)節(jié)點定位技術(shù)得到飛速發(fā)展，主要的定位算法有測距定位、非測距定位、凸優(yōu)化、移動錨節(jié)點定位、蒙特卡洛定位（Monte Caro localization，MCL）等算法［3-5］。文獻(xiàn)［5］中Lingxuan Hu和David Evans參考移動機器人中的序列蒙特卡洛定位方法的思想，首次將MCL應(yīng)用于移動傳感網(wǎng)的定位中，但是該算法需要很高的錨節(jié)點密度才能獲得比較好的定位精度，計算復(fù)雜度高，且不能應(yīng)用于節(jié)點靜止的無線傳感器網(wǎng)絡(luò)的節(jié)點定位。文獻(xiàn)［6］中Liqiang Zhang等人將目標(biāo)跟蹤的過程運用于移動錨節(jié)點的無線傳感器網(wǎng)絡(luò)分布式定位，提出一種新的分布式傳感器定位算法。該算法運用無跡卡爾曼濾波（Unscented Kalman Filter，UKF）進行定位，能取得較高的定位精度，但是UKF算法的可調(diào)參數(shù)選取不好會使其不穩(wěn)定。文獻(xiàn)［7］對文獻(xiàn)［6］的初始位置選取進行改進，首先接收三個不共線的錨節(jié)點信標(biāo)信息，運用三邊測量法定位出未知節(jié)點的粗略初始位置，再運用UKF算法完成定位。該算法在錨節(jié)點發(fā)送信標(biāo)信息密集時出現(xiàn)局部線性，使得該算法長時間選取不到不共線的信標(biāo)，無法及時得到初始位置，進而使得運行時間過長。

容積卡爾曼濾波（Cubature Kalman Filter，CKF）是Ienkaran Arasaratnam和Simon Haykin于2009年提出的一種濾波估計精度高、穩(wěn)定性好、計算量小的非線性濾波方法［8-9］。近年來有許多研究者對CKF算法進行改進，并應(yīng)用于列車導(dǎo)航定位、目標(biāo)跟蹤等領(lǐng)域，但目前還未見到研究者將其應(yīng)用于無線傳感器網(wǎng)絡(luò)節(jié)點定位中。

本文借鑒Liqiang Zhang等人所提算法的思想，將容積卡爾曼濾波運用于無線傳感器網(wǎng)絡(luò)節(jié)點定位中，提出一種基于容積卡爾曼濾波的無線傳感器網(wǎng)絡(luò)節(jié)點分布式定位算法。該算法的主要步驟為：移動錨節(jié)點按預(yù)定路徑在傳感區(qū)域移動，并周期性廣播自身位置信息；每個未知位置節(jié)點首先收集錨節(jié)點位置信息及對應(yīng)的信號強度信息，然后估算出錨節(jié)點與未知節(jié)點的距離，最后在未知節(jié)點上運用CKF算法完成自身位置的定位。

本文首先給出移動錨節(jié)點定位模型，然后分析了容積卡爾曼濾波算法的特點，給出了詳細(xì)的算法步驟，接著詳細(xì)介紹了基于CKF的WSN節(jié)點分布式定位的算法流程，最后建立仿真環(huán)境，仿真分析了測距誤差、錨節(jié)點信標(biāo)個數(shù)、初始位置對本文算法定位精度的影響，并與文獻(xiàn)［6］所提UKF算法及極大似然估計定位法的性能進行了仿真比較。

1 移動錨節(jié)點定位模型

假設(shè)無線傳感器網(wǎng)絡(luò)中有N個傳感器節(jié)點，第i （i=1,…,N）個傳感器節(jié)點在k時刻的系統(tǒng)狀態(tài)為Xi（k）=［Xi1（k）,Xi2（k）,Xi3（k）］T。本文考慮靜止的傳感器節(jié)點，則移動錨節(jié)點定位系統(tǒng)的狀態(tài)方程和觀測方程如下：

取傳感器節(jié)點i在k時刻與移動錨節(jié)點之間的距離作為觀測量，

2 容積卡爾曼濾波算法

卡爾曼濾波是最經(jīng)典的濾波估計方法，但只適用于線性觀測方程，擴展卡爾曼濾波（Extended Kalman Filter，EKF）是傳統(tǒng)處理非線性方程的濾波估計方法，EKF能夠達(dá)到一階泰勒展式的精度，但在非線性度偏高的場合會出現(xiàn)濾波發(fā)散［10］。無跡卡爾曼濾波是一種求sigma點的非線性濾波方法，該算法精度高，能夠達(dá)到二階甚至三階泰勒展式的精度，但是該算法的主要弱點是不穩(wěn)定［11］。

容積卡爾曼濾波算法的基本思想仍然是一種“預(yù)測—校正”的經(jīng)典卡爾曼濾波結(jié)構(gòu)下的估計算法，它與EKF、UKF相同，同屬于高斯域貝葉斯濾波的結(jié)構(gòu)范疇，但是CKF因其實現(xiàn)簡單、非線性逼近特性強等優(yōu)點，在與傳統(tǒng)非線性算法策略的比較中具有極大的優(yōu)勢。CKF采用了UKF類似的點集近似分布方法，能夠獲得比EKF更高的非線性逼近性能［12］，當(dāng)UKF的參數(shù)κ=0時，CKF 與UKF的濾波性能一致［13-14］。相比于UKF，CKF具備的主要優(yōu)勢有［12］：對三維以上的狀態(tài)方程，濾波精度更高，可采用平方根策略求解，濾波穩(wěn)定性更優(yōu)。

容積卡爾曼濾波算法的基本步驟如下。

2.1 時間更新

①假設(shè)在k-1時刻的估計方差已知，對其分解得

②計算Cubature點

③計算更新后的Cubature點

④計算一步預(yù)測狀態(tài)

⑤計算一步預(yù)測誤差方差

2.2 測量更新

①對一步預(yù)測誤差方差進行分解

②計算cubature點

③計算通過量測方程的Cubature點

④計算量測估計值

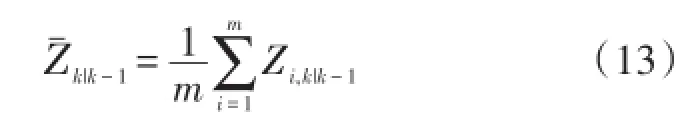
⑤計算更新后的量測誤差方差

⑥計算協(xié)方差

⑦計算卡爾曼濾波增益

⑧ 計算更新后的狀態(tài)

⑨ 計算相應(yīng)的估計誤差方差

3 基于CKF的WSN節(jié)點定位算法

在無線傳感器網(wǎng)絡(luò)中，移動錨節(jié)點按規(guī)定的移動路徑在傳感區(qū)域移動，周期性廣播自身位置信息，每個未知節(jié)點收集錨節(jié)點位置信息并計算出錨節(jié)點與未知節(jié)點的距離，對每個未知節(jié)點獨立運用容積卡爾曼濾波定位出自身位置坐標(biāo)。該算法的流程圖如圖1所示。

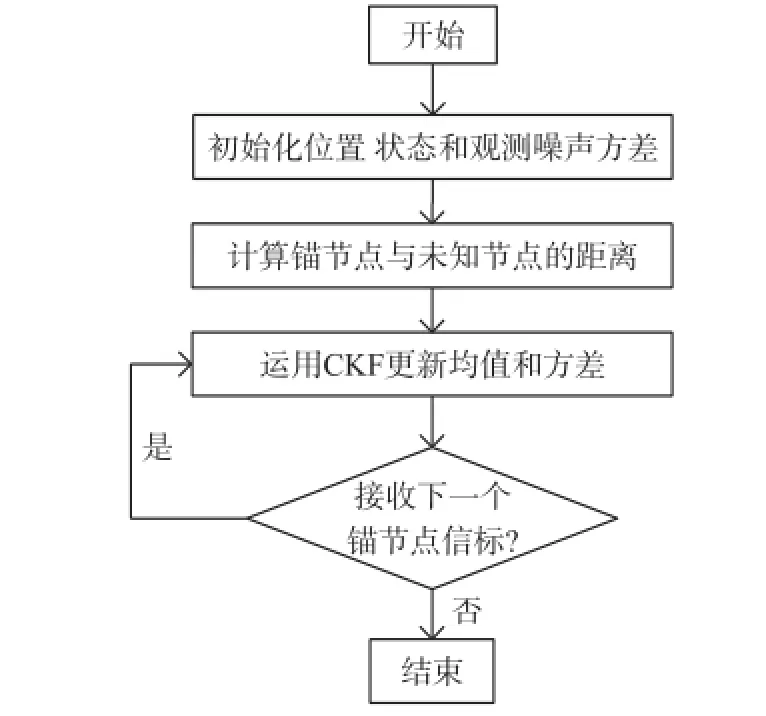
圖1 基于CKF的WSN節(jié)點定位算法流程圖

4 定位性能仿真分析

［6］的仿真場景，本文假設(shè)在1 000 m×1 000 m的傳感區(qū)域內(nèi)隨機布置N=200個傳感器節(jié)點。假設(shè)所有未知位置節(jié)點進行迭代估計的初始位置設(shè)置為傳感區(qū)域的中心，即x（0）=（500,500），假設(shè)狀態(tài)過程噪聲方差矩陣為Q=diag（［0.001,0.001,0.001］），測 距 誤 差 為range_error=10%，觀測噪聲方差為 R=（700*2* range_error）2*sc，其中sc表示觀測噪聲方差放大因子，假設(shè) sc=0.01，初始位置噪聲方差矩陣為P=100*diag（［1,1,1］），取迭代次數(shù)，即移動錨節(jié)點廣播信標(biāo)的個數(shù)為100，以下仿真中若未做特殊說明，初始條件不變。移動錨節(jié)點在距離傳感區(qū)域100 m高的平面按圓心為（500 m，500 m）、半徑為700 m的圓形路徑移動，該圓形覆蓋了整個傳感區(qū)域。錨節(jié)點每圈廣播信標(biāo)個數(shù)為beacons_per_round=15，在該仿真場景中，移動錨節(jié)點在k時刻的坐標(biāo)表示為

假設(shè)距離測量值的誤差主要由高斯噪聲引起，則測量距離與真實距離之間的關(guān)系表示如下：

其中dˉ為測量距離，d為真實距離，range_error為［0,1］之間的一個固定值，randn（1）是標(biāo)準(zhǔn)的正態(tài)隨機變量。

本文選取平均定位誤差（Mean Positioning Error，MPE）作為定位精度評價標(biāo)準(zhǔn)，定義：位置節(jié)點的真實位置

算法的計算復(fù)雜性，即時間復(fù)雜度，是指執(zhí)行算法所需要的計算工作量，它定量描述了該算法的運行時間，決定了算法的運行時間長短，即計算復(fù)雜性越低，運行時間越短，算法性能越優(yōu)。本文選取算法的運行時間作為計算復(fù)雜性的評價標(biāo)準(zhǔn)。

4.1 測距誤差對定位精度的影響

測距的精確度對無線傳感器網(wǎng)絡(luò)節(jié)點定位有很大的影響，通常測距精度越高，定位的精度也越高，反之，測距精度越低，定位的精度也越低。本次仿真選取4種不同的測距誤差，range_error分別為5%、10%、15%、20%。仿真得出測距誤差對定位精度的影響如圖2所示。

圖2 測距誤差對定位精度的影響

由圖2可以看出錨節(jié)點信標(biāo)個數(shù)相同的情況下，隨著測距誤差的增加，定位精度降低。

4.2 錨節(jié)點信標(biāo)個數(shù)對定位精度的影響

由圖2可以看出，隨著錨節(jié)點信標(biāo)個數(shù)的增加，定位精度增高。然而，錨節(jié)點過多不僅會增加通信負(fù)荷，而且會加大每個傳感器節(jié)點的運算量。本節(jié)研究錨節(jié)點信標(biāo)總數(shù)相同的情況下，錨節(jié)點每圈廣播信標(biāo)個數(shù)對定位精度的影響。設(shè)置錨節(jié)點每圈廣播信標(biāo)個數(shù)分別為15、60、240時，錨節(jié)點信標(biāo)個數(shù)與定位精度的關(guān)系如圖3。

圖3 錨節(jié)點每圈廣播信標(biāo)個數(shù)對定位精度的影響

由圖3可以看出錨節(jié)點總數(shù)固定的情況下，錨節(jié)點每圈廣播個數(shù)越少，定位精度越高，這主要是幾何精度因子對定位所產(chǎn)生的影響。

4.3 初始位置對定位精度的影響

初始參數(shù)對卡爾曼濾波的性能有著不可忽視的影響，不同的初始位置、位置方差、觀測噪聲方差、狀態(tài)噪聲方差都會對定位產(chǎn)生很大的影響。本次仿真取三邊測量法估計的初始位置、傳感區(qū)域的圓心（500，500）、圓外（1210，500）。圖4為不同的初始位置對定位精度的影響。

由圖4可以看出先運用三邊測量法估計出未知位置節(jié)點的粗略初始位置，再進行CKF迭代，其定位精度明顯高于于初始位置在圓心和圓外。

圖4 初始位置對定位精度的影響

4.4CKF、UKF、MLE定位算法比較

圖5仿真了CKF、UKF、MLE三種定位算法的定位精度比較。由圖5可以看出，CKF和UKF運用于無線傳感器網(wǎng)絡(luò)節(jié)點定位，具有相同的定位精度，且高于MLE。圖6為對基于CKF的WSN節(jié)點定位算法和基于UKF的WSN節(jié)點定位算法分別進行50次蒙特卡洛仿真，得出的運行時間比較圖，本次仿真采樣的錨節(jié)點信標(biāo)總數(shù)為50個，仿真環(huán)境為Windows XP系統(tǒng)下的MATLAB R2010（a）。由圖6可以看出，CKF算法的運行時間低于UKF算法，即CKF算法的計算復(fù)雜性低于UKF算法。

圖5 UKF、CKF、MLE的定位精度比較

圖6 CKF、UKF運行時間比較

5 結(jié)論

本文研究無線傳感器網(wǎng)絡(luò)節(jié)點定位問題，提出一種基于容積卡爾曼濾波的無線傳感器網(wǎng)絡(luò)分布式定位算法。該算法無需節(jié)點間通信，具有較高的定位精度和較低的計算復(fù)雜性。仿真驗證了本文算法的定位精度與UKF算法相同，明顯優(yōu)于極大似然估計定位算法，而計算復(fù)雜性則低于UKF算法。

參考文獻(xiàn)：

［1］ Akyildiz I F，Su W，Sankarasubramaniam Y，et al.Wireless Sensor Networks：A Survey［J］.Computer Networks，2002，38（4）：393-422.

［2］ Chong C Y，Kumar S P.Sensor Networks：Evolution，Opportunities，and Challenges［C］//Proceedings of the IEEE，2003：1247-1256.

［3］ 何國剛，鄧平.一種高斯噪聲下基于最大分散度的WSN半定規(guī)劃定位算法［J］.傳感技術(shù)學(xué)報，2012，25（8）：1004-1699.

［4］ 王靜，鄧平.一種基于邊松弛的大規(guī)模WSN分簇定位算法［J］.傳感技術(shù)學(xué)報，2013，26（5）：683-688.

［5］ Lingxuan Hu，David Evans.Localization for Mobile Sensor Networks［J］.MobiCom'04，2004：45-57.

［6］ Zhang Liqiang，Cheng Qiang，Wang Yingge，et al.A Novel Distributed Sensor Positioning System Using the Dual of Target Tracking ［J］.IEEE Transactions on Computers，2008，57（2）：246-260.

［7］ Hu Weiwei，Qin Huibin，Huang Haiyun.A Mobile Beacon Based Method for Wireless Sensor Networks Localization［C］//IEEE International Conference on Communication Technology Proceedings，2008：144-147.

［8］ Ienkaran Arasaratnam，Simon Haykin.Cubature Kalman Filters ［J］.IEEE Transaction on Automatic Control，2009，54（6）：1254-1269.

［9］ Ienkaran Arasaratnam，Simon Haykin，Thomas R Hurd.Cubature Kalman Filtering for Continuous-Discrete Systems：Theory and Simulations［J］.IEEE Transactions on Signal Processing，2010，58 （10）：4977-4993.

［10］Fred Daum.Nonlinear Filters：Beyond the Kalman Filter［J］. IEEE A&E Systems Magazine，2005，20（8）：57-69.

［11］Simon J Julier，Jeffrey K Uhlmann.Unscented Filtering and Nonlinear Estimation［C］//Proceedings of the IEEE，2004，92（3）：401-422.

［12］蔡伯根.低成本列控系統(tǒng)的列車組合定位理論與方法［D］.北京：北京交通大學(xué)，2010：54-58.

［13］Chang Lubin，Hu Baiqing，Li An，et al.Transformed Unscented Kalman Filter［J］.IEEE Transactions on Automatic Control，2013，58（1）：252-257.

［14］孫楓，唐李軍.Cubature卡爾曼濾波與Unscented卡爾曼濾波估計精度比較［J］.控制與決策，2013，28（2）：303-308.

余木琪（1989-），男，漢族，碩士研究生。主要從事無線傳感器網(wǎng)絡(luò)定位跟蹤技術(shù)的研究；

鄧 平（1964-），男，漢族，博士，教授。主要研究方向有無線網(wǎng)絡(luò)定位技術(shù)，現(xiàn)代信號處理，無線傳感器網(wǎng)絡(luò)等。

A Distributed Localization Algorithm Based on Cubature Kalman Filter in Wireless Sensor Networks

YU Muqi，DENG Ping*
（Key lab of information coding and transmission，Southwest JIAOTONG University，Chengdu 610031，China）

To improve the localization accuracy and decrease the computation complexity，a distributed node localization algorithm based on cubature kalman filter in wireless sensor networks is proposed.The algorithm supposes that a mobile beacon moves by predetermined trajectory around a sensor field，and periodically broadcasts its current location.Each sensor collects the location and RSS of beacons，measures the distance between itself and the beacon，and individually calculates their locations via a Cubature Kalman Filter algorithm.Simulations show that the proposed algorithm has a good localization performance，the localization accuracy is same to the UKF algorithm，better than the MLE localization algorithm，and the computation complexity is smaller than the UKF algorithm.

WSN；CKF；localization；moving beacon EEACC：7230

TP393

A

1004-1699（2015）07-1041-05

10.3969/j.issn.1004-1699.2015.07.017

2015-01-30 修改日期：2015-03-09