一類二次半定規劃Gauss-Newton方向的存在唯一性

游 揚，張圣貴

（1．福州外語外貿學院，福建 福州 350202；2.福建師范大學 數學與計算機科學學院）

一類二次半定規劃Gauss-Newton方向的存在唯一性

游 揚1，張圣貴2

（1．福州外語外貿學院，福建 福州 350202；2.福建師范大學 數學與計算機科學學院）

本文在半定規劃中的Gauss-Newton搜索方向的基礎上研究一類特殊的二次半定規劃（QSDP）求解問題，基于矩陣論和和凸規劃理論中原始-對偶算法的NT搜索方向將此類二次半定規劃問題轉化為求解線性半定規劃的最小二乘問題，為了驗證此理論的可行性本文驗證了Gauss-Newton搜索方向在最小二乘問題中的存在性和唯一性.

半定規劃；二次半定規劃（QSDP）；最小二乘問題；線性最小二乘問題（LQ）；Gauss-Newton方向

1 引言

近年來，半定規劃（SDP）是最優化理論領域發展較完善、應用最廣泛的規劃.伴隨著半定規劃的發展，原始對偶內點算法已成為解決此類問題最有效的算法中的一員.20世紀90年代末隨著線性半定規劃的日趨成熟，人們自然而然地開始考慮更為復雜的半定規劃——非線性半定規劃，其中最為簡單的一種規劃就是二次半定規劃（QSDP）.它在系統論、控制論等諸多領域具有著廣泛的應用，而且憑借著矩陣理論和原始對偶算法中NT方向的相關理論可以將二次半定規劃轉化為線性半定最小二乘問題，使得二次半定規劃在證券，金融風險分析，穩健性二次優化等領域中起著非常重要的作用.

在半定規劃的原始對偶內點算法中目前為止已經被驗證的應用最為廣泛的搜索方向主要有如下四種：①AHO方向［1］；②K..S..H方向［2］；③H..K..M方向［3］；④NT方向［4］.其中NT方向和H..K..M方向已被人成功地推廣到某類二次半定規劃上［6，12］.到目前為止NT方向被認為是此四個方向中應用最廣泛最有效的的搜索方向.在找尋搜索方向時采用牛頓法，借助對稱化將互補松弛條件用來求解KKT系統，搜索方向的合理性雖然得到了保障，但求解的過程不僅增加計算的復雜性而且容易導致KKT系統的不穩定.故而此方法還尚待完善.在文獻［5］中SergeKruk等學者提出了用于求解線性SDP的新搜索方向即Gauss-Newton方向.若改用此方向可以避免松弛條件的對稱化過程，計算的復雜性就得以降低，系統的穩定性也相應的增強.基于此，，本文選取具有特殊算子的一類QSDP，以NT方向為基礎將其推廣成二次半定規劃中的Gauss-Newton方向，并運用優化中的相關理論證明了Gauss-Newton方向的存在唯一性.

2 QSDP的Gauss-Newton搜索方向的存在唯一性

二次半定規劃的一般形式為

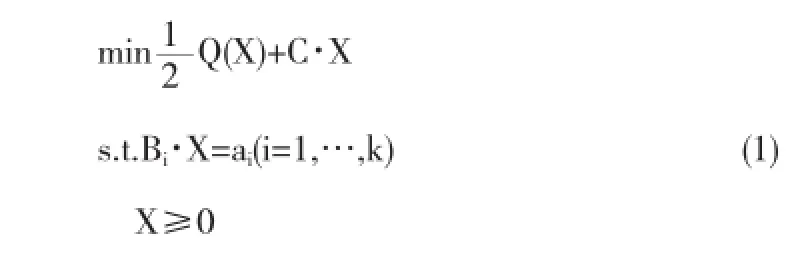
其中Q是Sn到Sn的具有半正定性質的自伴隨線性算子，X≥0規定X為半正定矩陣，Bi是n階實對稱陣（i=1，…，k），且B1，…，Bk是線性無關的，ai為n維列向量.

再由KKT條件以及類似于文獻［6］的處理方法利用松弛條件對上述半定規劃（2）進行改寫，得到了擾動方程組

上述系統（3）的解被稱為中心路徑，記為（X（μ），λ（μ），Z（μ），其中μ為中心路徑參數.

若規定原始對偶算法中變量X，Z迭代過程產生的下一步步長分別為ΔX，ΔZ，故此步長變量在理想情形下即為如下系統的解［7］

正是因為系統（4）的非線性，zhang等學者在文獻［8］中利用互補松弛條件的對稱化這一技巧將此系統轉化為線性系統.但這一過程卻大大增加了系統計算的復雜性，在1998年Kruk于文獻［5］中將此非線性系統問題轉化為最小二乘問題來考慮，并在文中嚴謹地證明了求解此類問題的Gauss-Newton方向的存在性和唯一性.基于上述事實，本文將此方法加以推廣用以求解下列最小二乘問題（5），并推導出求解系統（3）相應的Gauss-Newton方向，最后論證該搜索方向的存在性和唯一性.

系統（4）可等價地改寫為如下最小二乘問題：

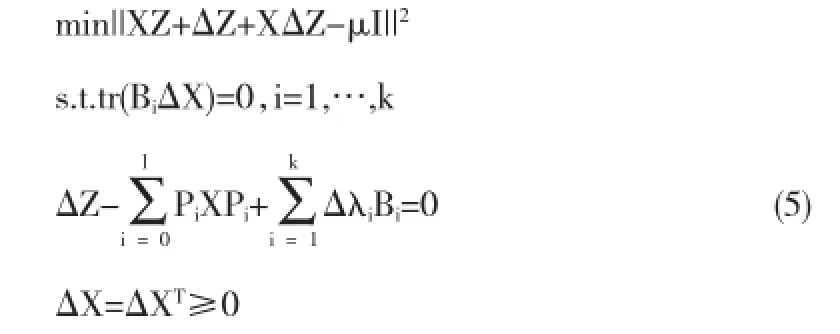
由文獻［6］中的NT方向，定義如下矩陣

從而系統（6）可等價轉化為

由于問題（7）中含有非線性項WX，WZ，直接求解此最小二乘問題很繁瑣.文獻［5］已經證明忽略問題中出現的非線性項WX，WZ不會改變該問題本身固有屬性，并忽略此項后，因為所取范數的類型決定了該最小二乘問題的最優解，故當所給問題的范數類型確定時問題也隨之被唯一確定.這里選取由內積導出的范數.內積做如下定義：：此內積可被看作是由障礙函數f（V）=-lndet（V）的Hessian矩陣誘導出的局部范數.因為f的Hessian矩陣V的值是一個線性的算子▽2f（V）：H→V-1HV-1.所以我們就相應的得到如下最小二乘問題［7］

這里最小二乘問題的范數取F-范數［9］.為了方便敘述，

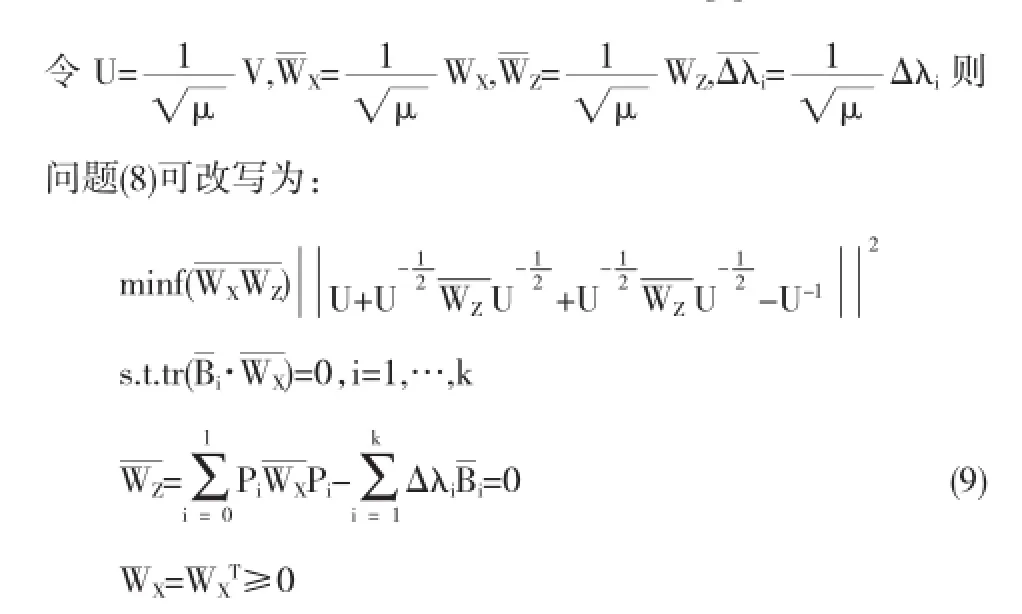
如果問題（10）只存在零解，我們便可以推出問題（9）有唯一解.因此下面主要驗證問題（10）只存在零解.因為問題（10）

3 問題與總結

本文以線性半定規劃的Gauss-Newton方向以及二次半定規劃 （QSDP）的NT搜索方向的理論為基礎，將Gauss-Newton方向從LSDP推廣到一類特殊的QSDP，并驗證了Gauss-Newton方向的存在性及其唯一性.但本文中只給出了與原始問題等價的線性最小二乘問題，在文獻［11］中研究者A.Bjorck提出了用矩陣QR分解簡化求解此類問題，若可以將其推廣并應用到本文所提的優化問題中，便將進一步完善本文所提理論的系統性.

〔1〕F.Alizadeh，J.P.A.Haeberly and M.L.Overton.Primal dual methods for semidefinite programming：convergence rates，stability and numerical results［J］.SIAM J.Optim.，1998，8（3）：746-768.

〔2〕R.D.C.Monteiro.Primal dual path following algorithms for semidefinite programming［J］.SIAM J.Optim.，1997，7：663-678.

〔3〕M.Kojima，S.Shindoh and S.Hara.Interiorpoint methods for the monotone semidefinite complementarity promble in symmtric matrices［J］.SIAM J.Optim.，1997，7：86-125.

〔4〕M.J.Todd， K.C.Toh and R.H.Tutuncu. On the Nesterov-Todd direction in semidefinite programming［J］. SIAM J.Optim.，1998，8（3）：769-796.

〔5〕S.Kruk，M.Muramatsu，F.Rendletal.TheGauss-Newton direction in semidefinite programming［J］. Optimization Methods and Software，2001，issue 1：1-28.

〔6〕游揚，張圣貴.一類二次半定規劃內點算法的K..S..H搜索方向的存在唯一性［J］.福建師范大學學報（自然科學版），2012，28（1）：16-20.

〔7〕E.deKlerk，J.Peng，C.Roos， T.Terlaky.A scaled Gauss-Newton Primal-DualSearch Direction for Semidefinite Optimization.http：//citeseerx.ist.psu. edu/ viewdoc.

〔8〕Y.Zhang.On extending some primal-dualinterior point algorithms from linear programming to semidefinite programming.SIAM Journal on Optimization，1998，8（2）：365-386.

〔9〕陳寶林.最優化理論與算法（第2版）［M］.北京：清華大學出版社，2005.10.

〔10〕Dimitri P.Bertsekas with Angelia Nedic and Asuman E. Ozdaglar.Convex Analysis and Optimization：凸分析與優化（第二版）［M］.北京：清華大學出版社，2006.2.

〔11〕A.Bjorck.NumericalMethods for Least Squares Problems.SIAM，Philadelphia，1996.

〔12〕黃靜靜，王愛文.二次半定規劃的原始對偶內點算法的H..K..M搜索方向的存在唯一性 ［J］.數學實踐與認識，2008，38（18）：233-238.

O221

A

1673-260X（2015）05-0001-03

福建省教育廳B類項目（JB13364S）資助