積分變限函數求導研究
2015-11-15 07:59:42常安成湖南信息學院
消費導刊 2015年11期
常安成 湖南信息學院
積分變限函數求導研究
常安成 湖南信息學院
本文先回顧積分上限函數的求導問題,然后由易至難逐步研究一些較為復雜的變限函數的求導問題,最后得到一個重要的定理。
變限函數 函數求導 分離變量函數
為了介紹牛頓——萊布尼茲公式,我們引入了積分上限公式函數。這是一個很重要的函數,有著很好的性質,只要在上連續,就一定有可導,且有求導公式。可以看出函數是函數的一個原函數,這就解決了不定積分中沒能證明的結論:連續函數必有原函數。容易推出。下面我們對更一般的積分上限函數(或稱變限函數)的求導作進一步的研究。
一、變限函數的導數
所以由復合函數求導法則可得
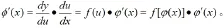
二、變限函數的導數
那么它的導數可用乘積的求導法則解決:
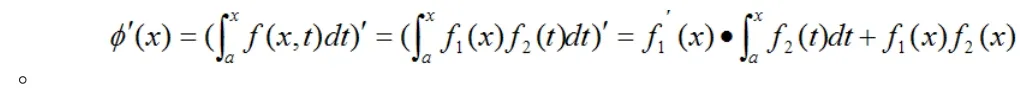
這是一個相當抽象的函數,我們知道對于抽象函數的求導一般使用定義來求函數增量:
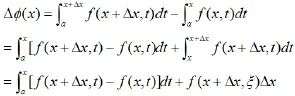
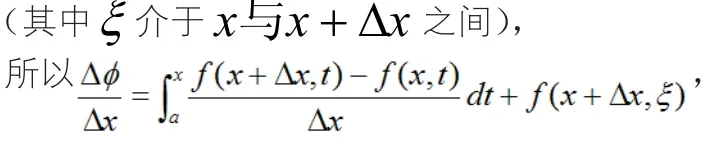
三、研究結論
從上面的情況分析,我們可以得出本文研究所得的結論:
我們現在應用這個定理來解答一道題,并也用分離變量的方法解答此題,以此來對比這兩個方法解題的效果如何。
方法一:應用定理解答
有定理得:
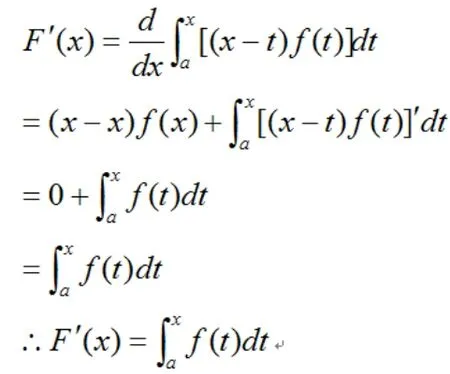
方法二:應用分離變量的方法解答
解:因為
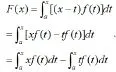
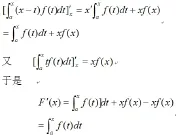
從以上解題效果看,用定理解題要比用分離變量的方法解題簡單方便快捷。況且,定理既可以應用于可分離變量的情況,又可應用于不可分離變量的情況。此定理對于解決復雜的積分變上限函數的求導給予了一種便捷的解法,以供參考。
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
兒童故事畫報(2019年5期)2019-05-26 14:26:14
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12

