多杯等流型氣錨應用試驗效果統計誤差評價

孫 哲，孫 巍

（東北石油大學 提高油氣采收率教育部重點實驗室，黑龍江 大慶 163318）

在采油過程中，油井都會采出或多或少的伴生天然氣[1,2]。井下氣錨可以使進泵流體在進泵前實現氣液分離，降低氣體對抽油泵的影響，從而提高抽油泵泵效和油井產量。

在油田生產中使用的常規氣錨有偏心氣錨[3]、螺旋式氣錨[4]、賈敏氣錨[5]、旋流式氣錨[6]、和迷宮式氣錨等，這些氣錨的氣液分離區域短，在分離過程中氣體容易充滿氣錨，分離效果不理想。多杯等流型氣錨是建立在油氣密度差的基礎上，通過延長油井產出液在沉降杯中的滯留時間提高該氣錨的脫氣效率[7]。

因此，多杯等流型氣錨得到了越來越廣泛的應用，而其應用效果的評價不僅工作量大，而且關系到多杯等流型氣錨在油田的推廣前景，因此開展多杯等流型氣錨應用試驗效果統計誤差評價具有理論和工程意義。

1 理論基礎

1.1 定義

定義1：置信區間：設總體X有待估參數q，X1,X2,…,Xn是抽自該總體的一個容量為n的簡單隨機樣本。現建立兩個統計量和，且￡，a是一給定的概率，稱為顯著性水平，1-a稱為置信水平。若成立，則稱隨機區間為參數q在置信水平1-a下的置信區間。

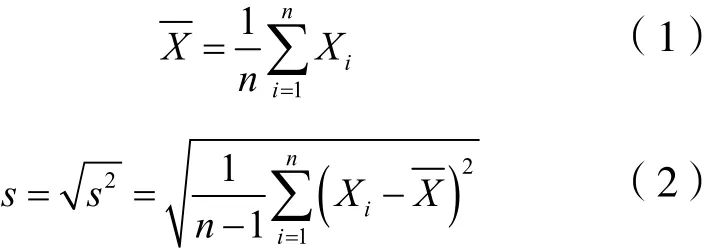
式中：n— 樣本容量，無因次。

1.2 抽樣誤差與置信區間

當總體方差 s2為未知時，設X1,X2,…,Xn為服從總體 N(m, s2)的一個樣本，由于 s2未知，我們常用樣本方差 s2估計總體方差 s2，此時統計量，對于給定的顯著性水平a，根據t分布表可以確定 m的雙側臨界值 ta/2(n - 1) ，使得成立。

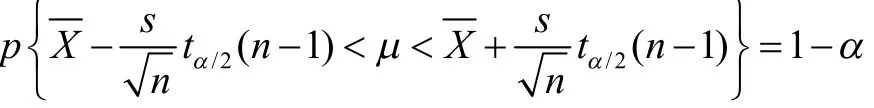
可得總體均值m的置信水平為1-a的置信區間為[9]：

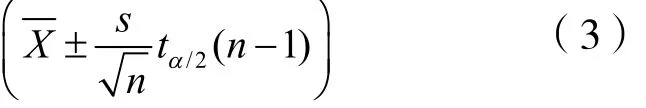
則

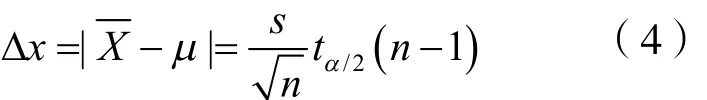
式中：Dx— 抽樣誤差，無因次。

1.3 誤差傳遞

設 x*為準確數x的一個近似數，則兩者之差或差的絕對值，即

為近似數 x*的絕對誤差，即為計算出的抽樣誤差Dx。

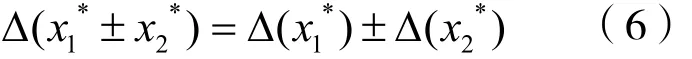
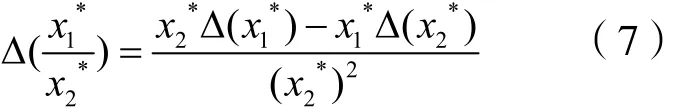
2 計算方法

1）科學合理的確定抽樣測量的井數n，保證推算的精確度和抽樣推斷的最大效果；

2）合理的確定置信水平1-a，對估計的精確度和可靠性的要求應根據現場實際情況來考慮。根據現場實際情況，設定置信水平1-a為90.0%；

3）計算樣本的抽樣指標，根據公式（1）計算下氣錨后各月產液量、產油量和沉沒度數據的樣本平均值。根據公式（2）計算下氣錨后各月產液量、產油量和沉沒度數據的樣本標準差，計算出的樣本平均值和樣本標準差，作為總體指標的估計值；

4）根據給定的置信水平1-a和抽樣測量的井數n，利用統計函數 TINV或者查閱t分布表求出ta/2(n - 1)的值；

5）由公式（4）來計算下氣錨后各月產液量、產油量和沉沒度數據樣本均值的抽樣誤差Dx，并由公式（3）求出被估計總體指標的上下限，即為總體指標m的置信水平為1-a的置信區間；

6）根據誤差傳遞公式（6）或（7）計算下氣錨后各月產液比、產油比和沉沒度比的抽樣誤差，以及下氣錨后各月產液比差值、產油比差值和沉沒度比差值的抽樣誤差。

3 影響因素

1） 置信水平的影響

置信水平是指總體參數值落在樣本統計值某一區內的概率。當抽樣井數、單井生產參數波動幅度相同時，不同的置信水平條件下的抽樣誤差 如圖1所示。

從圖1中可以看出，隨著置信水平的增加，抽樣誤差呈上升趨勢，置信區間隨之擴大。

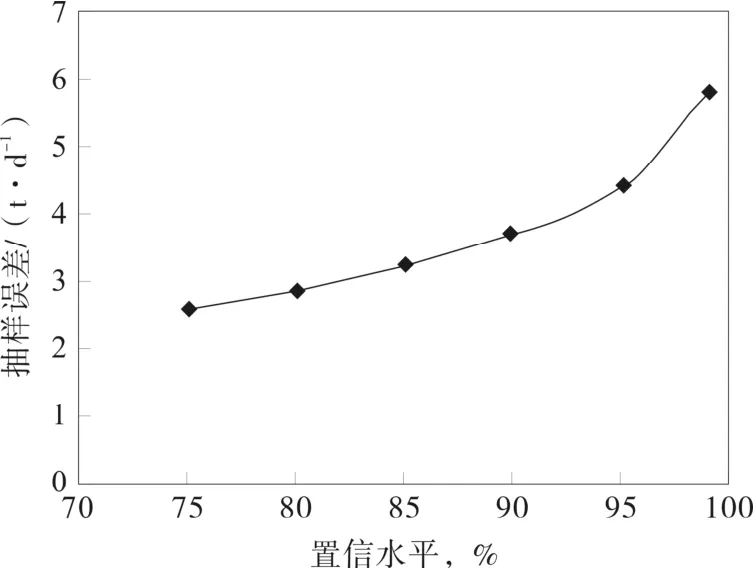
圖1 抽樣誤差與置信水平關系變化曲線Fig.1 Relationship between sampling error and confidence interval

2）抽樣測量井數的影響

當置信水平、單井生產參數波動幅度相同時，不同的抽樣測量井數條件下的抽樣誤差Dx如圖 2所示。

從圖2中可以看出，隨著抽樣測量井數的增加，抽樣誤差呈下降趨勢，置信區間隨之縮小。若抽樣測量井數越多，樣本結構就越接近總體結構，樣本對總體的代表性就越高。

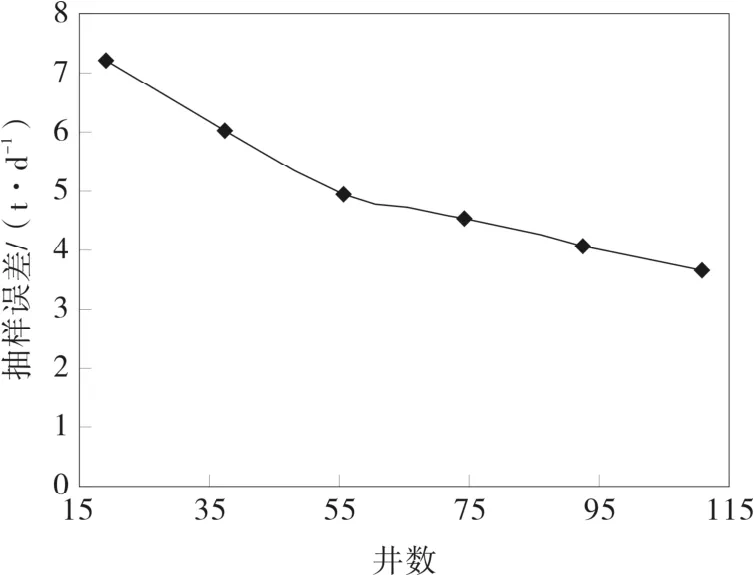
圖2 抽樣誤差與抽樣測量井數關系變化曲線Fig.2 Relationship between sampling error and numbers of sampling measurement wells

3）單井生產參數波動幅度的影響

單井生產參數波動幅度是指下氣錨后各月的產液量、產油量和沉沒度數據與其樣本平均值之間的差值，用來衡量樣本數據的波動大小。當置信水平、抽樣測量井數相同時，不同的單井生產參數波動幅度條件下的抽樣誤差Dx如圖3所示。

從圖3中可以看出，隨著單井生產參數波動幅度的增加，抽樣誤差呈上升趨勢，置信區間隨之擴大。

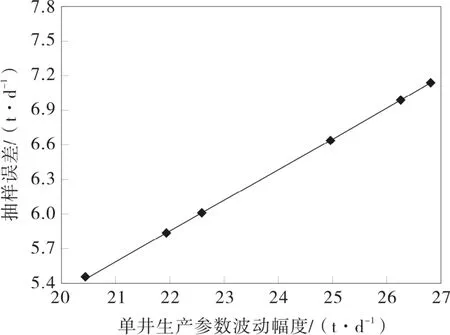
圖3 抽樣誤差與單井生產參數波動幅度關系變化曲線Fig.3 Relationship between sampling error and single well production parameter fluctuations

4 計算實例

根據多杯等流型氣錨應用試驗效果抽樣誤差和置信區間的理論基礎和數值計算方法，在設定置信水平為 90.0%的條件下，計算某采油廠下入多杯等流型氣錨后的產液量、產油量、沉沒度的抽樣誤差及其置信區間，如表1所示，從而實現某采油廠多杯等流型氣錨應用試驗效果統計誤差評價。

表1 190口氣錨井日產液量、產油量、沉沒度數據的抽樣誤差Table 1 The sampling error of average daily fluid production, oil production and submergence of 190 anchor wells

5 結 論

1）給出了多杯等流型氣錨應用試驗效果抽樣誤差與置信區間的理論基礎與數值計算方法；

2）分析了置信水平，抽樣測量井數，單井生產參數波動幅度對多杯等流型氣錨應用試驗效果抽樣誤差的影響規律；

3）根據上述計算方法，計算了某采油廠 190口氣錨井第一個月平均日產液量、產油量、沉沒度的抽樣誤差及置信區間，從而實現了多杯等流型氣錨應用試驗效果統計誤差評價。

［1］羅文銀，牛瑞云，張繼峰，等. KPX系列井下偏心氣體分離器[J]. 石油機械，2003，31(3)：29-37.

［2］辜志宏，沈磊. 井下油水分離與回注雙作用泵抽油系統[J]. 石油機械，2001，29(6)：52-54.

［3］工連習，李志升，李際瑞. 偏心氣錨的研制及應用[J]. 石油礦場機械，2003，32(1)：43-44.

［4］薄啟煒，張琪，林博，等. 螺旋式井下油氣分離器設計與分析[J]. 石油機械，2003，31(1)：8-10.

［5］李原記，朱杰，張立舉，等. 賈敏式篩離氣錨的研制[J]. 石油機械，2004，32(8)：59-60.

［6］楊建華，工春蒲，馬新民，等. 旋流式氣錨的設計與應用[J]. 石油礦場機械，2004，33(增刊)：77-78.

［7］王研，苗新蕾，崔海清，等. 多杯等流型氣錨的脫氣效率分析[J]. 大慶石油學院學報，2007，31(4)：32-36.

［8］高永久. 樣本均值作為總體均值估計量的合理性[J]. 長春理工大學學報，2008，31(4)：158-159.

［9］盛驟，謝式千，潘承毅. 概率論與數理統計[M]. 北京：高等教育出版社，2000:191-207.

［10］鄧建中，劉之行. 計算方法[M]. 西安交通大學出版社，2001:10-25.