微積分中“以直代曲”思想及其應用探析

童琳

摘 要 任何學科都有其自身的規律和特點。微積分在解決問題時的思想和方法有其獨特之處。蘊涵著豐富“轉化”的數學內涵，其中“以直代曲”的方法是微積分的重要思想，也是一種重要的處理問題的方法。本文著重分析“以直代曲”思想的特點及所蘊含的辯證因素，說明它在解決問題方面的優勢，并聯系實際說明在運用中，應充分地把握好這一思想。

關鍵詞 “以直代曲” 數學應用 微積分

中圖分類號：O172文獻標識碼：ADOI：10.16400/j.cnki.kjdkz.2015.10.027

"Replace Curve by Straight Line" Thought and its Application in Calculus

TONG Lin

（College of Education Sciences， Chengdu University， Chengdu， Sichuan 610106）

Abstract Any discipline has its own rules and characteristics. Calculus in ideas and methods to solve problems has its own uniqueness. Contains a wealth of "transformation" of mathematics content， including "straight on behalf song" approach is an important ideological calculus， is also an important way to deal with the problem. This paper analyzes the characteristics of the "straight on behalf song" Thought and dialectical factors inherent， that it advantage in problem solving， and practical instructions in the use of contact should fully grasp the idea.

Key words "Replace curve by straight line"; mathematics application; Calculus

0 前言

直與曲本來是一對矛盾，但在一定的條件下可以轉化。在微積分中直與曲充分體現了辯證法的對立統一的思想。通過微積分的學習，可以讓學生充分體會感悟“以直代曲”的思想。而這也是處理許多實際問題的基礎。例如，它是進行近似計算的基礎。對這一思想方法的把握是進行有效運用的前提。也使得一些復雜的計算在誤差要求的范圍內變得簡單可行。

1概念的界定

中國古代劉徽在運用“割圓術”求圓的周長時，在圓內作正多邊形，用多邊形的周長近似代替圓的周長，隨著邊數的增加，正多邊形的周長也越來越接近于圓的周長。劉徽通過此推導出了求圓的周長的公式。這是最早出現的“以直代曲”的例子。“以直代曲”思想，在幾何上，就是用直線或者直線段來近似代替曲線或者曲線段。從而可以利用直線的某些性質來研究曲線的某些性質。這樣將問題轉化為已知問題來解決，進而簡化計算量和使思維更加簡單。①

2“以直代曲”思想中所蘊含的辯證因素

2.1 初等數學中矩形法解題回顧

下面我們來看一下在初等數學中幾何法解題的矩形法。如果有兩個量的積剛好等于另一個量。例如，在勻速直線運動中，路程等于速度與時間的積。對比矩形的面積求法，矩形的面積等于長與寬的積。因此，若以矩形長表示時間，寬表示速度，則矩形的面積就剛好可以表示成路程。類似地，在工程問題中，工作總量等于工作效率與工作時間的積。因而工作總量也可用矩形的面積來表示。

推廣到一般，我們知道兩個量之間的關系若能抽象出函數關系，并能作出其函數圖象（有些函數不能用圖像表示）。則其函數曲線與軸所圍成的曲邊梯形的面積往往可以表征很多有實際意義的量。這可以理解定積分的概念為什么一開始要從求曲邊梯形的面積引入。也使得求曲邊梯形的面積有了更一般的意義。

2.2 定積分中求曲邊梯形的面積

在定積分的概念中，求曲邊梯形的面積。具體來說是由“分割、代替、求和、取極限”這四個步驟來完成的。

分割，首先將定義區間進行任意分割為個有限的子區間，相應地將曲邊梯形細分成個小曲邊梯形（如圖1）。

代替、求和，在上面基礎上，再將每個子區間長度乘該子區間上某點的函數值，即將每個小曲邊梯形的曲邊看作直邊（“以直代曲”），將每個小曲邊梯形近似代替成小矩形。并寫出其和式。

取極限，通過對和式取極限來求出曲邊梯形的面積。

上面過程中，分割的目的是在局部實施“以直代曲”，即以小矩形面積計算代替小曲邊梯形面積，并結合“逐次逼近”的方法來進行計算。

2.3 在微積分中，“以直代曲”的思想充分揭示了對立統一關系，以及矛盾在一定條件下可相互轉化的辯證思想

在微積分中存在著“直”與“曲”的矛盾，而處理的方式是“以直代曲”（化曲為直）。微積分中“以直代曲”的思想即是，利用微元法進行分割，再在局部實施“以直代曲”，用較規范的圖形處理一般非規范性的一般問題來解決。再進行“逐次逼近”處理問題。通過這一過程實現了“直與曲”、“近似與精確”、“有限與無限”的轉化。這也說明了矛盾在一定的條件下可以互相轉化。

數學的思想方法是學習數學的基礎。在一元微積分中，以勻速代變速，反映在幾何上就是“以直代曲”，代數上就是用“線性”代替“非線性”。從這里可以看出，中小學中幾何解法中的“矩形法”，實際是可以看成是為求定積分學習埋下的伏筆。“曲”與“直”的轉化是建立在無限分割的基礎之上的。正因為如此，在解決求平面圖形的面積、旋轉體的體積以及多元函數問題時時我們可以用“微元法”使用“以直代曲”的方法來處理。

3 “以直代曲”思想的運用

3.1函數的線性化

“在數學上最容易處理的函數是線性函數，借助于微分可使一大批非線性函數在局部轉化為線性函數，使我們在處理問題時達到簡單、方便、高效的目的。”②

在學習了微分以后，當我們從算式= ·+ （ ），得到 ≈。也即實現了函數的線性化，即有≈（） + （）（）。由此得到（） = （） + （）（）。

在幾何上，就是用過處的切線上與有相同橫坐標的點近似代替曲線上的點。從而可以比較方便地求出在曲線上附近點的函數值。

這給計算一些復雜函數的函數值（在精度要求的范圍內）找到了一種簡潔算法。這也是高等數學處理問題一種好方法，在局部范圍內“以直代曲”，用近似值代替精確值的方法。這樣達到一個將問題簡化的目的。在這里曲與直的辯證關系得到了充分的體現。同樣在學生學習了二元函數的微分以后以切平面上的點近似代替曲面上的點，這也可看成函數線性化問題的拓展。

3.2 求曲邊形的面積以及曲柱體的體積

在微積分中這種思想的運用是很多的。定積分的概念、線性化、切平面以及求曲線的長度、圓臺側面積、旋轉體體積，以及變力作功等，都直接用到了“以直代曲”的思想。

知道數學的運用并學會運用，是培養大學生的學習興趣的一個切入點。學生對數學產生了興趣，才會有數學的更好地應用。實質也是建立數學模型的問題。

例如，運籌學是一門很重要的學科，而其中扮演重要角色的一個就是線性規劃。線性規劃是運籌學的重要分支，它是一門實用性很強的應用數學學科。隨著計算機技術的發展和普及，線性規劃的應用越來越廣泛。它已成為人們為合理利用有限資源制訂最佳決策的有力工具。③

這也符合直線方程比曲線方程簡潔，計算量小。從曲線改畫成直線容易的特點。

3.3 求曲線長

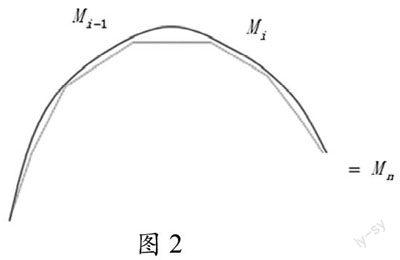
在微積分中求曲線的長，解決問題的思路，是在曲線上任意插入N個點，用線段將這些點順次聯結起來，用折線去逼近曲線上的弧段。若當折線段的最大邊長→0 時，折線的長度趨向于一個確定的極限，則稱此極限為曲線弧 AB 的弧長，即 = ∣∣（如圖2）。

由上看到，“以直代曲”的思想起了很大的作用，而“以直代曲”這只是近似，而要實現由近似到精確就要用到取極限。

事實上，物理學上我們計算變力作功、液體中的壓力、物體的轉動慣量等非均勻分布的問題，都用到了“以直代曲”思想來解決問題。

4在數學的應用中感悟“以直代曲”的思想

思考是把知識變化為智慧的催化劑。因而在數學的實踐和運用中，可以使這一思想認識更為深刻，反過來促進知識向縱深發展。大學數學學習的一個很重要的作用是要培養學生的應用意識。數學應用能力的培養是數學教育的最高目標。大學數學教學應該讓學生看到數學理論知識的運用。并培養學生的主動應用意識。

4.1 注意函數式所表征的實際意義

在數學的應用中經常要求函數的改變量，而往往直接去求計算難度較大。我們設法將 表示成 的線性函數，即線性化，從而把復雜問題化為簡單問題。微分就是實現這種線性化的一種數學模型。

例如，在學習了微分以后，學習函數的線性化，就是用過處的切線上與有相同橫坐標的點近似代替曲線上的點。

反過來，在我們學習了函數的線性化以后，我們再回過頭來看公式= ·+ （ ）

就更能理解為什么把· 稱為 線性主部的意思了。這也給求一個函數的近似值提供了理論依據。

4.2 借助幾何直觀深刻領悟“以直代曲”的思想

例如，對于二元函數的線性化公式，我們可以畫出它的切平面來理解其意義。即在數學教學和運用中讓學生去感受“以直代曲”的思想，去欣賞數學的簡潔之美。并主動去運用這種方法。事實上，在微積分中“以直代曲”的思想還有很多，例如，以勻速代變速等等。有了“以直代曲”思想的學習，也為學生學習“以曲代曲”的思想打下了基礎。例如，函數的泰勒公式。即是用一條多項式所表征的曲線去代替另一條曲線。

通過微積分的學習，培養學生形成數學的思維模式。并讓數學的內容和方法滲透到應用中去。不斷增強學生的數學建模能力。并在通過此感受數學的本質。

注釋

① 趙健寶，李娜.“以直代曲”思想來看一類等價無窮小[J].邢臺學院學報，2013（6）.

② 張順燕.數學的思想、方法和應用[M].北京：北京大學出版社，2003：196.

③ 張干宗.線性規劃[M].武漢：武漢大學出版社，2007-03-01.