讓“好題”照亮學路

葉柱

葉 ?柱 中學高級教師，浙江省紹興市上虞區教學研究室小學數學教研員，全國人教版課改實驗優秀教師，浙江省特級教師，浙江省教育學會小學數學分會學術委員，浙江省中小學教材學科審查委員會委員，浙江省紹興市名師培養工程導師，紹興市學科帶頭人，紹興市十佳青年教師標兵，紹興市教科研先進個人。

自1994年參加工作以來，潛心課堂，鐘情教研。曾獲“浙江省第十屆小學數學優質課評比”一等獎、“華東六省一市第十屆小學數學優質課評比”一等獎、“中國教育學會小學數學教學專業委員會第十二屆優秀論文評選”一等獎。150余篇學術論文公開發表，個人專著《數學教學新視界探真》由浙江大學出版社正式出版，主編或參編教學用書近百萬字。

無論哪個學段，題目始終是數學學習的重要資源。學生在“例題”的研探中體驗、在“習題”的操練中內化、在“試題”的測評中反思，從而夯實了學科基礎、領會了數學思想、積累了學習經驗。波利亞曾經強調：“一個專心的認真備課的教師，能夠拿出一個有意義但不復雜的題目，去幫助學生挖掘問題的各個方面，使得通過這道題，就好像通過一扇門，把學生引入一個完整的理論領域。”確實，題目品質的優劣直接影響著學習效果的好壞。作為一名數學教師，理應多給學生提供“有意義但不復雜”的“好題”，為其數學建構提供絕佳的載體、打開寬綽的空間。下面，筆者就新理念下小學數學“好題”的基本屬性談些思考。

一、“好題”，是有情趣的

數學題應有情趣，其道理是顯而易見的。正如《義務教育數學課程標準》（2011年版）所指出的：“課程內容的選擇要貼近學生實際。”數學題的設計也要貼近學生“未成年狀態”的實際，力求順應童真、趣味盎然。但是，有一種現象亟須引起警惕。有些教師為了追求情趣性，在題目旁邊配上一些諸如“孫悟空”的卡通形象，就美其名曰“讓我們和孫悟空一起解決問題”，而具體的題目信息及解答過程則與孫悟空毫不沾邊。在這里，數學題的情趣性被狹隘地理解為“裝飾”與“噱頭”。由此，會使學生受到淺層刺激的外部干擾，從而影響主體思考的精度和深度。所以說，“好題”的情趣，絕不等于“加點花頭”“弄點幌子”，而是通過營造貼近兒童心理的問題情境，將需要落實的目標點以學生喜聞樂見的生動方式呈現出來，激發學生“親近題目”的熱情與“一探究竟”的欲求。

例如，全國各版本數學教材編寫時都強調“對話”形式，即通過人物之間的交流分享，生成問題，提煉策略，明晰知識。“對話”是人們參與現實生活的重要方式，也吻合學生樂于表現的年齡特點。為此，我們可以借鑒教材的編寫特點，設計“對話”形式的數學題，為解決問題預設一條“抽絲剝繭”的探究之路，由此凸顯題目的內涵與情趣。

【題例1】“除數是一位數的口算除法”原創題（人教版三年級下冊）

三位小朋友同時在口算一道“除數是一位數的除法題”。根據他們的想法，你覺得，這道除法題是（）。

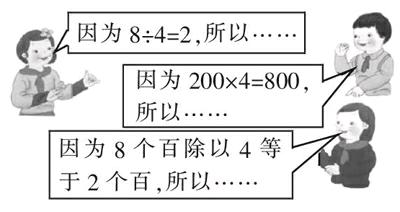
此題呈現了三個小朋友不完整的話語信息，給學生創設了一個“他們究竟在口算哪道題呢”的“破案”場景，顯得饒有趣味。每個小朋友的話語信息，恰好對應了“除數是一位數的口算除法”的一種算法，所以通過“破案”活動，學生在不知不覺中有序梳理了口算除法的三種算法。另外，根據一個小朋友的話語信息還不足以揭示真相，如針對第一個小朋友所說的“因為8÷4=2，所以……”，能夠聯想到80÷4、800÷4、8000÷4等很多算式，但綜合三人的所有信息便能鎖定“800÷4”這一正解。這個過程，利于學生推理能力的提升。顯然，此題之所以是“好題”，是因為它突破了常規題目“根據算式想方法”的定勢，彰顯了“基于方法尋算式”的新意，真正打開了主動探求、積極思考的情趣性學習空間。

二、“好題”，是有意圖的

題目的價值，是促進學生的數學發展。因此，通過每道題的解答，具體促進學生哪個方面的數學發展，這是教師需要時刻關注的。真正的“好題”，并非信手拈來、隨意亂用的，而是需要精心設計、適時巧用的。比如，上面的題例1，在其情趣性表象的背后，“幫助學生有效建構口算除法的三種算法”的訓練意圖是清晰而堅定的。所以，我們必須以“四基”理念為宏觀導向，以教材要求為基本線索，細化訓練目標，明晰訓練落點，設計出指向準、意圖明的數學題，來助推學生的數學發展。在當前深化課程改革的背景下，“好題”的意圖在以下兩個方面尤其要凸顯。

其一，夯實意義理解

很多老師都有同感，學生解題的重要意義在于“熟能生巧”。但在筆者看來，這里的“熟”所指向的，不應僅僅是“方法表象”及“答題套路”，更應包括“策略原理”與“意義本質”。只有完滿的“熟”，才能生成深度的“巧”。因此，教師在設計題目時，要適時革新“老面孔”、拆除“老包裝”、打破“老思路”，在聚焦知識核心不動搖的前提下，加強變式，盤活結構，來喚醒學生對知識內涵的舊理解，促進學生對數學意義的新感悟。

【題例2】“確定位置”原創題（人教版五年級上冊）

如圖，在直角三角形ABC中，頂點A的位置用數對表示是（10，16），頂點B的位置用數對表示是（8，12），那么，頂點C的位置用數對表示是（ ?）。

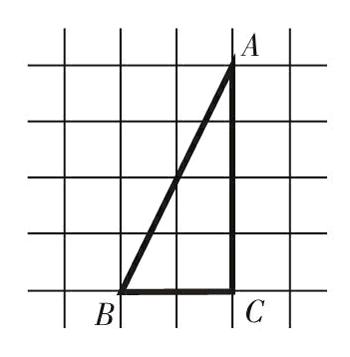
很多關于數對的題，都是給出完整的坐標信息，讓學生寫出指定位置的“數對”。幾次練習后，學生對“數對中前面的數表示列、后面的數表示行”便很清楚了。然而，要幫助學生深度建構“數對”的意義，光憑此類僅靠模仿就能解決的基礎題是不夠的。此類題目所含的思維空間較窄、探究張力較小，所以，知識意義在學生腦海中的植入度便較低。相比而言，本題有些“不按常理出牌”，隱掉了完整的坐標信息，讓學生根據A、B的位置來推斷C的位置。在“走迷宮”式的任務情境中，為確定C的位置，學生必然需要自覺解讀表示A、B位置的“數對”。而這個解讀的過程，就是對“數對”意義的再理解過程。隨后，學生會發現C與A同列、與B同行，所以列數與A相同，行數與B相同，由此得出C的位置是（10，12）。這個過程，凸顯了對“數對”構成的意義理解，有力拓展了認知深度。

【題例3】“小數乘法”原創題（人教版五年級上冊）

學習小數乘法時，我們知道了：“因數中一共有幾位小數，就從積的右邊起數出幾位，點上小數點。”那么，為什么因數中有幾位小數，積就是幾位小數呢？請以3.76×0.4=1.504為例，說說你的想法。

這道題選自筆者命制的一份區域性質量調測卷，其檢測視點在于，學生是否理解了小數乘法的算理，并能用自己的方式清晰表達。如果說，題例2指向的是對知識本身（數對）的意義理解，那么，本題所指向的則是對知識來歷（算理）的意義理解。像這樣的題目，在“偏重知識運用、忽視原理建構”的傳統教學中是極其少見的。從答題情況看，學生之間的差異很大。有些學生能像教材例題那樣，以圖示、文字等方式呈現“兩個因數先看作整數相乘再將積縮小”的動態過程，比較清晰地揭示“積的小數位數”的形成真相;有些學生則備感茫然，寫出的答案是“這是一種規定”“老師就是這樣告訴我們的”“算起來比較方便”……不同形態的回答所折射出的，是學生對算理理解的真實水平，以及教師教學行為的客觀樣貌。當前，應該適當加強此類“聚焦原理解讀”題目的比重，來引領學生的學與教師的教。

其二，錘煉核心能力

《義務教育數學課程標準》（2011年版）提出了數學課程十大核心詞：數感，符號意識，空間觀念，幾何直觀，數據分析觀念，運算能力，推理能力，模型思想，應用意識，創新意識。對此，我們也可以理解成，數學課程亟須培養學生這十種核心能力。對于這些核心能力的教學，教師不能停留在觀念上、口頭上，應落實到行動上（包括題目設計）。也就是說，教師在設計數學題時，應結合具體的教學內容，有意識地將這十種核心能力的檢測及錘煉融入其中。由此，既鞏固了基礎知識，落實了基本技能，又使核心能力的養成落到實處。

【題例4】“圖形的旋轉”原創題（人教版五年級下冊）

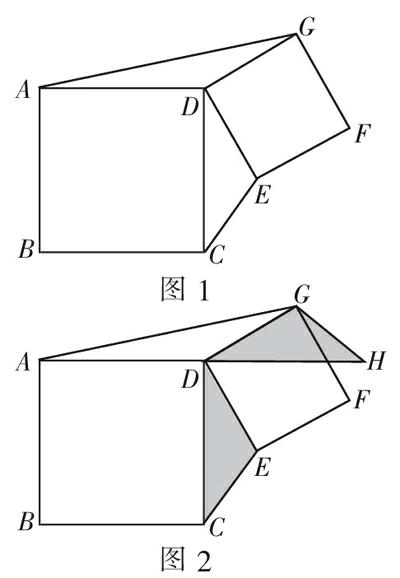
如圖1，四邊形ABCD和四邊形DEFG都是正方形。三角形ADG的面積是10平方厘米，則三角形DCE的面積是（ ?）平方厘米。

乍看此題，似乎信息不全，無從下手。事實上，此題為“空間觀念”“應用意識”預留了寬綽的“用武之地”。如果學生能夠想到將三角形DCE繞D點逆時針旋轉90°，問題便可迎刃而解。如圖2，圍繞D點，線段DC旋轉到了DH的位置，線段DE旋轉到了DG的位置（DE與DG原本就是正方形的兩條邊），三角形DCE整體旋轉到了三角形DHG的位置。而三角形DHG與三角形ADG等底等高，所以三角形DCE與三角形ADG面積相等，即10平方厘米。這道題中，“將一個三角形逆時針旋轉90°”是基本知識點。在一個比較復雜的面積計算情境中，能否想到“通過旋轉，尋求關聯”，是對學生“空間觀念”“應用意識”的有力挑戰。經歷解答過程后，學生不僅能對“旋轉究竟有什么用”產生切身體會，其空間想象能力也會得到有益提升。

當然，指向核心能力錘煉的數學題并非“高大上”。很多時候，我們只需要在常規題目的基礎上“跟進一步”即可。

【題例5】“長方形、正方形的面積計算”原創題（人教版三年級下冊）

1.算一算：下面圖形的面積各是多少？

圖3：長4分米、寬3分米的長方形

圖4：長28米、寬15米的長方形

圖5：邊長6厘米的正方形

2.想一想：生活中，這三個圖形的大小分別接近于哪個物體的表面呢？請連線。

圖3 ? ?圖4 ? 圖5

魔方的一個面 ?電腦屏幕籃球場

此題中，“算一算”部分屬于常規性的面積公式運用，在后面添上“想一想”部分，整道題的立意便被拉高了：引導學生立足基本操練、拓寬認知視野，尋找每個面積的生活原型。在這個過程中，量感得以鞏固，應用意識也由此切實強化。

三、“好題”，是有效度的

在力求創新、追尋“好題”的過程中，我們需要始終關注一道“好題”的底線屬性：效度。根據“百度百科”的定義，效度是“測量工具所能測出其所要測量特質的程度”。也就是說，題目作為“工具”，用其測量后，所能呈現出的原先想要反映的訓練目標或檢測目標的程度，即為效度。由于命制過程的種種缺失，當下題目效度缺失的現象并不鮮見。日常教學中，一些題目之所以會引起爭論，“效度缺失”便是重要原因。為了確保效度，我們在設計題目時務必遵守兩條準則。

其一，要緊扣課程要求

前文談到，“好題”是有意圖的。這個意圖，必定依托“課標精神”“教材要求”而確立。在此基礎上，從“題目材料的選擇”，到“題面信息的形成”，再到“題解思路的預設”都要與測量意圖高度匹配。切忌出現有悖于課標要求的內容細節，以免影響題目效度。

【題例6】“左右”測試題（人教版一年級上冊）

此題選自某校一年級上學期的一份單元測試卷。有的學生以自己（觀察者）為參照點，填了“4”;有的學生則以小紅（活動者）為參照點，填了“2”。閱卷時，老師們也展開了廣泛討論。筆者認為，命題者沒能把握課標關于第一學段“左右”教學的具體要求：強調以“學生身體”（即“左右手”）為中心辨識左右。而且，《教師教學用書》強調：教師應慎重對待位置關系的相對性問題，不能任意提高教學內容的難度。審視本題，我們不難發現，“小朋友排隊”的材料適合于考查“前后”，不適合于考查“左右”。如果非要用這則材料來考查“左右”，必須讓小紅轉過身去，與其他學生身體朝向一致，避免“相對性”帶來的難度。由此，題目才能更為真實地檢測出每名學生“以自我身體為中心辨識左右”的能力水平。

其二，要避免思維歧義

當前，很多教師都注意了將數學題目與生活場景結合起來，從中體現現實性與應用味，這當然是非常正確的。不過，在充分把握生活資源對數學理解的重要意義的同時，我們也要注意生活經驗可能會對解題思路造成的客觀干擾，要更為嚴密地編制題目，確保測量結果的效度。

【題例7】“小數的大小比較”作業題（人教版四年級下冊）

下表是五位同學的跳遠比賽成績。

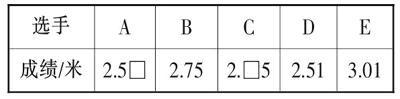
如果C至少是第二名，那么，他跳了（ ?）米。

此題順應了學生熟悉的“跳遠比賽”情境，將“小數的大小比較”融合其中，且任務設置富有探究性，將“推理能力”的訓練落到實處，確實是一道“好題”。不過，有位學生的解答引起了筆者的思考。別人的答案都是“2.85”（這應該是命題者預設的正確答案），可該生卻堅持“2.75”。他的理由是：“題中寫著‘至少，那就是說數據要盡量小一些。而C和B‘并列第二名時C的數據是最小的。所以，我認為是2.75米。”你能說這個學生的意見沒道理嗎？生活中，確實存在“并列名次”這回事兒。生活經驗告訴他，要實現“至少”，就很有可能是“并列第二名”。這樣一來，“2.85”“2.75”兩個答案皆有其合理性了。其實，如果命題者將C的成績調整為“2.□3”（百分位不是“5”皆可），可能答案就唯一了。