基于小波MFCC與HMM的列車鳴笛識別算法研究

蔣翠清，李天翼

（合肥工業大學 管理學院，合肥 230009）

基于小波MFCC與HMM的列車鳴笛識別算法研究

蔣翠清，李天翼

（合肥工業大學 管理學院，合肥 230009）

本文提出了一種列車鳴笛識別方法，用更能反映出聲音信號特征的梅爾倒譜系數（MFCC）特征作為列車鳴笛識別的參數，同時，用小波變換替代MFCC參數提取過程中的FFT變換，將改進后的MFCC參數與隱馬爾可夫模型（HMM）結合，獲得比LPCC特征或MFCC特征更好的識別效果，并通過仿真實驗對比驗證了該算法的有效性和可行性。

列車鳴笛識別；梅爾倒譜系數；小波變換；隱馬爾可夫模型

1　引　言

列車鳴笛識別的基本原理是從實時采集的列車聲數據中，提取能反映其特征的參數，與列車行進過程中的典型聲音（鐵軌摩擦聲、剎車聲等）建立的模型匹配，得出識別結果。利用這種技術可實現列車鳴笛自動檢測，以促進列車乘務員加強對列車信號及前方進路的瞭望確認，對列車乘務員是否瞭望確認進行監督。

語音信號識別常用的特征參數有線性預測系數、線性預測倒譜系數（Linear Prediction Cepstral Coefficients，LPCC）和Mel頻率倒譜系數（Mel Frequency Cepstral Coefficients，MFCC）等。其中，MFCC模擬了人耳耳蝸的聽覺特性，在語音識別領域得到了廣泛應用。文獻提取了聲音信號的MFCC參數進行聲音識別，取得了一定的效果，但列車聲信號是不平穩的，MFCC無法很好地反映其特性。小波變換能夠精確的表征非平穩信號的變化，并且其特性與人耳耳蝸的生理頻率響應特性相似。用小波變換來改進MFCC特征提取，能精確地反映列車聲信號的動態特性，因而采用改進后的MFCC作為列車聲信號的特征參數更好。

隱馬爾科夫模型（Hidden Markov Model，HMM）是一個時間序列模型，一個無記憶的非平穩隨機過程，表征時變信號的能力很好，可以處理聲音信號中所包含的時序信息和統計信息，已經被廣泛應用于語音建模。

文中提出了一種基于小波MFCC參數和HMM模型的列車鳴笛識別方法，選取改進后的MFCC參數作為特征，由實驗數據分析證明了該鳴笛識別方法的可行性。

2　聲音特征參數選取

聲音特征參數提取是指從列車聲信號當中獲得能夠描述音頻信號特征的過程。

2.1MFCC參數的提取

MFCC參數在語音信號識別領域運用極為廣泛，它結合了語音的產生機制和人耳的聽覺感知特性，能夠很好地反映語音信號的特性，從而提高算法的識別率。如圖 1 所示，在正常提取MFCC參數的過程中對信號要作快速傅里葉變換。

圖1　MFCC參數提取流程

2.2離散小波MFCC參數的提取

傳統的Mel頻率倒譜系數假設聲音信號是短時平穩的，用固定窗的傅立葉變換獲得。由不確定性原理可知這種假設會使聲音的頻譜細節特征模糊，丟失一定的信息。并且MFCC無法反映非平穩列車聲信號的瞬間變化，因此，傳統的MFCC系數在列車鳴笛識別算法中不能收到很好的效果。用離散小波傅里葉變換改進傳統MFCC參數提取過程中的快速傅里葉變換，能夠較好地解決上述問題。

小波變換采用多分辨力分析的思想，非均勻地劃分時頻空間，與人耳蝸的頻響特性相似。因此，在使用離散小波傅里葉變換的情況下，列車行進聲信號在時頻域都可獲得了較為合適的分辨能力。實驗中采用離散的二進制小波，其表示式為：

式中，f（t）為能量有限信號；φm，n（t）為二進制小波，表示式為：

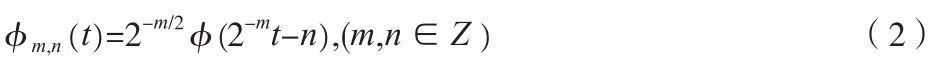
用離散小波傅里葉變換改進傳統MFCC系數提取過程，得到新的特征參數——小波MFCC系數（記作WMFCC）。WMFCC系數的提取過程如圖2所示。

圖2　WMFCC參數提取流程

3　隱馬爾可夫模型

隱馬爾可夫模型是語音處理中廣泛應用的一種統計模型。HMM是一個雙內嵌式隨機過程，其中，一個隨機過程描述狀態的轉移，另一個隨機過程描述觀察值和狀態之間的統計對應關系。

HMM可以用一個五元數組：λ=（P，Q，a，M，N）描述，其中P為模型中狀態數目，Q為每個狀態可能的觀察值數目，a表示初始狀態概率，M表示狀態轉移概率矩陣，N表示觀察概率矩陣。由于在算法識別過程中狀態數目和觀察值數目不變，HMM也可簡寫為λ=（a，M，N）。

HMM的常用算法有三種：前向—后向算法、Viterbi算法和Baum-Welch算法。本文中HMM的訓練使用Baum-Welch算法，HMM的識別使用Viterbi算法。

Baum-Welch算法可描述為：給定1個觀察值序列O = O1，O2，…，OT和一個HMM初始參數λ=（a，M，N），使觀察序列O相對于λ的概率P（O|λ）最大。Baum-Welch算法為了得到模型參數的最優解，將新老HMM模型參數的函數進行迭代運算直到P（O|λ）收斂，即HMM模型參數不再變化為止。

Viterbi算法可描述為：給定1個觀察值序列O = O1，O2，…，OT和一個初始參數λ=（a，M，N），如何確定未知序列K=K1，K2，…，KT的P（K，O|λ）最大時的最佳狀態序列K*=K1*，K2*，…，KT*。對于要識別的聲音信號，可算出聲音特征通過每個HMM模型的概率P（K，O|λi），其中輸出概率最大的模型作為識別結果。HMM模型的原理如圖3所示。

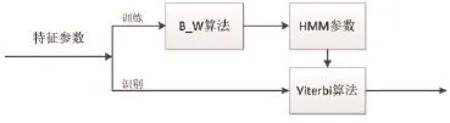
圖3　HMM模型原理圖

4　基于小波MFCC和HMM模型對列車鳴笛的識別

基于小波MFCC和HMM的列車鳴笛識別算法如圖4所示。首先，對列車聲信號樣本進行預處理，提取MFCC和WMFCC，然后一部分樣本特征作為訓練集，將兩個參數分別通過HMM模型進行訓練，以得到最優的HMM參數并存儲；另一部分樣本特征作為測試集，通過訓練好的模型識別系統計算，從而判斷其類型。

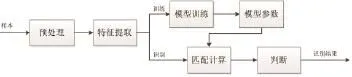
圖4　基于小波MFCC和HMM模型的列車鳴笛識別算法

5　實驗及分析

本文實驗樣本均為鐵路路口現場錄制，樣本精度為16bit，采樣率為44.1kHz。列車聲音分鳴笛和非鳴笛兩大類，鳴笛種類為電鳴笛和汽鳴笛，非鳴笛種類為鐵軌聲、風聲、剎車聲等。其中，鳴笛類聲音有120個樣本，非鳴笛類聲音樣本有200個。

本文分別提取3種參數（LPCC，MFCC，WMFCC）進行對比實驗。LPCC參數采用文獻的提取方法。MFCC和WMFCC參數的提取的過程中設置如下：信號的分幀長度取為25ms，幀移為8 ms。MFCC參數提取時數字濾波器組選24個，DCT系數為12*24維，對處理過的聲音信號進行反離散余弦變換后得12個MFCC系數，再計算其一階差分12個共24維；其中WMFCC對信號進行6層小波分解，分解后可得7層小波系數。

將實驗樣本分為訓練樣本和測試樣本：訓練樣本為樣本總數的80%，測試樣本為剩余的20%的樣本。每組實驗做10次，列出每類聲音的平均識別率，最后對不同特征組合下聲音的識別率及效率進行比較。

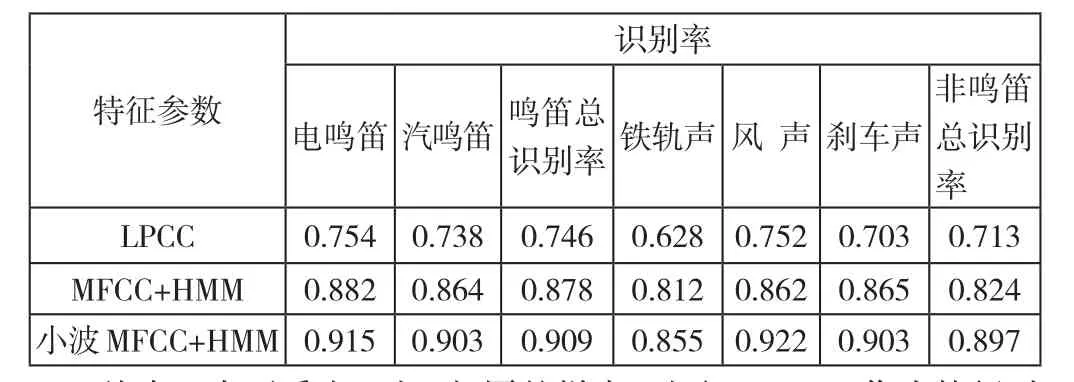
表1　不同特征參數識別結果

從表1中可看出，對于相同的樣本，選取WMFCC作為特征時的正確率比選取MFCC作為特征的正確率都要高，說明WMFCC更能反映火車聲信號的非平穩特性。從鳴笛和非鳴笛的總識別率還可以看出，選取WMFCC作為特征參數時，用HMM模型能準確分辨火車鳴笛跟非鳴笛，說明火車鳴笛與非鳴笛聲信號的WMFCC特征有著較大的差異。由以上分析可得出結論：利用小波MFCC和HMM對火車鳴笛進行識別是可行的。

6　結　論

本文將語音識別中常用的特征參數MFCC與小波變換結合，運用到列車鳴笛識別領域。提出了基于小波MFCC參數與HMM模型列車鳴笛識別方法，通過實驗的數據分析表明該方法識別率較高，在列車鳴笛等異常聲音識別中有良好的應用前景。

如果對算法進行優化，將其移植到C等底層語言中并與硬件結合，不僅能夠較大幅度地提高算法運行效率，同時還能實現列車鳴笛的實時識別，從而更好地監督列車乘務員是否瞭望確認，促進火車的安全運行。

主要參考文獻

［1］S Chauhan，P Wang，C Sing Lim，et al.A Aomputer-aided MFCC-based HMM System for Automatic Auscultation［J］.Computers in Biology and Medicine， 2008， 38（2）： 221-233.

［2］成彬彬，張海.基于小波變換的數字耳蝸濾波器組設計與實現［J］.電子技術應用，2009（1）：135-138.

［3］劉輝，楊俊安，許學忠.基于 MFCC 參數和 HMM 的低空目標聲識別方法研究［J］.彈箭與制導學報，2008，27（5）：217-219.

［4］韓紀慶，張磊，鄭鐵然.語音信號處理［M］.北京：清華大學出版社，2004.

［5］張德豐.MATLAB 小波分析［M］.北京：機械工業出版社，2009.

［6］陳韜偉，辛明.基于小波變換的雷達輻射源信號特征提取［J］.信息與電子工程，2010，8（4）：436-440.

［7］張小玫，張雪英，梁五洲.基于小波 Mel 倒譜系數的抗噪語音識別［J］.中國電子科學研究院學報，2008，3（2）：187-189.

［8］ 何強，何英.MATLAB 擴展編程［M］.北京：清華大學出版社，2002：352-371.

［9］ 王鐘斐，王彪.基于短時能量—LPCC 的語音特征提取方法研究［J］.計算機與數字工程，2012，40（11）：79-80.

10.3969/j.issn.1673 - 0194.2015.06.053

TN912.34

A

1673-0194（2015）06-0072-02

2015-02-11