Car following model with consideration of the vehicle’s mechanical inertia effect and its stability analysis

Tong ZHOU, Yu-guang CHEN, Yu-xuan LI

(1College of Information Engineering, Chongqing Institute of Engineering, Chongqing 402260, China)(2College of Computer Science, Chongqing University, Chongqing 400044, China)(3 College of Electronic Information & Automation, Chongqing University of Technology, Chongqing 400054, China)

?

Car following model with consideration of the vehicle’s mechanical inertia effect and its stability analysis

Tong ZHOU1, 2*, Yu-guang CHEN3, Yu-xuan LI1

(1College of Information Engineering, Chongqing Institute of Engineering, Chongqing 402260, China)(2College of Computer Science, Chongqing University, Chongqing 400044, China)(3College of Electronic Information & Automation, Chongqing University of Technology, Chongqing 400054, China)

In order to describe the car-following behavior more actually in real traffic, a new car following model by considering the vehicle’s mechanical inertia effect is proposed on the basis of the full velocity difference car following model. The stability condition is given by applying the control theory. The simulation results are compared with that of the previous models, and show that our model can overcome the deficiency that the acceleration of leading vehicle of motorcade instantly jumps in those models, and the traffic jam can be suppressed as the coefficient of vehicle’s mechanical inertia effect decreases. The simulation results are consistent with theoretical analysis.

Traffic flow, Traffic congestion, Car following model, Vehicle’s mechanical inertia effect

1 Introduction

In recent years, the problems of traffic jam have been widely investigated. In order to understand the mechanism and properties of traffic jam, some traffic flow models have been presented, such as car-following models, cellular automaton models, gas kinetic models and hydrodynamic models [1-4]. Among these models, the current car-following model is an effective method to study the microscopic traffic flow. It is well known that the optimal velocity (OV) model proposed by Bando et al.[5], which is one of favorable car-following traffic models, has successfully described the formation of traffic jams in a simple way. Subsequently, inspired by the OV model, some new car-following models were put forward to describe the traffic nature successfully [6-14]. Some of them were extended by introducing multiple information of headway or relative velocity [6-9], and others were considered the two factors at the same time [10-15].

These car-following models mentioned above can reproduce many complex actual traffic phenomena. However, these models cannot be used to study the complex phenomena resulted from the vehicle’s mechanical inertia effect since this effect is not considered in those models. In fact, the vehicle’s mechanical inertia can hinder the change of vehicle’s motion state, that is to say, the change of a car’s running state from one motion state to another motion state need a period of time due to the presence of the vehicle’s mechanical inertia effect rather than an instantly jump. In view of the above reasons, this research considers the influence of the vehicle’s mechanical inertia effect on traffic flow. Moreover, the present paper introduces a new car-following model considering the vehicle’s mechanical inertia effect.

The paper is organized as follows: a new car-following model is introduced in the section 2; in section 3, the stability analysis is discussed; the starting process simulation and the traffic dynamics simulation are presented in section 4; section 5 presents the conclusions.

2 Models

In 1995, Bando et al. [5] proposed an optimal velocity model (OVM), and the motion equation is given as follows:

(1)

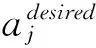
In order to overcome the deficiency, Helbing and Tilch [6] proposed a generalized force model (GFM), i.e.

(2)

WhereH(·) is the Heaviside function,λis a sensitivity coefficient, and Δvj(t) is the real velocity difference between the preceding carj+1 and the following carj. The simulation shows that the GF model is poor in the delay time of car motion. In view of the problem, Jiang et al. [7] modified the model by introducing the relative velocity, and the full velocity difference model (FVDM) was developed:

(3)

The results illustrate that FVDM has better agreement with the field data than OVM and GFM. These models mentioned above can reproduce some complex actual traffic phenomena but the models cannot be employed to study the effect of the vehicle’s mechanical inertia on traffic flow. In real traffic, the driving behavior is a process that a driver senses the information from the preceding vehicles and the ego-vehicle, and then analyzes and processes these information, and formulates an acceleration command to control his vehicle for achieving optimal state. In the possess, the acceleration command is just the driver’s desired acceleration which can change the state of the movement of his car, when it acts on the vehicle system, the desired acceleration will change to real acceleration due to the influence of the vehicle’s mechanical inertia effect. Therefore, a new car-following model considering the vehicle’s mechanical inertia effect is proposed

(4)

(5)

Where thevmax=2 is the maximum velocity andhc=4 is the safe distance.

3 Stability analyses

This paper rewrites the dynamics equation of new car following model from the perspective of the control system as follows:

(6)

(7)

To analyze the stability of steady-state solution (7), one can check the following linearization of Eq. (6) at solution (7).

(8)

The state-space expression of the new model can be obtained at the steady state (7):

(9)

From the frequency domain viewpoint, the linearized system can be written as:

(10)

WhereVj(s)=L(δvj+1(t)),Vj+1(s)=L(δvj+1(t)),L(·) denotes the Laplace transform (the Laplace transform is an integral transform perhaps second only to the Fourier transform in its utility in solving physical problems). The transform functionG(s) is given by

(11)

Where the characteristic polynomiald(s)=τλ(s3+τs2+(τk+τλ)s+τkΛ).

Definition 1 Assumingd(s) is stable, ifH∞-norm of G(s) is less than 1, that is:

(12)

the traffic jams does not occur in our model. From the analysis above, the stability condition can be obtained as follow:

(13)

When small perturbations are added to the uniform traffic flow, traffic flow is stable and robust for low density because the condition (13) holds. When the density exceeds the critical density (namely, the condition (13) is unsatisfied), the uniform traffic flow becomes unstable and makes a phase transition to a congested flow [13,14]. This paper chooses the parameters according to the simulations in reference [0] and [11], where the sensitivity coefficient of the velocity differenceλ=0.8, the gain curve of |G(jw)| can be obtained as the figure in the below. It can be seen from Fig. 1 that whenτ=1,0.6,0.4, the stability condition (13) of our model is not satisfied, |G(jw)| has a peak greater than 1, which means that the perturbation in the process of the transmission will not damp to zeros. It is noted that with the decrease of the valueτ, the stability performance of our model become better. Whenτ=0.2, the gain of |G(jw)| keeps not greater than 1 which indicates the traffic system is stable. Whenτ=0, the stability condition of our model is the same as that of FVDM.

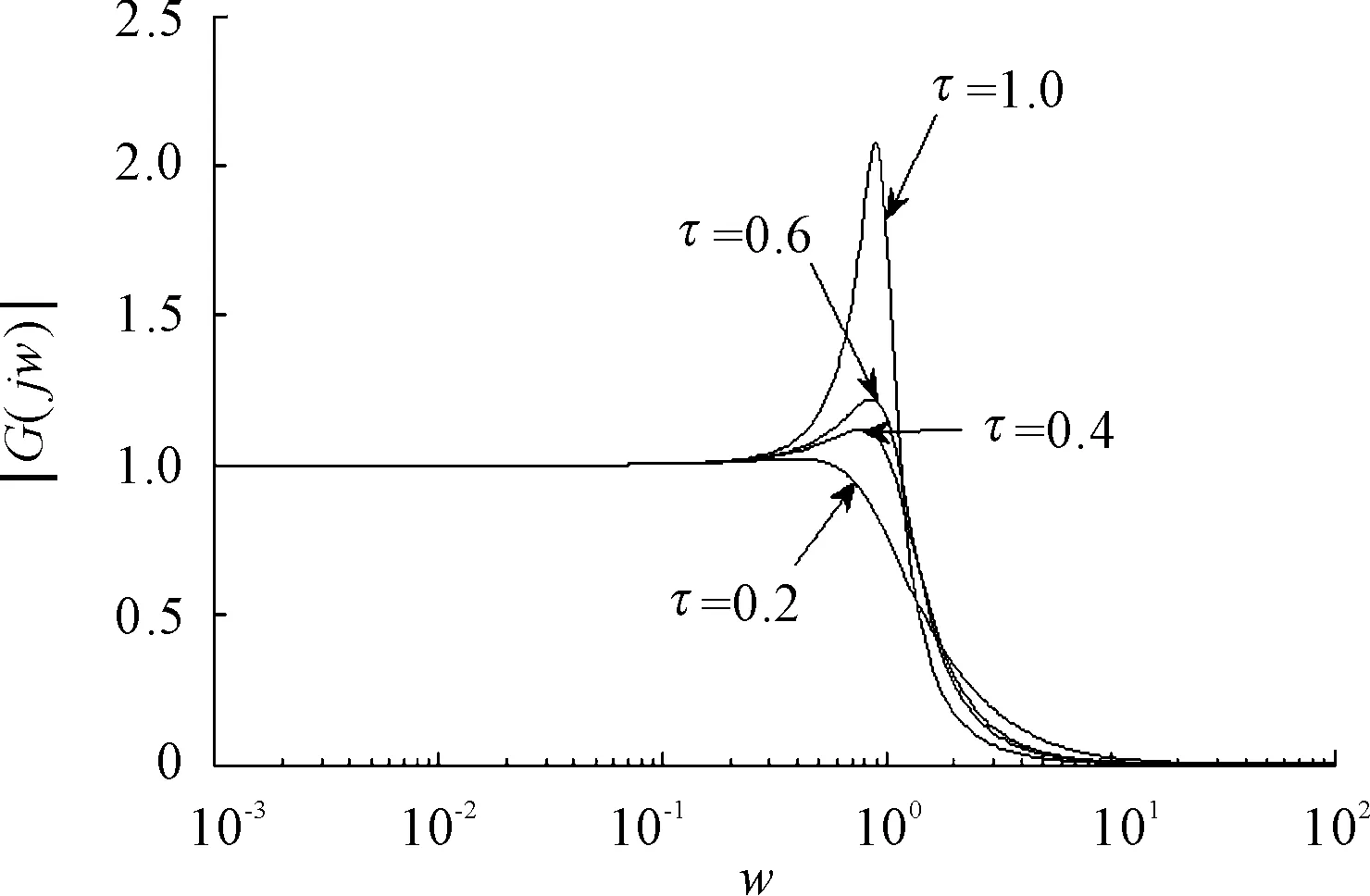
Fig.1 The gain curve of theG(s)

4 Simulation

On the basis of the stability analysis, several numerical simulations are carried out to verify the performance of the model.

4.1 The starting up process

This research carry out the starting process simulation as that in reference [6] to compare physical properties of our model with those of FVDM under a traffic signal. Firstly, the traffic signal is red and all vehicles (10 cars in the simulation) are waiting with aheadway of 7.4 m, where the optimal velocity is zero. The coefficient of the vehicles’ mechanical delay chooses asτ=0.2. Then, the signal changes to green and vehicles start to move. The simulation results of these two models are shown in Fig.2 and Fig.3.

From Fig.2, it can be found that when 10 vehicles start to move, the phenomenon that the leading vehicle’s acceleration instantly jump does not appear in traffic system. The acceleration of unobstructed leading vehicle of our model changes slowly, and the maximum acceleration of the leading vehicle of our model is lower than that of the FVDM at the beginning time since our model considers the vehicle’s mechanical inertia effect. In Fig.3, the velocities of the 10 vehicles in our model slowly increase to stable velocity, and the delay time of vehicles is bigger than that of FVD model. The simulation results show that the vehicle’s mechanical inertia effect plays an important role in the vehicle dynamic driving behavior.

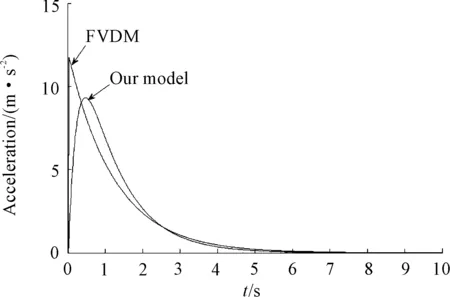
Fig.2 The acceleration of unobstructed leading vehicle in two models

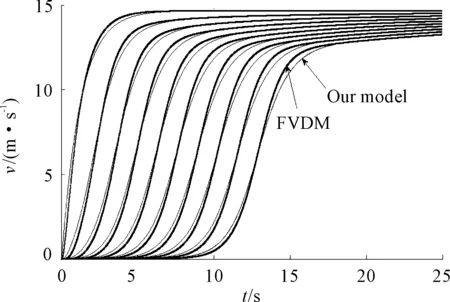
Fig.3 Motion of vehicles 1-10 starting from a traffic signal for FVDM and our model

4.2 Verification of the stability analysis

Now a numerical simulation is carried out to check the stability analysis and verification of the traffic phenomenon under a periodic boundary condition, the optimal velocity function is chosen as in [0]. The parameters are chosen asτ=0.5,k=0.41 andλ=0.8. It is assumed that there areN=100 cars running on the road with the lengthL=1 500 m,and the initial disturbance is the same as that in Ref. [7].

Fig.4 shows the space-time evolution of the velocity aftert=0 time steps under the different parameterτ. The patterns (a)-(d) in Fig.4 exhibit the time evolution of the velocity forτ=1,0.6,0.4,0.2 respectively. In patterns (a)-(c), it can be seen clearly that the traffic flow is unstable and the speed fluctuation appears because the linear instability condition (14) is unsatisfied. At the same time, with the value ofτincreasing, the amplitude of velocity fluctuation will be amplified gradually with time, and the propagating backward stop-and-go traffic jam appears. However, under the same sensitivity, the limit case ofτ=0.2, due to the stability condition is satisfied, the stop-and-go phenomenon disappears and traffic flow turns uniform over the whole space in Fig.4(d). The results demonstrate that the vehicle’s mechanical inertia effect has an important effect upon the property of traffic flow, which means that the stability effect is weakened gradually, and the stop-and-go traffic jam becomes more serious in the traffic system with the increase ofτ.

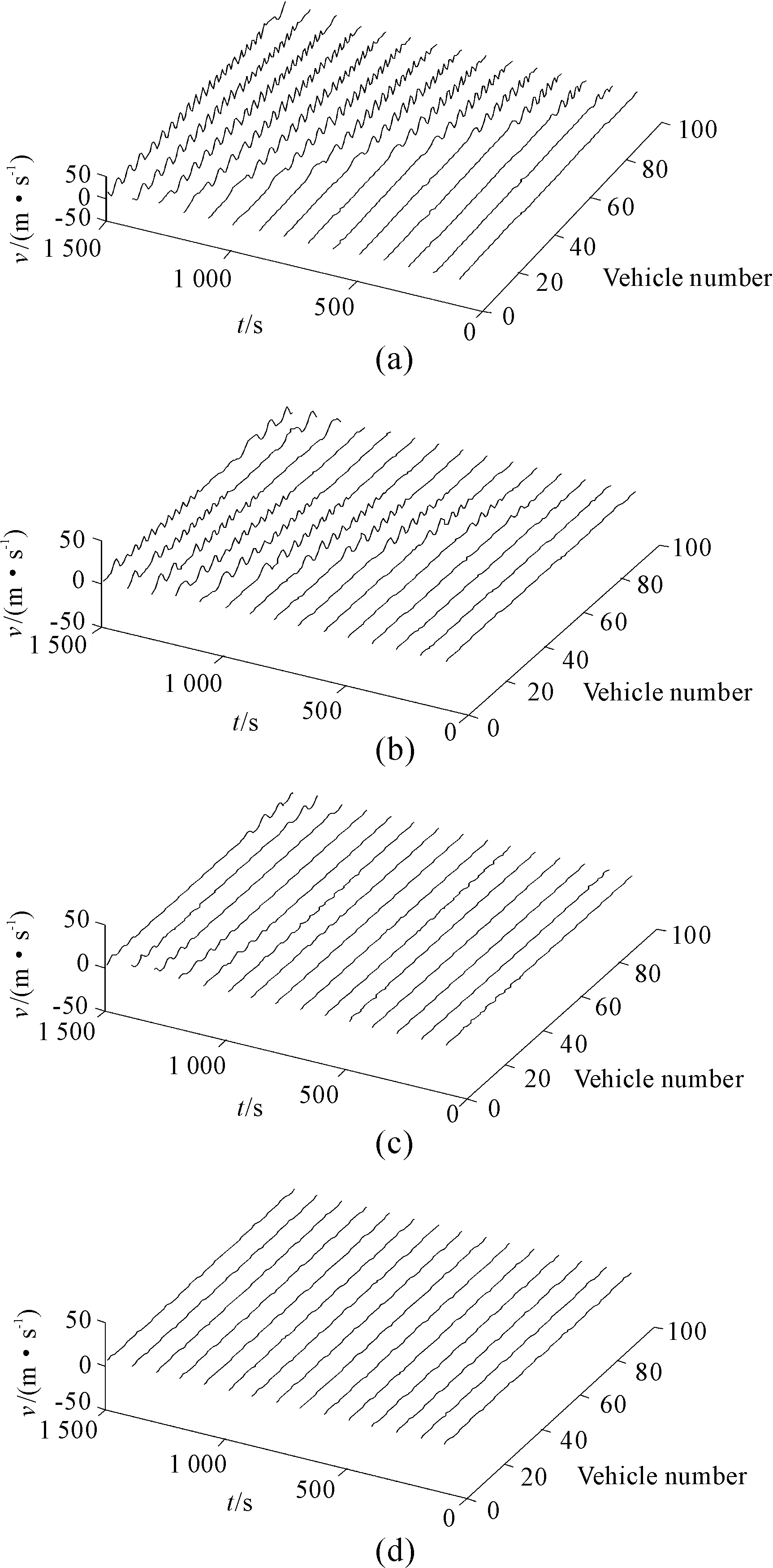
Fig.4 Space-time evolution of the headways aftert= 0 under the different value ofτ

5 Conclusions

In this paper, a new car following model is developed by taking the vehicle’s mechanical inertia effect into account on the basis of FVDM. The stability analyses have been conducted and the stable criterion is given by applying control theory. The comparisons between FVDM and our model are carried out in several simulations. The results of the starting up process show that the driving behaviors in our model are closer to the actual traffic phenomen. Finally the simulation of the vehicles’ dynamic evolution process indicates that the vehicle’s mechanical inertia has an important influence on the traffic flow.

Acknowledgements

This work was financially supported by Key scientific research project of the Chongqing Institute of Engineering (KJA201402), the Natural Science Foundation of China(61462008).

[1]Pipes L A.An operational analysis of traffic dynamics[J].Journal of Applied Physics, 1953, 24(3): 274-281.

[2]Chandler R E, Herman R, Montroll E W.Traffic dynamics: studies in car following[J].Operations Research, 1958, 6(2):165-184.

[3]Newell G F.Nonlinear effects in the dynamics of car following[J].Operations Research, 1961, 9(2):209-229.

[4]Gazis D C, Herman R, Rothery R W.Nonlinear follow-the-leader models of traffic flow[J].Operations Research, 1961, 9(4):545-567.

[5]Bando M, Hasebe K, Nakayama A, et al.Dynamical model of traffic congestion and numerical simulation[J].Physical Review E,1995, 51: 1035-1042.

[6]Helbing D, Tilch B.Generalized force model of traffic dynamics[J].Physical Review E, 1998, 58(1):133.

[7]Jiang R, Wu Q, Zhu Z.Full velocity difference model for a car-following theory[J].Physical Review E, 2001, 64(1):017101.

[8]Zhao X&Gao Z.A new car-following model: full velocity and acceleration difference model[J].The European Physical Journal B, 2005, 47(1):145-150.

[9]Ge H X, Cui Y, Cheng R J.A car-following model with considering control signals from front and rear[J].Acta Phys.Sin., 2014, 63: 110504-7.

[10]Yu S, Liu Q, Li X.Full velocity difference and acceleration model for a car-following theory[J].Communications in Nonlinear Science and Numerical Simulation, 2013, 18(5), 1229-1234.

[11]Tang T Q, Li C Y, Huang H J.A new car-following model with the consideration of the driver’s forecast effect[J].Phys.Lett.A, 2010, 374:1668-1672.

[12]Jin S, Wang D H, Tao P F, Li P F.Non-lane-based full velocity difference car following model[J].Physica A, 2010, 389:4654-4662.

[13]Zhou T, Sun D H, Kang Y R, Li H M,Tian C.A new car-following model with consideration of the prevision driving behavior[J].Commun.Nonlinear Sci.Numer.Simulat., 2014, 19:3820-3826.

[14]Zhou T, Sun D H, Li H M, et al.A new coupled map car-following model considering drivers’ steady desired speed[J].Chin.Phys.B, 2014, 23: 050203-5.

[15]Yu S, Liu Q, Li X.Full velocity difference and acceleration model for a car-following theory[J].Communications in Nonlinear Science and Numerical Simulation, 2013, 18: 1229-1234.

考慮車輛機械慣性效應的跟馳模型及其穩定性分析

周桐1,2*，陳渝光3，李雨宣1

1.重慶工程職業技術學院 信息工程學院, 重慶402260 2.重慶大學 計算機學院, 重慶400044 3.重慶理工大學 電子信息與自動化學院, 重慶400054

為了更加真實地描述在實際交通中的跟馳行為，基于全速度差模型，提出一個考慮車輛機械慣性的跟馳模型。應用線性控制理論給出模型的穩定性條件。與前人提出的模型仿真結果對比，理論結果與數值仿真一致，表明本文提出的模型能夠克服前人模型中靜止車隊啟動過程中頭車加速度出現瞬間跳躍現象，同時隨著車輛機械慣性系數的增加，交通擁堵更加容易發生。

交通流; 交通擁堵; 跟馳模型; 車輛機械慣性

9 March 2015; revised 7 June 2015;

Tong ZHOU, Lecturer, Post-doctor,

graduated from Chongqing University. E-mail: zhoutong

10.3969/j.issn.1001-3881.2015.18.024 Document code: A

U491.112

accepted 5 August 2015

851217@163.com

Hydromechatronics Engineering

http://jdy.qks.cqut.edu.cn

E-mail: jdygcyw@126.com