面向公差技術的幾何要素自由度表示與操作及其應用

吳玉光　劉玉生

1.杭州電子科技大學，杭州，3100182.浙江大學CAD&CG國家重點實驗室，杭州，310058

面向公差技術的幾何要素自由度表示與操作及其應用

吳玉光1劉玉生2

1.杭州電子科技大學，杭州，3100182.浙江大學CAD&CG國家重點實驗室，杭州，310058

描述了幾何要素的本征方向和本征自由度概念、幾何要素自由度的表示方法和約束自由度的計算規則。根據基本幾何元素的幾何特征以及與基準要素的位置關系確定了幾何要素的本征方向，根據幾何量測量原理，提出了基準要素約束自由度的計算方法，建立了基準體系約束自由度的計算規則。根據公差類型與基準要素和目標要素的關系，建立了公差設計正確性、完整性驗證的具體規則，提出了基于自由度分析的公差標注正確性驗證方法。

自由度；本征自由度；約束能力；公差驗證

0　引言

點、線、面是構成零件形體組成要素和導出要素的基本幾何元素，也是尺寸公差和幾何公差的標注對象和各類幾何檢驗工具的檢測目標。公差標準與規范的定義、公差分析與綜合的數學模型、公差標注正確性驗證等技術中均涉及幾何要素的自由度概念，基本幾何元素的自由度的表示與操作算法是公差分析和綜合的基礎技術。

基于自由度的公差分析和設計技術的研究[1-4]已取得了大量有價值的成果[5]。有關基準約束目標自由度的關系早就引起了人們的注意，吳永寬等[6]提出了基準約束目標自由度的具體條件，美國機械工程師協會報告ASME Y14.5.1[7]也在基準參考框架部分中討論了自由度概念，枚舉了點、線、面的全部相對位置關系，從幾何位置控制的角度得出只有6種類型的基準參考框架的結論，并列出了全部有意義的基準組合。Kramer[8]使用符號推理的方法來決定零件在裝配體內的自由度。Wu等[9]將自由度模型和屬性數據模型相結合來開發裝配公差模型。最近，Shen等[10]提出了確定一個基準體系自由度計算的代數公式，試圖將基準約束自由度能力的計算用于公差驗證技術中。

但現有的自由度分析方法對幾何要素自由度的認識還存在不足，未揭示自由度計算方法的規律，應用于公差分析和測量過程中還存在以下問題：①約束自由度計算公式沒有通用性，還不能處理被測目標與基準處于一般位置的情況；②不能指明約束給定自由度的具體基準，因此不能區分公差的各項組成指標與具體基準的關系，從而不能支持公差檢驗和公差標注正確性分析，造成當前CAD軟件的公差模塊均缺少公差標注合理性檢查功能;③現有自由度分析方法都假設基準框架體系內實際基準位于公稱位置，而忽視基準之間存在的相對位置誤差，造成公差帶的位置確定存在偏差，因而不利于保證公差設計、公差分析和公差分配方法的正確性。

本文研究基本幾何要素自由度的表示方法和基準約束自由度的計算方法，根據公差類型與自由度的關系建立公差標注的正確性檢查規則。

1　本征自由度與公差坐標系的定義

1.1基本幾何元素的本征方向和本征自由度的定義

幾何要素的本征方向為與幾何要素自身的幾何特性和它的基準相關的唯一的方向。對于直線目標，本征方向就是直線本身。對于平面目標，本征方向為目標平面的法線方向。而對于點目標要素，本征方向則根據不同的基準要素可分為以下幾種情況：基準點指向目標點的方向、經過目標點的基準直線的垂線方向、經過目標點的基準平面的法線方向。

相對于本征方向，各類公差對目標要素自由度的約束要求可以分為4 類：①約束本征方向的一個平移自由度；②約束垂直于本征方向的全部平移自由度；③約束本征方向的一個轉動自由度；④約束垂直于本征方向的全部轉動自由度。即幾何要素的自由度可以根據本征方向歸納為4類：線平移自由度、線轉動自由度、面平移自由度和面轉動自由度[11]，幾何要素自由度這一歸納分類已用于幾何要素控制點變動模型中[12]，本文將這4類自由度命名為本征自由度。點、線、面的傳統自由度和本征自由度定義如圖1所示。

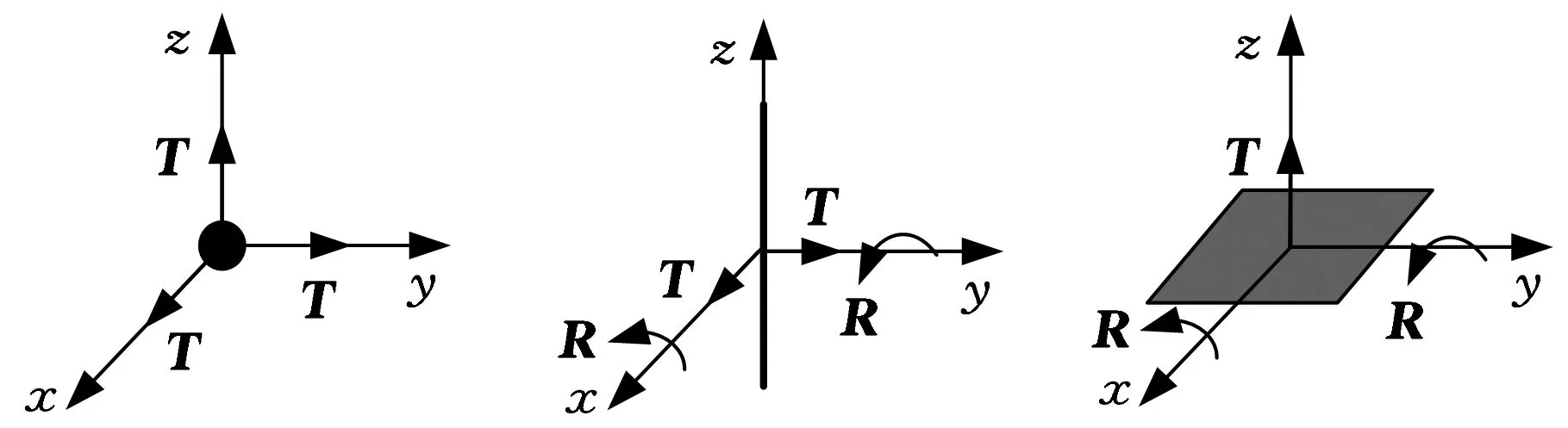
(a)點的傳統自由度　　　(b)直線的傳統自由度(c)平面的傳統自由度

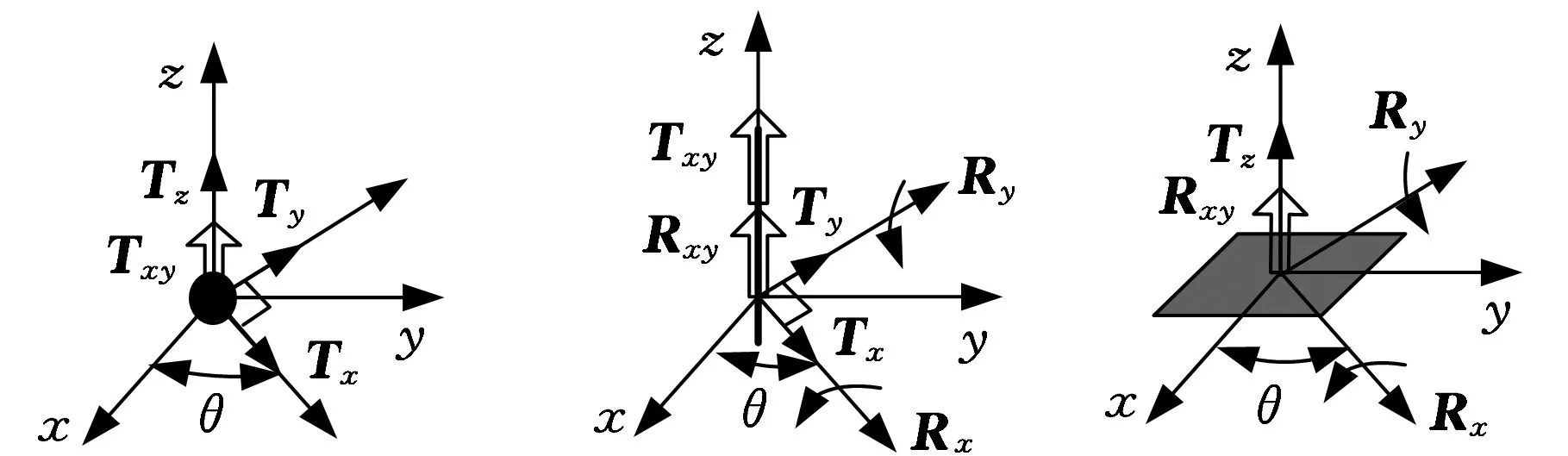
(d)點的本征自由度　　　(e)直線的本征自由度(f)平面的本征自由度圖1　自由度的定義

點、線、面等幾何要素的本征自由度可以概括為：①點具有1個線平移自由度和1個面平移自由度；②直線具有1個面平移自由度和1個面轉動自由度；③平面具有1個線平移自由度和1個面轉動自由度。本征自由度同樣也可以用單位矢量表示，如果將線平移自由度用單位矢量Tz表示，將面平移自由度用單位矢量Txy表示，則Txy可以分解為兩個垂直于本征方向的線平移自由度Tx、Ty，即Txy=Tx×Ty。同理，也可以將轉動自由度分別用單位矢量Rz、Rxy、Rx和Ry表示，其中Rxy=Rx×Ry。Txy、Rxy平行于本征方向，但由它們分解出來的Tx、Ty、Rx和Ry的方向是不確定的，確定方向還需要一個角度參數。可見這是本征自由度和傳統的自由度定義的差別，本征自由度的其他特性可參見文獻[12]。

1.2成組要素的本征自由度定義

由于成組要素是由點、線、面組成的一個整體幾何圖框，因此它具有與基本幾何要素不同的本征自由度。成組要素有圓形陣列和矩形陣列兩種布置方式。成組要素作為一個整體與外部基準建立公差關系，成組要素內部成員之間的公差屬于幾何要素之間的公差關系。無論是矩形陣列還是圓形陣列，其幾何圖框均可以用一對正交的矩形平面表示，對于圓形陣列，這對正交平面就是圓柱體的兩個正交的直徑平面；對于矩形陣列，正交平面就是空間立方體的兩個對稱面。定義幾何圖框的本征方向為兩個正交平面的交線方向，幾何圖框的自由度為兩個正交平面的本征自由度之和。因此，基準約束成組要素自由度的計算方法與約束兩個正交平面組合的自由度的計算方法相同。成組要素的本征自由度如圖2所示，除了沒有本征方向的1個移動自由度以外，成組要素具有5個自由度。

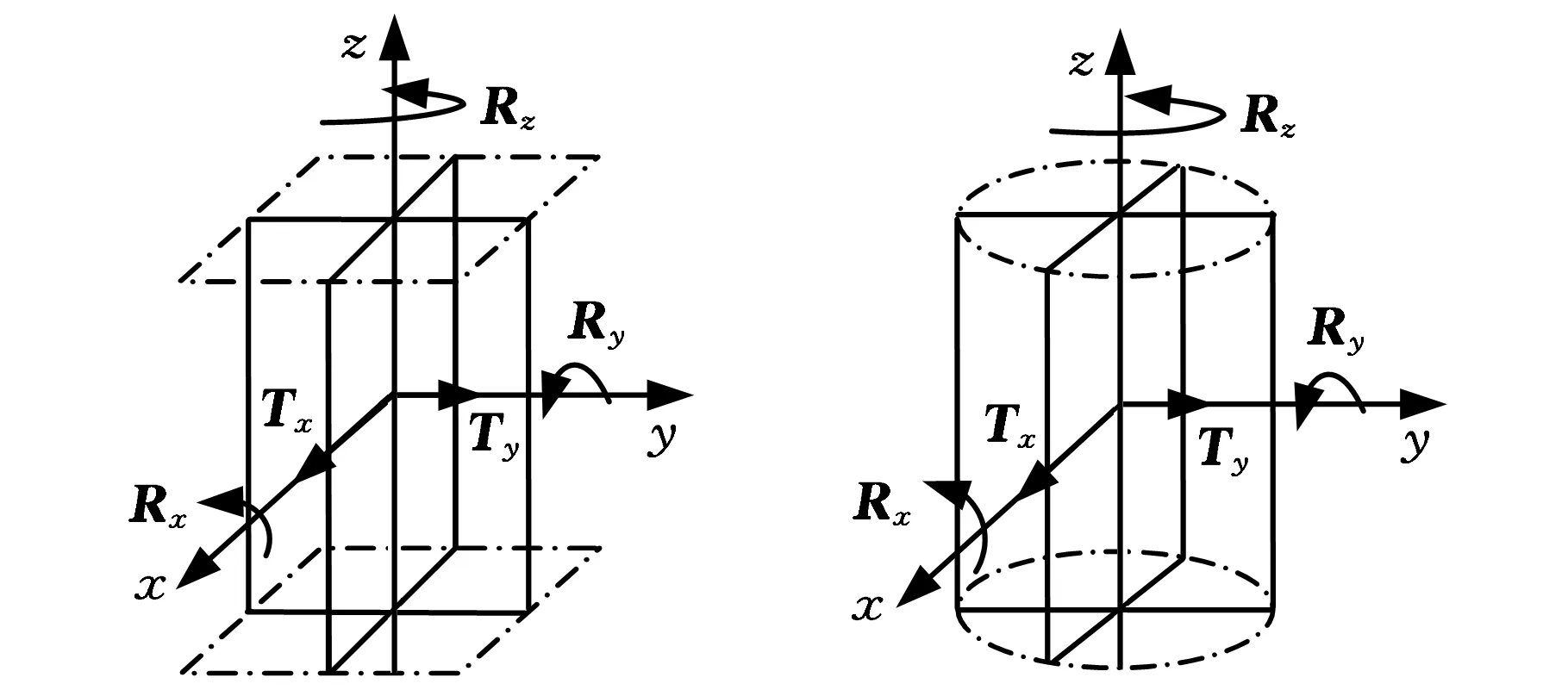
(a)矩形陣列(b)圓形陣列圖2　成組要素的本征自由度

1.3基于本征自由度的公差坐標系定義

公差坐標系用于定義幾何要素的變動和幾何要素公差帶的位置，公差坐標系建立在目標要素的公稱位置上，坐標系的原點為目標要素的中心，各坐標軸方向與本征方向和基準約束目標的自由度方向相關。定義本征方向可以為公差坐標系的一個坐標軸方向，如果Txy或Rxy能夠分解為Tx、Ty或Rx、Ry，則這兩個正交自由度方向就是公差坐標系的另外兩個坐標軸的方向。而能否分解以及是否有必要進行分解，則取決于公差的功能要求和基準的設置。因此，建立目標要素的公差坐標系的主要工作就是確定垂直于本征方向的線平移自由度或線轉動自由度。例如，圖2所示成組要素的公差坐標系的z軸方向為本征方向，x軸方向由被基準約束的線平移自由度Tx或線轉動自由度Rx的方向確定。

根據以上分析，公差坐標系坐標軸方向與基準約束目標自由度方向相同，可以同時確定，這種定義方式具有以下優點：

(1)根據公差類型和基準設置確定公差坐標系的類型，公差坐標系的類型包括圓柱坐標系、球面坐標系和直角坐標系等多種，不同的公差類型需要建立不同類型的公差坐標系；

(2)基準要素控制目標要素變動方向與公差坐標系的坐標軸、坐標平面相同，便于公差的驗證和測量；

(3)目標要素的位置變動在公差坐標系上定義，便于公差分析過程中模擬幾何要素變動。

2　基準對目標自由度約束能力的計算

2.1基本幾何元素約束自由度的原理

基準能夠約束目標要素的自由度就是可以確定目標要素相對于基準的距離和角度，因此通過分析目標要素相對于基準要素的距離和角度參數定義的完備程度，就可以獲得基準約束目標自由度的程度。為此，提出距離測量方向線和角度測量平面兩個概念。

距離測量方向線(DMDL)定義：點、線、面基準要素和目標要素之間的距離測量方向線必須是兩者之間的最短距離直線或兩者之間的公垂線。

角度測量平面(AMP)定義：直線、平面基準要素和目標要素之間的角度測量平面是以三個矢量之一為法線的平面，三個矢量為兩條直線矢量的矢量積、直線矢量與平面法線的矢量積、兩個平面法線的矢量積。

根據以上概念，基準約束目標自由度的機理可以利用距離和角度測量原理來解釋，目標要素某一方向的平移和轉動自由度被基準約束，本質上是指目標要素相對于基準在該方向的距離和角

度能夠測量并且唯一。因此，基準能夠約束目標的平移自由度表明基準和目標兩者之間存在DMDL，基準能夠約束目標的轉動自由度表明基準和目標兩者之間存在AMP。判斷基準能否約束目標自由度就是找出基準和目標兩者之間的獨立的DMDL和獨立的AMP，而基準約束自由度的程度則可以通過基準和目標兩者之間具有的獨立的DMDL和獨立的AMP的數量來衡量。

2.2幾何要素之間的DMDL和AMP的確定方法

分析點、線、面之間所有可能的相對位置情況可知，基準要素與目標要素兩者之間存在的DMDL是以下6種直線之一：①直線與直線的公垂線；②直線與平面的公垂線；③平面與平面之間的公垂線；④經過點的直線的垂線；⑤經過點的平面的垂線；⑥兩點的連線。基準要素與目標要素兩者之間的AMP是以下4種平面之一：①兩共面直線所在平面；②以兩直線的公垂線為法線的平面；③同時平行于直線和平面法線的平面；④同時平行于兩個平面法線的平面。因此，對于約束平移自由度的判斷，可以查找以上6個DMDL的存在情況，對于約束轉動自由度判斷，可以查找4個AMP的存在情況。由于目標要素的理想位置是確定的，因此只要確定DMDL和AMP法線的方向，就確定了被基準所約束的自由度的方向。為了敘述方便，將6個DMDL單位方向矢量分別用符號D1、D2、…、D6表示，將4個AMP的單位法線用A1、A2、A3、A4表示。

當基準與目標要素處于一些特殊位置時，如點-點、點-線、線-線重合以及線-面垂直、面-面平行等，這些情況下均具有兩個DMDL和AMP，它們的具體方向不確定但均垂直于目標要素的本征方向，仿照本征自由度的定義，將這種特定的DMDL和AMP法線用平行于本征方向的單位矢量表示，并分別命名為Dxy、Axy。顯然Dxy=Dx×Dy，Axy=Ax×Ay，其中，Dx、Dy就是兩個方位確定而方向未定的DMDL的方向矢量，Ax、Ay就是兩個AMP單位法線矢量。幾何元素之間的DMDL和AMP如表1所示，其中成組要素的DMDL和AMP用兩個正交的平面進行計算。根據本征自由度概念，Dxy和Axy與目標要素的面垂直自由度矢量方向相同，如果基準要素與目標要素之間存在的Dxy或Axy全部不能分解為Dx、Dy或Ax、Ay，則目標要素的面垂直自由度不能分解為線垂直自由度。

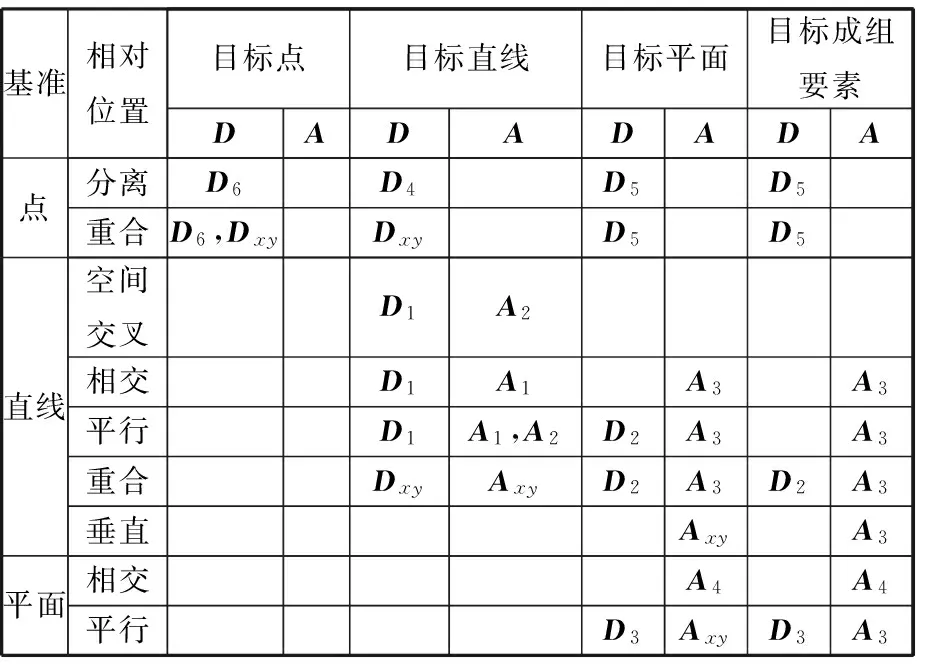
表1　幾何元素之間的DMDL和AMP

2.3基于DMDL和AMP的公差坐標系的建立規則

根據基準約束目標本征自由度的原理，公差坐標系定義如下：①公差坐標系的原點與目標幾何要素的中心重合，即點、線、面幾何要素的坐標原點分別為點本身、直線的中點、平面的包圍盒的中心；②公差坐標系的z軸為幾何要素的本征方向；③公差坐標系的x軸方向為基準約束目標自由度的方向，y軸方向根據右手法則確定。設目標要素的本征方向為Dp，根據基準順序和基準與目標之間的距離測量方向線Di(i=1,2,…,6)和角度測量平面法線確定Aj(j=1,2,3,4)，則通過判斷基準體系中的全部基準的Di和Aj與Dp位置關系，就可以確定公差坐標系的x軸方向：

(1)如果存在Di并且Di⊥Dp，或者如果存在Aj并且Aj⊥Dp，則Di(或Aj)就是公差坐標系的x軸方向；

(2)如果存在Dxy或Axy，則垂直于本征方向的任意方向都可以作為x軸方向，這種情況適用于對基準約束目標的垂直自由度的方向沒有要求的公差。

3　基準體系的約束自由度能力計算

3.1單一基準約束自由度的能力判斷方法

單一基準約束自由度的能力取決于基準與目標之間的DMDL和AMP數量，根據DMDL方向和AMP法線與目標要素的本征方向的關系，即可確定自由度約束情況。對于給定的基準和目標要素，首先確定目標要素的本征方向Dp、本征自由度Tz、Txy和Rz、Rxy，然后計算兩者之間的Di、Dxy和Aj、Axy，最后對每一個本征自由度建立相應的判斷規則。對于平移自由度，約束自由度判斷規則包括：①Tz能夠被約束的條件是存在Di并且Tz與Di不垂直；②Txy能夠被約束的條件是存在Dxy并且Dxy=Txy；③Txy能夠分解的條件是存在Di且Txy不平行于 Di，此時規定Tx被約束，未約束的自由度Ty可以根據公式Txy=Tx×Ty求得；④Tx能夠被約束的條件是存在Dxy并且Dxy垂直于Tx，或存在Di并且Tx不垂直于Di。表2所示為平移自由度的約束判斷規則，由于Txy方向不確定，約束分兩種情況：①全部約束但方向不確定；②分解成兩個線垂直自由度Tx、Ty并且只約束Tx。

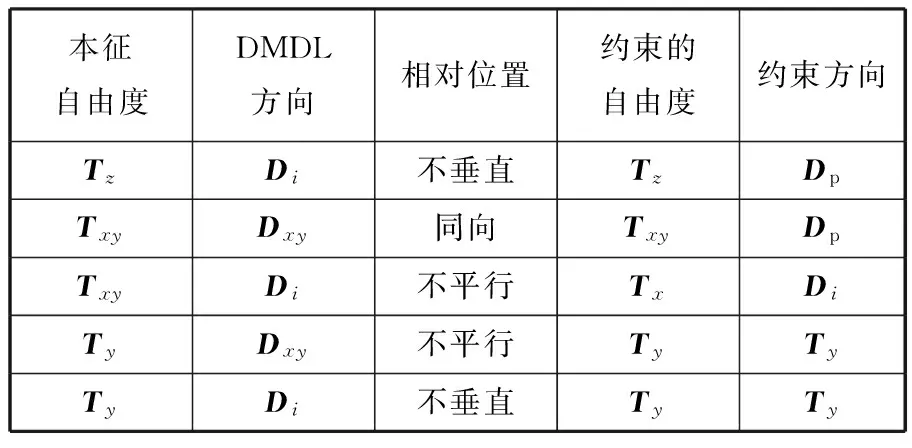
表2　本征自由度的計算規則

約束轉動自由度的判斷規則與約束平移自由度完全相同，只要把表2中的T、D分別用R、A替換即可。

3.2基準組合約束自由度能力計算方法

基準組合與組合基準不同，基準組合是指基準體系中的兩個或三個基準可以組合而形成一個新的幾何類型，如兩個點基準組合等效于一個直線基準、兩條平行直線組合等效于一個平面基準。除了第一成員基準的約束自由度能力以外，通過基準組合而得到的新幾何類型具有組合成員單獨存在時所不具有的約束自由度能力，如兩個平行的圓柱同時作為一個目標要素的基準時，雖然其中一個圓柱屬于基準冗余，但兩個圓柱會組成一個平面基準，從而使兩個圓柱基準組合還具有平面基準的約束自由度能力，因而增加了對目標自由度的約束。由于公差的基準數量最多只有三個，因此進行組合的基準數量只有兩個基準的組合和三個基準的組合兩種情況。

兩個基本幾何元素的組合又可以分為點-點、點-線、點-面、線-線、線-面、面-面6種，其中只有點-點、點-線、線-線三種組合可以形成新的幾何類型，即分別等效于直線、平面、平面，如圖3a、圖3b、圖3c所示。三個不同類型的幾何要素雖然可以產生非常多的組合，但能產生新的等效幾何類型的組合有兩種情況：①第一、第二、第三基準的幾何類型均為點；②第一、第二基準的幾何類型均為點、第三基準的幾何類型為平行于前兩點連線的直線。即前兩個基準均為點時可組合成線，再與第三個點基準或平行直線基準組合成面，如圖3d、圖3e所示。可行的基準組合必須具備能夠產生新的幾何類型和增加約束自由度能力兩個條件，只有圖3所示的幾何類型和相對位置下才可能組合形成能增加約束能力的新的幾何類型。

(a)點-點　(b)點-線　　(c)線-線　　　(d)點-點-點(e)點-點-線圖3　基準組合

計算基準組合的約束自由度能力時，首先計算當前基準單獨作用時的約束自由度能力，然后計算當前基準與高序基準組合產生的新幾何類型的約束自由度能力，由基準組合而增加的約束自由度由參與組合的基準共同承擔，該自由度所對應的公差分量以參與組合的基準的等效幾何類型作為測量基準，該自由度的方向也由等效幾何確定。

3.3基準體系約束自由度能力的計算

以往的研究中首先確定基準體系整體的約束自由度能力，再根據目標要素相對于基準體系的位置計算目標的自由度約束情況。這種方法不能判斷每一個基準具體的約束自由度情況，也沒有考慮基準組合的作用，無法確定每一個基準的設置合理性，因此不適合公差標注的驗證方法。本文方法認為基準體系約束自由度的能力為基準單獨約束自由度的能力和基準組合約束自由度的能力之和，基準體系約束自由度的計算就是建立被約束的本征自由度的集合，該集合包括約束的本征自由度和承擔該約束任務的基準與基準組合。根據幾何要素本征自由度的定義和表2的約束自由度計算方法，并且遵循基準優先原則，容易建立這一關聯關系。利用關聯關系可以為基準設置正確性判斷、公差檢測規劃制定等應用提供依據。

4　基于本征自由度的公差標注正確性驗證

4.1公差標注正確性驗證規則

公差標注的正確性主要體現在公差類型選擇的有效性、各種公差之間關系的一致性、公差數值設置的合理性、自由度約束的完整性以及公差原則設置的合理性等多個方面[13-14]，這些方面的檢查方法都涉及幾何要素的自由度約束問題，如根據基準體系的約束自由度能力計算可以發現欠公差、過公差問題以及不適當的基準設置，根據目標的自由度約束情況可以判斷公差數值設置的合理性、公差關系的一致性等。因此，約束自由度計算方法是公差標注的正確性驗證的主要工具，根據約束自由度計算可以找出不正確的尺寸與公差標注，從而使公差設計和標注軟件具有自校正功能。

公差標注正確性檢查必須基于實體模型和三維公差標注，首先需要建立公差與基準關系的數據結構，該數據結構存儲了基本幾何元素和成組要素的每一個幾何公差和尺寸公差的公差類型、公差數值及修飾符、根據優先關系排列的各基準以及應用的公差原則。然后確定目標幾何要素的本征方向，確定目標要素的本征自由度Tz、Rz、Txy、Rxy。最后對每一個公差標注逐個判斷基準設置的合理性、基準設置的充分性、公差設置的冗余性，這樣可以保證每一步檢測到錯誤就可以針對性地給出出錯信息。利用基準約束自由度能力計算方法可以建立公差標注的有效性檢查規則，具體規則如下。

(1)基準體系約束能力檢查規則：每一個公差的基準體系至少必須能夠約束表3中該公差項目的一個自由度，否則基準體系的約束能力不足。當公差值帶有修飾符Φ時，基準體系必須約束表3中該公差項目的垂直自由度(Txy和Rxy)，否則基準體系的約束能力不足。

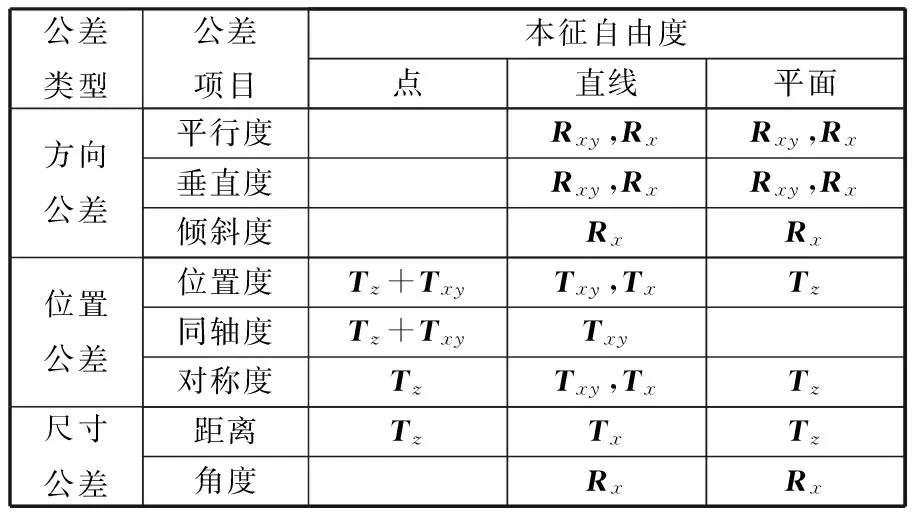
表3　各類公差需要約束的自由度

(2)冗余基準檢查規則：根據表3公差類型與幾何要素約束自由度的關系，確定幾何要素必須約束的自由度。根據基準優先原則，逐個對基準進行判斷，如果當前基準及其與高序基準的組合不能約束目標要素剩余未約束自由度，則當前基準為冗余基準。

(3)冗余公差檢查規則：如果幾何要素的當前公差所必須約束的自由度已全部被其他公差所約束，則當前公差為冗余公差。可以為每一個幾何要素設置一個本征自由度表，根據表2的計算方法為每一個自由度指定承擔約束任務的基準，建立約束自由度信息關聯關系表，則公差是否冗余就可以通過檢索自由度約束關聯關系表進行判斷。

(4)方向公差可應用性檢查規則：方向公差控制目標要素的轉動自由度，如果被測要素不存在需要約束的轉動自由度(Rz、Rxy、Rx、Ry)，則方向公差不可應用。

(5)位置公差可應用性檢查規則：位置公差控制目標要素的平移自由度，如果被測要素不存在需要約束的平移自由度(Tz、Txy、Tx、Ty)，則位置公差不可應用。

(6)尺寸公差標注的正確性檢查規則：如果目標的一個轉動自由度被約束，則該轉動自由度方向的夾角只能標注理想角度尺寸。如果目標的一個平移自由度被約束，則該平移自由度方向的距離只能標注理想距離尺寸。

(7)修飾符使用合理性檢查規則：只有點和直線目標要素的公差值可以帶有修飾符Φ。當基準體系只能約束直線目標的垂直平移自由度Txy和約束垂直轉動自由度Rxy時，位置公差和方向公差的公差值必須帶有修飾符Φ；當目標和基準要素均為點并且兩者重合時，位置公差的公差值必須帶有修飾符sΦ。

(8)公差標注的完整性規則：通過基準體系的約束能力計算可以發現目標要素沒有約束的自由度，從而發現遺漏標注的距離尺寸和角度尺寸，同時也提醒設計者是否存在遺漏的公差標注。

(9)復合公差標注時公差體系的細化原則：當存在位置公差和方向公差復合情況時，位置公差的基準約束本征自由度必須包含方向公差的約束自由度，并且方向公差值必須小于位置公差值，否則不符合公差細化原則。當存在兩種方向公差復合時，高層公差框格的基準所約束的有效自由度必須超過低層公差框格的基準所約束的有效自由度，即高層公差必須存在不同于低層的另一方向的有效約束，同時低層的公差值必須小于高層公差值，否則，低層方向公差屬于冗余公差。

4.2公差標注的正確性驗證實例

圖4為一法蘭盤的公差標注情況，其中的目標要素C和D的幾何公差基準存在順序設置錯誤，運用本文的公差標注的正確性驗證規則分析如下。

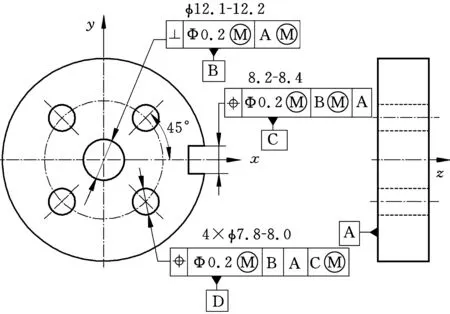
圖4　幾何公差標注的正確性驗證

目標C的自由度約束情況：第一基準B具有約束目標要素的自由度Tz和Rxy中Rx的能力，第二基準A不能約束目標要素的另一個線垂直自由度(該自由度繞z軸轉動)，基準A和基準B沒有組合的可能，因此判斷結果基準A為冗余基準。雖然位置度公差為綜合公差，方向公差的缺省值等于位置公差，故從約束自由度的角度看，Rxy沒有必要約束，但設計意圖可能要求目標C關于基準A和基準B的垂直度同等重要，因此如果系統提示基準A冗余，此時會提醒設計者注意查找出錯原因。此外，由于目標要素的幾何類型為平面，因此目標C的公差值帶有修飾符Φ也是冗余的。

目標D的自由度約束情況：目標D為成組要素，其自由度為Rz、Tx、Ty、Rx、Ry。第一基準B約束了一個目標的4個線平移自由度Tx、Ty、Rx和Ry，第二基準A沒有約束剩余的自由度，第二基準A與第一基準B沒有組合形成新的幾何類型的可能，此時得出1個出錯信息，即基準A為冗余基準。第三基準C約束目標D的線平行轉動自由度Rz。其他規則檢驗也沒有發現違背情況，該公差標注具有一個出錯信息。如果設計意圖需要保證成組要素的4個孔與底面垂直，則必須把基準目標A作為第一基準，從而約束了目標D的兩個線垂直面轉動自由度Rx和Ry，然后保證目標D的中心與基準B的同軸度，約束目標D的兩個線垂直面平移自由度Tx和Ty，最后約束目標D繞自身軸線的轉動角度，因此目標D的位置度公差的合理基準順序為基準A、基準B和基準C。

5　結論

(1)描述了幾何要素的本征方向概念和本征自由度的定義，保證約束自由度的計算方法具有一般性，且便于進行裝配公差分析和公差技術與CAD實體模型集成。

(2)基于本征自由度，分析了幾何要素約束自由度的原理，給出了幾何要素約束目標自由度能力的計算方法，可方便快捷地計算出被測目標被基準約束的具體自由度。

(3)提出了基于距離測量方向線和角度測量平面概念的幾何元素約束自由度計算原理，建立了單一基準和基準組合約束自由度能力的計算方法。

(4)提出了基于本征自由度的公差標注正確性和完整性驗證的啟發性規則。

[1]Zhang B C. Geometric Modeling of Dimensioning and Tolerancing[D]. Tempe: Arizona State University, 1992.

[2]Wu Y. Development of Mathematical Tools for Modeling Geometric Dimensioning and Tolerancing[D] . Tempe: Arizona State University, 2002.

[3]Shah J J, Yan Y, Zhang B. Dimension and Tolerance Modeling and Transformations in Feature Based Design and Manufacturing[J]. Journal of Intelligent Manufacturing, 1998, 9(5):475-488.

[4]Kandikjian T, Shah J J, Davidson J K. A Mechanism for Validating Dimensioning & Tolerancing Schemes in CAD Systems[J]. Computer Aided Design, 1999, 33(10):721-737.

[5]Ameta G, Serge S, Giordano M. Comparison of Spatial Math Models for Tolerance Analysis: Tolerance-maps, Deviation Domain and TTRS[J]. Journal of Computing and Information Science in Engineering， 2011, 11: 021004-1-021004-8.

[6]吳永寬，于連璋. 零件與工裝的形位精度理論與應用[M].北京：機械工業出版社，1994.

[7]ASME. Mathematical Definition of Dimensioning and Tolerancing Principles[S]. New York :American Society of Mechanical Engineers, 1994.

[8]Kramer G A. Solving Geometric Constraint Systems: A Case Study in Kinematics[M]. Cambridge, Massachusetts: MIT Press, 1992.

[9]Wu Y, Shah J J, Davidson J K. Computer Modeling of Geometric Variations in Mechanical Parts and Assemblies[J]. Journal of Computer and Information Science in Engineering,2003,3(1):54-63.

[10]Shen Y, Shah J J, Davidson J K. Feature Cluster Algebra in Geometric Dimensioning and Tolerancing[C]//Proceedings of the ASME IDETC/CIE. Washington D C, 2011: 709-722.

[11]吳玉光. 基于工序要求的夾具定位方案自動規劃方法[J].機械工程學報，2010, 46(11):185-192.

Wu Yuguang. Approach to Automated Location Planning for Fixture Based on the Processing Procedure Requirements[J]．Journal of Mechanical Engineering，2010，46(1 11：185-192．

[12]吳玉光, 張根源. 基于幾何要素控制點變動的公差數學模型[J]. 機械工程學報, 2013, 49(5):138-146.

Wu Yuguang, Zhang Genyuan.Tolerance Mathematical Model Based on the Variation of Control Points of Geometric Element[J]. Journal of Mechanical engineering, 2013, 49(5): 138-146.

[13]Shen Z S. Tolerance Analysis with EDS/VisVSA[J]. Journal of Computing and Information Science in Engineering, 2003, 3:95-99.

[14]劉玉生,曹衍龍. TolRM：面向三維CAD的公差建模系統[J]. 計算機輔助設計與圖形學學報, 2006, 18(8):1179-1184.

Liu Yusheng，Cao Yanlong. TolRM: a 3D CAD Oriented Tolerance Modeling System[J]．Journal of Compuler-Aided Design & Computer Graphics, 2006，18(8)：1179-1184．

(編輯袁興玲)

DOF Representation and Operation of Geometric Feature and Its Applications for Tolerance Technology

Wu Yuguang1Liu Yusheng2

1.Hangzhou Dianzi University,Hangzhou,310018 2.The State Key Lab of CAD&CG,Zhejiang University,Hangzhou,310058

The intrinsic direction of geometric feature, the representation method and calculation rules of DOF of geometric feature were proposed. The intrinsic direction of geometric feature was determined based on the geometric characteristics and position relations among toleranced geometry feature and datum geometry feature. According to the geometric measurement principles, the computation method of constraint capability of datum feature to the DOF of target feature was proposed,and the calculation rules of constrained DOF of toleranced features were proposed by datum reference frames. The tolerance specification validation method were proposed according to the relationship among tolerance type and geometry of the datum and target entity , and the correctness and completeness validation rules were discussed against the dimensioning and tolerancing standards and against good practice rules in industries.

degree of freedom (DOF); intrinsic DOF; constraint capability; tolerance verification

2014-07-10

國家自然科學基金資助項目(51175132,61173126)

TP39.72DOI：10.3969/j.issn.1004-132X.2015.11.014

吳玉光，男，1961年生。杭州電子科技大學機械工程學院教授、博士。研究方向為夾具自動設計、公差技術等。發表論文60余篇。劉玉生，男，1971年生。浙江大學CAD&CG國家重點實驗室教授、博士。