多梳櫛經編機成圈運動及其機構分析與設計
沈惠平 李 密 王敏其 王 水 尹洪波 左雙雙
1.常州大學,常州,213016 2.常州市武進五洋紡織機械有限公司,常州,213164
多梳櫛經編機成圈運動及其機構分析與設計
沈惠平1李密1王敏其2王水2尹洪波1左雙雙1
1.常州大學,常州,2130162.常州市武進五洋紡織機械有限公司,常州,213164
在吸收、掌握國外經編機機構設計精髓的基礎上,對多梳櫛經編機的成圈運動及其機構實現進行了深入研究。首先,介紹了成圈機構、成圈過程及其工作原理,設計出具有停歇功能的斯蒂芬森六桿傳動機構,并通過共享一個不同相位角的三拐曲軸,將三個六桿傳動機構與3-DOF平面八桿成圈子機構串接,設計出單主軸驅動的3-DOF平面22桿經編成圈主機構,并進行機構運動學分析;然后,根據梳櫛上導紗針的排布以及成圈工藝,規劃成圈運動軌跡的關鍵特征點,并用最小二乘法擬合出各運動軌跡的多項式函數;最后,對3-DOF平面22桿經編成圈主機構進行整體建模分析,并運用遺傳算法對其進行了基于成圈運動軌跡逼近的機構參數優化設計。
經編機;平面連桿機構;停歇機構;軌跡綜合;遺傳算法
0 引言
經編針織物與緯編針織物相比,具有生產效率高、延伸性比較小、脫散性好、適應于不同粗細紗線以及幾乎所有織物組織等優點,因此,其應用領域已從傳統的服裝和裝飾領域擴大到了工業、農業、建筑、交通、國防、航空航天以及醫療衛生等產業領域,如產業用經編針織物包括篩網、漁網、傳送帶、降落傘、育秧網、護林網、帳篷、紗布、人造血管等[1]。
國外經編機產業發展迅速,其中,德國卡爾邁耶公司目前的世界市場占有率在85%以上。按工作原理分,經編機分為特里科型和拉舍爾型兩大類, 其高效生產的關鍵是成圈主機構的設計與制造,成圈主機構設計復雜,制造和安裝精度要求也很高。目前,國內經編機的機械結構大多仿制卡爾邁耶公司的產品,盡管已有山東、江蘇、福建等多個地區生產銷售各種經編機,且國內已有學者進行分析研究, 但迅速適應新經編工藝及其織物結構的機構設計原理,以及高速化機器的動平衡等關鍵技術仍沒有掌握[2]。因此,學習消化國外經編機技術,掌握實現經編成圈運動機構的拓撲結構、運動學、動力學設計的理論與方法,對改進現有的或設計具有知識產權結構或技術的經編機,具有重要的現實意義和應用前景。
拉舍爾經編機根據配置的梳櫛數不同,分為多梳櫛和少梳櫛,少梳櫛經編機由于具有梳櫛少、整個梳櫛搖架質量輕、體積小等特點,所以可使梳櫛搖架擺動故橫移運動以實現墊紗。對于少梳櫛經編機的成圈運動,文獻[3-4]對成圈機件運動的相互協調與配合進行了研究,并給出了相應的停歇機構;文獻[5]給出了經編機成圈機構運動曲線及其機構實現的計算方法和電算程序。
多梳櫛經編機由于梳櫛數較多,整個梳櫛搖架的整體質量和體積太大,搖架不再擺動,致使成圈過程的各個運動均要由質量較輕的槽針、針芯塊、脫圈板等構件實現[1-2],因此,機構設計更加復雜,目前,對于多梳櫛經編機成圈運動和成圈機構的系統研究相對較少[6]。
本文對多梳櫛經編機的成圈運動及其機構實現進行了深入的研究和創新設計。
1 多梳櫛經編機的成圈運動及機構實現
1.1成圈子機構及其組成
成圈子機構是指握持或驅動槽針、針芯塊和脫圈柵狀板(簡稱脫圈板)等促使紗線彎曲成線圈串套編織的機構。如圖1所示,該機構運動的成圈構件分別是脫圈板1、槽針2和針芯塊3,易知,R1-P1-R2-R3-R4構成兩自由度平面五桿機構,然后在含槽針2的構件上串接一個Ⅱ級桿組P2-R5-R6,從而形成3-DOF平面八桿成圈子機構。從圖1并結合圖2可以看到,脫圈板1繞一固定軸R1作純擺動,其頂點a的軌跡應為一條近似于直線的圓弧段Ⅰ*(圖2中的點線),而作平面運動的槽針2的頂點b的軌跡曲線Ⅱ*(圖2中的細實線),及針芯塊3的頂點c的軌跡曲線Ⅲ*(圖2中的虛線)均為復雜的平面一般曲線。合理控制三個輸入角θ00、θ10和θ20,可使三個輸出構件1、2、3產生相對運動,實現如圖2所示的主要成圈運動軌跡(Ⅰ*、Ⅱ*、Ⅲ*)。
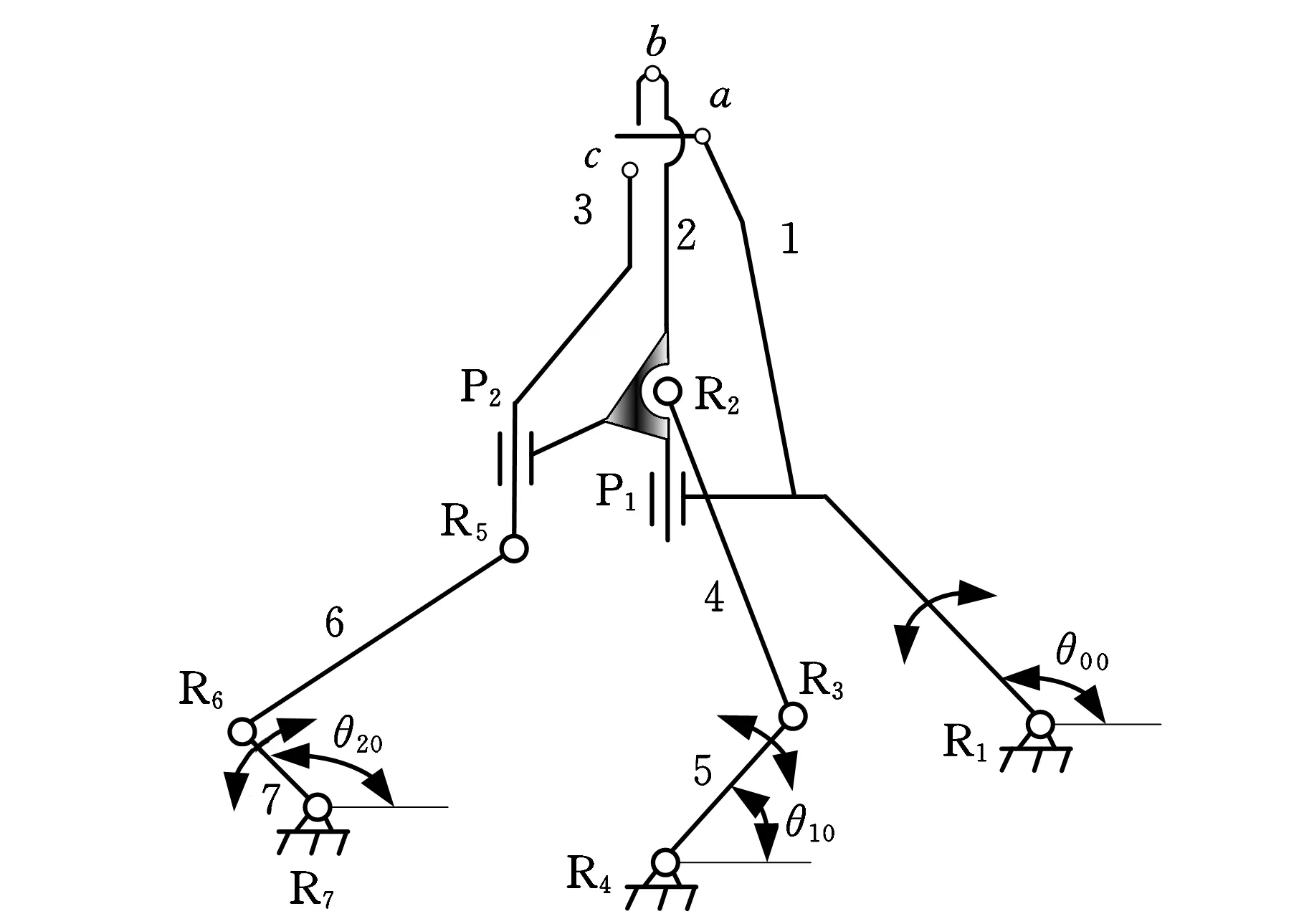
圖1 成圈子機構簡圖

圖2 多梳櫛經編機成圈運動軌跡圖
1.2成圈運動的工作原理
圖2所示為拉舍爾經編機梳櫛排列示意及成圈軌跡。導紗針8固定于梳櫛,其橫移運動由電子橫移機構實現(垂直于紙面,未畫出)。
多梳櫛經編機成圈運動過程及其工作原理如下:
(1)槽針2從①處開始(此時,脫圈板1擺至最左端近乎停歇靜止),相對于脫圈板1快速上升,同時,藏于槽針2內的針芯塊3處于較慢上升狀態,槽針2口中的線圈由拉力作用退到槽針槽壁上。
(2)當槽針2頂點b運動到相對脫圈板1頂點a16 mm左右的②處時,退圈運動完成。此時,相關梳櫛要求完成橫移,準備好針背墊紗,脫圈板1開始向右擺動,針芯塊3保持藏于針槽狀態,槽針背依次打過導紗針中的紗線至右端③處,實現針背墊紗。脫圈板1在最右端附近有近似停歇(移動緩慢),等待④處右側導紗針橫移運動完成,脫圈板1開始向左回擺進行針前墊紗。
(3)在④處附近脫圈板1近似停歇后繼續向左回擺,同時槽針2相對脫圈板1開始快速下降,針芯3相對脫圈板1慢速下降,針芯3逐漸刺出槽針壁(此時槽針壁外的紗線應被壓住以防止被刺出的針芯塊3封于槽針口內)并封住槽針口內的紗線,針芯塊3封住槽針口后同槽針2保持相對靜止一起下降至⑤處。
(4)槽針2頂點b下降至相對脫圈板1頂點a下端1 mm左右處時,脫圈板1已脫去槽針壁外的舊線圈,槽針口中紗線形成新線圈,針芯塊3相對槽針2繼續下降,槽針口打開。
(5)槽針2繼續運動至⑥處附近,舊線圈被拉出后,脫圈板1擺回到最左端,槽針2相對脫圈板1快速上升,針芯塊3慢速上升保持藏于槽針壁內,運動到①處時一個成圈周期運動完成。
1.3傳動子機構
上述3-DOF平面八桿成圈子機構的三個輸入角是由傳動子機構實現的。目前,傳動機構大多數采用凸輪機構,其優點是易實現復雜成圈運動軌跡,設計簡單,但加工困難,高速時噪聲大;連桿機構的設計要求較高,但加工容易,且易實現高速低噪,因此,經編機傳動機構的發展趨勢是越來越多地使用連桿機構,包括最簡單的四連桿機構或基于瓦特鏈和斯蒂芬森鏈的六桿機構,也有采用八桿機構或以上的多桿機構[7]。
由于斯蒂芬森六桿機構具有良好的停歇性能[8],因此,本文設計基于斯蒂芬森鏈的傳動機構,如圖3所示,其中,桿A0A為曲柄,桿D0D為輸出構件,輸出量可以是位移或轉角。按機構停歇性質,其輸出的位移或轉角函數有三種:①在一極限位置近似停歇;②在途中一位置近似停歇;③在兩極限位置近似停歇[7,9]。本文采用前兩種停歇形式,如圖3a、圖3b所示,圖3c、圖3d所示分別是兩種停歇的輸出函數形式。
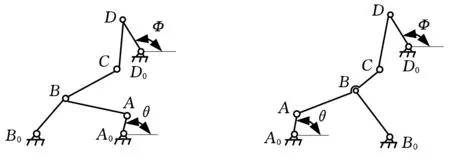
(a)一極限位置停歇(b)途中一位置近似停歇
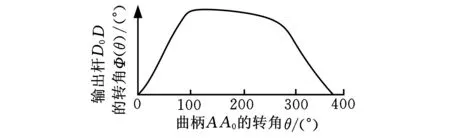
(c)圖a機構的輸出
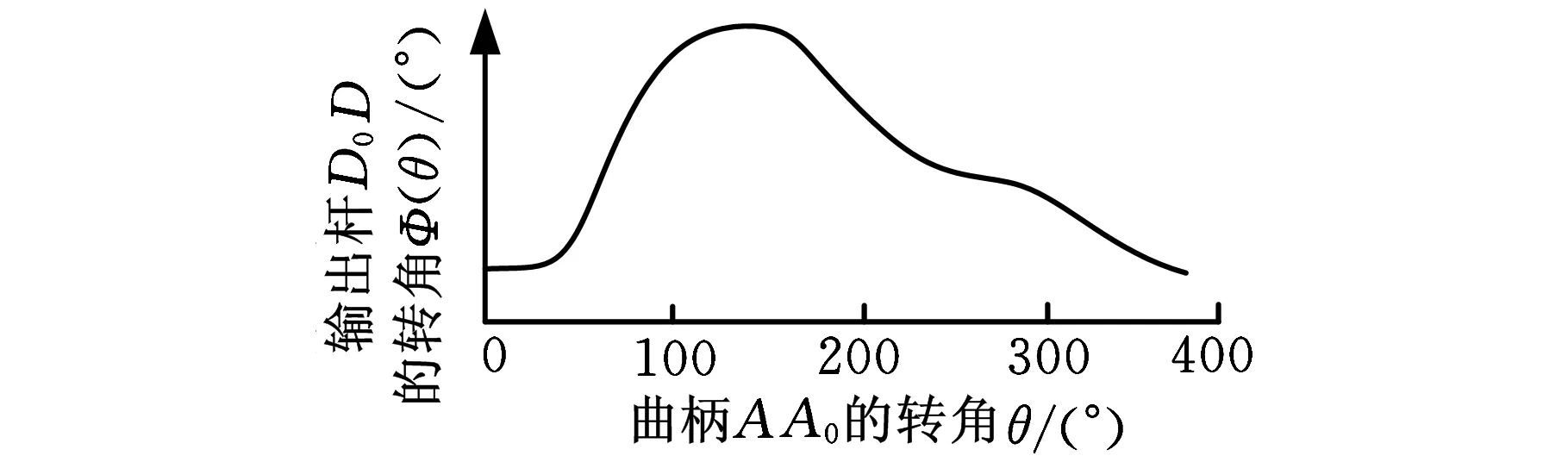
(d)圖b機構的輸出圖3 六桿傳動機構及其兩種停歇形式
1.4經編機成圈主機構的設計
將圖3所示六桿傳動機構的輸出構件D0D,分別與圖1所示成圈子機構的三個輸入構件1、5、7固接,即設計出圖4所示的經編機成圈主機構,其中,R10、R20、R30位于同一單主軸上,但其曲柄相位角不同。顯然,這是一個3-DOF平面22桿Ⅱ級機構,它可視作由左、中、右三條支鏈構成,其中,中、右兩條支鏈構成一個2-DOF的平面15桿Ⅱ級機構。
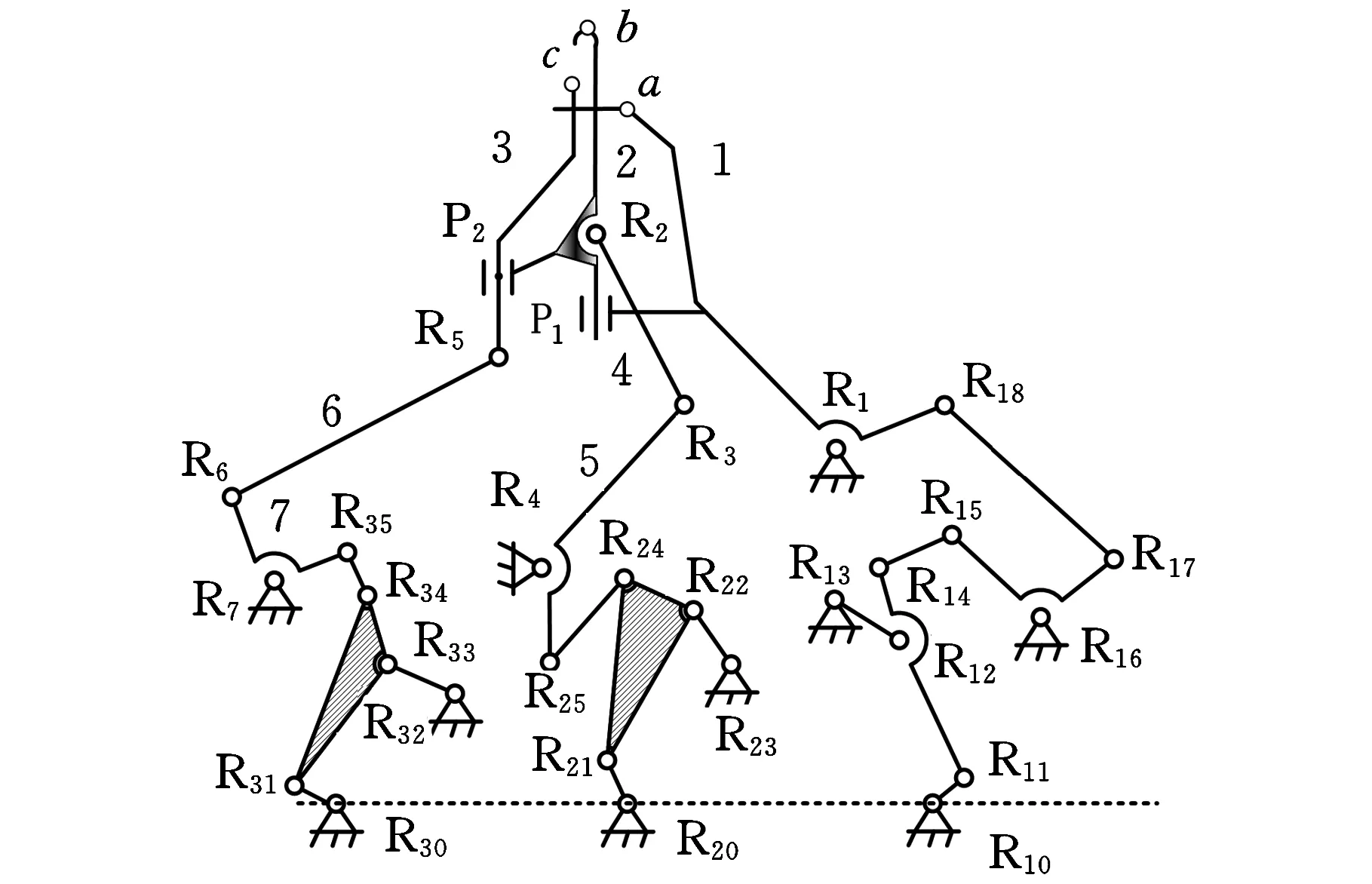
圖4 經編機成圈主機構簡圖
2 機構運動學分析
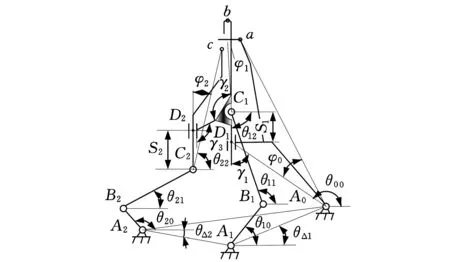
圖5 3-DOF平面八桿成圈子機構簡圖
2.1機構位置正解
機構的位置正解為已知輸入量θ00、θ10和θ20,求輸出量a、b和c三個點的坐標。
(1)回路A1-B1-C1-D1-A0的位置向量方程為
LA1B1ej θ10+LB1C1ej θ11+S1ej θ12=
LA1A0ej θΔ1+LA0D1ej θ00
(1)
按實部和虛部展開、化簡,并消去S1解得
A=A0+B0B=2C0
C=A0-B0
A0=sinθ12(LA1A0cosθΔ1+LA0D1cosθ00)+
cosθ12LA1B1sinθ10-cosθ12(LA1A0sinθΔ1+
LA0D1sinθ00)-sinθ12LA1B1cosθ10
B0=LB1C1sinθ12
C0=LB1C1cosθ12
從而有
S1=(LA1A0sinθΔ1+LA0D1sinθ00-LA1B1sinθ10-
LB1C1sinθ11)/sinθ12其中,θ12=θ00-γ1,θΔ1為機架已知夾角。
(2)回路A1-B1-C1-D2-C2-B2-A2的位置向量方程為
LA2B2ej θ20+LB2C2ej θ21+S2ej θ22=
LA2A1ej θΔ2+LA1B1ej θ10+LB1C1ej θ11+LC1D2ej θ13
(2)
其中,θ22=θ12+π/2-γ3,θ13=θ12+γ2,θΔ2為機架已知夾角。同樣,展開、化簡并消去S2解得
教師主導式的意思是指教師策劃與主導及引導學生每一步之學習,例如,教師講解;準備一系列問題引導學生思考,學習不同種類的音樂;準備好實驗程序,讓學生跟著步驟進行實驗。
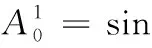
LB1C1cosθ11+LC1D2cosθ13)+cosθ22LA2B2sinθ20-
cosθ22(LA2A1sinθΔ2+LA1B1sinθ10+
LB1C1sinθ11+LC1D2sinθ13)-sinθ22LA2B2cosθ20
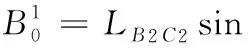
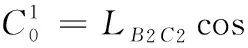
進一步,求得:
S2=(LA2A1sinθΔ2+LA1B1sinθ10+LB1C1sinθ11+
LC1D2sinθ13-LA2B2sinθ20+LB2C2sinθ21)/sinθ12
至此,輸出a、b和c三點的位置可表示為
a=A0+LA0aej(θ00-φ0)
(3)
b=A1+A1B1+B1C1+LC1bej(θ12+φ1)
(4)
c=A2+A2B2+B2C2+LC2cej(θ22-φ2)
(5)
2.2機構位置逆解
機構的位置逆解為已知輸出量a、b和c三個點的坐標,求輸入量θ00、θ10和θ20。
(1)由式(3),求得
(6)
(2)由
b=A0+LA0D1ej θ00+S1ej θ12+LC1bej (θ12+φ1)
求得
S1=(Reb-ReA0-LA0D1cosθ00-
LC1bcos(θ12+φ1))/cosθ12cosθ12≠0
(3)由
C1=A0+LA0D1ejθ00+s1ejθ12=
A1+LA1B1ejθ10+LB1C1ejθ11
按實部和虛部展開、化簡并消去θ11,可求得θ10:
(7)
B=-4n
m=ReC1-ReA1
n=ImC1-ImA1
(4)同理,可以求得第三個輸入角θ20,由
C2+LC2cej(θ22-φ2)=c
A2+LA2B2ejθ20+LB2C2ejθ21=C2
可求得θ20:
(8)
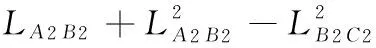
B=-4n
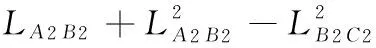
m=ReC1-ReA2
n=ImC2-ImA2
基于式(6)~式(8),可方便地獲得成圈運動軌跡與三個輸入角之間的關系;同時,筆者已對位置正逆解公式進行了數值互算,驗證了其正確性。
用同樣的方法,可建立傳動子機構的位置正逆解析解;進一步,機構各點的線速度、加速度以及所有桿件的角加速度量也易求得,在此從略。
3 成圈工藝軌跡規劃
3.1成圈軌跡特征點的規劃
經編機成圈運動的復雜程度取決于梳櫛數目及編織工藝。圖6為排布好的梳櫛組件及其上的導紗針的平面視圖,導紗針排布和織花工藝決定了成圈構件所需完成的運動,其中,在曲線Ⅱ*上選取槽針2頂點b軌跡的一系列關鍵點,其形成的軌跡路徑要依次劃過導紗針8的針孔中心附近,到達右端后折回,然后下降。
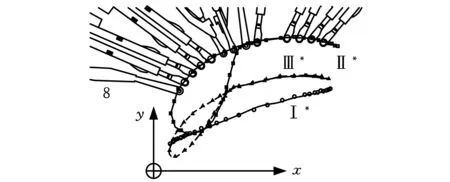
圖6 成圈軌跡關鍵點
由于脫圈板1、針芯塊3都與槽針2有相對位置關系,因此,軌跡Ⅰ*、Ⅲ*的關鍵特征點也可規劃確定。取經編機主軸中心為原點建立平面直角坐標系,特征點選取時要注意曲線的平滑性,槽針2特征點數據如表1所示。
3.2曲線擬合及數據點采樣
根據以上導紗針的排布,取值點數量有限且規劃出的成圈軌跡點過于粗糙。為獲得平面連桿機構更易實現的軌跡,需根據特征點擬合出平滑曲線函數,并據此重新離散,取出有利于后續設計的軌跡特征點。
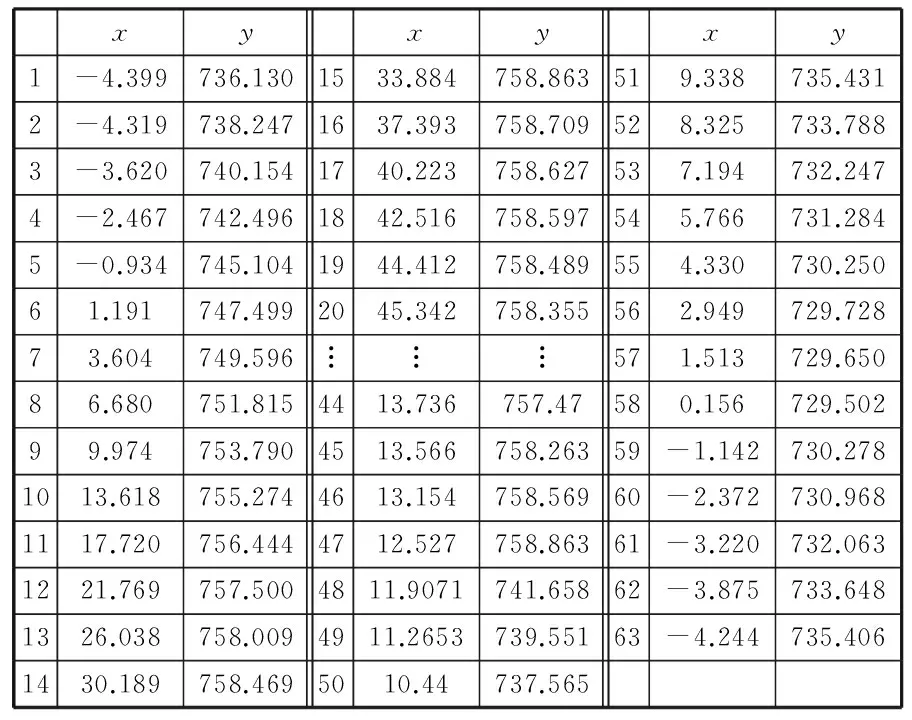
表1 槽針數據點 mm
3.2.1曲線擬合
(1)脫圈板1的軌跡為標準圓弧段,其函數容易獲得,設脫圈板擺動中心R1坐標為(u,v),擺動半徑為R,則有軌跡函數:
(9)
(2)槽針2和針芯塊3的軌跡為一般平面曲線,為更好地擬合出光滑曲線函數,先分別把槽針2和針芯塊3特征軌跡曲線點分為三段,再進行多項式函數擬合,如圖7所示。例如槽針2的曲線分為:曲線段1(a1→b1)、曲線段2(b1→c1)及曲線段3(c1→a1)。其中,分割點a1、b1分別取在軌跡線最左、最右端,這樣,曲線段1(a1→b1)類似一個簡單圓弧;分割點c1取軌跡線的開合處,形成近似圓弧段2(b1→c1)及近似拋物線段3(c1→a1)。
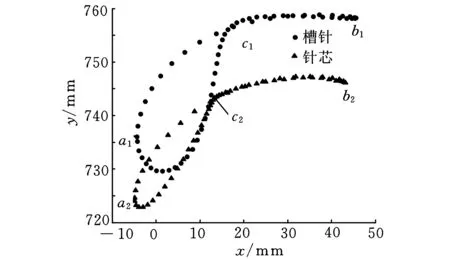
圖7 成圈軌跡的劃分
于是,槽針2頂部b點軌跡的三段函數為
同樣,針芯塊3頂點c點軌跡的曲線段1(a2→b2)、曲線段2(b2→c2)和曲線段3(c2→a2)的三段函數為
取多項式函數:
為求解此曲線擬合問題[10],記偏差為
(10)
令
則有δ2(c1,c2,…,cn)=‖Ac-b‖2
由多元函數極值的必要條件知,式(10)的最小偏差的解滿足:
因此可由最小二乘法擬合出相應的各段函數,槽針2頂點b的軌跡函數為
(11)
針芯塊3頂點c的軌跡函數為
(12)
由于槽針軌跡與針芯塊軌跡類似,這里只給出槽針2軌跡函數的擬合效果,如圖8所示。圖中圓點為曲線段1、2、3的規劃特征點;線條為擬合出的軌跡函數曲線。
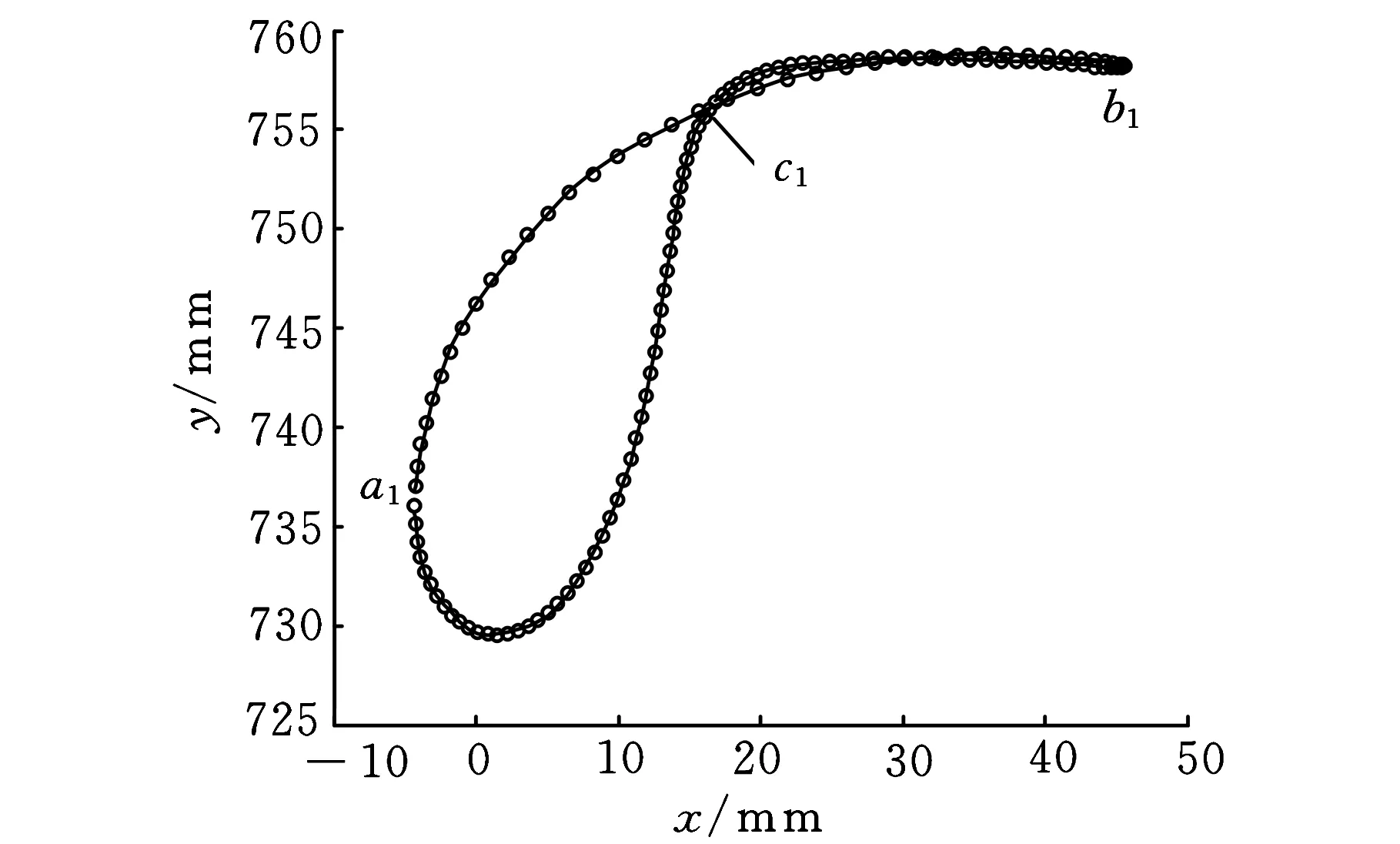
圖8 槽針2軌跡函數擬合效果
3.2.2數據重新采樣
運用式(9)、式(11)、式(12),可方便地獲得脫圈板1、槽針2和針芯塊3各頂點軌跡的任意精確數據點。由圖1可知:
(13)
其中,(x1,y1)、(x2,y2)、(x3,y3)分別為脫圈板1、槽針2和針芯塊3頂點的坐標。
由1.4節可知,經編機一般采用機械式高可靠性與穩定性的單主軸驅動作為傳動輸入,因此,需要合理規劃單主軸轉角θ和成圈機構輸入角(θ00、θ10和θ20)之間的映射關系。
由圖1可知,成圈子機構可看作由三條“支鏈”構成:右側“支鏈”中的脫圈板1為剛體定點擺動,容易規劃出它與單主軸驅動轉角θ的對應映射關系;而另外兩條“支鏈”在此單主軸上的相位角,與轉角θ分別存在相位差Δφ1和Δφ2,即
(14)
根據式(13)、式(14),以及成圈子機構的位置逆解(式(6) 、式(7) 、式(8)),即可得出主軸轉角θ與脫圈板1、槽針2和針芯塊3輸出軌跡點對應的數據。主軸轉角θ和槽針2頂點b軌跡之間的對應關系如表2所示(脫圈板1、針芯塊3的軌跡數據略)。
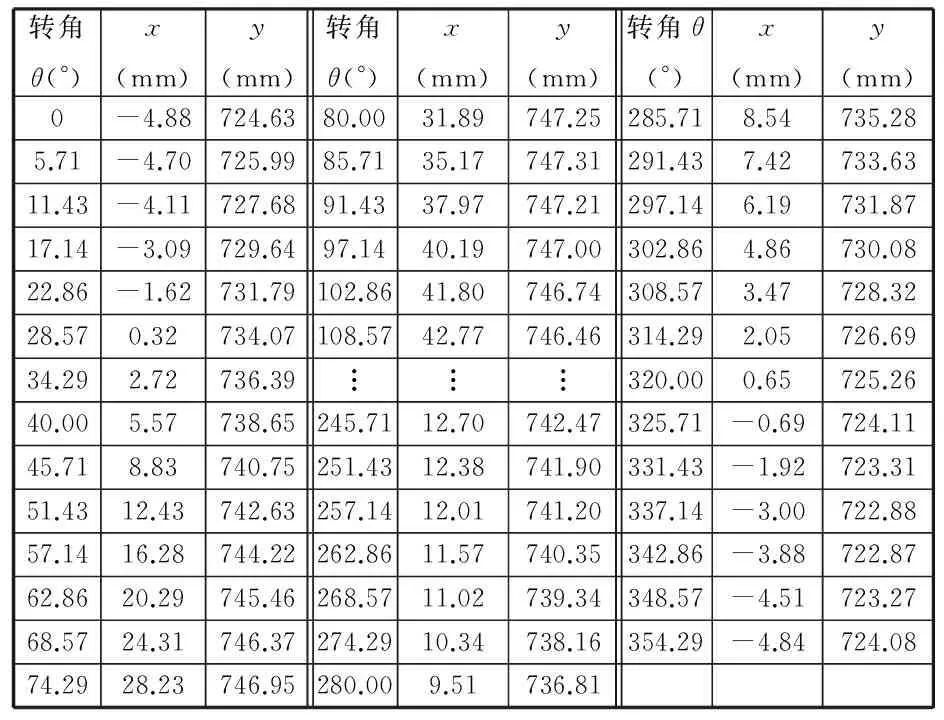
表2 主軸轉角θ與槽針2頂點b的軌跡的對應關系
4 經編機成圈主機構的建模與優化
4.1確定設計變量
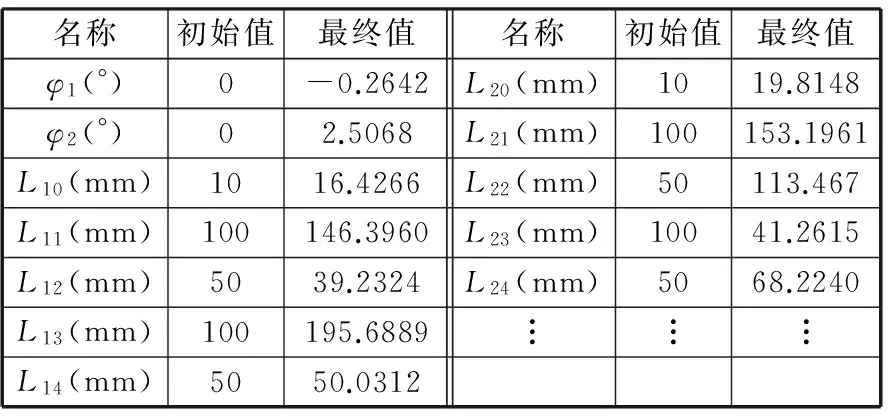
本文以圖4所示機構中的一部分2-DOF平面15桿Ⅱ級機構為例進行優化設計。如圖9所示,轉動副R10,R13,R16,R1,R20,R23,R4的軸孔坐標為已知值,這里,共取22個設計變量,即初始角φ1和兩個曲柄相位差φ2、桿長變量Li j,(i=1,2;j=0,1,2,…,9),即
X=[X1X2…X22]T=
[φ1φ2L10L11…L19L20L21…L29]T
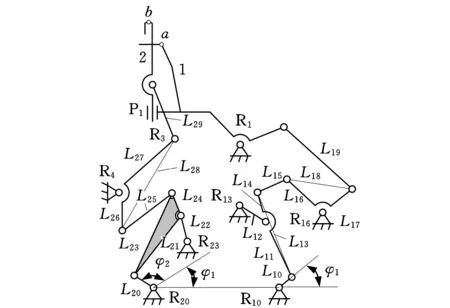
圖9 子機構軌跡優化設計模型
4.2建立目標函數
由1.2節成圈運動分析已得到理論軌跡,故只需進行軌跡重現即可。由于機構受油箱空間約束,因此,引入桿長約束:
lijmin 同時,需要對機構引入曲柄存在條件以及曲柄搖桿機構的最小傳動角為45°兩個約束。 于是,建立如下目標函數: (15) 圖10 經過6000代后的成圈軌跡擬合結果 在成圈子機構和傳動子機構位置逆解的基礎上,本文基于遺傳算法[11]設計了可視優化程序。根據經驗給定初始值及搜索范圍,初始種群大小為500,設置停止迭代誤差10-5,經過6000代進化,得到如圖10所示的優化結果,表3給出了部分變量的初始值及優化后的最終數值,其中,Ⅰ、Ⅰ*分別為脫圈板a點的實際軌跡曲線和理論軌跡曲線;Ⅱ、Ⅱ*分別為槽針b點的實際軌跡曲線和理論軌跡曲線。顯然,實際軌跡已高度逼近理論軌跡,其累積誤差的平方和僅為33.46,計算數據點為2×720組(0~360°,每0.5°取-值),平均誤差值僅為0.0232,因此,其22個優化值可作為圖9所示機構構型的全局最優尺寸。 表3 部分設計變量及其優化值 基于上述設計理論和方法,自主設計了單主軸驅動的多梳櫛經編機,其三維CAD模型如圖11所示。目前該機型(圖12)已投入小批量生產,各項性能指標達到設計要求。 圖11 主機構三維CAD圖圖12 多梳櫛經編機(局部) (1)理解、吸收國外機構設計的精髓,對提高我國包括經編機等在內的新型紡織裝備的自主創新設計能力具有重要意義,值得借鑒的經驗是: ①傳統意義上,一般認為移動副有較大滑動摩擦力,不宜作為被動運動副出現在平面多桿機構中,尤其在高速情況下,但本文所述的3-DOF八桿成圈子機構的實際情況并不如此,共出現了2個被動移動副P1與P2(兩自由度平面五桿機構R1-P1-R2-R3-R4內的移動副P1,以及連桿(槽針2)上的移動副P2),且實際情況運行得很好。這是因為,一方面,機構在工作運動過程中,移動副受力方向與速度方向一致,正壓力引起的摩擦力很小;另一方面,動程很小(h=20mm),即使使用移動副,也無妨大礙;再者,由于采用了專業的高精度直線軸承,保證了實際效果。 ②3-DOF八桿成圈子機構同時有三個輸出構件1、2、3的輸出點參與了工作,即其三個輸出點的軌跡有序協調完成了復雜的成圈運動;且其三個傳動機構通過共享一個三曲拐主動軸的傳動方式,實現了整個經編系統的高度集成化,保證了機器的較小體積,這也是較為突出的設計特點。 (2)本文對多梳櫛拉舍爾經編機成圈主機構進行了系統分析、計算及設計,獲得了設計的關鍵技術與方法,主要創新工作有: ①根據梳櫛上導紗針的排布以及成圈工藝,規劃出了成圈運動軌跡的關鍵特征點,并采用最小二乘法擬合出各自運動軌跡的多項式函數。 ②將三套斯蒂芬森六桿傳動機構與3-DOF平面八桿成圈子機構的輸入構件固接,設計成單主軸驅動的平面3-DOF 22桿經編機主機構。 ③建立了平面3-DOF 22桿經編機主機構(包括平面八桿成圈子機構、六桿傳動子機構)的運動學模型,在此基礎上運用遺傳算法對經編機主機構進行了參數優化設計。 (3)建立了單主軸驅動的多梳櫛經編機成圈系統的結構學、運動學設計方法,進一步有待建立其動力學及其動平衡設計理論和方法,為適應今后的產品自主改型設計與優化奠定理論基礎。 [1]蔣高明,顧璐英.國內外經編技術最新進展[J].針織技術,2010(1):1-3. Jiang Gaoming,Gu Luying.The Latest Progress of the Domestic and Foreign Warp Knitting Technology[J].Knitting Technology,2010(1):1-3. [2]蔣高明.經編裝備技術研究研究現狀和發展趨勢[J].紡織學報,2012,33(12):140-144. Jiang Gaoming.Present Research Situation and Developing Tendency of Warp Knitting Equipment and Technology[J].Journal of Textile Research,2012,33(12):140-144. [3]曹清林.經編機梳櫛擺動機構的運動設計[J].針織技術,2013,1(2):60-64.Cao Qinglin.On Designing the Movement of the Guide Bar Swinging Mechanism on a Warp-knitting Machine[J].Knitting Technology,2013,1(2):60-64.[4]馮怡,邱正明.高速槽針經編機成圈機構的研究[J].華東紡織工業學院學報,1984,10(4):29-37. Feng Yi,Qiu Zhengming.Studies on the Stitching Mechanism of High Speed Slider Neddle Knitter[J].Journal of East China Institute of Textile Science and Technology,1984,10(4):29-37.[5]南孝榮.自動繪制經編機成圈運動曲線程序設計[J].天津紡織工學院學報,1989,20(1):90-95. Nan Xiaorong.Program Design for Knitting Motion Curve Automatic Drawing of Warp Knitting Machine[J].Journal of Tianjin Institute of Textile Science and Technology,1989,20(1):90-95. [6]曹清林,王小霞.多梳經編機復合針運動機構的設計[J].江蘇技術師范學報,2011,4(4):1-9. Cao Qinglin,Wang Xiaoxia.Design on the Compound Needle Mechanism of the Warp Knitting Machines[J].Journal of Jiangsu Teachers University of Technology,2011,4(4):1-9. [7]伏爾默 J,洛克 K,伊默,等.連桿機構[M].石澤昌,陸錫年,陳立周,譯.北京:機械工業出版社,1989. [8]劉軍,李團結.平面多桿停歇機構優化設計研究[D].西安:西安電子科技大學,2007. [9]華大年,華志宏.連桿機構設計與應用創新[M].北京:機械工業出版社,2008. [10]徐明華,張燕新,李志林.數值分析[M].北京:高等教育出版社,2012. [11]王小平,曹立明.遺傳算法理論、應用與軟件實現[M].西安:西安交通大學出版社,2002. (編輯袁興玲) Knitting Motion Analysis and Mechanism Design for Multi-bar Warp Knitting Machine Shen Huiping1Li Mi1Wang Minqi2Wang Shui2Yin Hongbo1Zuo Shuangshuang1 1.Changzhou University,Changzhou,Jiangsu,213016 2.ChangzhouCity Wujin Wuyang Textile Machinery Co., Ltd.,Changzhou,Jiangsu,213164 On the basis of understanding basic principles for mechanism design of foreign warp knitting machines,knitting motion and the mechanism for performing the motion were studied systematically.Firstly,knitting mechanism,knitting processes and its working principles were introduced and Stephenson 6-link transmission mechanism with intermittent function was designed.By sharing a three-thrown crank shaft,three 6-link transmission mechanisms and 3-DOF plane 8-link knitting sub-mechanism were concatenated.A 3-DOF plane 22-link knitting main mechanism with single driving axis was designed and its kinematics property was also analyzed.Secondly,the key feature points of knitting action were planned based on the configuration of guide needles and knitting processes and the polynomial function of each trajectory was obtained by least square method.Further,the whole physical model of the 3-DOF plane 22-link knitting main mechanism was analyzed and optimum design of mechanism parameters was conducted based on the knitting action trajectory approaching using genetic algorithm. warp knitting machine;plane linkage;intermittent mechanism;trajectory synthesis;genetic algorithm 2014-03-19 江蘇省科技成果轉化專項資金資助項目(BA2013030);國家自然科學基金資助項目(51375062) TH11DOI:10.3969/j.issn.1004-132X.2015.11.007 沈惠平,男,1965年生。常州大學機械工程學院教授、博士研究生導師。主要研究方向為機構學、并聯機構。獲發明專利41項,發表論文130余篇。李密,男,1989年生。常州大學機械工程學院碩士研究生。王敏其,男,1963年生。常州市武進五洋紡織機械有限公司高級工程師。王水,男,1988年生。常州市武進五洋紡織機械有限公司工程師。尹洪波,男,1989年生。常州大學機械工程學院碩士研究生。左雙雙,男,1989年生。常州大學機械工程學院碩士研究生。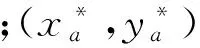
5 經編機成圈主機構的樣機研制

6 結論

