輪履復合救援機器人的乘適性分析與優化

李　浩　侍才洪　康少華　張西正

1.天津理工大學，天津，300384　　2.軍事交通學院，天津，300161 3.軍事醫學科學院，天津，300161

輪履復合救援機器人的乘適性分析與優化

李浩1,3侍才洪3康少華2張西正3

1.天津理工大學，天津，3003842.軍事交通學院，天津，300161 3.軍事醫學科學院，天津，300161

研究了一種新型輪履復合式救援機器人，它可通過輪履結構的轉換在災難現場等復雜環境中高效地解救和運送傷員。出于對解救傷員在運送過程中安全性、舒適性的考慮，對救援機器人以輪式狀態運送傷員的過程進行了振動分析，并利用ADAMS建立救援機器人輪式結構的動力學模型，對其在實際路況的運行進行了仿真分析。考慮人體不同部位不同方向具有不同的頻率加權，利用MATLAB設計相應濾波器對仿真所得振動曲線進行處理以計算救援機器人的乘適性。以獲取更好的乘適性為目標，通過MATLAB優化工具箱對救援機器人懸架參數進行了優化設計，并進一步驗證了優化結果的合理性。

輪履復合；動力學分析；乘適性；優化設計

0　引言

近年來國內外對救援機器人的研究開發日益重視，并已取得顯著成就[1]。目前的救援機器人不僅能夠探測發現傷者，還具有轉運傷員的功能，比較典型的有日本救援機器人RoboCue。本文研究的救援機器人是一種應用于災難現場救援的機器人，具有搜救并轉送傷員的功能。由于救援機器人的工作環境通常為復雜多變、不可預測的非結構環境，故為了提高救援效率，救援機器人采用輪履復合式結構[2]。

救援機器人解救的多為骨折、燒傷、大量出血等傷勢較重的傷員，不能再對其產生二次傷害，否則會給傷員帶來更大的疼痛，并使傷情惡化，甚至危及生命。因此，救援機器人在轉運傷員的過程中必須考慮乘適性[3]。輪履復合式救援機器人有輪式和履帶式兩種工作狀態，可根據不同路況要求快速地進行輪履結構間的轉換。通常輪式相對于履帶式有較高的行進速度、較好的平穩性，可用于快速轉運傷員，但在實際轉送傷員過程中，救援機器人結構特殊性等因素會對其乘坐舒適性產生影響，需要加以分析計算。

本文研究的是一種新型輪履復合式救援機器人，目前國內外相關的研究和報道相對較少。本文將車輛行駛動力學的相關理論和救援機器人的自身結構相結合，對救援機器人輪式狀態高速運行的乘適性進行分析并做出相應的優化。

1　救援機器人結構簡介

本文研究的救援機器人沿用一款全地形車(ATV)的懸架系統，前后均為獨立懸架。與一般輪履復合式結構不同，救援機器人行走系統采用輪履復合變體輪，四輪獨立驅動。配備有超聲波傳感器、紅外傳感器等輔助裝置，可以準確識別出傷員。救援機器人配備有兩個機械臂，在救援過程中，救援機器人可以自行調整到適當位置，通過機械臂和輸送裝置的相互協調配合，將傷者安全平穩地以平躺姿勢傳送至一個小型的救援艙室中。

輪履復合變體輪是一種由驅動主輪、可變形履帶、伸展機構及傳動機構等組成的新型輪系。在較好的路況下，變體輪以輪式狀態行進以保證救援機器人具有較高的速度；在復雜地形下，變體輪可由內部伸展機構展開成三角履帶以達到高通過性的要求。圖1為變體輪工作原理圖。

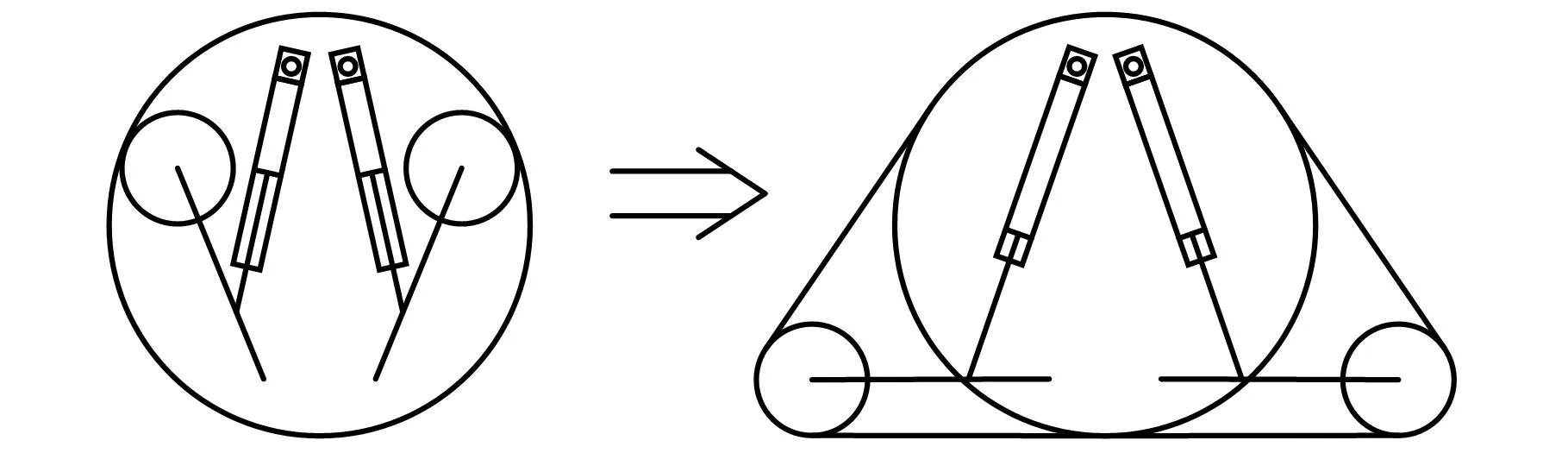
圖1　輪履復合變體輪原理圖

為實現輪履結構轉換，變體輪外側不同于普通充氣輪胎，而是由若干節分段的橡膠履帶節相互連接組成的近似圓形的“履帶輪”，實物如圖2所示。

圖2　履帶節示意圖

變體輪內部有復雜的機構，并且外側包覆有分段履帶，質量較一般車輪大且橡膠履帶較常見充氣輪胎剛度偏大。外側橡膠履帶結構的不連續性會產生未知激勵，對救援機器人的乘適性產生直接影響。

2　乘適性分析

乘坐舒適性可以用乘坐人員所感覺到的振動加速度作為評價指標[2]。在此建立救援機器人的振動模型并考慮救援機器人的結構特殊性，對其振動特性進行分析。

2.1救援機器人振動研究

輪履復合式救援機器人整體結構近似對稱于縱軸線，其模型可簡化為圖3所示的二分之一振動模型[4-5]。圖3中，下標f表示前橋，r表示后橋。

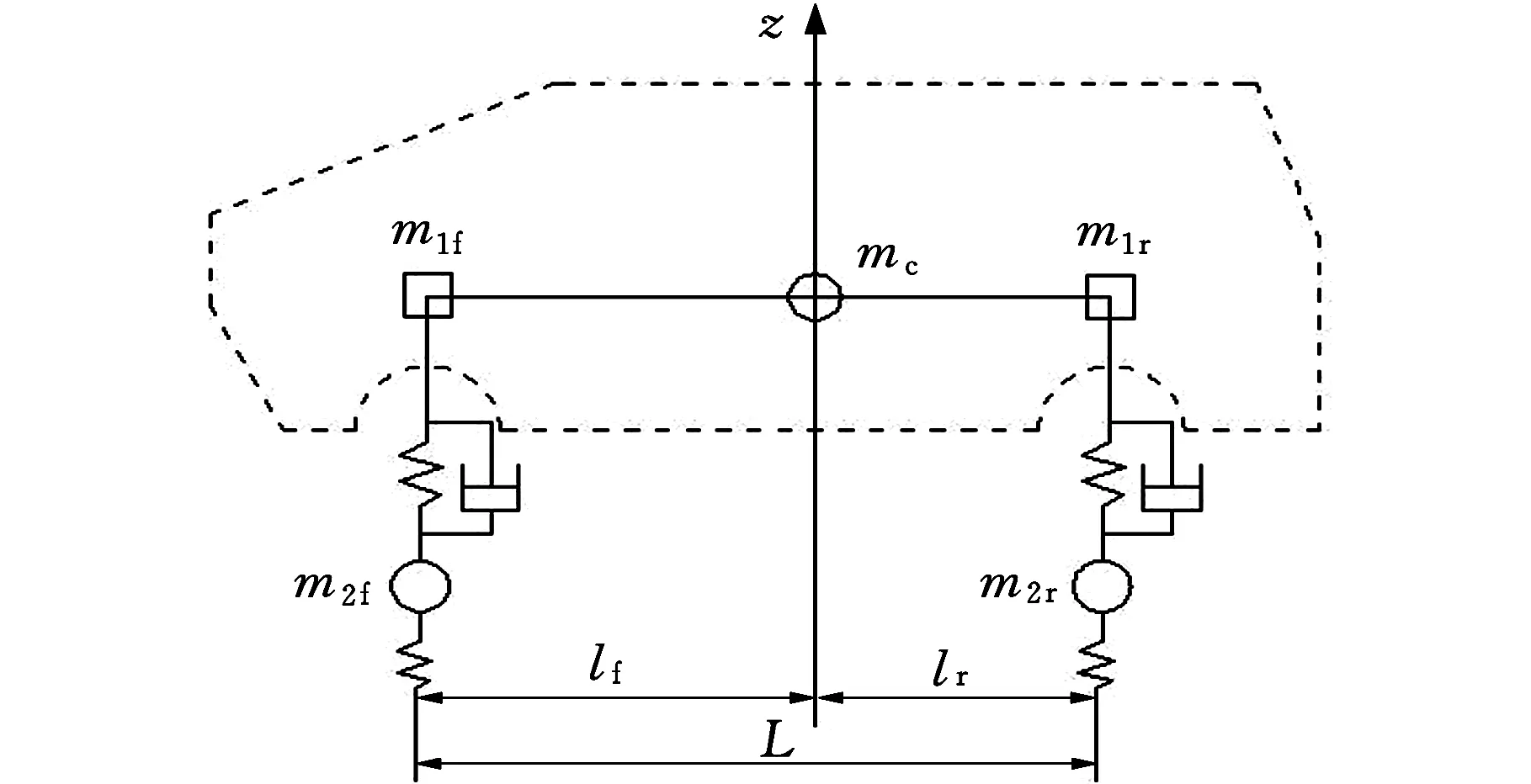
圖3　車體二分之一振動模型

車身質量可以等效為三個集中質量：前置質量m1f、聯系質量mc和后置質量m1r。根據動力學等效條件有：

(1)系統總質量保持不變，即m1f+mc+m1r=m1；

(2)質心位置不變，即m1flf-m1rlr=0；

可以計算得到三個集中質量分別為

(1)

車輪部分固有頻率為

(2)

其中，各量符號的意義及取值如表2所示。

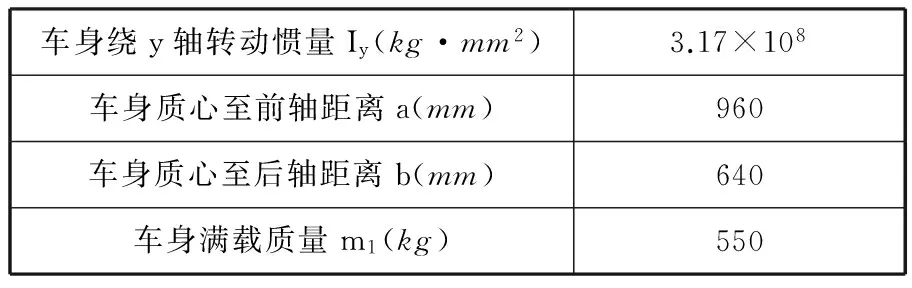
表1　救援機器人車身參數

表2　車體振動模型相關系數取值

將表2數據代入式(1)、式(2)可得：ωdf=9.0rad/s≈1.4Hz；ωaf=104.6rad/s≈16.6Hz；ωdr=8.7rad/s≈1.4Hz；ωar=105.0rad/s≈16.7Hz。

變體輪通過外側履帶與地面直接接觸，相應輪胎剛度較一般小型車輛的車輪剛度大，由計算得出車輪垂直跳動的固有頻率較一般車輛固有頻率(10Hz左右)高。對于常見路面，較高頻率時道路加速度輸入的幅值會有所增大[3]，在設計中應盡量保證較低的固有頻率以達到最佳隔振效果。所以應盡量減小履帶節剛度，實際中可以通過增加履帶外側掛膠層的厚度、減小橡膠的硬度以及改變履帶節外側的橡膠花紋形狀等方式實現。

變體輪外側履帶節之間的不連續可以看作是形狀的不完整，并且沿圓周方向均勻分布。該不完整度表現為車輪的徑向偏心，會對車軸產生徑向高階諧量激振力，該激振力階數等于外側履帶的節數。在此將此激振力作為外部激振，研究救援機器人的響應。該激振力的頻率為

(3)

式中，n為車輪轉速；v為車輪線速度；n′為激振力階數，n′=27；r為變體輪行駛半徑。

救援機器人行駛速度v取值范圍為15～60 km/h，則激振力頻率f的變化范圍為60～240 Hz。可以看出，車輪不連續性造成的激振力頻率范圍遠離車輪固有頻率(16.6～16.7 Hz)和車身固有頻率(1.3～1.4 Hz)，并且這種偏離與救援機器人的行進速度成正比。因此在救援機器人高速運行過程中，懸架系統可以將該激振力造成的振動較好地隔離。

2.2仿真模型構建

考慮到救援機器人實際運行工況多為瀝青、水泥硬路面，所以選取B級路面作為仿真路面。利用ADAMS/View建立仿真模型，如圖4所示。以機器人行駛方向為x軸，側向為y軸，垂直方向為z軸。對4個輪子同時添加驅動轉矩，使救援機器人速度穩定于50 km/h，作為觀測速度。

圖4　救援機器人仿真模型

考慮傷員以臥姿乘坐，在分析乘適性時應分別對傷員頭下、后背和盆骨三個直接接觸部位的支撐面進行測量[5]，分別定義該三個部位為A、B和C點，分別測量三點x、y、z軸向的加速度曲線。

2.3乘適性評價分析

對任意一點D點進行乘適性分析，對于D點i(i=x,y,z)軸加速度時間歷程aDi(t)有

則D點i軸方向頻率加權加速度均方根值為

(4)

其乘坐值(乘適性)分量avDi=KDiaWDi。其中，KDi為D點i軸軸向加權系數，對于人體的臥姿振動模型[6]，有KDx=KDy=KDz=1。

則D點的總乘坐值為

(5)

本文為了簡化計算，使用頻率加權函數濾波器對加速度的時域曲線進行濾波得到aWAi。

巴特沃斯濾波器具有合適的衰減陡度和很好的瞬態特性，且幅度響應帶內比較平緩，可以與頻率加權函數曲線較好地嚙合。用MATLAB設計巴特沃斯濾波器對加速度曲線進行濾波處理以替代加權方式。

國際標準化組織于1997年公布的ISO 2631-1:1997(E)《人體承受全身振動評價——第一部分：一般要求》中提到用加權均方根加速度的基本評價方法，并提供不同部位不同軸向的頻率加權函數曲線。參考標準知：B、C點垂直方向頻率加權系數為Wk，A、B、C點水平方向頻率加權系數為Wd，A點垂直方向頻率加權系數為Wj。

以垂直方向頻率加權系數Wk為例，對標準函數曲線與所設計的頻率加權函數濾波器的幅頻特性曲線進行對比，如圖5所示。可以看出，本文設計的濾波器與實際的加權標準有一定程度偏差，但很好地保留了對人體敏感的頻率帶2～12.5 Hz；高頻區域對人的主觀感覺影響不大，濾波器對高頻的阻斷對評價結果影響可以忽略[4]。對某時間段B點垂直加速度曲線進行濾波，如圖6所示。可以看出，垂直方向上通過帶通濾波器濾波后，保留了帶通部分中高頻率段的信號，濾波后的加權加速度時域曲線較濾波前的曲線密集。濾波前后的曲線對比很好地體現了帶通濾波器的特點。

(a)頻率加權函數的標準曲線(b)頻率加權函數濾波器幅頻特性曲線圖5　曲線對比

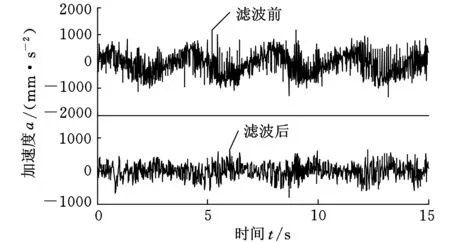
圖6　B點垂直方向濾波前后加速度曲線

2.4乘適性評價結果

(a)濾波前后x軸加速度(b)濾波前后y軸加速度

(c)濾波前后z軸加速度圖7　A點各軸方向濾波前后加速度曲線

以A點為例，其濾波前后加速度曲線如圖7所示。對濾波后加速度曲線作均方根值計算，可以得到A點三個軸向的乘坐值，如表3所示。

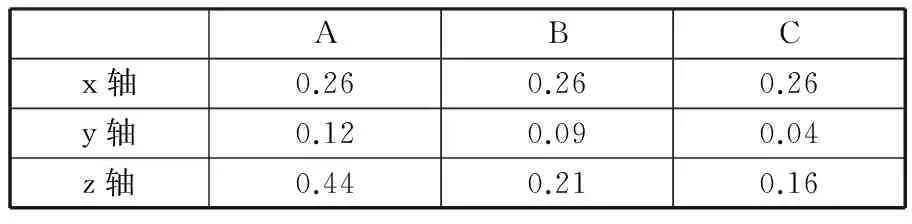
表3　各點各軸向的乘坐值　mm/s2

A、B、C點各軸向總乘坐值分別為

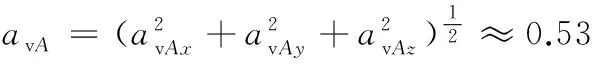
avB≈0.35m/s2

avC≈0.31m/s2

總乘坐值與人的主觀感覺的大致關系如表4所示。由計算結果可以看出， A、B、C點位置傷員的主觀感覺都會有一些不舒適，且以頭下(A點)部位感覺最差。因此有必要對救援機器人的懸架等參數進行優化以改善其乘適性。

表4　總乘坐值與人的主觀感覺的大致關系[7]

3　乘適性優化分析

3.1振動模型平順性分析

以懸架系統的參數為變量進行優化是為了獲取良好的平順性[8]，所以本文以A、B、C點的加速度作為優化對象。對于圖3所示模型，其受地面激勵的振動微分方程可以表示為

式中，I為轉動慣量；φ為車身俯仰角度；qf、qr分別為前后輪地面激振。

表示為矩陣形式為

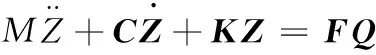
(6)

兩側取傅里葉變換得頻率響應函數矩陣：

(7)

以A點為例，設A點與救援機器人質心縱向距離為l，則A點垂直方向振動的頻率響應函數為

HA(ω)=Hs(ω)+lHp(ω)

(8)

A點相應的功率譜為

(9)

式(6)～式(9)中各量的含義請參考文獻[4]。其中，Sq(ω)為路面輸入功率譜密度，由于路面不平度對前輪與后輪的輸入不同步，有：

(10)

式中，n0為參考空間頻率，n0=0.1 m-1；Gq(n0)為路面不平度系數，對不同不平度等級路面有不同取值。

A點垂直方向加速度加權均方根值為

(11)

3.2優化設計

本文使用MATLAB優化工具箱進行優化設計[9]，以原始的懸架參數作為初始值，并根據實際懸架設計中的有關經驗及規定設置相關約束條件。

根據懸架設計中車輛滿載的懸架偏頻統計范圍，同時綜合考慮救援機器人的質心偏后側，前懸架剛度kf的取值范圍為14 200～30 500 N/m，后懸架剛度kr的取值范圍為17 400～32 000 N/m。另外，前后懸架系統動撓度的頻率響應函數為

Hf d(ω)=Hs(ω)+lfHp(ω)-Hf(ω)

(12)

Hrd(ω)=Hs(ω)+lrHp(ω)-Hr(ω)

(13)

同于式(9)，并考慮懸架擊穿的可能性，則懸架系統動撓度的均方根值需滿足：

(14)

(15)

式中，sf、sr分別為前后懸架動行程的容許值。

設置優化變量為

優化方程為

優化前后的懸架參數值如表5所示。

表5　優化前后懸架參數值

修改模型參數，再次仿真，結果如圖8所示。

(a)濾波前后x軸加速度(b)濾波前后y軸加速度

(c)濾波前后z軸加速度圖8　優化后A點各軸向濾波前后加速度

對曲線進行處理計算后，可得各點各軸向的乘坐值，如表6所示。則各軸向總乘坐值分別為：avA≈0.31 m/s2；avB≈0.28 m/s2；avC≈0.27 m/s2。

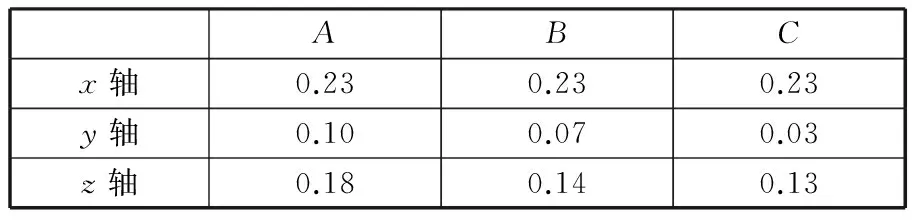
表6　優化后各點各軸向的乘坐值　mm/s2

4　討論

由以上計算結果可以看出，通過懸架參數優化后，A、B、C三點的總乘坐值均小于0.315 m/s2，傷員沒有感覺不舒適，救援機器人的乘適性得到了改善。

對比表3、表6數據，可以看出：①三個測試點行駛方向(x軸向)的乘坐值大體相同，但是由于三個測試點與救援機器人車身質心距離lA>lB>lC，A點橫向和垂直方向的加速度均較B、C點大。②救援機器人是近似對稱結構，各點橫向加速度相對較小，但是垂直方向的乘坐值均偏大，是影響救援機器人乘適性的關鍵因素。③以懸架參數作為變量進行優化，優化結果可通過直接改善救援機器人垂直方向的振動特性來改變各點垂直方向的乘坐值。

5　結論

(1)建立了救援機器人振動模型，分析了救援機器人的結構特殊性對其乘適性的影響。變體輪外側橡膠履帶的結構不連續性會引起徑向激振，通過計算，該激振力所產生的振動頻率范圍為60～240Hz，對機器人乘適性影響不大；但由于變體輪履帶節剛度過大，會使車輪部分固有頻率較常值偏大，使得較高頻率激振下的乘適性變差。

(2)針對救援機器人的綜合乘適性，以懸架參數作為優化變量，以三個關鍵測試點的總乘適性均方值作為優化目標進行優化分析，進一步的仿真分析結果顯示，優化后的懸架系數改善了救援機器人的乘適性，從而驗證了本文優化方法的正確性。

[1]劉金國，王越超，李斌,等.災難救援機器人研究現狀、關鍵性能及展望[J].機械工程學報，2006，42(12)：1-12.

LiuJinguo,WangYuechao,LiBin,etal.CurrentResearch,KeyPerformancesandFutureDevelopmentofSearchandRescueRobot[J].JournalofMechanicalEngineering, 2006,42(12):1-12.

[2]羅洋，李奇敏，溫皓宇,等.一種新型輪腿式機器人設計與分析[J].中國機械工程，2013，24(22)：3018-3023.

LuoYang,LiQimin,WenHaoyu,etal.DesignandAnalysisofaNewKindofWheel-leggedRover[J].ChinaMechanicalEngineering, 2013,24(22):3018-3023.

[3]GillespieTD. 車輛動力學基礎[M].趙六奇，金達鋒,譯.北京：清華大學出版社，2006.

[4]張立軍，何輝.車輛行駛動力學及應用[M].北京：國防工業出版社，2011.

[5]李曉玲，張鄂，陸長德,等.人體生物力學模型的駕駛舒適度仿真研究[J].西安交通大學學報，2008，42(5)：556-560.

LiXiaoling,ZhangE,LuChangde,etal.DrivingComfortSimulationBasedonHumanBiomechanicsModelunderVibration[J].JournalofXi’anJiaotongUniversity, 2008,42(5):556-560.

[6]蘇琛，徐新喜，高振海,等.某履帶急救車減振效率及乘臥舒適性分析[J].振動、測試與診斷，2012，32(5)：854-857.

SuChen,XuXinxi,GaoZhenhai,etal.TheAnalysisofaTrackedAmbulanceDampingEfficiencyandRideComfort[J].JournalofVibrationMeasurement&Diagnosis, 2012,32(5):854-857.

[7]丁法乾.履帶式裝甲車輛懸掛系統動力學[M].北京：國防工業出版社，2004.

[8]王德平，郭孔輝，宗長富,等.車輛動力學穩定性控制的理論研究[J].汽車工程，2000，22(1)：7-9.

WangDeping,GuoKonghui,ZongChangfu,etal.TheoreticalStudyonVehicleDynamicsStabilityControl[J].AutomotiveEngineering, 2000,22(1):7-9.

[9]BouazaraM,RichardMJ.AllOptimizationMethodDesignedtoImproveVehicleComfortandRoadHoldingCapabilitythroughtheUseofActiveandSemi-activeSuspensions[J].EuropeanJournalofMechanicsandSolids, 2001,20(3):509-502.

(編輯袁興玲)

Analysis and Optimization of Ride Comfort for a Wheel-tracked Rescue Robot

Li Hao1,3Shi Caihong3Kang Shaohua2Zhang Xizheng3

1.Tianjin University of Technology,Tianjin,300384 2.Military Traffic Institute,Tianjin,300161 3.Academy of Military Medical Science,Tianjin,300161

This paper presented a new kind of wheel-tracked rescue robot,which could efficiently search and transport the wounded in the disaster sites and other complex environments by converting the structure between wheel and track. Considering the safety and comfort of the wounded,this paper focused on the vibration analysis during the transporting of the wounded, and used the multi-body dynamics software ADAMS to establish the rescue robot’s dynamics model.This model was about the simulation analysis of the operation in the actual road conditions. Considering different parts of the human body have different frequency weighting functions in different directions, the simulation curve should be processed by the corresponding filter designed by MATLAB to calculate the robot’s ride comfort. Target to better ride comfort, the suspension parameters should be redesigned by the MATLAB optimization toolboxes.And the further simulation outcomes demonstrate the rationality of the optimization results.

wheel-tracked; dynamics analysis; ride comfort; optimization design

2014-07-09

軍隊重大專項(BS312C002)；軍事醫學科學院創新基金資助項目(2012CXJJ007)

TP242.6< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.11.005

李浩，男，1991年生。天津理工大學與軍事醫學科學院聯合培養碩士研究生。主要研究方向為機械設計及理論。侍才洪，男，1982年生。軍事醫學科學院衛生裝備研究所助理研究員。康少華，女，1959年生。軍事交通學院軍事物流系教授。張西正，男，1955年生。軍事醫學科學院衛生裝備研究所研究員、博士研究生導師。