多桿高速機械壓力機機構優化設計

李燁健　孫　宇　胡峰峰

南京理工大學，南京，210094

多桿高速機械壓力機機構優化設計

李燁健孫宇胡峰峰

南京理工大學，南京，210094

為了有效發揮壓力機的性能、解決機械壓力機高速化帶來的一系列問題，建立了一種以曲柄最短、沖壓轉角最大為評價指標的多桿高速機械壓力機主傳動機構幾何參數綜合優化數學模型，并利用MATLAB構建了該機構的優化模型。優化結果表明：該機構的沖壓轉角增大了13.5%，主滑塊加速度減小了35.3%，在下死點附近，位移曲線較平滑，有利于沖裁過程中材料的充分變形和動平衡的設計，且有助于提高下死點的動態精度。

高速壓力機；多桿機構；優化設計；運動軌跡

0　引言

近年來，隨著電子、通信及汽車工業的迅猛發展，市場對沖壓零件的需求量迅速增大，為了滿足市場對沖壓零件的需求，世界各國都在不斷地提高壓力機的速度[1-3]。然而，如何解決高速化給機構幾何參數優化帶來的一系列問題，充分發揮壓力機的工作性能，使其高效地工作已成為人們非常關注并重點研究的課題。目前，國外對高速壓力機傳動機構的研究相對較成熟，如瑞士的Bruderer公司、美國的Minster公司都進行了深入研究并開發出相關產品[4-5]。近年來，國內有學者以下死點附近的滑塊速度及其波動、曲柄驅動扭矩、速度和加速度誤差、機構高度以及機構壓力角或傳動角等為評價指標，利用GA、SQP、SLP等算法以及步長搜索法對壓力機八桿內滑塊機構進行了優化，利用ANSYS、ADAMS的Insight功能模塊對主傳動系統各桿件幾何參數進行優化，提高了設計的效率[6-9]。上述研究的研究對象均為低速壓力機傳動機構，幾何參數優化的評價指標不一定適用于對高速壓力機機構幾何參數的評價。對于幾何參數常規設計方法，首先給定機構的某些參數，然后利用作圖法或解析法不斷修改設計參數，直至得出滿意的曲柄長度和連桿長度，重復工作量大，精度不高，設計的結果是唯一的，但不一定是最佳的。機構的運動規律與連桿機構的幾何參數之間存在錯綜復雜的非線性關系，尋找一組滿足各約束的機構幾何參數有一定的困難[10]。目前，高速壓力機的多桿主傳動機構仍較復雜，存在構型種類繁多、設計理論不夠完善和性能低等亟需解決的問題。因此，尋找合適的機構優化評價指標已成為高速壓力機機構優化設計的關鍵問題。

為了提高壓力機的工作性能，得到最優的工作曲線，降低后續設計的難度，本文根據多桿高速機械壓力機的性能要求，以曲柄最短和沖壓轉角最大為評價指標，對研發中的多桿高速機械壓力機機構幾何參數進行優化設計。

1　機構模型的建立

多桿高速壓力機傳動機構原理示意圖見圖1。該機構主要由機架、對心曲柄滑塊機構、拉桿、上下肘桿和主滑塊組成。曲柄勻速圓周轉動，通過連桿帶動副滑塊沿導軌在豎直方向運動，副滑塊的豎直運動使拉桿上下擺動，從而使肘桿左右擺動，實現主滑塊沿導軌的直線往復運動。在該機構中，肘桿可以放大驅動力，同時肘桿吸收了壓力機工作時的大部分沖壓載荷，避免電機直接受到工作載荷的沖擊，使其運行平穩。

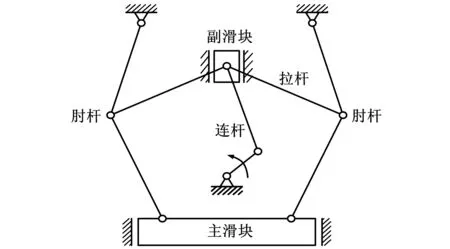
圖1　多桿高速壓力機原理示意圖

2　多桿壓力機的優化設計

一般的優化問題是在d維歐氏空間中尋找一個點x=(x1,x2,…,xd)T，在滿足gi(x)≤0和hj(x)=0約束條件時，使f(x)取最小值。上述優化問題可簡寫為

式中，f(x)、gi(x)、hi(x)為d元函數；f(x)為目標函數；gi(x)為不等式約束條件；hi(x)為等式約束條件；x為設計變量。

2.1設計變量

為表述方便，建立圖2所示的單邊傳動機構及坐標系，坐標原點位于曲柄的旋轉中心O0，x軸正向為水平向右，y軸正向為垂直向上。圖2中，m為上肘桿與機身上鉸點水平距離；h為上肘桿與機身上鉸點垂直距離；n為主滑塊寬度尺寸。

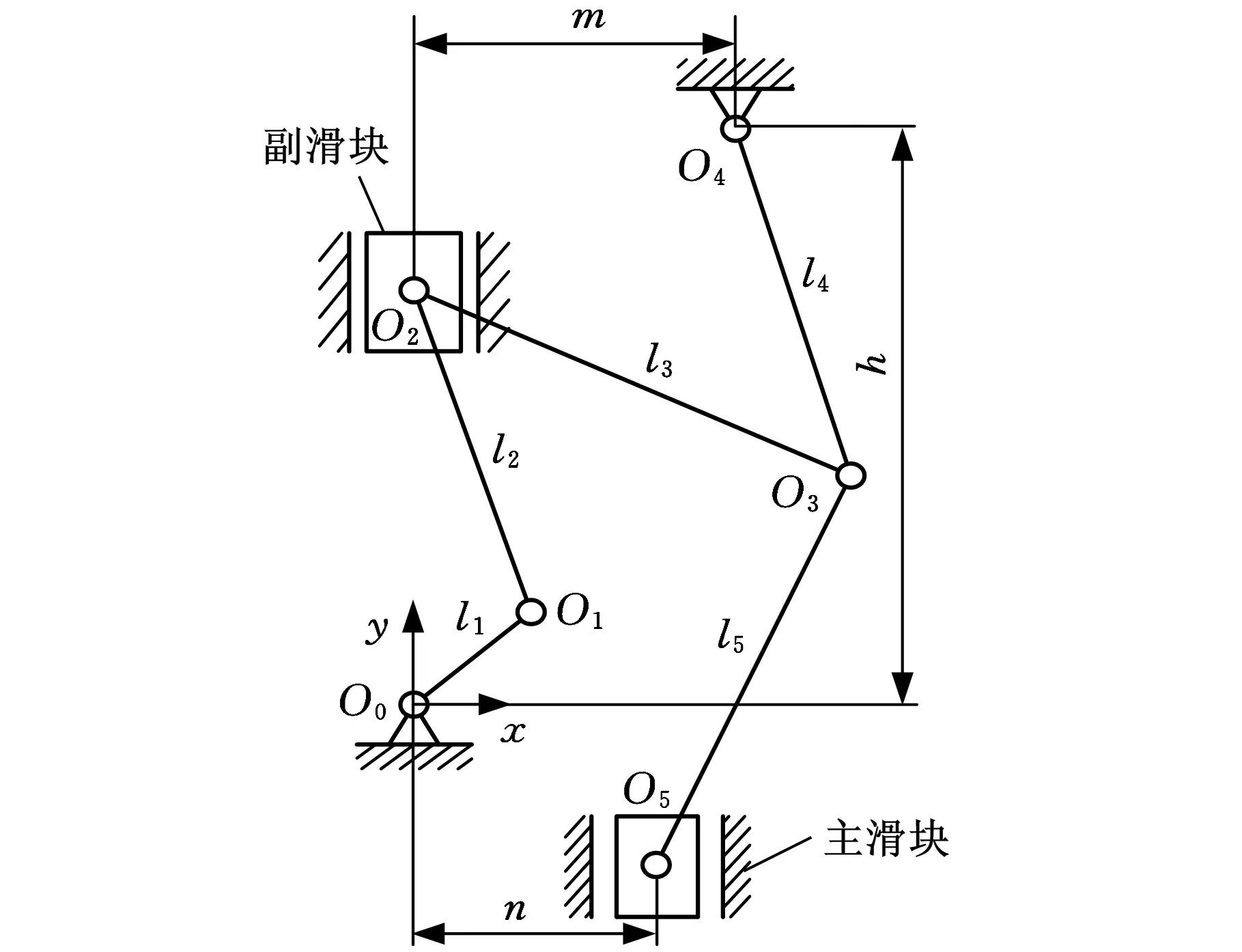
圖2　單邊傳動機構

對圖2進行運動分析可知，決定該多桿機構運動規律的幾何參數有曲柄長度l1，連桿長度l2，拉桿長度l3，上下肘桿長度l4、l5，主滑塊鉸點位置參數n和上鉸點位置參數m、h。因此，該多桿壓力機傳動機構的獨立設計參數共8個，故設計變量定義為

X=(x1,x2,x3,x4,x5,x6,x7,x8)T=

(l1,l2,l3,l4,l5,m,n,h)T

2.2目標函數

高速壓力機主要用于落料和沖孔，工作在使工件產生彈性變形、塑性變形和斷裂分離3個階段，并且工作速度較高，沖裁時間較短，主滑塊的工作特性對零件精度的影響至關重要。

為了使壓力機得到較理想的運動規律輸出，滿足沖壓工藝的要求，在給定設計要求的前提下，應合理確定壓力機傳動機構的評價指標。為提高經濟性以及機床工作性能，本文提出了各桿長之和應最小、有較長的沖壓時間、各桿件受力狀況合理、主滑塊速度波動及加速度應盡量小等設計要求。一般地，低速拉伸壓力機只工作在使工件產生彈塑性變形階段，對主滑塊的工作速度和速度波動有一定限制，防止工件產生裂紋，以提高產品質量。

曲軸是機構的原動部分，其運行精度對下死點的運行精度有直接影響，對于高速壓力機，熱變形是無法忽略的。曲軸部位是整機的主要發熱源，極易產生熱變形，曲柄受力是影響發熱的主要因素。曲柄長度與曲柄受力成正比，因此，應優化曲柄長度，以限制曲軸受力，從而減少曲軸發熱，減小原動件的熱變形，提高主滑塊運行精度；同時也有助于減小驅動電機負載和轉速波動，降低機構動平衡的設計難度，提高系統的可靠性和產品質量。

由壓力機的實際工況和對機構的運動學分析可知，增大沖壓轉角，從而延長工件在沖壓過程中的變形時間，使工件變形充分，機構的受力更加均勻，減小沖擊，有助于提高機構的魯棒性和產品的質量[11]。

機構的評價指標直接指引優化算法的搜索方向，所以在建立機構的評價指標時，合理確定優化目標函數非常重要。在機構的建模中，有學者直接以滑塊速度最小、滑塊速度波動最小、各桿長之和最小等為優化目標，利用加權系數法將它們組合成一個多目標函數。此時，滑塊的速度波動、速度和桿的長度量綱是不一致的，而且它們的數量級相差也較大，在優化求解過程中，數量級大的優化目標分量會過于“強勢”，極易出現“大數吃小數”的現象，最終難以得到滿意結果。為了解決上述問題，本文對各個優化目標分量進行歸一化處理，然后累加作為綜合優化目標函數，解決了量綱不一致和數量級相差較大的問題。

某些優化目標在優化求解過程中，優化算法會干擾優化的搜索方向，會一味地沿著減小優化目標值的方向搜索，破壞機械壓力機的傳動角、相對位置等設計要求，難以得到良好的機械壓力機設計方案。本文將這些優化目標轉換為相應的約束函數來處理，減小其對總體性能的影響，保證壓力機具有良好的綜合性能。

綜上所述，本文以減小曲軸受力、增大沖壓轉角作為優化目標，多桿壓力機主轉動機構的綜合優化目標函數為

f(X)=l1/lc+φc/(φe-φs)

(1)

其中，lc為曲柄的優化目標長度，取20 mm；φe、φs分別為公稱力行程結束和開始時對應的曲柄轉角；φc是沖壓轉角的優化目標值，取0.5π。

2.3約束條件

對于給定的一種多桿高速壓力機原理機構形式，與其匹配的機構參數有很多，但不是所有與其匹配的參數都能夠作為壓力機傳動機構的工程化參數，需要綜合考慮機構運動干涉、滑塊行程、各桿件長度、機構高度及傳動角等性能指標，同時結合機構成立的約束條件，建立機構工程化設計的約束條件[12-15]。約束條件如下。

(1)由于機身結構尺寸和裝配需要的限制，需要對各構件長度和相對位置參數進行約束，不等式約束條件為

(2)

(2)為保證機構能正常運轉以及裝配和受力的需要，建立曲柄存在條件：

g3(X)=l1-l2+l≤0

(3)

式中，l為保證裝配和受力需要選定的許用值，本文取260 mm。

(3)為保證整機的穩定性，需限制上梁的高度，則位置參數h的約束條件為

g4(X)=h-hmax≤0

(4)

式中，hmax為允許的上鉸點最大高度。

(4)為保證主副滑塊能正常運動，滑塊可動的約束條件為

(5)

g6(X)=xO3-n-l5≤0

(6)

式中，xO3為O3點x坐標。

(5)為改善傳動機構的受力狀況，保證機構的正常運轉和傳力特性，減小工作過程中主軸和曲柄的受力，需使各點滿足壓力角的約束條件：

g7(X)=φ-φmax≤0

(7)

式中，φmax為允許的最大壓力角，一般取40°～45°。

(6)為保證原理機構能實現預定的功能以及設計的合理性，當主滑塊處于上死點位置時，拉桿不能處于水平姿態。

參照圖2可得，當主滑塊處于上死點位置時，拉桿與水平方向的夾角最小。此時，O2點坐標為(0,l2-l1)，圖3中A點坐標為(0,h)，O4點坐標為(m,h)。

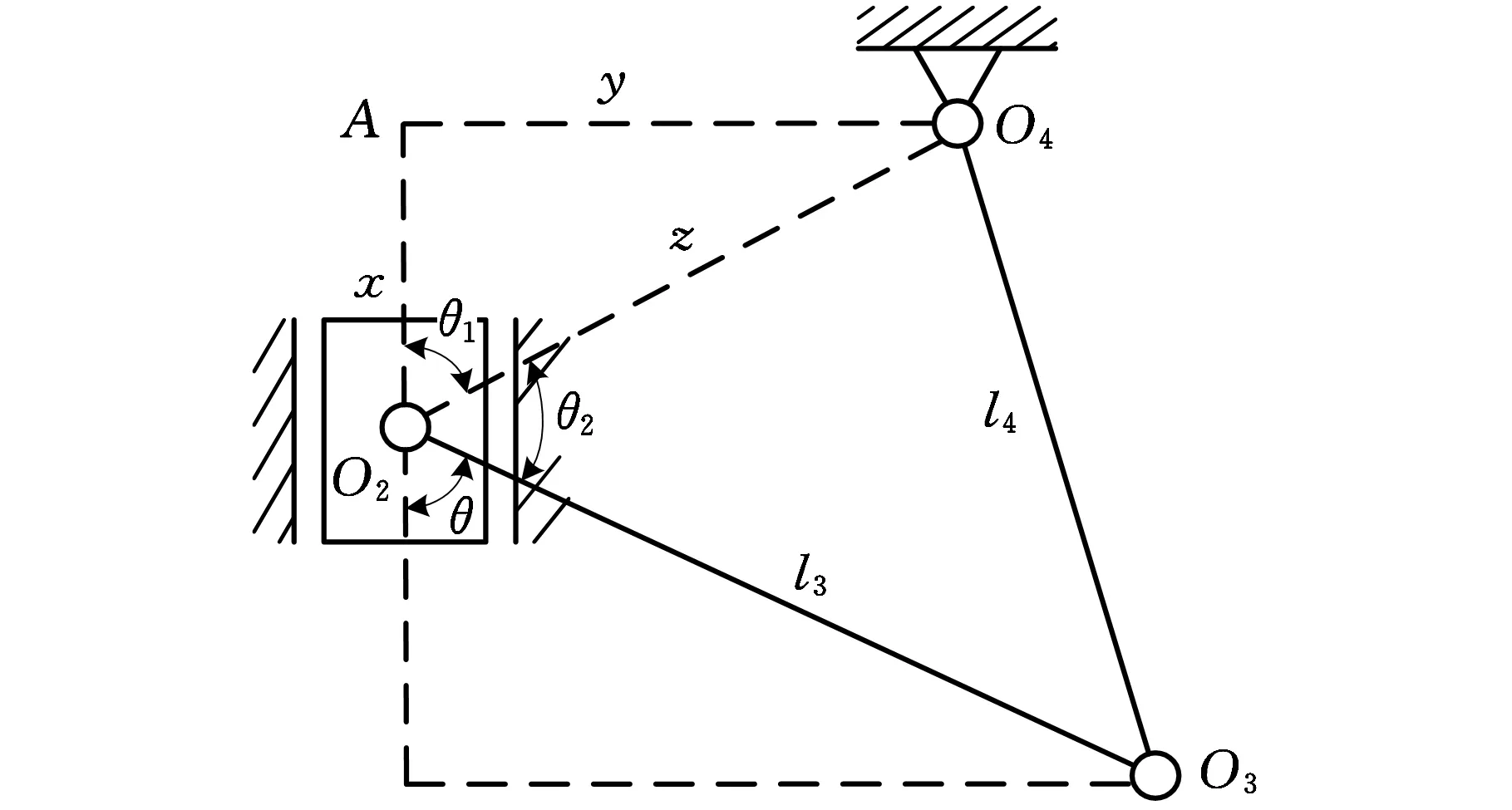
圖3　拉桿約束簡圖

參照圖3，并根據各點的位置關系可得

(8)

tanθ1=m/(h-l2+l1)

(9)

(10)

θ=π-(θ1+θ2)

(11)

由拉桿不能處于水平位置，建立姿態約束條件：

g8(X)=π/2-(θ1+θ2)≤0

(12)

(7)為了適應運動副間隙和零件的受力變形，使機構運行可靠且不出現奇異位形，當主滑塊處于下死點位置時，必須保證O3點在O4與O5點連線的外側。

參照圖2，根據各桿件的配置方式，當主滑塊處于下死點位置時，上下肘桿趨向于共線狀態，所以只需約束該狀態，即可使上下肘桿不出現共線狀態。由圖4可得，O2點坐標為(0,l1+l2)，A點坐標為(0,h)，O4點坐標為(m,h)。

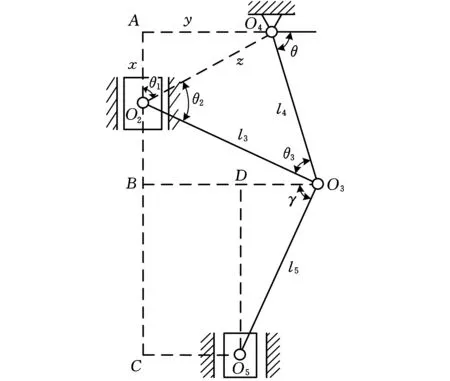
圖4　上下肘桿約束簡圖

根據各點的位置關系可得

(13)

tanθ1=y/x=m/(h-l2-l1)

(14)

(15)

(16)

cosγ=(l3sinθ-n)/l5

(17)

θ=(θ1+θ2+θ3)-π/2

(18)

γ<π-θ

(19)

根據式(19)，建立不等式約束條件：

g9(X)=-cosγ-sin(θ1+θ2+θ3)≤0

(20)

根據加工要求，為保證連桿孔中心距的加工精度，各桿件幾何參數必須是整數。在優化程序中加入整數約束條件，可以消除小數圓整帶來的誤差。2.4優化計算及結果

以正在研發中的某機械式多桿高速壓力機單自由度主傳動機構為例，考慮其主要用途，根據其主要工藝要求對設計機構的幾何參數和運動參數進行多目標綜合優化，并與一般機械式高速壓力機主傳動機構的傳動性能進行對比，以驗證優化的正確性與合理性。該壓力機主傳動機構的主要技術參數如下：公稱壓力為600kN，公稱壓力行程為3mm，滑塊行程為20mm，主滑塊最大工作頻率為1000次/min。

機械壓力機的多桿機構較復雜(桿件數目較多)，且對運動具有較高的要求，采用傳統的綜合方法效率較低，也不易滿足良好的機構綜合性能要求。步長搜索法方便易懂，其算法比GA算法、蟻群算法和遺傳算法等算法簡單，而且可以很好地控制搜索的范圍和步長，編程容易，該算法幾乎搜遍了全部的解，較容易得到最優解，但是該算法具有較高的時間復雜度，隨著計算機技術的發展，該問題已經得到很好的解決，所以本文采用步長搜索法解決多桿機械壓力機主傳動機構的優化問題。

設計者依據知識和經驗給定各參數的取值范圍，指定參數變化的優先順序，確定步長，將設計變量逐一離散化。設計變量共8個，設計變量的離散數最大為k，則可以得到一個用8k階矩陣表示的變量空間(定義域)S，其中k值的大小直接關系到算法的時間復雜度，所以k值可以先取一個相對較小的值，得到一個最優解，在此基礎上k再取較大值，就可以獲得較低的時間復雜度。然后在空間S中根據給定的步長搜索，依次從空間下界循環至空間上界，直至最后一個循環中止為止，即遍歷空間S的每一組參數。

在對空間S的搜索過程中，并不是所有的點都滿足機構運行的約束條件和工程可行性條件。因此，首先對空間中的所有點根據約束條件g1(X),g2(X),…,g9(X)進行判斷，滿足條件則繼續，否則不予計算，進而判斷式(1)中的機構性能評價指標f(X)是否取得最小值，直至搜索到空間S的上界。圖5為利用步長搜索法對多桿機構優化設計的流程圖，其中，stp為步距。

根據上述主要技術參數，利用MATLAB編寫優化程序，通過優化得到各桿件的幾何參數，即設計變量X的最優解為

X*=(18,300,252,200,248,197,31,316)T

通過運動學分析，得到運動學曲線，如圖6～圖8所示。

圖6所示為兩種結構主滑塊位移曲線，由圖6可知，多桿結構的沖壓轉角(0.88rad)較一般結構的沖壓轉角(0.78rad)增大了13.5%，沖壓轉角的增大使工件材料的變形時間延長，有助于工件材料的充分變形，提高了工件的品質，同時也使機構受力均勻，減小了機構中各構件間的沖擊，從而減小了振動。

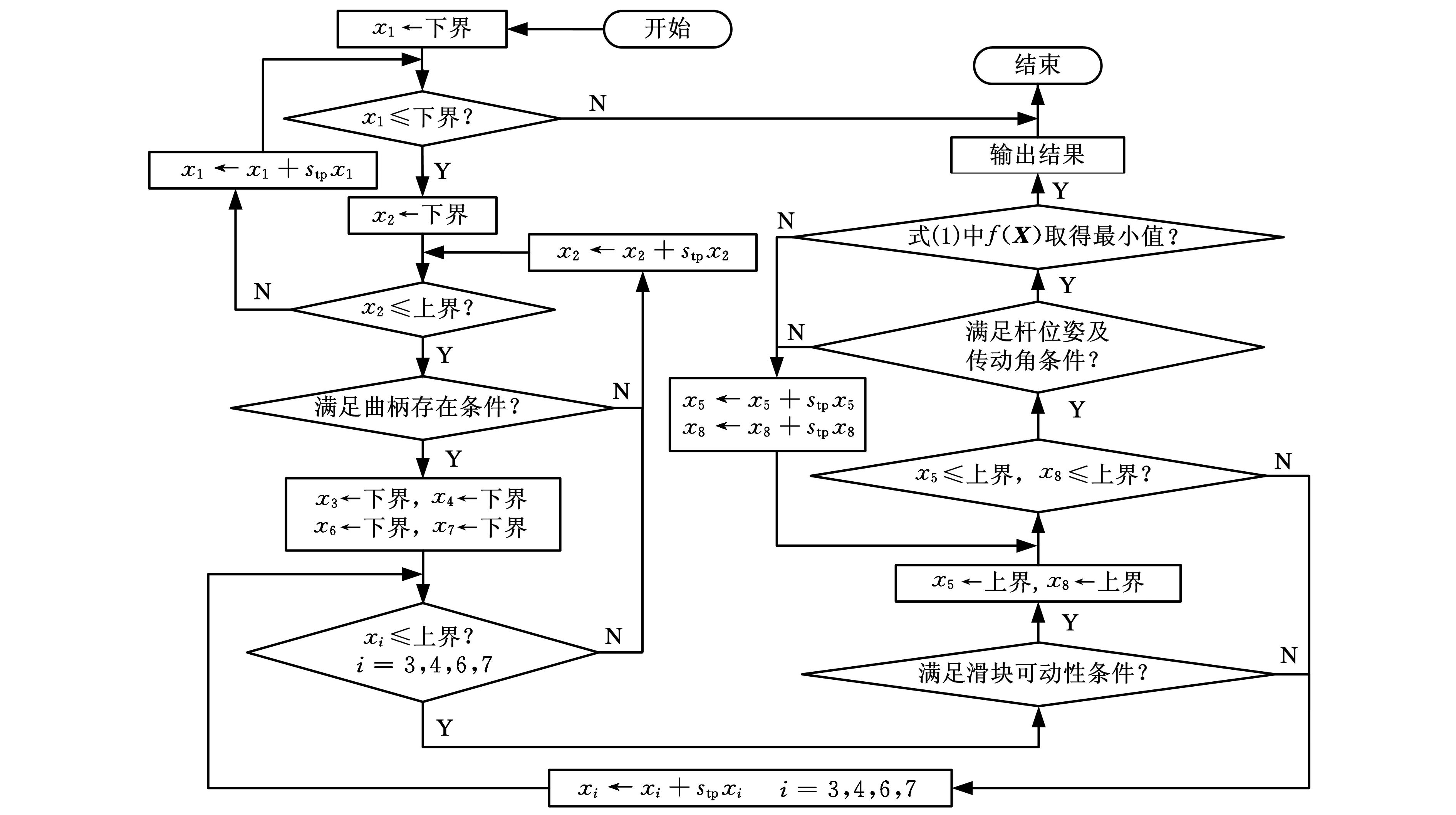
圖5　多桿機構優化流程圖

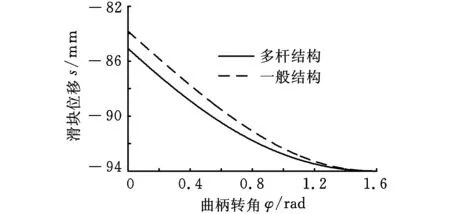
圖6　位移曲線

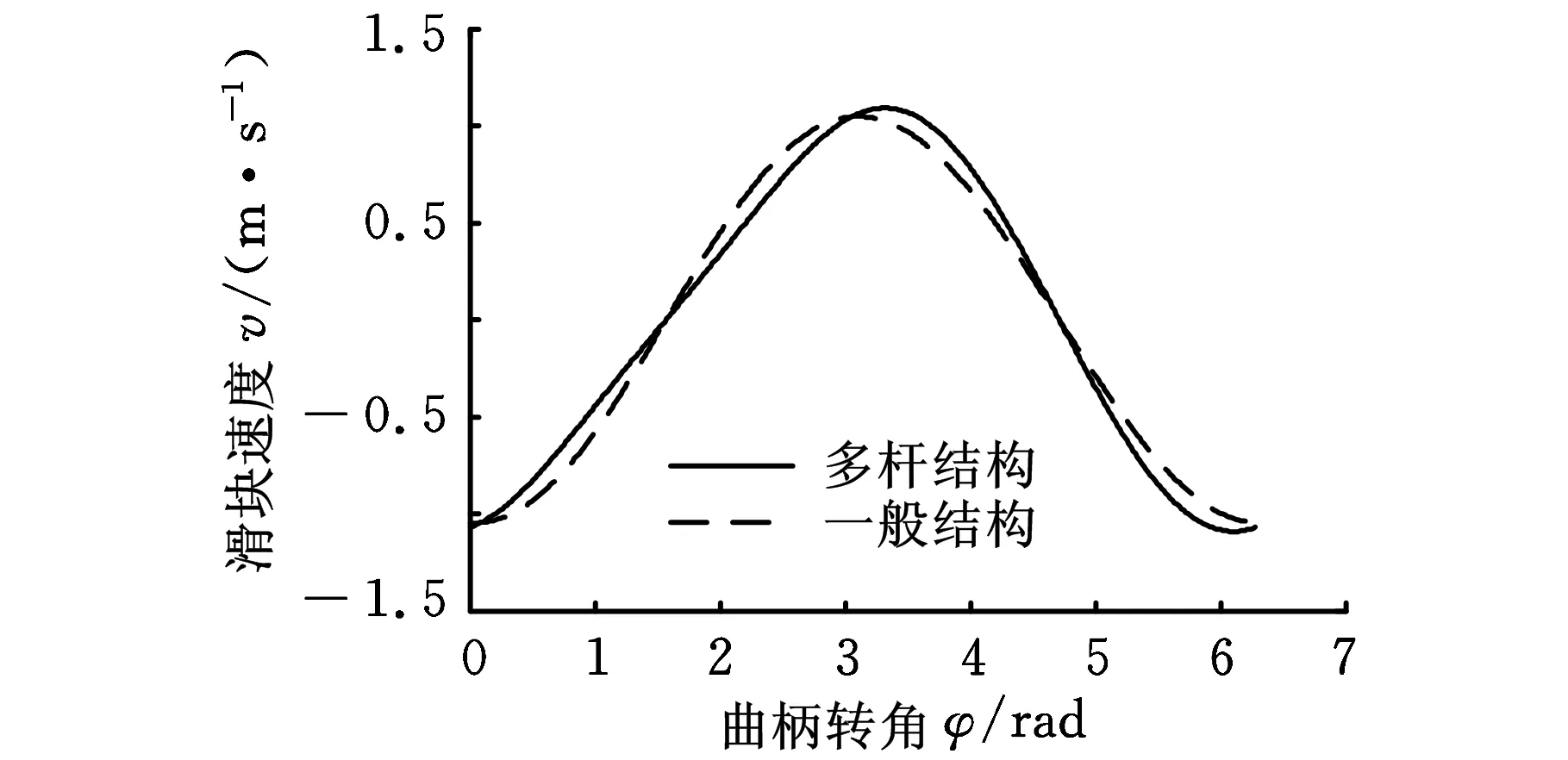
圖7　速度曲線

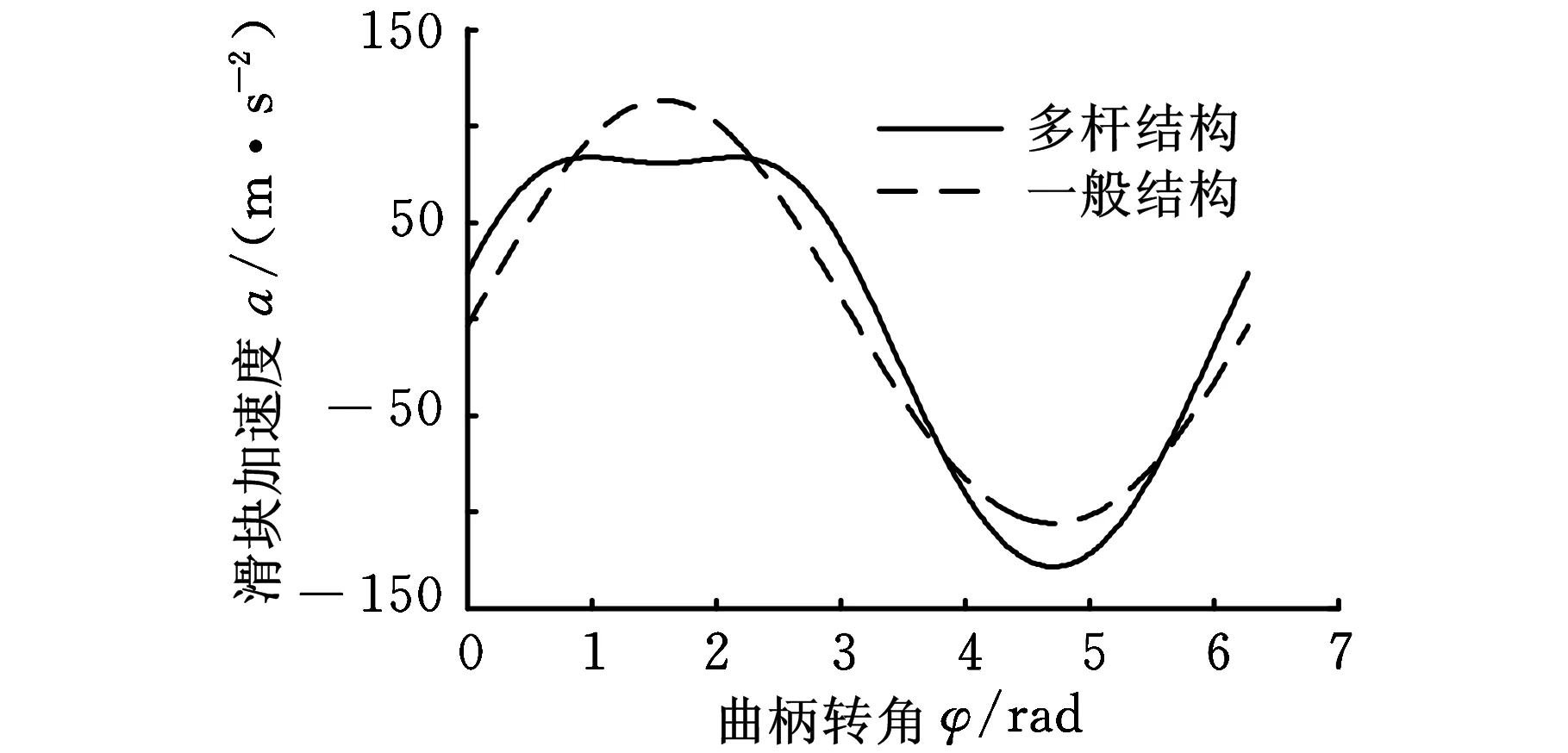
圖8　加速度曲線

圖7所示為兩種結構主滑塊速度曲線，由圖7可以看出，在0～π段，多桿結構速度曲線的斜率較一般結構的斜率小，速度波動較小，上模接觸金屬帶料時的速度較低，有助于減小沖擊和噪聲，從而提高壓力機的壽命。多桿結構主滑塊最大速度較一般結構主滑塊最大速度增大了4.1%，該最大值在0.5π～1.5π段回程階段內，從而縮短了回程時間。

圖8所示為兩種結構主滑塊加速度曲線，由圖8可知，多桿結構主滑塊加速度較一般結構主滑塊加速度減小了35.3%，系統慣性力減小，為動平衡的設計減小了難度，提高了主滑塊運動精度，進一步提高了加工的成品率。在下死點附近，多桿結構的主滑塊加速度變化較小，近似于保持一定值，這表明主滑塊慣性力近似于定值，在壓力機沖壓階段主滑塊以相對恒定的沖壓力沖壓工件，上模在接觸帶料時接觸速度減小，加速度和沖壓力趨于穩定，從而減小了整機的振動和沖壓階段的沖擊，保證了主電機和模具的壽命，以及產品的加工精度。

3　結論

(1)本文通過分析，給出了多桿高速機械壓力機的原理傳動機構，并建立了機構的多目標優化數學模型，提出了將曲柄長度和沖壓轉角作為綜合評價機構性能優劣的指標。

(2)優化分析結果表明，曲柄長度較小，減小了曲軸的受力和發熱，有利于提高機器的運行速度。公稱力行程范圍內，曲柄轉角增大了13.5%，下死點附近位移曲線較平滑，有利于材料的充分變形，利于沖裁。主滑塊最大速度增大了4.1%，主滑塊最大加速度減小了35.3%，有利于減小機床的振動，提高下死點動態精度。

研究結果為多桿高速機械壓力機主傳動機構幾何參數和運動參數的優化設計提供了參考。

[1]曾梁彬,孫宇,彭斌彬. 基于動態響應的高速壓力機綜合平衡優化[J].中國機械工程,2010, 21(18): 2143-2148.

ZengLiangbin，SunYu，PengBinbin.SyntheticDynamicBalanceOptimizationofHighSpeedPunchBasedonDynamicResponse[J].ChinaMechanicalEngineering, 2010, 21(18): 2143-2148.

[2]趙升噸,張學來, 高長宇，等.高速壓力機慣性力平衡裝置及其特性研究(一)[J].鍛壓設備與制造技術,2005,40(4):27-30.

ZhaoShengdun,ZhangXuelai,GaoChangyu，etal.InvestigationonInertialForceBalanceAssemblyUnitsandTheirDynamicCharacteristicsofaHighSpeedPress[J].ChinaMetalFormingEquipment&ManufacturingTechnology,2005,40(4):27-30.

[3]AzpilgainZ,OrtubayR,BlancoA,etal.Servo-mechanicalPress:aNewPressConceptforSemi-solidForging[J].DiffusionandDefectData:PartBSolidStatePhenomena, 2008, 141/143(3): 261-266.

[4]溫慶普.BRUDERER高速沖壓技術的優勢[C]//第四屆中國國際金屬成形會議論文集.上海,2008.

[5]HongDK,WooBC,KangDH.ApplicationofFractionalDesignforImprovingPerformanceof60WTransverseFluxLinearMotor[J].JournalofAppliedPhysics, 2008, 103(7):1-3.

[6]王曉麗,周天源.壓力機八桿內滑塊機構的優化設計[J].農業機械學報, 2007, 38(12): 232-234.

WangXiaoli,ZhouTianyuan.TheOptimizationDesignofInnerSlidingBlockMechanismofEight-barLinkageforPress[J].TransactionsoftheChineseSocietyofAgriculturalMachinery, 2007, 38(12): 232-234.

[7]陳岳云. 多連桿伺服壓力機動態性能分析與設計研究[D].上海:上海交通大學, 2008.

[8]李初曄,孫彩霞,鄭會恩. 基于ANSYS的多連桿機構性能優化[J].鍛壓技術,2011,36(6):80-83.

LiChunye,SunCaixia,ZhengHuien.PerformanceOptimizationofMulti-linkageMechanismBasedonANSYS[J].Forging&StampingTechnology,2011,36(6):80-83.

[9]劉海彬. 基于ADAMS的多連桿壓力機參數化設計與優化研究[D].青島:山東科技大學, 2011.

[10]楊春峰,張盛,李云鵬，等. 機械壓力機六連桿機構優化設計[J].大連理工大學學報,2013,53(1): 64-70.

YangChunfeng,ZhangSheng,LiYunpeng，etal.OptimizationDesignforSix-barLinkageofMechanicalPress[J].JournalofDalianUniversityofTechnology,2013,53(1): 64-70.

[11]謝嘉, 趙升噸,梁錦濤，等.壓力機桿系優化求解的變量循序組合響應面法[J].西安交通大學學報,2012,46(5):57-62.

XieJia,ZhaoShengdun,LiangJintao，etal.VariableSequentialCombinationResponseSurfaceMethodologyforPressRodSystemOptimization[J].JournalofXi’anJiaotongUniversity,2012, 46(5):57-62.

[12]李輝,張策,孟彩芳. 基于正運動學分析的混合驅動壓力機優化設計[J].中國機械工程,2004, 15(9): 771-774.

LiHui,ZhangCe,MengCaifang.OptimumDesignofHybrid-drivenMechanicalPressBasedonForwardKinematicsAnalysis[J].ChinaMechanicalEngineering,2004, 15(9): 771-774.

[13]ShangWanfeng,ZhaoShengdun,ShenYajing.AFlexibleToleranceGeneticAlgorithmforOptimalProblemswithNonlinearEqualityConstrains[J].AdvancedEngineeringInformatics, 2009, 23(6): 253-264.

[14]宋清玉,李建, 殷文齊. 基于多目標的機械壓力機六連桿機構設計[J].農業機械學報,2012, 43(4): 225-229.

SongQingyu,LiJian,YinWenqi.MechanicalPressSix-linkMechanismDesignBasedonMulti-objective[J].TransactionsoftheChineseSocietyofAgriculturalMachinery,2012, 43(4): 225-229.

[15]林偉慶,李振石,李建平，等. 基于遺傳算法的多連桿壓力機運動優化方法[J].鍛壓技術,2011, 36(5): 81-84.

LinWeiqing,LiZhenshi,LiJianping，etal.OptimizationMethodforMovementofMulti-barPressBasedonGeneticAlgorithm[J].Forging&StampingTechnology,2011, 36(5): 81-84.

(編輯陳勇)

Optimization Design for Multi-linkage of High-speed Mechanical Press

Li YejianSun YuHu Fengfeng

Nanjing University of Science and Technology,Nanjing,210094

In order to exert the ability of press, and solve a series of problems of high-speed mechanical press, an compound optimal mathematic model about geometric parameters of main driving organization of high-speed mechanical press was established, which took minimum of crack and maximum of punching angle as the evaluation index. In the meantime, the optimal model was established with MATLAB. The optimization results show that the punching angle of organization is increased by 13.5%, and acceleration of main slider is decreased by 35.3%. The displacement curve is smooth in the near of bottom dead center. It is beneficial to a bundant deformation of materials in the process of stamping, the design of dynamic balance, and to improve the dynamic precision of the bottom dead center.

high-speed press; multi-linkage; optimization design; motion path

2013-08-20

國家科技重大專項(2013ZX04002-082)；江蘇省科技支撐計劃資助項目(BE2012174)

TH112< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.01.006

李燁健，男，1987年生。南京理工大學機械工程學院博士研究生。主要研究方向為先進制造工藝及裝備。發表論文2篇。孫宇，男，1964年生。南京理工大學機械工程學院教授、博士研究生導師。胡峰峰，男，1988年生。南京理工大學機械工程學院博士研究生。