考慮非線性頻散效應的風浪關系及其應用
舒勰俊,侯 堋,江森匯
(1. 國家海洋局 南海海洋工程勘察與環境研究院,廣東 廣州 510300;2. 珠江水利科學研究院,廣東 廣州 510611;3. 中國科學院 南海海洋研究所,廣東 廣州 510301)
考慮非線性頻散效應的風浪關系及其應用
舒勰俊1,侯 堋2,江森匯3
(1. 國家海洋局 南海海洋工程勘察與環境研究院,廣東 廣州 510300;2. 珠江水利科學研究院,廣東 廣州 510611;3. 中國科學院 南海海洋研究所,廣東 廣州 510301)
隨著我國沿海地區海洋經濟的快速發展,相關海域的風浪規律的研究越來越受到人們的重視。依據Toba的風浪3/2指數律和非線性頻散關系推導得到一個新的波陡波齡關系式,簡化獲得適用于深水情況下的波陡波齡關系式;基于考慮非線性頻散效應的波齡波陡深水關系式,并結合有效波能量平衡方程,進一步推導出包含非線性頻散效應的深水海域風浪公式。利用新的深水風浪公式,并結合Mitsuyasu開闊海域風區、風速經驗公式,研究了江蘇沿海海域的風浪規律,且與NCEP再分析風浪數據以及其他公式結果進行對比分析。分析結果表明所獲得的新深水風浪公式適用范圍更廣,且在只考慮風速這個單一參數條件下計算得到的江蘇外海波浪要素與NCEP再分析風浪數據吻合程度最好,且更接近其他學者的研究成果。計算過程可避免開闊海域風區長度推算的不確定性和人為因素所產生的誤差,可為我國風浪成長規律的理論研究和海洋工程深海風浪要素推算提供參考。
波陡波齡關系;風浪關系;非線性頻散關系;江蘇外海
海浪是海洋中最顯著的自然現象之一,其生成及傳播等機制復雜,是影響泥沙輸運、污染物擴散等物理過程的重要動力因素之一,且對港口航道、防波堤以及海洋平臺等建筑物的選址、設計和建設具有決定性的影響。海浪研究中風浪成長關系是非常重要的,尤其是對于在開放外海的海洋工程,成長關系常常用來得到相關的波浪參數[1]。從物理角度而言,有效波能量平衡方程以整體的方式描述了由于風能輸入和破波耗散引起的風浪能量變化,因此有效波的概念常被用于從宏觀角度研究風浪成長[2],而此時需要波陡和波齡關系。
Sverdrup與Munk提出波陡波齡關系圖解方法以來,許多學者基于現場觀測和模型試驗得到各種波陡波齡關系式。Toba基于實驗室風浪水槽的觀測數據提出了著名的風浪指數律,在此過程中得到波陡波齡關系式[3],如表1所示。Neumann利用波面阻力概念研究風浪的能量傳遞,依據觀測數據提出了他的風浪波陡波齡關系式[4]。Крылов從風浪的三維性質出發,通過波浪的能量平衡方程推導得到平均波浪的波陡和波齡關系[4]。Ishida認為波陡波齡乘積為一個常數,根據觀測數據得到常數為0.027 6[5]。王炳祥將海浪情況作為海面粗糙度考慮,參照其他學者的波陡波齡關系式,同時根據大量深水和淺水波浪數據擬合得到波陡波齡關系公式[6]。根據許多學者的研究,海面粗糙度的范圍在0.5×10-3~4.0×10-3之間,Guan等[7]取平均值CD=2.25×10-3,代入Toba的指數律公式得到波陡波齡關系式。
以上波陡波齡公式中通過觀測數據或假設波浪滿足線性彌散關系,而更多情況下波浪更符合非線性彌散關系。因此文中主要根據Toba的風浪3/2指數律和非線性頻散關系推導出新的波陡波齡關系式,并聯合有效波能量平衡方程進一步推導得到適用深水情況下、且包含非線性頻散效應的風浪公式。基于獲得的新的風浪公式,并結合Mitsuyasu提出的開闊海域風區與風速經驗公式[8],推算江蘇外海的風浪要素。

表1 代表性的δ-β關系
注:波陡δ=H/L和波齡β=C/U;H,L,C和U分別為波高、波長、相速度和風速。
1 考慮非線性頻散效應的深水風浪成長公式推導
1.1考慮非線性頻散效應的波陡與波齡關系
由于特征波能量平衡方程從整體上描述了風能攝入和波能耗散導致的波動能量變化,目前特征波概念廣泛被用于研究風浪成長規律[9-10]。依據實驗數據Toba提出了著名的風浪3/2指數律[3],即在風的作用下,海浪的波高和波周期在統計意義上存在如下的關系
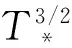
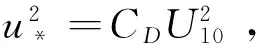
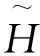
波陡δ和波齡β是研究風浪常用的物理量,基于能量變化的風浪成長理論在引入δ和β后,將問題轉化為如何找到一個δ和β的關系,以聯立求解風浪要素隨風要素的變化[6]。管長龍等[12]假定深水情況下有效波滿足線性頻散關系ω2=gk,并引入波陡和波齡,得到3/2指數律由波陡和波齡描述的表達形式
波浪線性彌散關系只在理想條件下才成立,在一定程度上并不適用于具有較強非線性的有效波,因此采用非線性彌散關系描述波浪的波陡和波齡關系更加符合實際波浪狀況。Li等[13-14]提出了一個適用于整個水深的非線性彌散關系,如式(4)所示。研究表明,式(4)對于波浪的刻畫相比較其他彌散關系更加準確。
式中:ω為角頻率,k為波數,h為水深,ε=ka,a為振幅。
在非線性彌散關系式(4)的基礎上,引入波陡δ和波齡β,得
在深水情況下式(5)化簡為
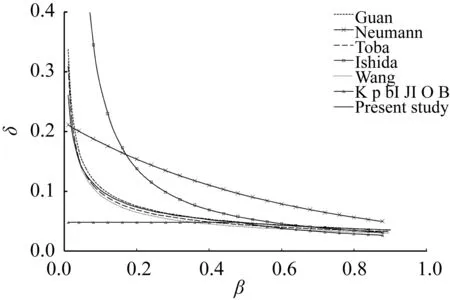
圖1 δ-β關系Fig. 1 δ-β relation of equations
由上式可以看出,式(3)為式(6)不考慮高階量O(δ4)時的簡化形式,說明式(6)在某些特定條件下可進一步簡化為式(3)。
參照管長龍等[2]的取值,當CD=2.25×10-3時所得δ-β關系與其他δ-β關系(見表1)如圖1所示。除了Neumann的δ-β關系式以及Крылов與其他人不同的特殊形式,這里所得δ-β關系式在β≤0.03范圍內的δ是較小的,且相比Neumann關系式,在β增加到0.05時,δ已經滿足Stokes波的波陡范圍0<δ<0.142,說明式(6)適用范圍更廣。從圖中可以看出,在β≤0.10時文中所得δ-β關系與Toba和王炳祥的公式更接近,當β>0.1時,隨著β的增加文中δ-β關系逐漸接近于管長龍的公式,這與δ逐漸接近于0是相對應的。
1.2考慮非線性頻散效應的風浪公式
以有效波代替實際波浪作為研究對象,于波動中選取一垂直水柱,水柱的斷面非常小,考慮波動作用整個區域,能量平衡方程為
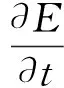
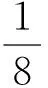
有效波滿足的Li非線性頻散關系公式在深水情況下化簡為
形式與二階Stokes波深水情況下的非線性頻散關系一致。于是有
引入波陡δ和波齡β,則
在定常風場條件下,將有效波運動視為二維的并取x軸與波向一致,則式(7)簡化為
將式(10)和式(11)代入式(12)有
式中:源項R包括風通過法向作用力和切向作用力傳遞給波動的能量以及分子粘性、渦動粘性、水底摩擦引起的波能耗散。由于分子粘性耗散的波能對于短波而言是重要的,對于長波的衰減影響非常小,只在小的風速和波齡情況下才能體現出它的影響,在平常的風速范圍內對于成長至一定程度的風浪可以忽略分子粘性的影響。深水情況下底摩阻導致的能量消減同樣可以忽略,因此,源項R只考慮通過法向作用力和切向作用力風能傳遞于波浪的能量以及渦動粘性引起的波能耗散[1]。
其中,
為遮攔系數,ρa是空氣的密度,κ為Karmann常數。

將式(6)、式(14)和式(15)代入式(13),最后得到波齡與無因次風區的關系式
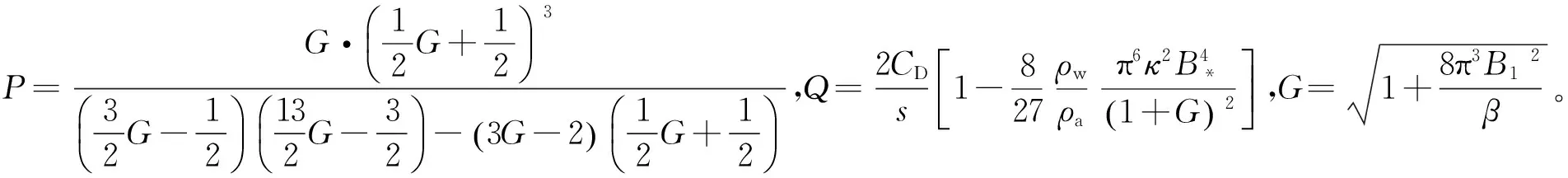
如圖2所示,由式(17)與式(16)得到的曲線非常吻合。
由式(6)和(17)可以得到
再由式(18)和(2)得到
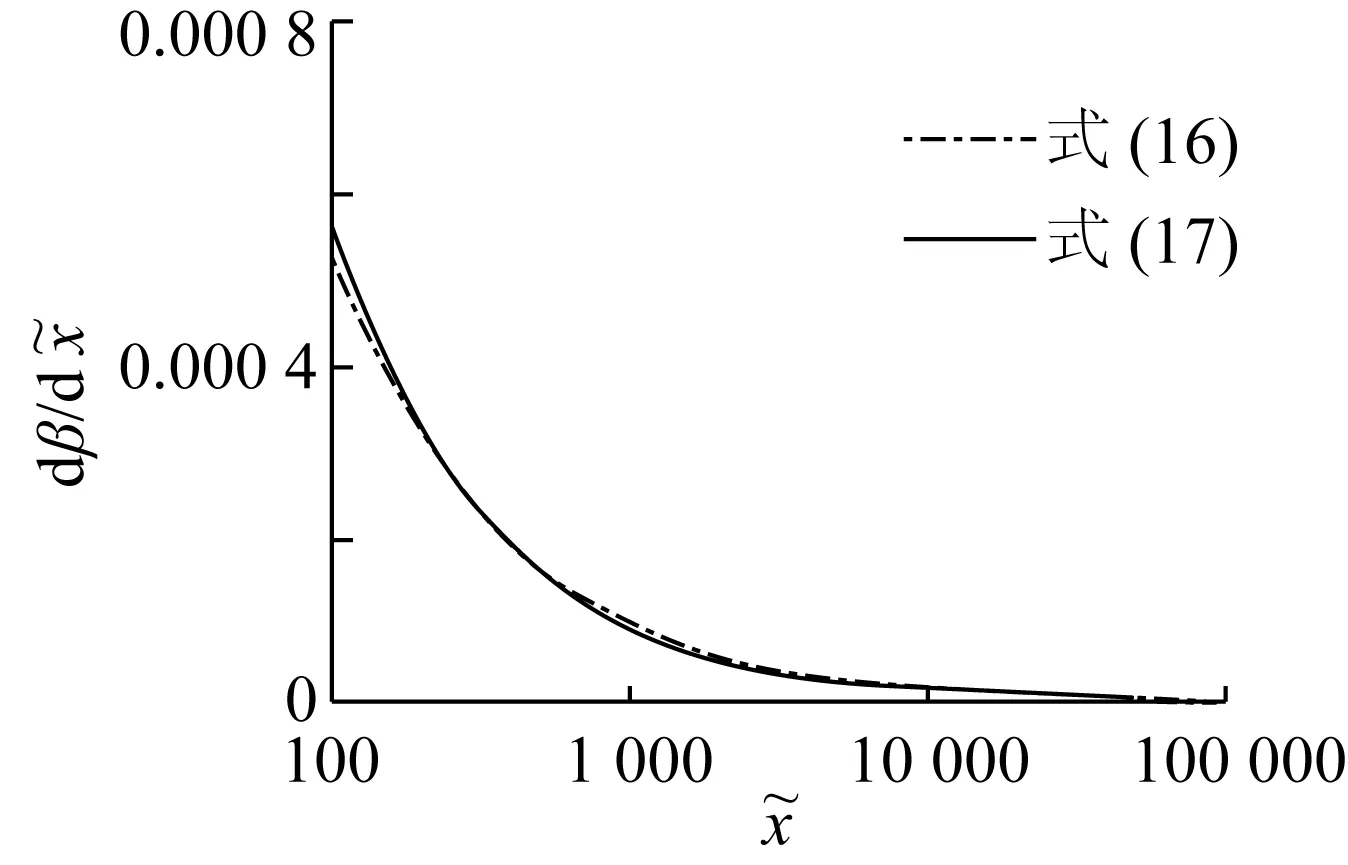
圖隨無因次風區變化關系Fig. 2 The relation between dβ/d and dimensionless fetch
2 在江蘇外海的應用及其比較分析
將推導出的新的風浪成長公式應用于江蘇外海海域波浪要素的計算,并與NECP再分析數據以及《海岸防護手冊》[15]、《海港水文規范》[16]和《堤防工程設計規范》[17]深水風浪公式進行比較分析。其中,NCEP再分析數據選取的時間為1997~2008年,選用的是坐標為(122.5°E,33°N)和(120°E,35°N),方向為NNE、NE、ENE、E、ESE和SE且波高大于0.5 m的波浪數據和相對應的風速數據,共計1 969組數據,如圖3和圖4所示。為了避免人為估算江蘇沿海沒有島嶼等遮擋的開闊海域風區長度的不確定性,Ff由Mitsuyasu風區經驗公式Ff=5×106/U10得到。
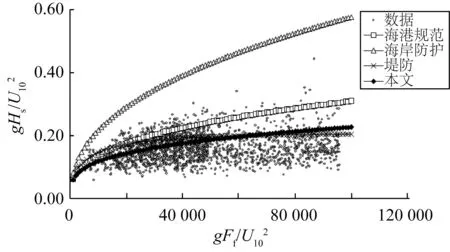
圖3 各公式關系 Fig. 3 The relationship between and of different equations

圖4 各公式關系 Fig. 4 The relationship between and of different equations
根據研究資料[18],江蘇海域25年一遇的風速U10為26.7 m/s,相應的外海有效波高為5.46 m。該風速條件下結合Mitsuyasu風區經驗公式,本文公式計算的有效波高為5.80 m,而其他公式的計算結果為5.91~6.36 m,本文公式可在只考慮風速一個參數的情況下計算的有效波高比規范公式更接近研究資料中江蘇外海波浪要素數值。
3 結 語
結合Toba的風浪3/2指數律公式和Li等提出的非線性頻散關系推導了一個新波陡波齡關系式并簡化得到其深水形式,基于考慮非線性頻散效應的波齡波陡深水關系式,并結合有效波能量平衡方程,進一步推導出適用于深水海域且包含非線性頻散效應的風浪公式,并將其運用到江蘇沿海海域的波浪要素推算,與NCEP再分析風浪數據以及其他公式結果進行對比分析。從結果可知考慮非線性頻散效應的波陡波齡關系的深水表示式趨勢與其他關系式相類似,但適用范圍擴大至非線性波浪。考慮非線性頻散效應的風浪關系在江蘇外海的計算結果與NECP再分析數據吻合程度最好,但從工程安全角度考慮《海岸防護手冊》公式安全性更高。另外,只考慮風速一個參數的情況下,本文風浪公式計算得到的江蘇外海波浪要素更接近其他學者的研究成果,同時可避免開闊海域風區長度推算中不確定性和人為因素所帶來的計算誤差。
[1] 文圣常,余宙文. 海浪理論與計算原理[M]. 北京:科學出版社,1984. (WEN Shengchang, YU Zhouwen. Ocean wave theory and computation principle [M]. Beijing: Science Press, 1984.(in Chinese))
[2] 管長龍,張淑芳,孫建,等. 深水風浪的風區指數律[J]. 中國海洋大學學報,2004,34(5):704-712. (GUAN Changlong, ZHANG Shufang, SUN Jian, et al. On the fetch law for wind waves in deep water [J]. Periodical of Ocean University of China, 2004, 34(5):704-712.(in Chinese))
[3] TOBA Y. Local balance in the air-sea boundary processes I. On the growth process of wind wave [J]. J. Oceanogr. Soc. Japan, 1972, 28: 109-121.
[4] 文圣常. 海浪原理[M]. 濟南:山東人民出版社,1962. (WEN Shengchang. Wave principle [M]. Jinan: Shandong People Press, 1962.(in Chinese))
[5] ISHIDA. Stocks波の境界層特性に關する風洞ならぴに水槽實驗[J]. 海と空,1967,42(3、4):23-49. (ISHIDA. The experiments of wind tunnel and flume about boundary layer characteristics of Stocks wave [J]. Ocean and Atmosphere, 1967, 42(3、4):23-49. (in Japanese))
[6] 汪炳祥. 海浪的δ-β關系的探討[J]. 青島海洋大學學報, 1990, 20(3): 1-10. (WANG Bingxiang. An investigation on the δ-β relationship of ocean waves [J]. Journal of Ocean University of Qingdao, 1990, 20(3):1-10.(in Chinese))
[7] GUAN Changlong,SUN Qun. Analytically derived wind wave growth relations [J]. China Ocean Engineering,2002, 16(3):359-368.
[8] MITSUYASU H. On the growth of the spectrum of wind-generated waves (1) [J]. Rep. Res. Inst. Appl. Mech. Kyushu Univ., 1968, 16(55):459-482.
[9] 高山,孫孚. 風浪場波生橫向徹體切應力的分析[J]. 海洋與湖沼,2005,36(4):367-375. (GAO Shan, SUN Fu. Analysis of wave-induced lateral body force [J]. Oceanologia Et Limnologia Sinica, 2005, 36(4): 367-375. (in Chinese))
[10] 舒勰俊,江森匯. 國際近海工程研究進展——第26屆近海力學與極地工程國際會議海洋工程分會簡介[J]. 海洋工程, 2009, 27(1): 110-114.(SHU Xiejun, JIANG Senhui. An introduction of 26th international conference on offshore mechanics and arctic engineering [J]. The Ocean Engineering, 2009, 27(1): 110-114. (in Chinese))
[11] EBUCHI N,TOBA Y,KAWARMURA H. Statistical study on the local equilibrium between wind and wind waves by using data from ocean data buoy stations [J]. J. Oceanogr,1992,48:77-92.
[12] 管長龍,孫群. 風浪成長關系的分析及其對3/2指數律的支持[J]. 青島海洋大學學報,2001,31(5):633-639.(GUAN Changlong, SUN Qun. Analysis of wind wave growth relations and their support to the 3/2 power law [J]. Journal of Ocean University of Qingdao, 2001, 31(5):633-639.(in Chinese))
[13] LI Ruijie,YAN Yixin, CAO Hongsheng. Nonlinear dispersion relation in wave transformation [J]. China Ocean Engineering,2003,17(1):117-122.
[14] LI Ruijie, TAO jianfu. Analysis of wave nonlinear dispersion relations[J]. China Ocean Engineering, 2005, 19(1):167-174.
[15] Coastal Engineering Research Center, U. S. Army. Corps of engineers shore protection manual [S]. Vicksburg. M S,1984.
[16] JTS145-2-2013,海港水文規范[S].北京:人民交通出版社,2013. (JTS145-2-2013,Code of hydrology for sea harbor [S]. Beijing: China Communications Press, 2013.(in Chinese))
[17] GB50286-2013,堤防工程設計規范[S]. 北京:中國計劃出版社,2013. (GB50286-2013,Code for design of levee project[S]. Beijing: China Plan Press, 2013.(in Chinese))
[18] 黃穎. 黃海陸架輻射沙脊群[M]. 北京:中國環境科學出版社,2002. (HUANG Ying. Radial sandy ridge of the Yellow Sea continental [M]. Beijing: China Environmental Science Press, 2002.(in Chinese)
Research on wind wave considering nonlinear dispersion effect and its application
SHU Xiejun1, HOU Peng2, JIANG Senhui3
(1. South China Sea Marine Engineering and Environment Institute, State Oceanic Administration, Guangzhou 510300, China;2. Scientific Research Institute of Pearl River Water Resources Commission,Guangzhou 510611, China;3. South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China)
With the rapid economic development of China’s coastal waters, wind wave mechanism is more and more concerned. This paper primarily introduces the deduction of new wind wave growth relations. Firstly, a new relation formula between wave steepness and wave age was deduced by combining the 3/2 power law developed by Toba with the nonlinear dispersion relation deduced by Li et al., and by ignoring the effect of water depth. Secondly, based on the combination of this new relation formula with the significant wave energy balance equation, new wind wave growth relation formulae including the wave nonlinear dispersion effect of wave amplitude were deduced. When the deduced growth relation formulae were applied in the offshore area of Jiangsu considering Mitsuyasu’s empirical formula for the open sea fetch and wind speed, accurate open sea wave parameters of Jiangsu could be formulated by only considering one parameter, such as wind speed. Overall, as this methodology can avoid the uncertainty about the fetch of open sea and operation error during the calculation process, results gained from this report have higher accuracy than other published formulae. The results were validated by NCEP reanalyzed data of the open sea of Jiangsu and other researches. The new relations provide references for studying wind wave growth theory and calculating open sea wave parameters of ocean engineering.
relation between wave steepness and wave age; wind wave relations; nonlinear dispersion effect; open sea of Jiangsu
TV139.2
A
10.16483/j.issn.1005-9865.2015.01.010
1005-9865(2015)01-0083-07
2014-04-14
國家海洋局南海分局海洋科學技術局長基金資助(1407)
舒勰俊(1983-),男,江西靖安人,工程師,主要從事海洋動力及環境的研究。E-mail:shuxj@scsb.gov.cn
江森匯(1983-),男,浙江玉環人,助理研究員,主要從事物理海洋學的研究。E-mail: jiangsenhui@scsio.ac.cn

