基于近場聲全息的水下航行器噪聲源定位方法

姬　慶，蔣　培，孫玉繪

（海軍工程大學 兵器工程系，湖北 武漢，430033）

基于近場聲全息的水下航行器噪聲源定位方法

姬慶，蔣培，孫玉繪

（海軍工程大學 兵器工程系，湖北 武漢，430033）

以水下航行器的噪聲源定位為研究背景，綜合論述了基于空間傅里葉變換的近場聲全息技術的研究現狀，重點研究了算法誤差、重建穩定性和濾波方法，分析了近場聲全息技術目前仍需解決的問題，并結合Patch近場聲全息、矢量水聽器等新技術給出了相應的建議，旨在為近場聲全息應用到水下噪聲源定位提供依據。

水下航行器； 噪聲源定位； 近場聲全息（NAH）； 濾波

0　引言

水下航行器是重要的工業技術集合體，但較大的輻射噪聲可能會暴露其在布放、攻擊過程中的位置信息，或使敵方在遠距離外予以規避并進行反擊。準確地對水下航行器的噪聲源進行定位是對其輻射噪聲特性研究，提高聲隱身性，攻擊命中率的前提，也是利用現代聲學診斷進行故障診斷的關鍵技術。

20世紀80年代，近場聲全息（near-field acoustic holography，NAH）的提出為可視化空間聲場和定位噪聲源提供了一種強力工具，該技術一經提出立刻成了各國學者研究的熱點。隨著NAH技術理論的日趨成熟，NAH技術已應用到聲源或振動體的測量與分析、噪聲識別與定位、聲場可視化等方面［1-3］。將NAH技術應用于水下航行器的噪聲源定位，有著重要的軍事經濟效益。文中概括了基于空間傅里葉變換（spatial Fourier transform，SFT）的NAH技術發展和現狀，提出了該技術現存問題和發展展望，旨在探討NAH應用到水下航行器目標的聲源定位識別研究中。

1　SFT-based NAH基本原理

NAH技術相對于傳統聲全息技術和遠場聲全息技術而言，突破了由于測量距離遠、無法記錄“倏逝波”成分導致的重構分辨率不超過λ/2和不適宜與高分辨率場合的限制，所以在對目標聲源定位及高精度聲場重建方面有明顯優勢［4］。聲場變換算法是NAH的核心，是聯系全息面和重建面的紐帶。相比其他聲全息技術［5-7］，SFT-based NAH是最早提出、理論最為成熟、應用也最為廣泛的一種NAH技術，原理示意見圖1。

SFT-based NAH是基于亥姆霍茲-基爾霍夫公式和2D 傅里葉變換的方法。基本思想是全息面上的聲壓可以表示成源面上的聲壓和在源面上滿足Dirichlet邊界條件的格林函數的卷積，聲場重建過程即為卷積的解卷過程。借助于傅里葉變換技術可以實現從全息面到源面的聲場重建。由于實現時常借助于快速傅里葉變換（fast Fourier transform，FFT）快速計算，所以也稱為FFT- based NAH。平面NAH理論是基于空間傅里葉變換聲全息技術的理論基礎，現就平面NAH理論來闡述NAH基本原理，實現原理如圖2所示。

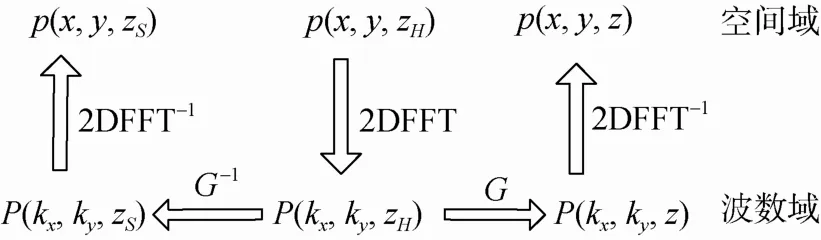
圖2　平面近場聲全息算法實現原理Fig. 2　Implementation principle of planar NAH algorithm

根據理想流體媒質中小振幅聲波的波動方程，可以得到不依賴于時間變量的穩態聲場的Helmholtz方程

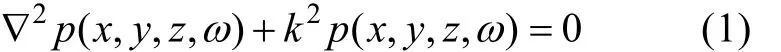
式中： p（x，y，z，ω）為空間點的復聲壓； k為波數，且k=ω/c=2π/λ； ω為角頻率； c為聲速。

在Dirichlet邊界條件下，對于z＞zH≥0的正向聲場，重建面上的復聲壓是由全息平面測得復聲壓和格林函數的卷積積分求得，即

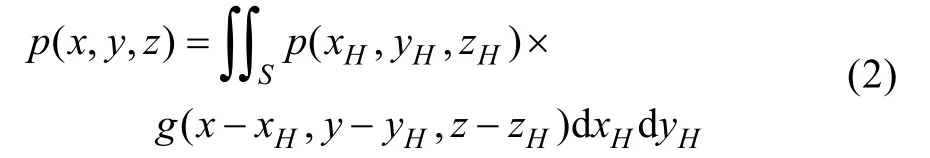
式中： S表示無窮大邊界的積分平面； g為無窮大平面上的格林函數； p（x，y，z），p（xH，yH，zH）分別為重建面和全息面聲壓。

若定義空間內沿x，y方向的2D連續傅里葉變換為

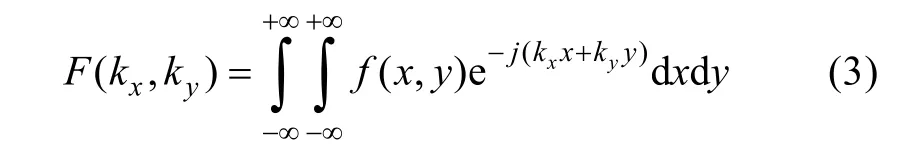
式（2）兩邊做2D 傅里葉變換，并由2D卷積定理得

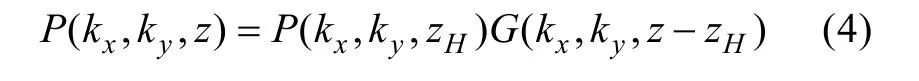
式中：P（kx，ky，z），P（kx，ky，zH），G（kx，ky，z-zH）分別為p（x，y，z），p（xH，yH，zH），g（x-xH，y-yH，z-zH）的2D 傅里葉變換。

變換域的坐標對應關系為（x，y）?（kx，ky），且kx，ky分別為x，y方向的波數分量。對式（4）進行傅里葉逆變換即可求得重構面聲壓分布

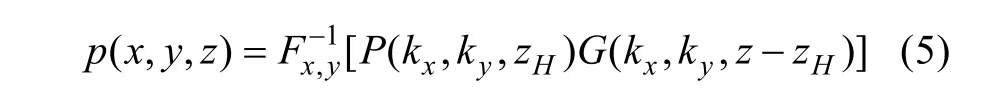
當重構平面位于源平面和全息平面之間時，即當zS≤z≤zH，定義逆向傳遞因子G-1（kx，ky，zH-z）］=Fx，y［g（x-xH，y-yH，z-zH）］，則逆向重建聲壓為

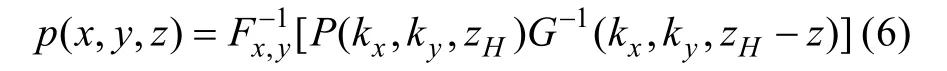
繼而可求解聲場聲速、聲強等聲學參量，完成對聲場的重建。也可以在Neumann邊界條件下以聲源表面振速為輸入量，依據NAH基本原理對聲場進行重建。

2　正交共形結構近場聲全息

為解決早期全息技術分辨率受限的問題，在20世紀70年代末，Skudrzyk等就開始了有關SFT-based NAH研究［8］。直到1980年，E. G. Williams等人完整地闡述了基于2D空間傅里葉變換及其逆變換方法實現聲場重建的NAH理論［9］。隨后E. G. Williams等利用NAH技術研究了自由聲場中平板聲源的振動和聲場輻射，并在空氣和水中進行了試驗研究［10-11］。

NAH技術提出后，在噪聲源識別領域吸引了眾多學者的關注并開展廣泛的研究。此后的30年，許多學者對NAH技術展開深入研究，在NAH的理論基礎、物理過程、數值實現方法、誤差分析以及拓展噪聲源識別應用方面取得了豐碩的研究成果。

1987年，E. G. Williams等率先利用漢克爾函數將NAH推廣到柱坐標系近場聲全息（cylindrical NAH，CNAH）［12］。CNAH技術關鍵是將柱狀或類柱狀聲源輻射的聲波在柱面波函數上分解，并給出全息變換的數學表達和物理解釋。在柱面坐標系下，可建立重建面與全息面之間的波譜關系為

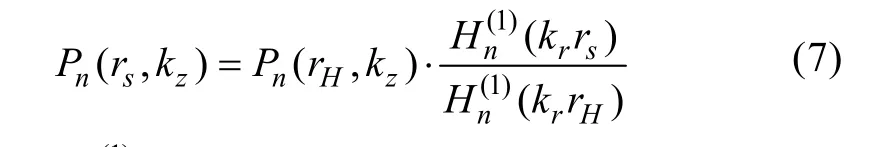
對式（7）傅里葉逆變換即可實現了從全息面到源面的聲壓場重建。由歐拉公式，也可以重建面上的法向振速vn（rs，φ，z）。隨后Williams等人將CNAH應用于重建點激勵振動有限長圓柱附近的聲強分布，由于NAH技術不受梯度近似誤差的影響，重建結果明顯優于雙水聽器直接測得的聲強分布。到了1990年，A. Sarkissian又提出了軸對稱聲全息技術，用以分析軸對稱聲源［13］。

1996年，J. C. Lee等利用貝塞爾函數（Bessel）又將NAH推廣到球坐標系下的聲全息聲場轉換（spherical NAH，SNAH），利用數值仿真和冰箱壓縮機試驗都表明SNAH能夠精確定位噪聲源［14］。在球坐標系中，根據Helmholtz方程一般解的形式可得球面空間聲場的全息變換

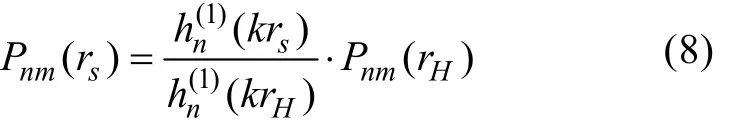
對式（8）進行傅里葉逆變換即得半徑為rs的球面上的空域聲壓p（rs，θ，φ）。SNAH實現算法與以上2種NAH不同之處在于不能借助FFT進行計算。

至此，SFT-based NAH基本理論完全建立。由于傅氏變換的本征函數是正交函數系，因此理論上有多少種正交坐標系和相應的正交函數組就可以建立相應的正交共形結構聲場轉換關系［15］。由于SFT-based NAH技術要求聲源結構與全息面形狀相同，故又稱為正交共形NAH。隨著NAH研究的不斷深入，隨后衍生了基于聲強測量的寬帶近場聲全息技術（broadband acoustic holography based on intensity measurement，BAHIM）、移動框架聲全息技術（moving frame acoustic holography，MFAH）等技術。使基于Fourier變換的NAH技術的應用范圍不斷擴大，從單頻穩態聲場逐漸擴展到了寬帶聲源聲場、移動聲源聲場、多源聲場和瞬態聲場。隨后，NAH技術的研究重點轉向了改善全息重建穩定性，提高重建精度，減小重建誤差上。

3　算法誤差及濾波方法

3.1近場聲全息技術算法誤差分析

NAH技術的算法誤差主要有4種： 有限孔徑效應、卷繞誤差、測量誤差及逆向重建的不穩定性。實際進行聲壓測量時，全息數據為有限全息孔徑上離散空間點的聲壓幅值。因為有限測量孔徑產生的誤差稱為有限孔徑效應，也稱“窗效應”。離散處理使空間連續的聲壓分布抽樣成離散點上的聲壓。本質上，相當于對所研究的實空間聲壓信號進行了加窗處理和離散處理。

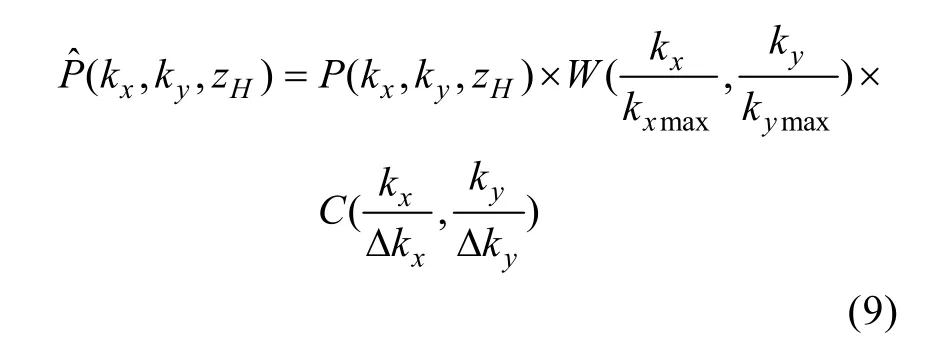
理論上，加窗會造成連續信號截斷產生頻譜泄露誤差、邊緣的吉布斯效應。由于2D離散傅里葉變換的周期延拓性，使參與運算的波數域聲壓序列由主值序列和無窮多個“虛像”組成。這些虛像也將“卷繞”回全息孔徑與傳遞函數作卷積。因此產生的誤差稱為“卷繞誤差”，也稱孔徑重復效應，這2種是SFT-based NAH不可消除的誤差。

除了對重構算法誤差進行分析改進，K. U. Nam，Y. H. Kim［16］和G. P. Garroll等人［17］對背景噪聲、測量面位置偏差、傳感器位置偏差和傳感器間的響應一致性偏差等產生的NAH重建誤差也進行了系統分析，給出了隨機誤差與測量參數間的定量關系式，對NAH試驗具有參考作用。

利用NAH進行聲場逆向定位屬于聲學逆問題，逆向傳遞函數G-1成指數性增大，致使聲場中高波數成分、測量誤差及其他噪聲隨著逆向重構急劇增大，這就是逆向重構的不穩定，進行聲源逆向定位時必須予以解決。

3.2濾波方法

為減小NAH技術重建誤差，提高重建精度。1985年，J. D. Maynard等研究了有限全息孔徑帶來的誤差問題，比如聲源表面振速重建時的卷繞誤差等，提出可以通過對全息面補零形成“保護帶”，來降低卷繞誤差［10］。

NAH在解決聲場輻射逆問題時，具有很強的不穩定性。較小測量誤差或離散化誤差在逆向重建過程中都可能會被G-1因子無限放大。目前主要解決辦法是空間域和波數域濾波處理。V. A. Veronesi等提出的波數域濾波法，主要討論如何選取截止波數kc問題［18］。1986年，Fleischer提出了一種波數域的維納濾波

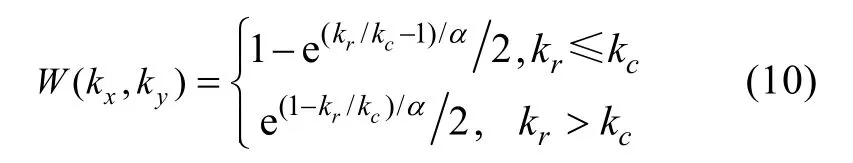
該函數主要參數為信噪比，形式簡單，得到了廣泛應用。但在測量面離源面較近時有效，隨距離增大，效果變差［19］。1995年，M. R. Bai修改了一般的維納濾波窗函數，給出1種波數域濾波迭代算法［20］，取得了很好的全息重建效果。

E. G. Williams和J. Hald分別提出具有聲壓和質點振速約束的迭代窗函數［11，21］，分別適用于無障板和有障板的平面聲源，但是二者的計算量都比較大。1995年，H. S. Kwon和Y. H. Kim通過對窗函數帶來的偏差進行Taylor級數展開，推導出一種最小誤差窗函數，并將其重建結果同Hanning窗、Gaussian窗等傳統窗函數的處理結果進行了對比［22］。

中科院武漢物理所張德俊提出一種需要測量先驗知識的空間頻域濾波函數： 帶約束條件的最小二乘濾波函數

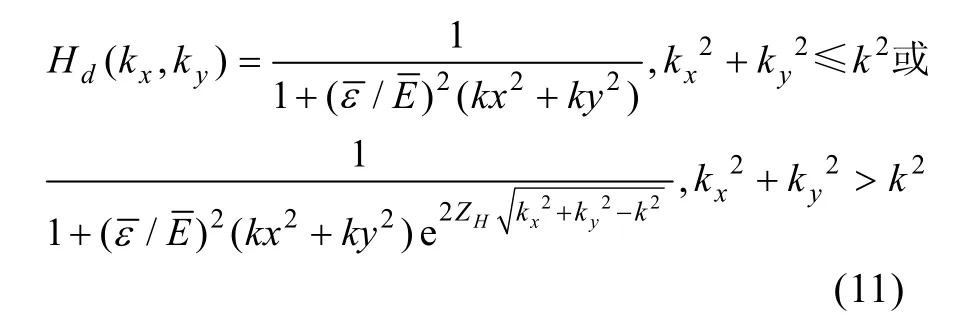
該濾波函數在一定程度上改善了重建結果的穩定性，但是在高、低邊帶上的光滑性差，同時這種先驗知識一般不易獲得［23］。后來J. F. Li等通過改變約束條件，提出改進的最小二乘濾波函數，改善了窗函數在高、低邊帶的光滑性［24］。2000年，何元安和何祚鏞等提出聯合迭代濾波窗即結合Hald的振速約束迭代窗與J. F. Li的波數域窗2種方法，進一步改善了重建效果。

此外，J. H. Thomas和J. C. Pascal等將小波分析理論引入NAH的重建過程［25］，解決由于重建不穩定性帶來的聲源邊界產生的吉布斯現象，實質上該方法也相當于一種窗函數濾波。

近年來，正則化的概念被引入基于傅里葉變換的NAH技術，提出Tikhonov、共軛梯度等4種健全的正則化方法，以及偏差原理等2種正則化參數選取方法，這些方法對解決聲場逆向重建穩定性提供了新的方向［26］。國內對NAH技術研究時間較短，但也取得豐碩的成果，陳曉東、馬佳楠等對重建過程格林函數誤差進行了詳盡分析；哈爾濱工程大學、武漢物理研究所及上海交通大學等單位對NAH技術也都有深入的研究［2，15，23］。

4　存在問題與發展趨勢

基于傅里葉變換的NAH技術一經提出就受到廣泛關注，并得到長足發展，是目前理論最成熟、計算速度最快、應用廣泛的1種NAH技術。但FFT-based NAH仍有一些需進一步研究的課題。

4.1算法的適用性問題

SFT-based的NAH技術由于需借助于傅里葉變換，因此算法只能適應于規則聲源結構的聲場研究中。雖然可以借助于FFT減小計算量提高計算效率，但是聲源結構的適用性一直制約著SFT-based NAH技術無法得到廣泛的實際應用。基于BEM（boundary element method）的NAH、基于ESM（equivalent source method）的NAH雖然可以實用于任意形狀的聲源結構，但計算量大、效率不高。如何改進現有的算法或提出1種新的適用性強且計算效率高的NAH算法是NAH技術一個重要研究方向。

4.2全息面數據的獲取

如何高精度、高效率的獲取足夠大的全息面數據是決定聲場重建的前提。“有限全息孔徑”一直是影響全息重建精度和逆向重建穩定性的制約因素； 快速測量對于非穩態聲場尤為重要； 如何獲取高質量的全息數據，尤其是針對水下航行器目標的水聲測量，一直是實際應用的關鍵因素。現代測試技術和陣列信號處理技術快速發展，為解決快速測量和小采樣間隔提供了有力的技術支持。結合Patch NAH可以實現局部聲場測量和局部聲場重建，也為解決有限全息孔徑問題提供了思路。所以結合陣列信號處理和Patch NAH是實現獲取高質量全息數據的有效解決方向。

4.3基于質點振速的NAH

在NAH算法中，基于聲壓量和聲強量的重建分析較普遍，隨著矢量水聽器的發展，振速越來越受到學者的關注。作為振動體輻射的結果量，質點振速包含了與復聲壓一樣的聲場信息。隨著矢量水聽器、指點振速傳感器的技術發展，使得基于振速的NAH成為可能。因此如何利用振速信息，以及利用聲壓和振速信息的關聯和差別實現更多的工程應用，成為目前值得研究的問題。

5　結束語

由于NAH技術能夠利用聲場中的“倏逝波”成分，能夠獲得高分辨、高精度的聲場重建結果，在水下航行器的噪聲源定位研究中有明顯技術優勢。而且NAH技術采用“貼近”測量，可實現在相對小空間的生產現場、維修泊位進行檢測與分析，從而完成對水下目標主要噪聲源的定位，為減振降噪、低噪聲設計提供理論支撐。

重點對基于空間Fourier的NAH技術進行研究。總結了基于空間聲場變換的NAH發展歷程，重點對NAH技術的誤差分析和重建穩定性進行研究。對NAH技術中仍需解決的問題進行了分析，并給出了相應的建議。這些問題的深入解決將使NAH技術在水下航行器裝備水下目標的噪聲源定位研究中獲得更為廣泛的應用。

［1］旸高. 近場聲全息技術簡介［J］. 現代物理知識，2007，19（5）： 39-42.

［2］陳心昭，畢傳興，張永斌. 近場聲全息技術及其應用［M］. 北京： 科學出版社，2013.

［3］王群. 全息技術及其軍事應用［N］. 中國國防報，2013，12（7）： 1-3.

［4］希爾德布蘭德BP. 聲全息導論［M］. 北京： 科學出版社，1978： 79-85.

［5］Veronesi W，Maynard J. Digital Holographic Reconstruction of Sources with Arbitrarily Shaped Surfaces［J］. Journal of the Acoustical Society of America，1989，85（2）：588-598.

［6］于飛，陳劍，李衛兵，等. 一種穩健的全波數空間聲場重構技術［J］. 中國科學（E輯），2004，34（9）： 1069-1080.

［7］Williams E G. Continuation of Acoustic Near-fields［J］. Acoustical Society of America，2000，113（3）： 1273-1281.

［8］Williams E G. The Beginnings of Near-field Acoustic Holograph Under Eugen Skudrzyk［J］. Acoustical Society of America，1992，91（4）： 2335-2339.

［9］Williams E G，Maynary J D，Skudrzyk E. Sound Source Reconstructions Using a Microphone Array［J］. Acoustical Society of America，1980，68（1）： 340-344.

［10］Maynard J D，Williams E G，Lee Y. Near-field Acoustic Holograph： Theory of Generalized Holography and the Development of NAH［J］. Acoustical Society of America，1985，78（4）： 1395-1413.

［11］Williams E G，Dardy H D. Near Field Acoustical Holography Using an Underwater Automated Scanner［J］. Acoustical Society of America，1985，78（2）： 789-798.

［12］Willams E G，Dardy H D. Generalized Near Field Acoustical Holography for Cylindrical Geometry： Theory and Experiment［J］. Acoustical Society of America，1987，81（2）： 389-407.

［13］Sarkissian A. Near-field Acoustic Holography for an Axis-symmetric Geometry： A New Formulation［J］. Acoustical Society of America，1990，88（3）： 961-966.

［14］Lee J C. Spherical Acoustical Holography of Lowfrequency Noise Sources［J］. Applied Acoustics，1996，48（1）： 85-95.

［15］蔣偉康，萬泉. 近場聲全息理論與應用的研究現狀與展望［J］. 機械強度，2005，27（3）： 288-295.

Jiang Wei-kang，Wan Quan. Review and Outlook of Researches on Near Field Acoustical Holography Theories with Application［J］. Journal of Mechanical，2005，27（3）：288-295.

［16］Nam K U，Kim Y H. Errors Due to Sensor and Position Mismatch in Planar Acoustic Holography［J］. Acoustical Society of America，1999，106（4）： 1655-1665.

［17］Carroll G P. The Effect of Sensor Placement Error on Cylindrical Near-field Acoustic Holography［J］. Acoustical Society of America，1999，105（4）： 2269-2276.

［18］Veronesi W A，Maynard J D. Near-field Acoustic Holography（NAH）II. Holographic Reconstruction Algorithms and Computer Implementation［J］. Acoustical Society of America，1987，81（5）： 1307-1322.

［19］Fleischer H，Axelrad U. Restoring an Acoustic Source from Pressure Data Using Wiener Filtering［J］. Acoustical Society of America，1986，60（2）： 172-175.

［20］Bai M R. Acoustical Source Characterization by Using Recursive Wiener Filtering［J］. Acoustical Society of America，1995（97）： 2657-2663.

［21］Hald J. Reduction of Spatial Windowing Effects in Acoustic Holography［C］//Noise-Con9. Yoko-Hama（Japan），1994： 1887-1890.

［22］Kwon H S，Kim Y H. Minimization of Bias Error Due to Windows in Planar Acoustic Holography Using a Minimum Error Window［J］. Acoustical Society of America，1995，98（4）： 2104-2111.

［23］張德俊. 近場聲全息對振動體及輻射場的成像［J］. 物理學進展，1996，16（3）： 613-623.

Zhang De-Jun. Imaging for Vibration Mode and Radiation Field of Vibration Object Using NAH［J］. Progress in Physics，1996，16（3）： 613-623.

［24］Li J F，Pascal J C，Carles C. A New k-space Optimal Filter for Acoustic Holography［C］//Canada： Proceedings of 3rd International Congress on Air and Structure-Borne Sound and Vibration，1994： 1059-1066.

［25］Thomas J H，Pascal J C. Using Wavelet to Reduce Distortion Problems in Near-field Acoustic Holography［C］//Hague Netherlands： Interntional Congress on Noise Control Engineering 2001，2001.

［26］Williams E G. Regularization Methods for Near-field Acoustical Holography［J］. Journal of the acoustical society of America，2001，110（4）： 1976-1988.

（責任編輯： 楊力軍）

Noise Source Location Method Based on Near-field Acoustic Holography for Underwater Vehicles

JI Qing，JIANG Pei，SUN Yu-hui
（Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，China）

In regard to the localization of noise source for underwater vehicles，such as torpedoes and mines，the current studies on the near-field acoustic holography（NAH）based on spatial Fourier transform are discussed with emphasis on algorithms′ reconstruction error，reconstruction stability and filtering methods. The problem in NAH technology，which still needs to be solved，is analyzed. Further，corresponding suggestions about applying such new technologies as Patch NAH and vector hydrophone to location of underwater noise source are offered.

underwater vehicles； sound source location； near-field acoustic holography； filtering

JT630.34； TM525

A

1673-1948（2015）01-0020-06

2014-10-10；

2014-11-18.

姬慶（1991-），男，在讀碩士，研究方向為軍用目標特性及信息感知技術.