基于MATLAB的魚雷推進軸系彎曲振動渦動頻率計算

趙　琪，尹韶平，王　中，郭　君

（1. 中國船舶重工集團公司 第705研究所，陜西 西安，710075； 2. 水下信息與控制重點實驗室，陜西 西安，710075）

基于MATLAB的魚雷推進軸系彎曲振動渦動頻率計算

趙琪1，2，尹韶平1，2，王中1，2，郭君1

（1. 中國船舶重工集團公司 第705研究所，陜西 西安，710075； 2. 水下信息與控制重點實驗室，陜西 西安，710075）

在魚雷轉子系統中，為避免系統發生共振，常需要計算其渦動頻率。鑒于商業有限元分析軟件的輸入參數有限，且無法滿足特殊情況下的計算需求，該文根據轉子系統的運動微分方程及其求解過程，運用MATLAB軟件編程來計算系統的渦動頻率，然后與ANSYS軟件計算結果進行對比。結果表明，所編寫的MATLAB程序合理，可對魚雷推進軸系進行計算，也可進行后續開發。

魚雷推進軸系； 彎曲振動； 渦動頻率

0　引言

一般工業中常見的機器都裝有旋轉部件即轉子。 轉子連同它的軸承和支座等統稱為轉子系統。轉子系統的振動是多樣的，包括轉軸的縱向振動、扭轉振動和彎曲振動等。其中轉軸的彎曲振動較為復雜，牽扯的因素較多。該文就是以轉軸的彎曲振動作為研究對象。

求解系統的渦動頻率及臨界轉速，是轉子動力學研究的重要內容之一［1］。當轉子達到臨界轉速時，往往產生劇烈振動，為了避免這種現象，就必須計算轉子的渦動速度。計算方法有傳遞矩陣法和有限元法等。采用有限元法建立的模型能考慮的因素比傳遞矩陣多，且數值穩定，計算精度較高，因此得到了非常廣泛的應用。現在應用較多的有限元分析軟件，如ANSYS，ABAQUS等，雖然都可以進行軸系振動特性分析，但其輸入參數有限（如彈簧的剛度阻尼系數等），而實際情況又都較為復雜，存在彎、扭、縱的耦合振動，需要考慮更加全面的邊界條件； 另一方面，當商業軟件不能滿足特定情況的計算需求時，要對其進行更多功能的開發較為困難。因此該文采用MATLAB編程計算和分析，實現對輸入參數的控制，也為后續其他功能的實現打好基礎。

1　有限元分析理論基礎

1.1渦動頻率

通常轉軸的兩支點在同一水平線上，中心線是水平的。當圓盤受橫向力作用，圓盤或轉軸的中心o′在互相垂直的2個方向作頻率同為wn的簡諧運動。一般情況下，中心o′的軌跡為一橢圓，如圖1所示。o′的這種運動是一種“渦動”或稱“進動”，自然頻率wn稱為渦動角速度［2］。

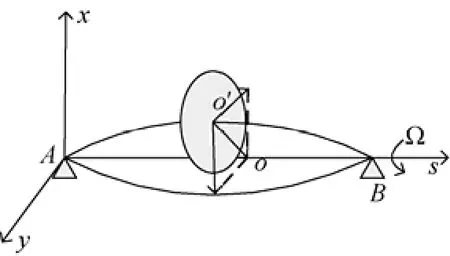
圖1　轉子渦動示意圖Fig. 1　Schematic of rotor whirling

1.2運動微分方程

轉子系統通常由剛性圓盤、彈性軸段和軸承座等部件組成，因此可沿軸線將轉子系統劃分為圓盤、軸段和軸承座等單元，各單元間彼此在結點處聯結。結點通常選在圓盤中心、軸頸中心以及軸的變截面等位置。如以軸承座中心線為s軸建立坐標，則轉子系統的具體結構見圖2［3］。

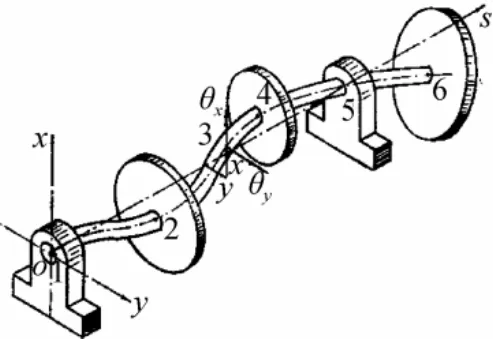
圖2　轉子系統結構Fig. 2 Structure of a rotor system

基于上述模型，建立轉子系統運動微分方程

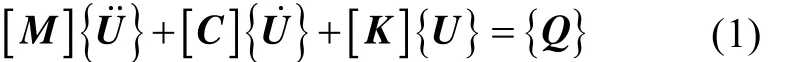
式中： ｛U｝，｛Q｝分別為系統位移向量及廣義力；［M］，［C］和［K］分別為系統質量矩陣、回轉矩陣和剛度矩陣。系統矩陣是由單元矩陣根據對應結點疊加而成的。

1.3結點為4自由度的單元矩陣形式

若考慮每個結點為4自由度狀態，則任一截面的位移可表示為

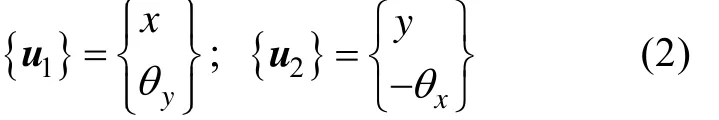
設剛性圓盤的質量、直徑轉動慣量和極轉動慣量分別為m，Jd和Jp，則圓盤的質量矩陣［Md］和回轉矩陣［Gd］為

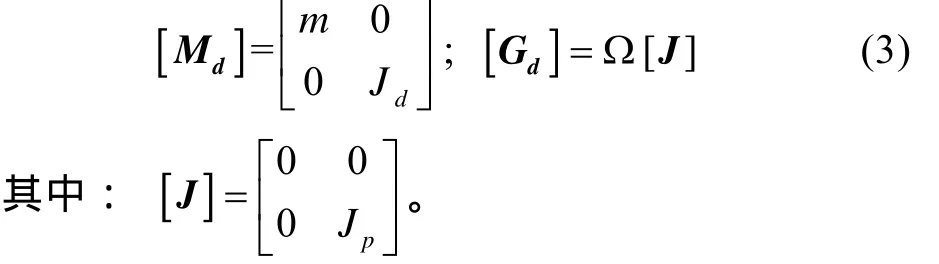
設軸段單元長度為l，半徑為r，單位長度質量為μ。則其移動慣性矩陣［MsT］、轉動慣性矩陣［MsR］和回轉矩陣［Gs］分別為［4-5］

可得軸段單元的質量矩陣為

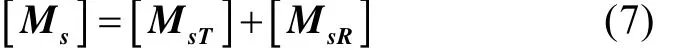
軸段單元剛度矩陣為

根據各單元間的相互作用關系，將單元矩陣進行集總，形成系統整體矩陣。

1.4結點為6自由度的單元矩陣形式

若考慮每個結點為6自由度狀態，圓盤單元只有一個結點，其位移向量可表示為

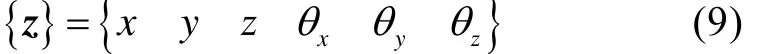
其質量矩陣及回轉矩陣可表示為

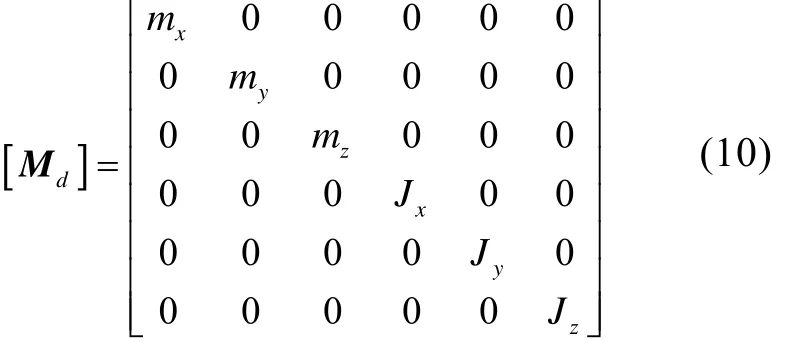
其中： mx，my和mz為質量單元3個方向的質量； Jx為極轉動慣量； Jy，Jz為直徑轉動慣量。

軸段單元為兩結點單元，每個結點均有6個自由度，其單元的剛度矩陣為［6］

式中： A為橫截面面積； Ixx是橫截面對x軸的極慣性矩； Iyy和Izz是單元截面對y和z軸的主慣性矩。

軸段單元的一致質量矩陣為［7-8］

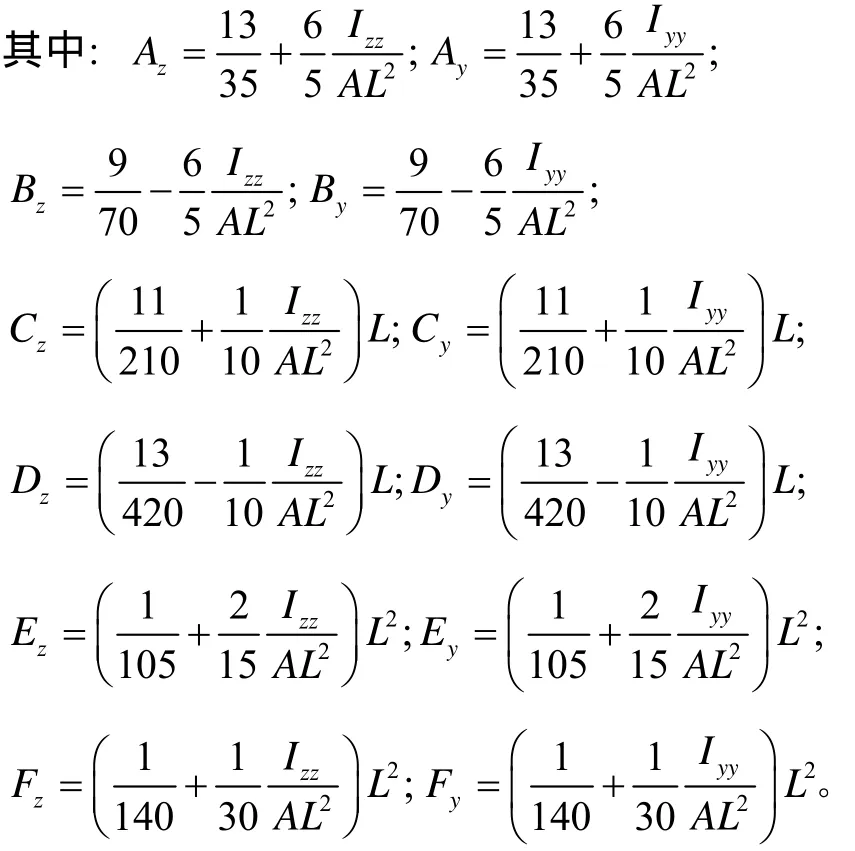
回轉矩陣為

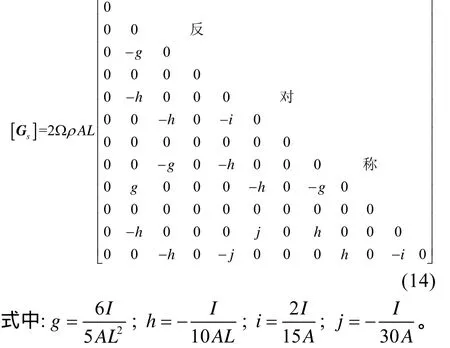
將上述單元矩陣疊加，即可得到系統矩陣。

2　運動微分方程的求解

系統運動微分方程的齊次式為

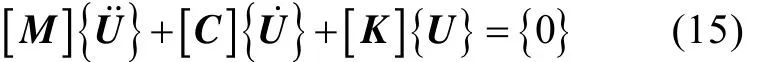
在結構動力學中，求解這種大型稀疏帶狀矩陣特征值問題的程序，通常要求在對稱矩陣情況下使用。而在轉子動力學中，由于軸承動力特性參數中包括交叉剛度和交叉阻尼，且二者往往并不相等，使得剛度矩陣［K］失去了對稱性，因此一般采用復模態理論求解轉子動力學方程。

復模態理論是將運動方程的齊次式化為1階微分方程組來求解，即令

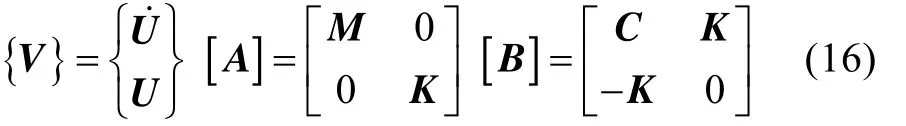
則運動方程的齊次式可改寫為

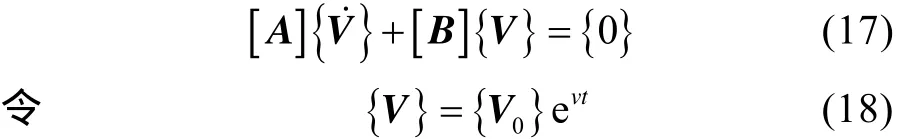
帶入式（17）可得

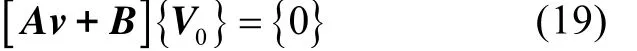
由此可求解特征值v及特征向量｛V0｝。特征值v即為系統在給定自轉角速度下的渦動頻率，且根據特征向量｛V0｝可得相應的模態振型。

3　MATLAB編程

3.1編程流程

根據上述對系統運動微分方程及其求解過程的分析，編寫MATLAB程序。

首先對轉子系統進行結點單元的劃分，以建立有限元模型。其次計算結點處的單元矩陣，并將單元矩陣按照結點位置進行疊加，形成系統整體矩陣，得到微分方程中的矩陣參數。最后根據支承情況，對系統剛度矩陣進行修正處理。在求解過程中，根據復模態理論對系統矩陣進行擴充，將運動方程轉化成1階微分方程組，然后可直接利用MATLAB中eig程序（求特征值和特征向量）進行求解。

程序具體流程如圖3所示。

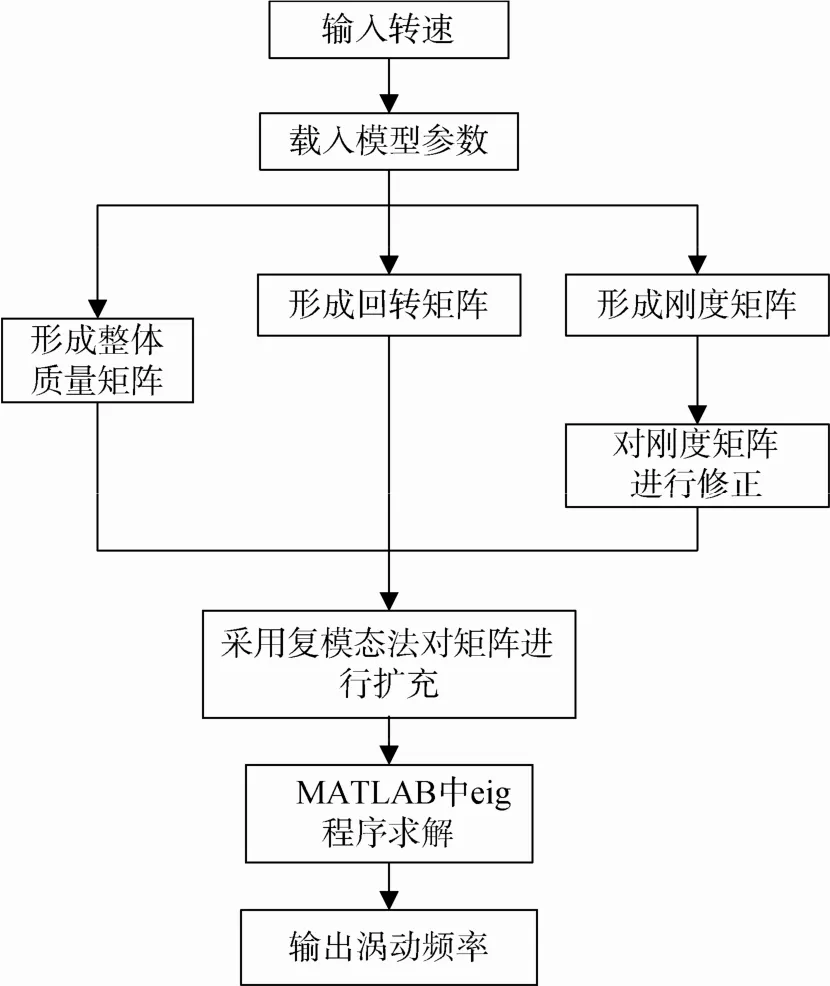
圖3　編程流程圖Fig. 3　Flowchart of programming

按照結點處為4自由度和6自由度狀態分別編程。4自由度和6自由度程序的單元疊加方式一致，但在對剛度矩陣進行修正時會有所差異。

3.24自由度剛度矩陣修正

對于一般的軸承單元，其剛度、阻尼系數矩陣分別為

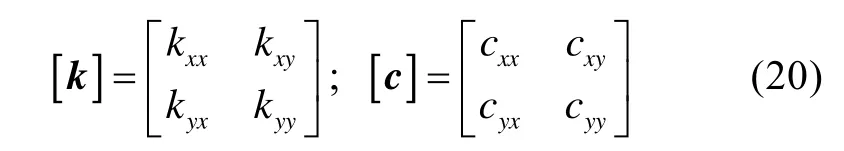
若假設系統具有N個結點，其間用N-1個軸段連接而成，則系統的位移向量由式（2）改寫為

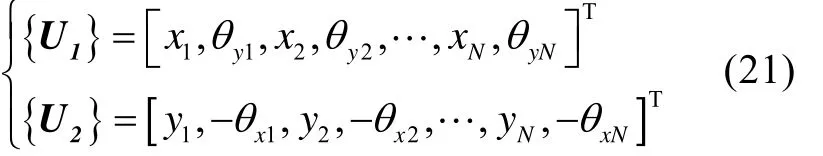
考慮支承處的軸承作用，則此時系統運動方程為

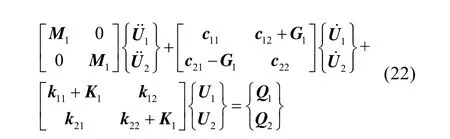
假設第j個結點為軸承單元，則在2N×2N階的矩陣［c11］，［c21］，［c12］，［c22］和［k11］，［k12］，［k21］，［k22］中，除了第2s（j）-1行和2s（j）-1列中有元素cxx，cxy，cyx，cyy，kxx，kxy，kyx，kyy外，其余元素都為零。

則運動微分方程的各個參數為如下形式

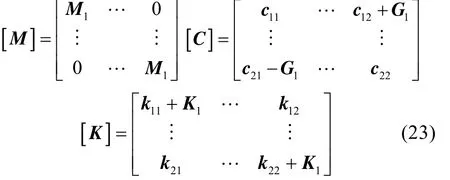
3.36自由度剛度矩陣修正

考慮軸承單元6個方向的連接剛度，則其剛度系數矩陣形式為

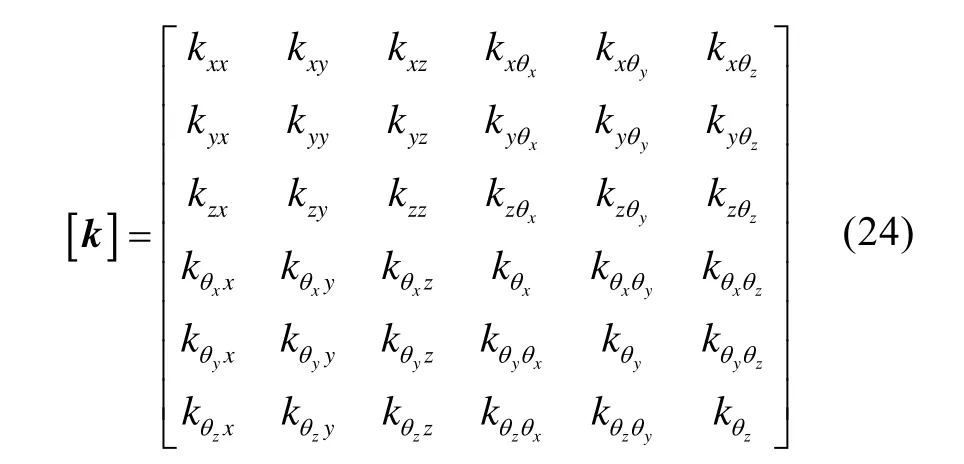
在對系統剛度矩陣進行修正時，可將軸承的剛度系數矩陣按照其結點位置直接疊加到系統矩陣中進行計算。

4　算例分析

ANSYS幫助文檔中VM254算例［9］的模型為典型的轉子動力學模型。它由剛性圓盤、變截面的彈性軸段及滑動軸承組成，具體結構見圖4。在變截面處、支承位置和圓盤位置設置結點，則可沿軸線自左至右將軸段劃分為18段，總計19個結點。模型具體參數可參考ANSYS幫助文檔。

ANSYS運行結果的坎貝爾圖如圖5所示。圖中交點的橫坐標即為臨界轉速值。應用所編寫的MATLAB程序對上述模型進行計算。按4自由度狀態得出的坎貝爾圖見圖6。

按6自由度狀態得出的坎貝爾圖見圖7。

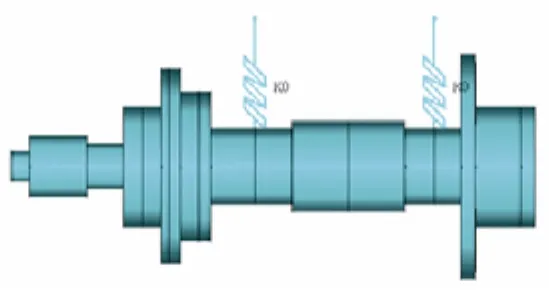
圖4　轉子模型Fig. 4　Rotor model

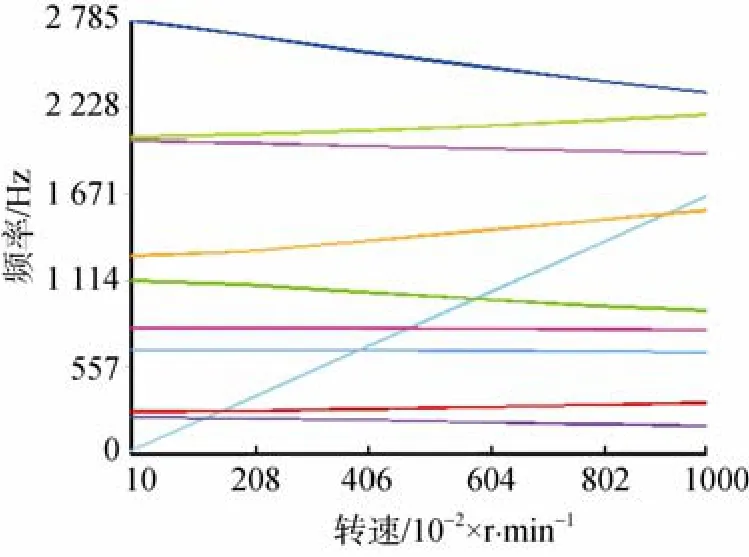
圖5　ANSYS得出的坎貝爾圖Fig. 5　Campbell diagram from ANSYS

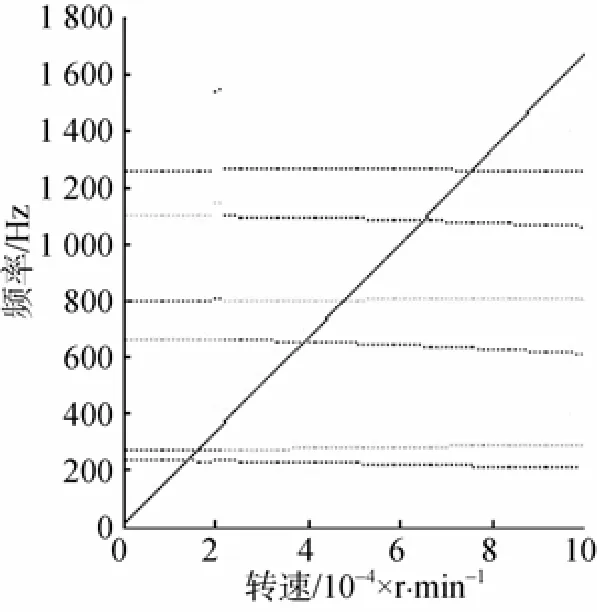
圖7　6自由度狀態的坎貝爾圖Fig. 7　Campbell diagram of six-degree-of-freedom state

在輸入轉速為105r/min時的渦動頻率計算結果如表1所示。

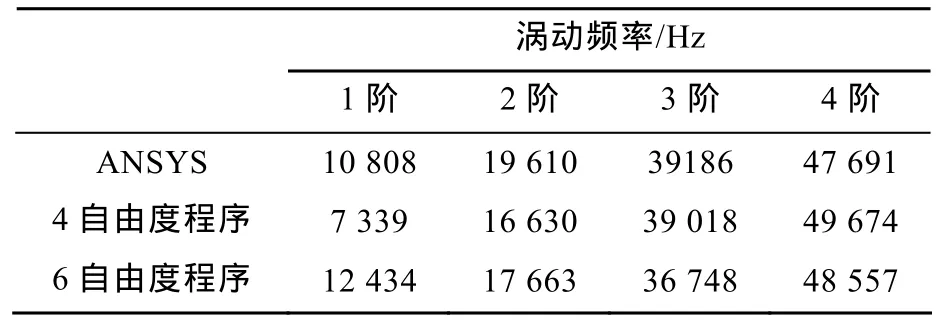
表1　渦動頻率計算結果Table 1　Calculation results of whirling frequency

對比三者間的坎貝爾圖可以看出，6自由度程序得出的結果與ANSYS比較吻合。通過分析在轉速為105r/min時的計算結果可以看出，6自由度程序所得結果較4自由度程序更接近ANSYS的計算結果。所以，可以認為6自由度程序是合理的，可以用來計算魚雷推進軸系的渦動頻率。

5　6自由度程序在魚雷推進軸系的應用

5.1魚雷推進軸系結構及其有限元模型

魚雷推進軸系結構如圖8所示。動力裝置與花鍵軸之間、花鍵軸與尾軸之間通過花鍵相連，推進器轉子安裝在尾軸上。花鍵軸及尾軸主要用于將動力裝置的輸出功率傳遞給推進器，而推進器工作時產生的推力通過推力軸承傳遞至雷尾殼體，推動魚雷航行。在花鍵軸與尾軸相連的一端裝有彈性花鍵套（圖中標記2）。尾軸的支撐是靠隔板的滾珠軸承和尾蓋處的滑動軸承，在滾珠軸承及滑動軸承外側都安裝了金屬橡膠隔振器（圖中標記5和9）。

魚雷推進軸系簡化模型（將推進器作為質量單元處理）如圖9所示。

建立魚雷推進軸系的有限元模型，可以沿軸線將花鍵軸和尾軸劃分為若干個結點，如圖10所示。對于彈性花鍵套，可以采用等效軸段法模擬其橫向剛度和轉角剛度。圖中，結點1為花鍵軸前端，與動力裝置相連； 結點2為花鍵套簡化位置； 結點8，9和10為彈性花鍵套簡化位置； 結點11和19為軸承支撐位置； 結點21為推進器安裝位置。

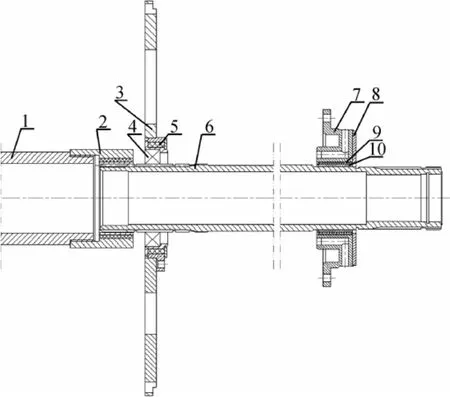
圖8　魚雷推進軸系結構Fig. 8　Structure of torpedo propulsion shafting

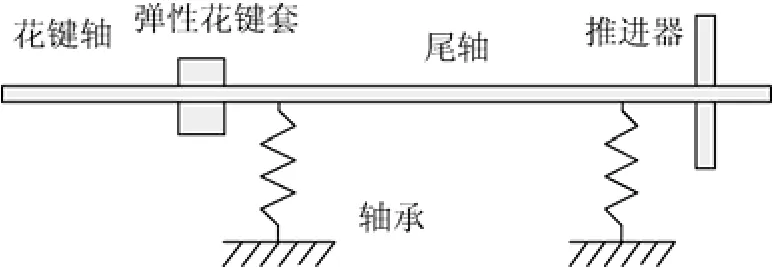
圖9　推進軸系簡化模型Fig. 9　Simplified model of torpedo propulsion shafting

圖10　花鍵軸和尾軸的結點劃分Fig. 10　Elements dividing of spline-shaft and tail-shaft

5.2計算結果與分析

應用6自由度MATLAB程序對魚雷推進軸系進行渦動頻率計算，得出的坎貝爾圖見圖11。

選取轉速1150 r/min，1500 r/min和2050 r/min時的前4階渦動頻率如表2所示。利用ANSYS軟件進行計算的結果見表3。對比推進軸系不同轉速下的前4階渦動頻率可得，MATLAB程序計算結果與ANSYS計算結果基本一致，證明該文所編程序是合理的。

6　結束語

根據轉子系統的運動微分方程，從2個方面進行編程，分別計算了結點為4自由度狀態和6自由度狀態時的結果。6自由度狀態考慮了結點在3個方向的位移和轉角，并在進行系統剛度矩陣修正時，對軸承剛度和阻尼系數的處理方式也比較完整，更接近于實際情況。

基于此程序，可以對轉子系統在其他實際狀態下進行渦動頻率及臨界轉速等因素的分析，也可進行后續的開發。

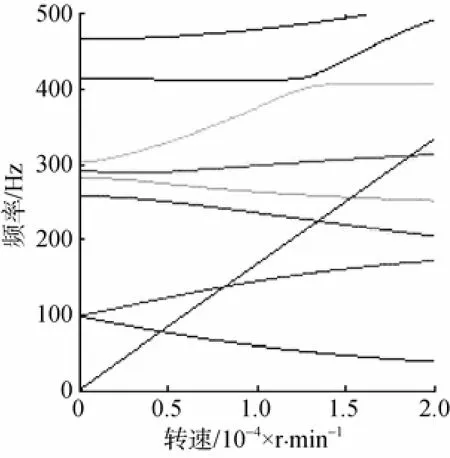
圖11　推進軸系坎貝爾圖Fig. 11　Campbell diagram of propulsion shafting

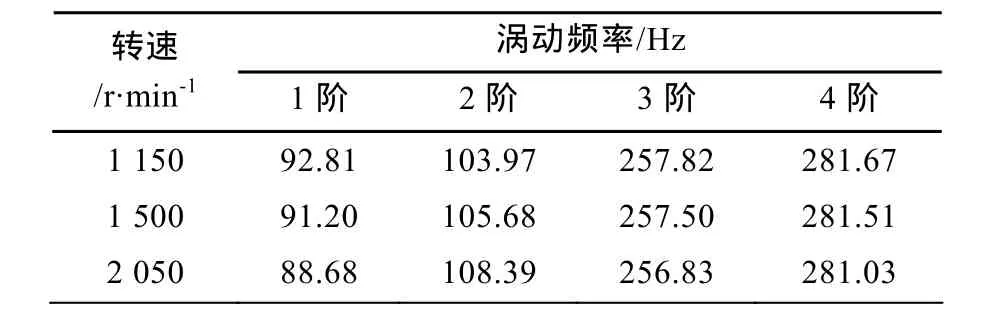
表2　MATLAB計算結果Table 2　Calculation results of MATLAB

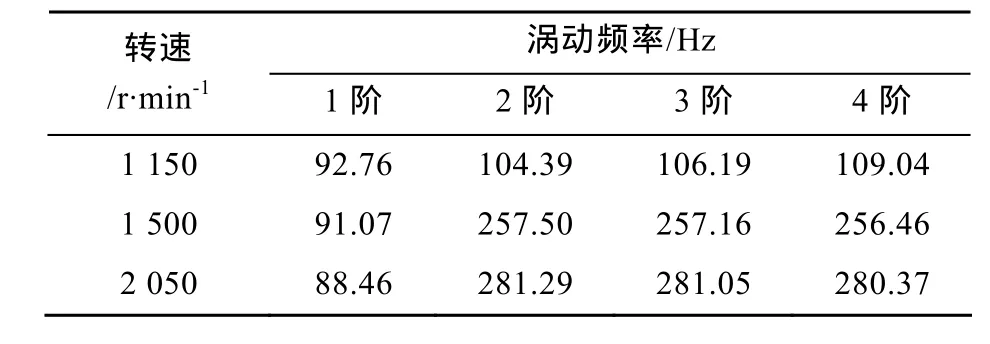
表3　ANSYS計算結果Table 3　Calculation results of ANSYS

［1］阮小麗. 基于傳遞矩陣法和有限元法的轉子動力學分析［J］. 機電工程技術，2011，40（3）： 71-73.

Ruan Xiao-li. Based on Transfer Matrix Method and the Finite Element Method Analysis of Rotor Dynamics［J］. Mechanical & Electrical Engineering Technology. 2011，40（3）： 71-73.

［2］鐘一諤. 轉子動力學［M］. 北京： 清華大學出版社，1984.

［3］王軍峰，孫康. 基于有限元法的轉子臨界轉速計算［J］.機械設計. 2012，29（12）： 10-13.

Wang Jun-feng，Sun Kang. Rotor Critical Speed Calculation Based on Finite Element Method［J］. Journal of Machine Design.2012，29（12）： 10-13.

［4］汪夢甫，王朝暉. 兩種質量矩陣在梁模態分析中差異的比較［J］. 地震工程與工程振動. 2006，26（6）： 84-86.

Wang Meng-fu，Wang Zhao-hui. Analysis of Differences Between Two Types of Mass Matrixes in Beam Modal Analysis［J］. Earthquake Engineering and Engineering Vibration. 2006，26（6）： 84-86.

［5］徐榮橋. 結構分析的有限元法與MATLAB程序設計［M］. 北京： 人民交通出版社，2005.

［6］車樹汶，陳權，樓松慶. 質量矩陣模式對橋梁自振頻率的影響［J］. 蘭州交通大學學報，2003，22（6）： 80-83.

Che Shu-wen，Chen Quan，Lou Song-qing. Influence of Mass Matrix Model on Natural Vibration Frequency of Bridges［J］. Journal of Lanzhou Jiaotong University，2003，22（6）： 80-83.

［7］董軍，劉旭紅，姚順忠，等. 基于虛功原理表達的空間梁單元剛度矩陣分析［J］. 西南林學院學報，2002，22（4）：59-62.

Dong Jun，Liu Xu-hong，Yao Shun-zhong，et al. Analysis of Element Stiffness Matrix About Space Beam-Element Based on Principle of Virtual Work［J］. Journal of Southwest Forestry College，2002，22（4）： 59-62.

［8］王勖成. 有限單元法［M］. 北京： 清華大學出版社，2003.

［9］Vaugh N M. The Dynamics of Rotor-Bearing Systems Using Finite Element［J］. Journal of Engineering for Industry，1976，98（2）：593-600.

（責任編輯： 陳曦）

Calculation of Whirling Frequency in Flexural Vibration of Torpedo Propulsion Shafting Based on MATLAB

ZHAO Qi1，2，YIN Shao-ping1，2，WANG Zhong1，2，GUO Jun1
（1. The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710075，China； 2. Science and Technology on Underwater Information and Control Laboratory，Xi′an 710075，China）

To avoid resonance，it is necessary to calculate whirling frequency of a rotor system. The input parameters of commercial finite element analysis（FEA）softwares are limited，and these softwares can not complete the analysis of special cases. In this paper，according to the differential equation of motion for a rotor system and its solution process，a program is coded to calculate the whirling frequency by the software MATLAB. Comparison between the results of MATLAB and ANSYS shows that this MATLAB program is reasonable，and it can be used to calculate whirling frequency in flexural vibration of torpedo propulsion shafting or to perform subsequent development.

torpedo propulsion shafting； flexural vibration； whirling frequency

TJ630.1

A

1673-1948（2015）01-0007-07

2014-05-14；

2014-07-10.

趙琪（1989-），男，在讀碩士，研究方向為魚雷總體技術.