水下航行器釋放機構動作可靠性分析

周　煒，　薛　來，　趙　敏

（1. 海軍駐昆明七五〇試驗場軍事代表室， 云南 昆明， 650051； 2. 昆明船舶設備研究試驗中心， 云南， 昆明，650051）

水下航行器釋放機構動作可靠性分析

周煒1，薛來2，趙敏2

（1. 海軍駐昆明七五〇試驗場軍事代表室， 云南 昆明， 650051； 2. 昆明船舶設備研究試驗中心， 云南， 昆明，650051）

水下航行器的釋放機構是該裝備的重要組成部分， 釋放機構能否正常動作， 是該裝備完成作戰任務的關鍵。該文以驗算點法為依據， 利用FREET機械可靠性分析軟件分析了釋放機構關鍵組成部件的可靠性， 所得結論為水下航行器釋放機構的設計提供參考。

水下航行器； 機械可靠性； 釋放機構； 驗算點法

0　引言

水下航行器的艙體設計有一個釋放機構， 其功能是在航行器發射一定時間后在水中打開艙體艙蓋， 艙體內的組件在負浮力作用下脫離艙體完成作戰任務。該機構主要組成零件包括鎖定機構、動力產生裝置、連桿、轉軸及曲柄， 當釋放機構啟動時，首先是鎖定機構解鎖， 然后動力裝置產生驅動力使連桿運動， 連桿固定在轉軸一端帶動轉軸轉動， 固定在另一端的曲柄在轉軸轉動下運動， 從而將艙蓋打開， 完成釋放動作。釋放機構是水下航行器的重要組成部分， 其能否正常動作是水下航行器完成作戰任務的關鍵。釋放機構的可靠性設計通常采用安全系數法， 由于該方法有很大的盲目性和保守性［1］，導致設計結果存在不合理之處。文章基于驗算點法建立了釋放機構可靠性計算模型， 利用FREET軟件對現有釋放機構的可靠性進行計算分析， 得出其可靠度， 通過分析結果可有效指導設計。

1　理論依據

1.1機械可靠性計算模型

機械產品進行可靠性設計分析時， 根據其設計功能建立相對應的狀態函數g（X）， 當g（X）可看作只有廣義應力r和廣義強度l兩個隨機變量時

機械產品在任意時刻是否能夠保持其規定功能， 在數學上可用狀態函數的取值是否大于0來決定， 把產品狀態分為可靠狀態（用g（X）＞0表示）和失效狀態（用g（X）＜0表示）， 而產品可靠狀態向失效狀態轉換的臨界狀態（用g（X）=0表示）稱為極限狀態， g（X）=0稱為極限狀態方程。在解析幾何中， 極限狀態方程是坐標系中的一個多維曲面，稱為極限狀態曲面［2］。

在機械可靠性中， 常用可靠度指標β代替可靠度， 它被定義為狀態函數的均值與標準差之比， 即

當基本隨機變量均服從正態分布， 且狀態方程為基本變量的線性函數時， 可靠度為

其中， Φ（·）為標準正態分布函數。

1.2一次二階矩法

一次二階矩（first order second moment， FOSM）法在機械結構可靠性領域得到了廣泛應用， 經過幾十年的研究發展已成為世界各國結構安全標準、規范的基礎。驗算點法是FOSM法的一種， 在1974年由Hasofer和Lind提出［3］， 他們將可靠性指標β定義為標準正態空間內坐標原點到極限狀態曲面的最短距離， 并將最短距離在極限狀態面對應當點定義為設計驗算點（most probabile point， MPP）使得對應于同一失效面建立失效方程的不同表達式可得唯一可靠性指標。驗算點法能夠考慮非正態隨機變量， 在計算工作量差不多的條件下， 可對可靠度指標進行精度較高的近似計算。具體算法如下。

1） 假定初始驗算點

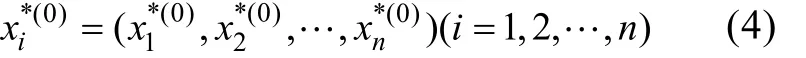
2） 根據設計驗算點， 計算非正態隨機變量的等效正態分布參數；

3） 計算可靠度指標

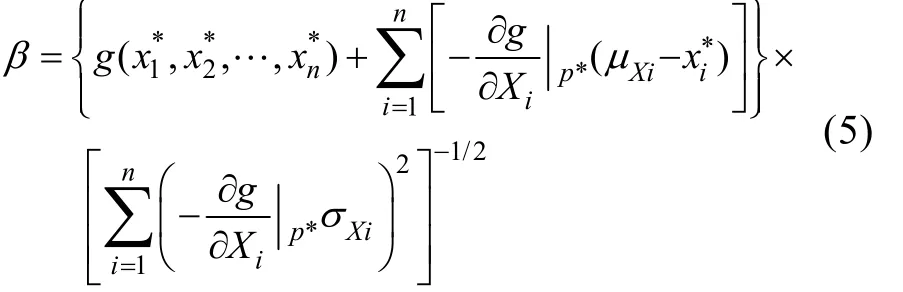
4） 計算重要度系數

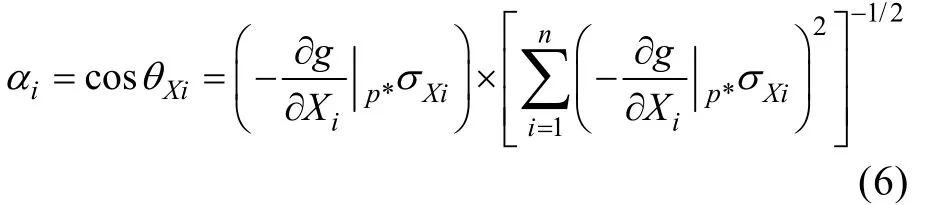
5） 計算新的驗算點

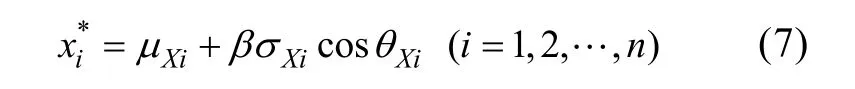
1.3FREET機械可靠性軟件

FREET（feasible reliability engineering tool）軟件用于對簡單與復雜機械結構產品進行統計分析及可靠性和敏感性分析。該軟件的特點是在精度要求約束下有效減少仿真樣本量， 使設計人員定義的工程問題能以相對簡單快速的方法進行評估，可極大減少設計人員的計算時間。FREET可自定義狀態方程， 計算可靠度所用方法為驗算點法。

2　釋放機構可靠性計算模型

2.1釋放機構組成

釋放機構主要由曲柄、轉軸、連桿及鎖定機構構成， 如圖1所示。

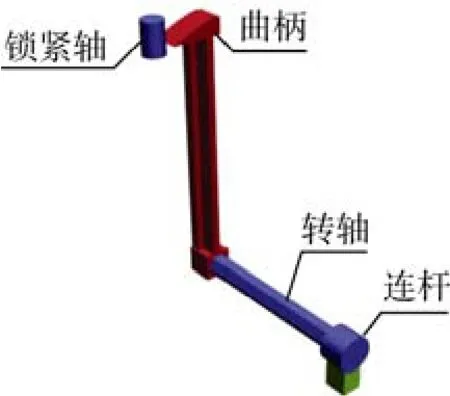
圖1　釋放機構示意圖Fig. 1　Schematic of releasing device

曲柄負責將氣源驅動下轉軸的旋轉動作傳遞給艙蓋， 實現釋放機構艙蓋的打開與關閉。轉軸負責在連桿驅動下旋轉， 帶動艙蓋運動， 實現釋放機構艙蓋的打開與關閉。連桿負責將氣源產生裝置產生的動力傳遞給轉軸， 將直線運動轉變為轉軸的旋轉運動。釋放機構設計有鎖定機構， 安裝好機構內待釋放組件并關閉艙蓋后， 對釋放機構進行鎖定， 開艙前要先解鎖， 才能打開艙蓋，避免艙蓋在發射氣流（或水流）沖擊下產生誤動作。艙蓋關閉后， 其外形與航行器殼體外表面共形， 可減小航行阻力。

2.2狀態方程

2.2.1曲柄

對曲柄進行受力分析后， 確定曲柄的主要受力為拉伸應力。曲柄材料采用06Cr19Ni10， 其截面如圖2所示。則曲柄的拉伸應力為

式中： ε為拉伸應力； F為拉力最大值； a1， b1， c， h為曲柄截面尺寸。

根據應力-強度干涉理論， 以應力極限狀態表示的狀態方程為

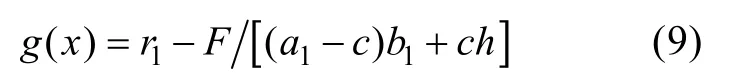
其中， r1為曲柄材料強度。

2.2.2轉軸

對轉軸進行受力分析后， 確定轉軸的主要受力為扭轉應力。轉軸材料采用06Cr19Ni10， 其截面可近似正八角形（見圖3）。則轉軸所受的扭轉應力

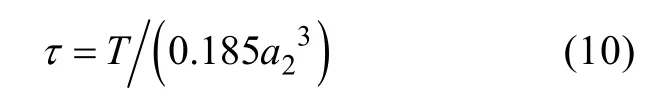
式中： τ為轉軸承受的扭轉應力； T為扭矩； a2為八角形厚度。

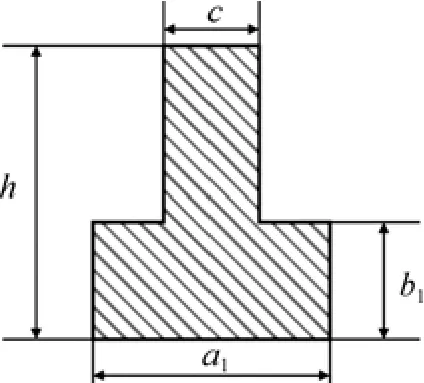
圖2　曲柄截面圖Fig. 2　Section of crank

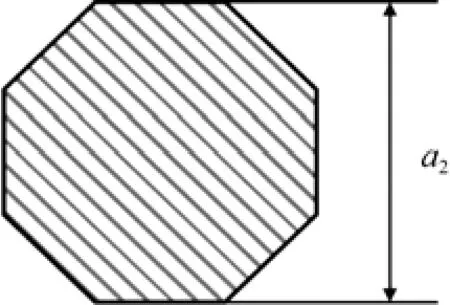
　圖3　轉軸截面圖Fig. 3　Section of shaft

根據應力-強度干涉理論， 以應力極限狀態表示的狀態方程為

其中， r2為轉軸材料強度。

2.2.3連桿

對連桿進行受力分析后， 確定轉軸的主要受力為剪切應力。連桿材料采用45號碳素鋼， 其截面為矩形， 見圖4。則連桿所受的剪切應力為

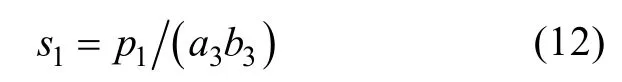
式中： s1為連桿剪切應力； p1為連桿承受的剪切載荷； a3為連桿截面寬度； b3為連桿的截面厚度。

根據應力-強度干涉理論， 以應力極限狀態表示的狀態方程為

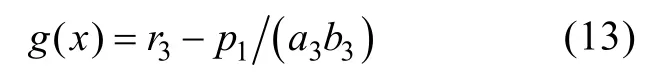
式中： r3為轉軸材料剪切強度。

2.2.4鎖定機構

對鎖緊裝置進行受力分析后， 確定裝置的主要受力零件鎖緊軸的受力為剪切應力。鎖緊軸材料采用06Cr19Ni10， 其截面為圓形， 如圖5所示。則鎖緊軸的剪切應力為

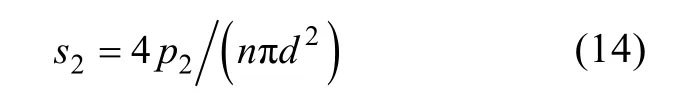
式中： s2為鎖緊軸剪切應力； p2為鎖緊軸承受的剪切載荷； d為鎖緊軸截面直徑； n為剪切面數。

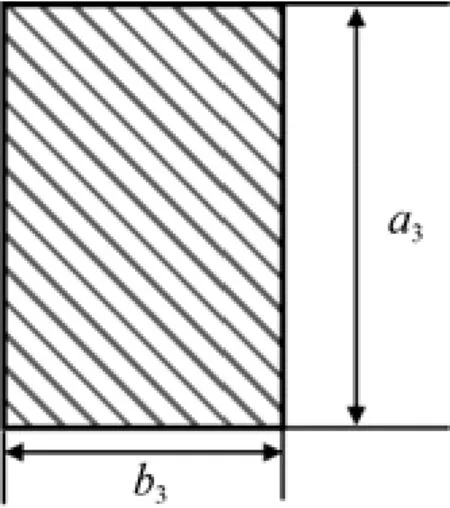
圖4　連桿截面圖Fig. 4　Section of connecting rod

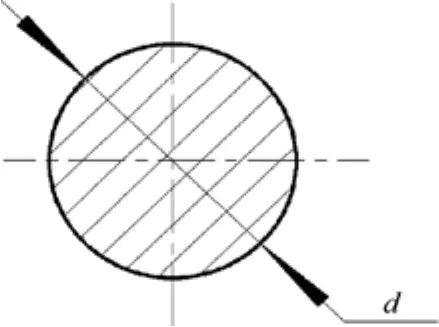
圖5　鎖緊軸截面圖Fig. 5　Section of clamp　axis

根據應力-強度干涉理論， 以應力極限狀態表示的狀態方程為

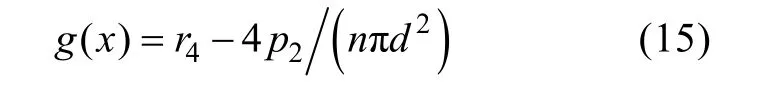
式中： r4為鎖緊軸材料剪切強度。

3　釋放機構可靠度計算

3.1設計參數數據的統計處理

為簡化計算， 假設基本隨機變量相互獨立且服從正態分布， 這是因為正態分布能反映多數零部件的實際情況， 并且即使當強度與應力均為非正態分布時， 若采用正態分布假設， 一般將得到偏于保守的結果［1］。

3.2各部分可靠度計算

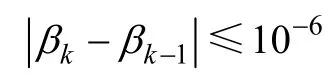
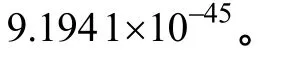
釋放機構中任一部分發生失效， 整個機構均不能正常工作， 因此認為釋放機構的可靠性模型為串聯模型， 則釋放機構的可靠度為

計算得釋放機構可靠度約為1.000。

表1　釋放機構各部件的參數及可靠度計算結果Table 1　Parameters and calculated reliabilities of releasing device′s components

4　計算結果分析

經計算釋放機構可靠度約為1.000， 而實際上該機構的可靠度規定值為0.99， 可以看出其設計較為保守。對釋放機構的各組件重新進行可靠性設計， 得出了當釋放機構各組件可靠度達到0.999 9時的設計參數， 并計算出按新的設計參數計算出的機構減少的質量， 如表2所示。從表2可以看出， 原本各組件尺寸設計過大， 導致質量的增加以及不必要的材料浪費。

表2　釋放機構各部件的可靠性設計結果Table 2　Designed reliabilities of releasing device′s components

5　結束語

文章在基本隨機參數的概率特性已知情況下，應用驗算點法對現有釋放機構可靠度進行計算，找出釋放機構可靠性設計的不足， 通過上述各零件可靠度分析可知， 采用可靠性設計結果與常規設計相比， 能極大的節省材料， 降低產品質量，但從計算過程可知， 要保證這一高可靠度必須使材料的強度和應力的均值、標準差保持穩定不變，即可靠性設計的先進性是要以材料制造工藝的穩定性及對載荷測定的準確性為前提條件。各零件的可靠性設計中還進行了敏感分析， 以便在今后的設計中注意控制那些影響顯著的參數。文中提供的可靠性分析方法對水下航行器機械零件設計的指導具有通用性， 可以在未來水下航行器的可靠性設計中加以應用。

［1］ 劉惟信. 機械可靠性設計［M］. 北京： 清華大學出版社，1996.

［2］ 張建國， 蘇多， 劉英衛. 機械產品可靠性分析與優化［M］. 北京： 電子工業出版社， 2008.

［3］ Hasofer A M， Lind N C. An Exact and Invariant First Order Reliability Format［J］. Journal of Engineering Mechanics， 1974， 100（EMI）： 111-121.

［4］ Zotos J. Mathematical Modeling of the Chemical， Mechanical and Physical Properties of Engineering Alloys［M］. Massachusetts Toronto： D.C. Health and Company Lexington， 1977.

（責任編輯： 陳曦）

Mechanical Reliability Analysis of Releasing Device for Underwater Vehicle

ZHOU Wei1，XUE Lai2，ZHAO Min2
（1. Navy Representative Office Stationed in Kunming 750 Test Range， Kunming 650051， China； 2. Kunming Shipborne Equipment Research & Test Center， Kunming 650051， China）

Whether an underwater vehicle can complete its mission depends on the normal operation of its releasing device. In this paper， the mechanical reliability analysis software FREET is employed to analyze the reliability of the key components of the releasing device with the JC method. The results obtained may be a reference for further design of an underwater vehicle.

underwater vehicle； mechanical reliability； releasing device； JC method

TJ630

A

1673-1948（2015）06-0410-04

10.11993/j.issn.1673-1948.2015.06.003

2015-07-26；

2015-09-13.

周煒（1979-）， 男， 工程師， 研究方向為水中兵器研制過程管理方法.