反魚雷魚雷末制導捕獲概率建模與仿真

蕭叢杉，　楊惠珍

（1. 西北工業(yè)大學 航海學院， 陜西 西安， 710072； 2. 水下信息與控制重點實驗室， 陜西 西安， 710075）

反魚雷魚雷末制導捕獲概率建模與仿真

蕭叢杉1，2，楊惠珍1，2

（1. 西北工業(yè)大學 航海學院， 陜西 西安， 710072； 2. 水下信息與控制重點實驗室， 陜西 西安， 710075）

建立了一種反魚雷魚雷（ATT）末制導捕獲概率數(shù)學模型。通過分析末制導交班時刻ATT和來襲魚雷的位置誤差，將捕獲概率問題描述成一個二重概率密度函數(shù)在導引頭自導扇面內(nèi)的積分問題，對積分區(qū)域進行近似化簡，得到了一個與位置誤差、自導作用距離、雷目距離和自導扇面角4個變量有關(guān)的ATT捕獲概率解析表達式。最后通過仿真定量分析了上述4個變量對ATT捕獲概率的影響。

反魚雷魚雷； 末制導； 捕獲概率； 概率積分

0　引言

反魚雷魚雷（anti-torpedo torpedo， ATT）作為主動防御型硬殺傷武器， 已成為當前各國海軍研究和發(fā)展的重點武器之一。由于目標來襲魚雷具有速度快、體積小、機動性強等特點， ATT與來襲魚雷對抗時間短， 從而要求ATT全彈道精確導引和一次性攻擊成功， 沒有機會進行再搜索［1］。因此， ATT的末制導捕獲概率分析是ATT彈道設(shè)計和作戰(zhàn)效能分析的一個重要課題。

ATT的捕獲概率是指ATT攔截目標過程中，來襲目標落在導引頭最大導引距離和自導扇面范圍內(nèi)的概率［2］。ATT對目標的捕獲概率和發(fā)射艇的目標探測精度、ATT導引頭探測精度以及目標特性等密切相關(guān)。

目前， 關(guān)于捕獲概率問題的研究大多集中在導彈及反導系統(tǒng)領(lǐng)域， 主要的研究方法大多是將末制導雷達覆蓋目標的概率近似為導彈對目標的捕獲概率， 通過分析雷達搜索區(qū)和導彈能捕獲目標的自控終點散布區(qū)域來建立捕獲概率的計算模型。文獻［3］給出了目標散布區(qū)域的數(shù)學表達式，計算了單枚和多枚導彈的捕獲概率。文獻［4］對自控終點誤差、目標散布、現(xiàn)在點射擊方式進行了綜合討論。通過計算搜索扇面與目標散布區(qū)域的相交面積和整個目標散布區(qū)面積之比來計算捕獲概率， 文獻［5］將判斷目標被捕獲的問題轉(zhuǎn)換為判斷導彈自控終點分布問題， 建立了基于自控終點誤差模型的捕獲概率計算方法。文獻［6］利用蒙特卡洛法計算自控終點導彈的位置捕獲概率。文獻［7］將導彈扇面搜索區(qū)簡化為矩形區(qū)， 對純方位發(fā)射導彈的側(cè)向捕獲概率進行討論。文獻［8］在文獻［7］的基礎(chǔ)上， 采用解析幾何分析法， 綜合考慮目標方位誤差， 給出純方位發(fā)射導彈的捕獲概率的計算模型。文獻［9］分析了導彈系統(tǒng)的誤差源及特性和導引頭動態(tài)視場， 在此基礎(chǔ)進行捕獲概率的計算。文獻［10］綜合考慮攔截器和目標散布誤差， 建立捕獲概率的解析表達式， 并將捕獲概率問題轉(zhuǎn)化為求解三重概率積分的數(shù)學問題， 給出了明確的概率積分計算公式、積分區(qū)域表達式以及概率積分的具體解析過程。

關(guān)于魚雷和反魚雷魚雷的捕獲概率問題的相關(guān)研究還比較少， 多數(shù)文獻采用蒙特卡洛法來計算捕獲概率值， 這類方法雖然克服了武器系統(tǒng)復雜、涉及因素眾多等難題， 易于實現(xiàn)， 但同樣存在計算量大、不易掌握規(guī)律， 難以形成理論體系等缺點。文獻［11］建立了蛇形搜索下雙雷齊射攻擊與互導的數(shù)學模型， 利用蒙特卡洛法分別計算了不同主航向間距下的單雷攻擊和齊射攻擊的捕獲概率。文獻［12］對網(wǎng)絡(luò)魚雷和復合搜索面進行了研究， 設(shè)計了網(wǎng)絡(luò)系統(tǒng)的組成方案并對其進行效能分析， 分別給出了網(wǎng)絡(luò)魚雷和非網(wǎng)絡(luò)魚雷的捕獲概率公式并對其計算結(jié)果進行了對比。文獻［13］著重分析了火箭助飛魚雷的搜索域、魚雷落點散布和目標散布3個因素， 構(gòu)建了前置點射擊和現(xiàn)在點射擊2種方式下， 火箭助飛魚雷水平面捕獲概率的數(shù)學解析模型。但沒有考慮末制導時魚雷自導頭的有限捕獲范圍問題。文獻［14］利用蒙特卡洛法進行仿真， 討論了不同敵舷角范圍內(nèi)自導作用距離的不確定性對主動聲自導魚雷捕獲概率的影響。文獻［2］使用蒙特卡洛法對聲自導魚雷的捕獲概率進行了仿真分析。文獻［15］指出了傳統(tǒng)捕獲概率計算方法的局限性， 在分析目標和魚雷誤差散布的基礎(chǔ)上， 通過等概率分隔各參數(shù)誤差的方法計算主動自導魚雷多次連續(xù)捕獲概率，其計算精度受到誤差等概率分隔數(shù)影響較大。

文中結(jié)合反魚雷魚雷的實際情況， 研究ATT的末制導捕獲概率建模問題， 首先給出了ATT末制導捕獲概率的定義， 將捕獲概率問題描述成一個二重概率密度函數(shù)在導引扇面內(nèi)的積分問題，然后利用近似積分區(qū)域的方法建立了ATT捕獲概率的解析表達式， 基于該解析模型， 利用計算機仿真分析了ATT自導頭最大捕獲距離、自導扇面角、雷目位置誤差和雷目距離對ATT捕獲概率的影響。

1　捕獲概率的數(shù)學描述

如圖1所示， 考慮地面坐標系水平面O0x0z0內(nèi)的情況， ATT和來襲魚雷的位置散布均服從正態(tài)分布， 假設(shè)ATT分布中心的位置為（xT0，zT0），用矢量rT0表示， 位置誤差協(xié)方差矩陣為PT； 目標來襲魚雷分布中心的位置為rM0=（xM0，zM0），位置誤差協(xié)方差矩陣為PM。因此， ATT位置矢量rT和目標位置矢量rM的概率密度函數(shù)分別表示為

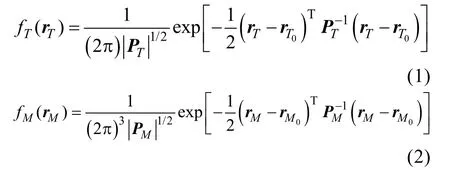
要使導引頭發(fā)現(xiàn)目標， 則目標需進入導引頭有效作用范圍內(nèi)， 即目標要落入自導扇面中。魚雷導引頭安裝在頭部， 聲軸方向與雷體縱軸重合，因此， 導引頭能否捕獲到目標取決于下面2個條件： 1） 雷目距離小于或等于自導頭最大作用距離；2） 自導頭聲軸與目標視線（light of sight， LOS）的夾角ε小于二分之一自導扇面角。因此， ATT的捕獲概率P可以表示為

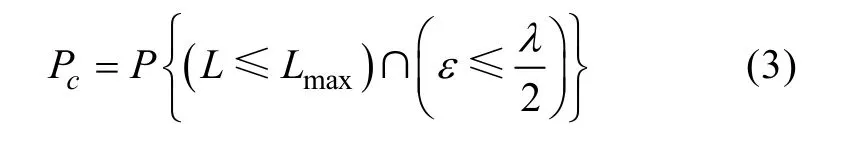
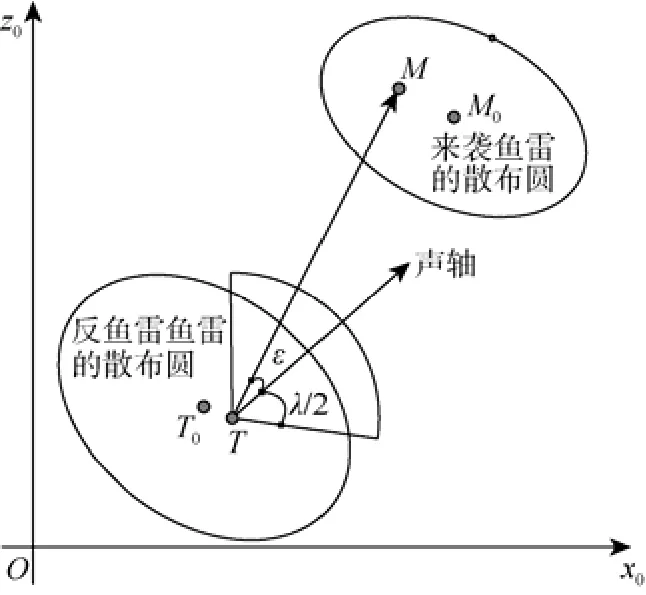
圖1　反魚雷魚雷（ATT)捕獲目標的條件Fig. 1　Conditions of target acquisition for an anti-torpedo torpedo(ATT)

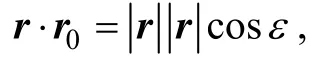
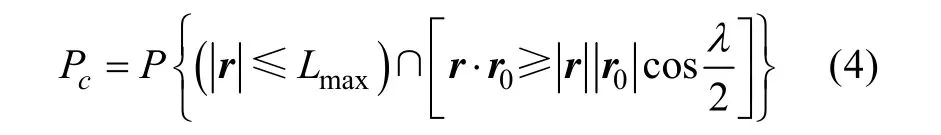
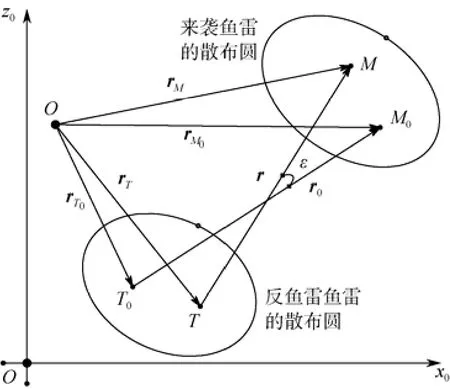
圖2　ATT和目標位置誤差分布Fig. 2　Position error distribution between ATT and target

由上式可知， ATT捕獲概率描述成ATT與目標的相對位置矢量滿足一定條件的概率， 通過在一定范圍內(nèi)對相對位置矢量的概率密度函數(shù)進行積分即可計算出此概率。

假設(shè)ATT的位置矢量和目標位置矢量相互獨立， 則相對位置矢量r的概率密度函數(shù)可以表示為

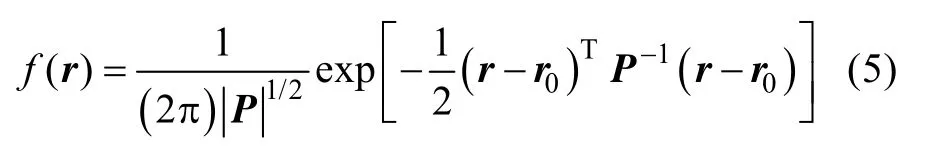
式中： r0為相對位置矢量的均值矢量； P為協(xié)方差矩陣， 有

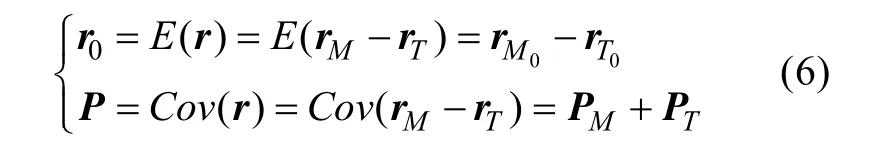
因此， 捕獲概率cP可以表示成相對位置矢量r的概率密度函數(shù)的二重積分

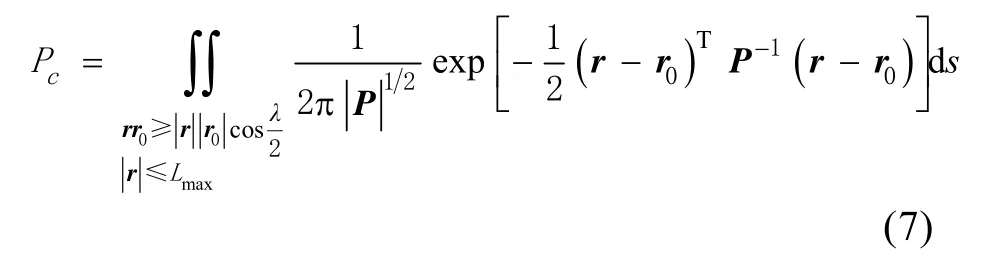
捕獲概率的計算問題就轉(zhuǎn)化為一個數(shù)學問題：求協(xié)方差矩陣為P、均值向量為r0的二維正態(tài)隨機向量r與常向量r0間夾角小于λ/2， 且r的長度小于Lmax的概率。如圖3所示， 滿足上面條件的矢量r的全體構(gòu)成一個以r0為中線， λ/2為半角， Lmax為半徑的扇面， 捕獲概率cP就是隨機矢量r落在該扇形內(nèi)的概率。

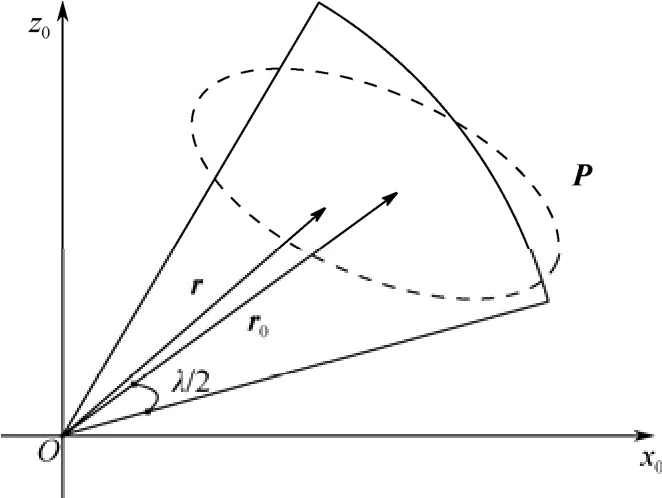
圖3　聯(lián)合誤差橢圓和扇面Fig. 3　Combined error ellipse and sector

2　捕獲概率計算

為了便于概率計算， 定義一種新的目標視線坐標系O-xszs， 原點O位于ATT分布中心， Oxs軸由ATT分布中心指向目標來襲魚雷分布中心， 即視線r0方向， Ozs軸在由地心、ATT分布中心和

2.1視線坐標系中的捕獲概率目標來襲魚雷分布中心構(gòu)成的平面內(nèi)垂直于Oxs軸， 指向左為正（從ATT尾部觀察）， 如圖4所示。

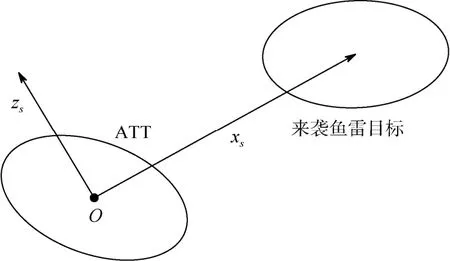
圖4　新定義的視線坐標系SFig. 4　A newly defined sight coordinates S

設(shè)視線坐標系S的兩坐標軸單位矢量分別為

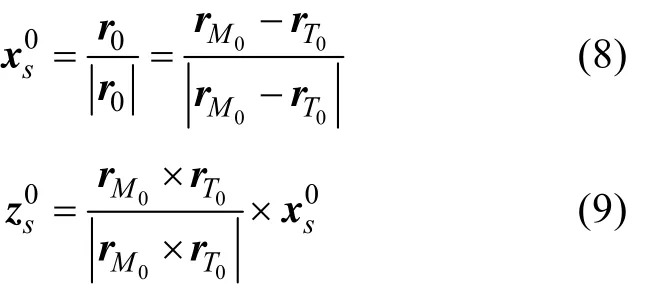
地面系到視線坐標系S的坐標轉(zhuǎn)移矩陣為

通過上面的坐標轉(zhuǎn)移矩陣， 可以將地面坐標系中的r0及P在S中表示為

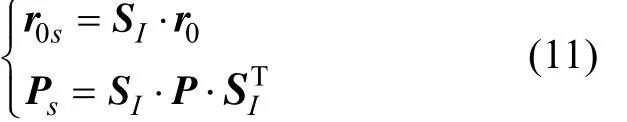
從視線坐標系定義可知， 矢量r0s的zs分量為零， 可以寫為

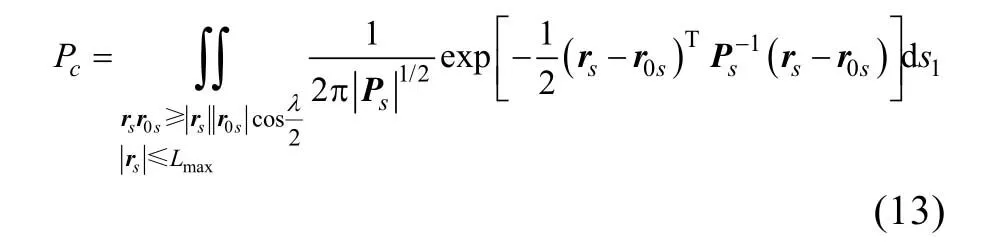
積分區(qū)域是以Lmax為半徑， λ/2為半扇面角，扇面角的角平分線落在Oxs軸上的 一個扇面， 如圖5所示。

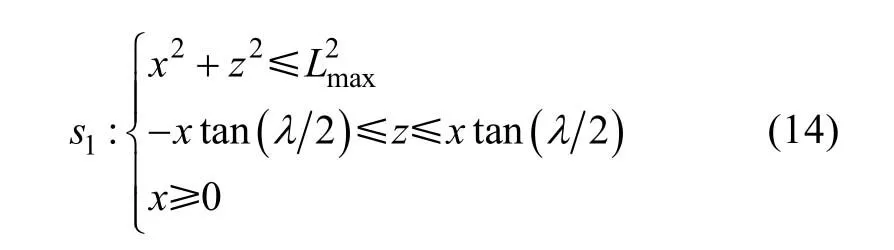
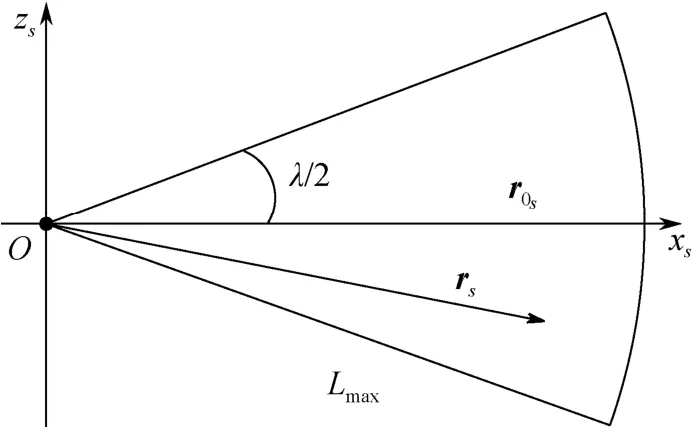
圖5　捕獲概率積分區(qū)域表示Fig. 5　Integration area of acquisition probability

為便于捕獲概率的計算， 有必要假設(shè)視線坐標系中xs視線方向的位置誤差與zs方向的位置誤差不相關(guān)， 即聯(lián)合誤差協(xié)方差矩陣Ps為對角矩陣

則捕獲概率可寫成下式

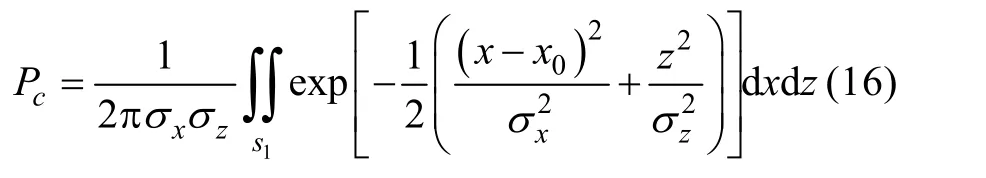
在實際情況中， 可以通過坐標旋轉(zhuǎn)將協(xié)方差矩陣轉(zhuǎn)換成對角陣［10］。

2.2積分區(qū)域近似

由圖6可見， 積分區(qū)域扇形的自導扇面角較小， 而最大捕獲距離較長， 因此， 在計算cP時，可以把積分區(qū)域近似為一矩形區(qū)域

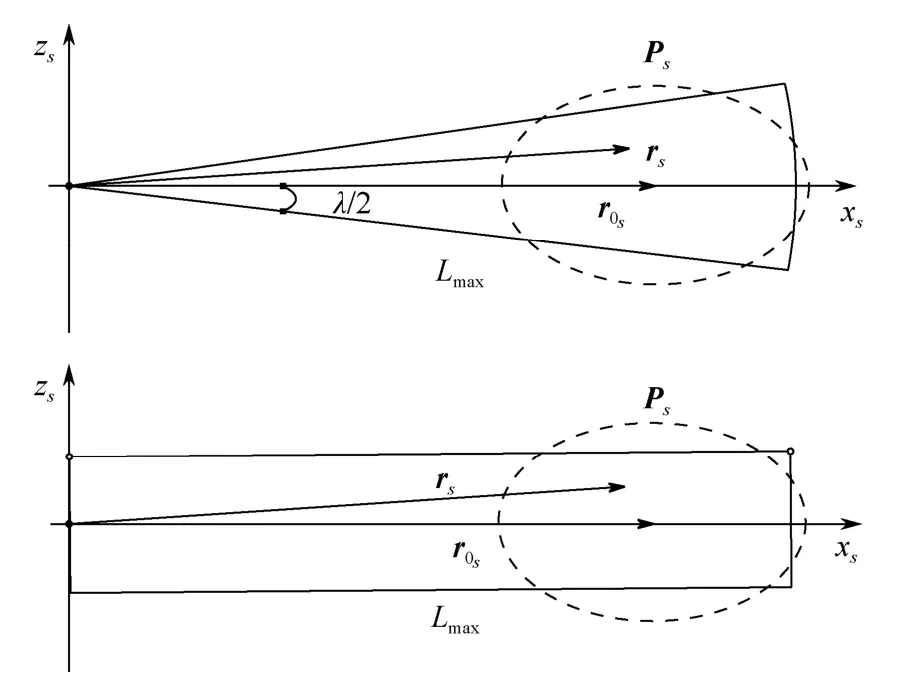
圖6　用矩形近似扇形積分區(qū)域示意圖Fig. 6　Schematic of approximating sectorial integration area to rectangular one

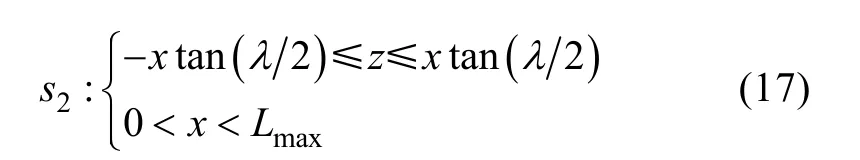
由于視線坐標系中xs方向的位置誤差與zs方向位置誤差不相關(guān)， 捕獲概率可以表示為

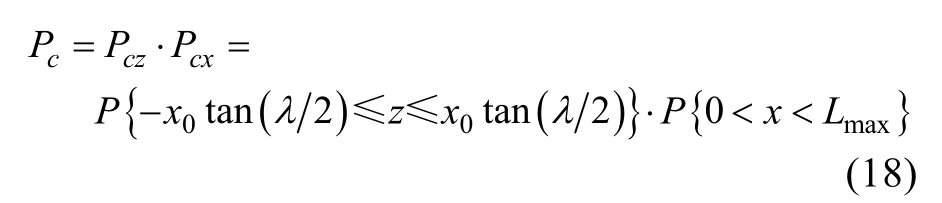
其中

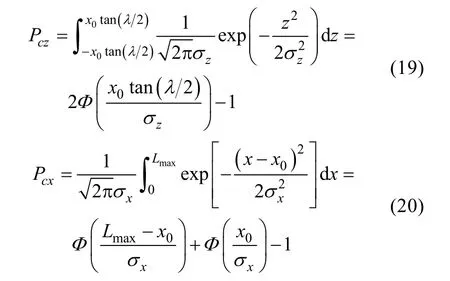
式中： Φ表示標準正態(tài)的分布函數(shù)。

將式（19）和式（20）代入式（18）， 可得捕獲概率

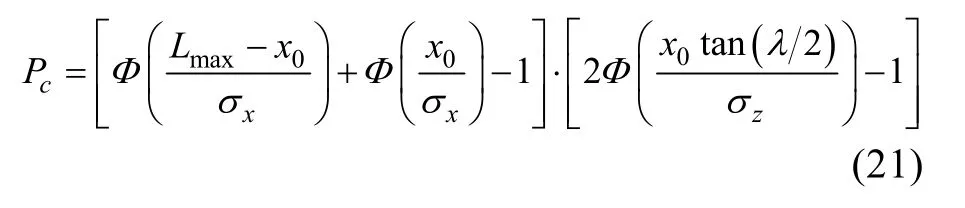
3　仿真結(jié)果與分析

式（16）是捕獲概率的積分表達式， 式（21）是捕獲概率的近似表達式。在仿真過程中， 對式（16）的求解需要采用數(shù)值積分的方法， 而式（21）只需將各參數(shù)代入公式中計算即可得到捕獲概率的近似解。

3.1積分區(qū)域近似算法精度

把利用數(shù)值積分計算的式（16）的值作為真實值， 與式（21）的計算結(jié)果進行對比可以分析積分區(qū)域近似算法的精度。

這說明將積分區(qū)域近似時， 引入的誤差不大，在工程實際中進行區(qū)域近似是可行的。

3.2捕獲概率的影響因素

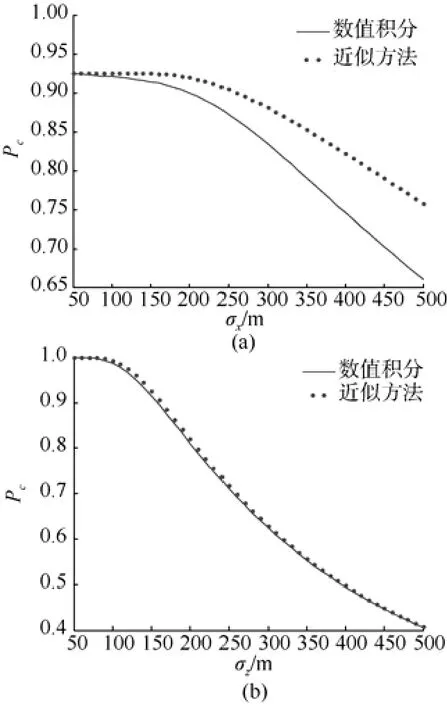
圖7　積分近似結(jié)果和精確計算結(jié)果對比Fig. 7　Comparison between approximate integration results and accurate ones

由捕獲概率的表達式（21）可以看出， 影響捕獲概率的因素主要有以下4個： 1） ATT與來襲魚雷分布中心間的距離x0； 2） ATT導引頭最大自導作用距離Lmax； 3） ATT導引頭自導扇面角λ； 4） ATT制導精度和目標探測精度。

下面分析上述四因素對捕獲概率的影響。仿真參數(shù)設(shè)為λ=30°，Lmax=1500 m ， σx=σz=150 m ，改變x0的取值， 分析彈目距離對捕獲概率的影響。

圖8為捕獲概率Pc隨彈目距離x0的變化曲線， 由圖可以看出， 捕獲概率Pc隨著彈目距離x0的增大， 先增大， 在達到極大值后開始急速下降至0。當距離x0從0增大到1 148 m時， Pc從0增大到最大值0.95， 當x0再增大時， Pc則迅速下降到0， 這是由于來襲目標魚雷超出了ATT的最大捕獲距離而無法捕獲造成的。

仿真參數(shù)設(shè)為λ=30°，x0=1000m， σx=σz=150 m。改變Lmax的取值， 分析最大自導作用距離對捕獲概率的影響。

圖9為捕獲概率Pc隨著Lmax的變化曲線。由圖可以看出， 當Lmax＜550 m時， 捕獲概率接近于0， 當Lmax＞1450 m 時， 最大自導作用距離對捕獲概率幾乎沒有影響， 這也符合誤差理論中的3σ法則， 即有效捕獲距離幾乎全部落在x0±3σx內(nèi)。仿真參數(shù)設(shè)為Lmax=1500 m ， x0=1000 m ，σx=σz=150 m 。改變λ的取值， 分析自導扇面角對捕獲概率的影響。

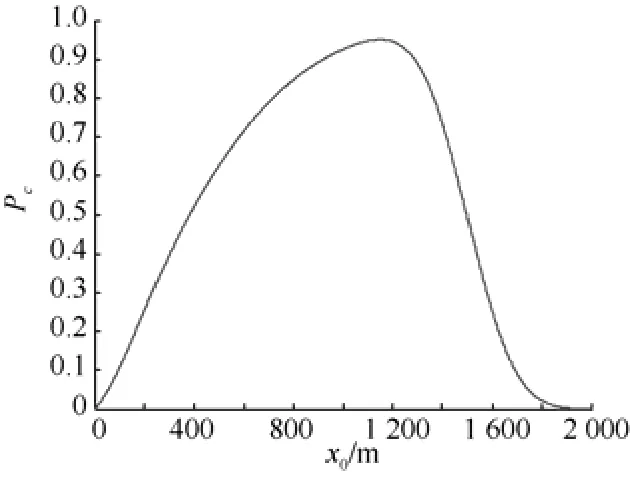
圖8　捕獲概率隨雷目距離的變化曲線Fig. 8　Curve of acquisition probability versus distance from ATT to target

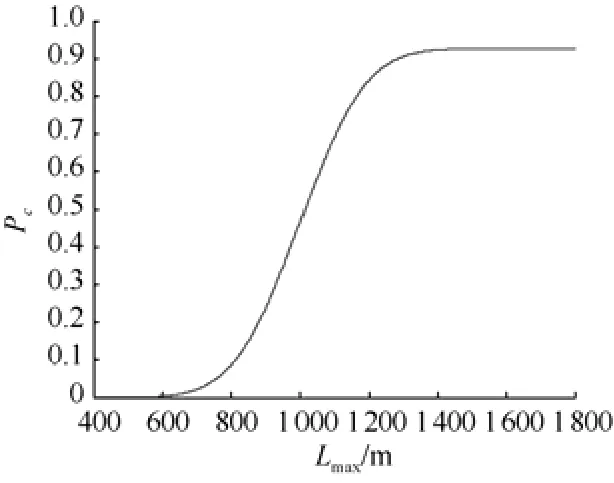
圖9　捕獲概率隨ATT自導頭的最大作用距離變化曲線Fig. 9　Curve of acquisition probability versus maximum operating range of homing head

圖10是捕獲概率Pc隨自導扇面角λ的變化曲線， 由圖可以看出， 捕獲概率Pc隨λ的增大而增大， 當λ＞35°時捕獲概率已接近1。

圖11是σx=150 m時捕獲概率Pc隨σz的變化曲線， 由圖可看出， 當σz＞1600 m時捕獲概率Pc已經(jīng)接近于0。圖12是σz=150 m時捕獲概率Pc隨σx的變化曲線， 由圖可看出， 當σx＞5 000 m 時捕獲概率Pc才接近于0。

這說明捕獲概率Pc隨著位置誤差的增大而減小， 但是隨著不同方向位置誤差增大而減小的幅度不同。其中， 視線方向的位置誤差σx對捕獲概率的影響較小， 而垂直于視線方向的位置誤差σz對捕獲概率的影響較大。在實際攔截中， 可以考慮把位置誤差最大的方向作為視線方向以降低誤差對捕獲概率的影響。

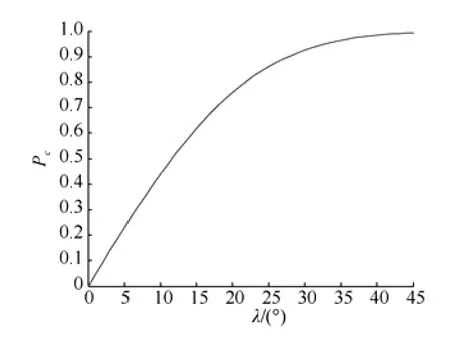
圖10　捕獲概率隨自導扇面角的變化曲線Fig. 10　Curve of acquisition probability versus homing sector angle

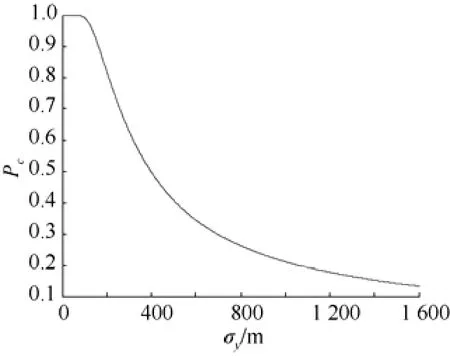
圖11　捕獲概率隨垂直于視線方向的位置誤差變化曲線Fig. 11　Curve of acquisition probability versus position error perpendicular to line of sight

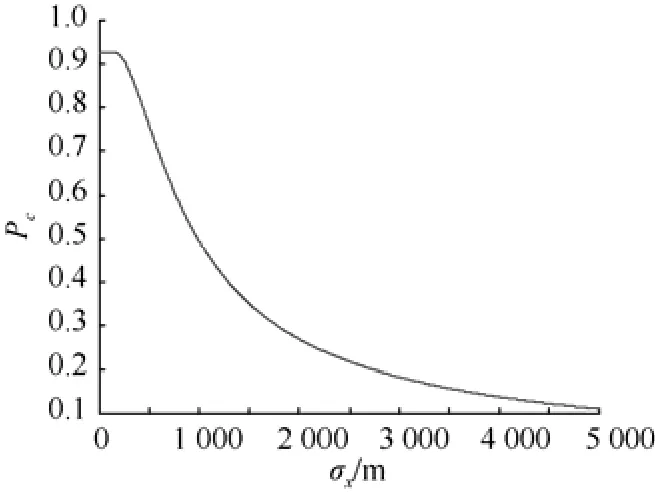
圖12　捕獲概率隨視線方向的位置誤差的變化曲線Fig. 12　Curve of acquisition probability versus position error along line of sight

4　結(jié)束語

文中首先分析了反魚雷魚雷末制導捕獲概率的定義， 將捕獲概率問題描述成ATT和來襲魚雷相對位置矢量落在一個扇形區(qū)域內(nèi)的概率問題；通過定義新的視線坐標系， 將捕獲概率的計算轉(zhuǎn)化為二維概率密度函數(shù)在扇形區(qū)域內(nèi)的積分； 利用積分區(qū)域近似法， 得到了一個簡潔的捕獲概率公式。仿真結(jié)果表明， 該近似算法精度高， 捕獲概率公式清楚地表明了彈目距離、導引頭最大自導作用距離、自導扇面角和位置誤差精度對捕獲概率的影響。文中所建立的捕獲概率模型可為反魚雷魚雷的彈道設(shè)計和作戰(zhàn)效能分析提供理論參考。

［1］ 陳敬軍. 國外反艦魚雷的現(xiàn)狀與發(fā)展趨勢［J］. 聲學技術(shù)， 2013， 32（2）： 164-170.

Chen Jing-jun. The Status Quo and Development Trend of Overseas Anti-surface Ship Torpedo［J］. Technical Acoustics， 2013， 32（2）： 164-170.

［2］ 楊緒升， 劉建兵， 周慶飛. 聲自導魚雷射擊諸元及誤差對其捕獲概率的影響［J］. 指揮控制與仿真， 2009， 31（5）：93-97.

Yang Xu-sheng， Liu Jian-bing， Zhou Qing-fei. Effect on Acoustic Homing Torpedo Capture Probability of Fire Elements and Errors［J］. Command Control & Simulation，2009， 31（5）： 93-97.

［3］ 張亞， 孔軍. 潛射巡航導彈現(xiàn)在點攻擊捕獲概率計算［J］. 指揮控制與仿真， 2010， 32（2）： 40-42， 45.

Zhang Ya， Kong Jun. Discussion on Catch-probability of Submarine-launched Cruise Missile′s Current-point Attack Mode［J］. Command Control & Simulation， 2010，32（2）： 40-42， 45.

［4］ 趙晶， 戴幻堯， 來慶福， 等. 自控終點誤差與目標散布下反艦導彈捕獲概率分析［J］. 戰(zhàn)術(shù)導彈技術(shù)， 2010（2）：64-68.

Zhao Jing， Dai Huan-yao， Lai Qing-fu， et al. Analysis of Acquisition Probability of Anti-ship Missile Under Auto-control Term Imation Error and Target Scattering［J］. Tactical Missile Technology， 2010（2）： 64-68.

［5］ 雷志東， 張曉林， 郭桂友. 遠程目標指示條件下的反艦導彈一次捕獲概率研究［J］. 戰(zhàn)術(shù)導彈技術(shù)， 2009（4）：59-63， 67.

Lei Zhi-dong， Zhang Xiao-lin， Guo Gui-you. Study of One-time Acquisition Probability of Anti-ship Missile Under Condition of Long Distance Target Indication［J］. Tactical Missile Technology， 2009（4）： 59-63， 67.

［6］ 盧燕， 舒?zhèn)髂? 蒙特卡洛法在導彈末制導雷達對目標的位置捕獲概率估計中的應(yīng)用［J］. 戰(zhàn)術(shù)導彈技術(shù)， 2005（1）：55-58， 65.

Lu Yan， Shu Chuan-mo. The Application of Monte Carlo Method to Estimation of Position Acquisition Probability of Terminal Guidance Radar［J］. Tactical Missile Technology， 2005（1）： 55-58， 65.

［7］ 曠志高， 劉鼎臣. 反艦導彈純方位發(fā)射捕捉概率計算方法［J］. 火力與指揮控制， 2003， 28（5）： 109-112.

Kuang Zhi-gao， Liu Ding-chen. Discussion on the Calculation Method of Catch Probability about Anti-ship Missile′s Passive Radar Concealed Attack［J］. Fire Control & Command Control， 2003， 28（5）： 109-112.

［8］ 魏海光， 邊聚廣. 一種反艦導彈純方位攻擊捕獲概率計算方法［J］. 四川兵工學報， 2012， 33（3）： 22-25.

［9］ 王軍， 谷良賢， 王博， 等. 毫米波制導導彈系統(tǒng)誤差及捕獲概率研究［J］. 航空計算技術(shù)， 2012， 42（5）： 25-27， 32.

Wang Jun， Gu Liang-xian， Wang Bo， et al. Research on System Error Analysis and Acquisition Probability of MMW Guide Weapon［J］. Aeronautical Computing Technique， 2012， 42（5）： 25-27， 32.

［10］ 谷志軍. 攔截機動目標末制導技術(shù)研究［D］. 長沙： 國防科學技術(shù)大學， 2009.

［11］ 明星， 陳喜， 蔣興舟. 雙雷齊射互導概率及目標捕獲概率研究［J］. 魚雷技術(shù)， 2006， 14（4）： 52-55.

Ming Xing， Chen Xi， Jiang Xing-zhou. Probability Calculation of Mutual-guiding and Target Acquisition under Two Torpedoes Salvo［J］. Torpedo Technology， 2006， 14（4）： 52-55.

［12］ 李敏勇， 蔣興舟. 網(wǎng)絡(luò)魚雷的實現(xiàn)和效能［J］. 魚雷技術(shù)，2003， 11（3）： 46-50.

［13］ 田恒斗， 曹慶剛， 侯代文， 等. 火箭助飛魚雷捕獲概率的解析模型［J］. 兵工學報， 2013， 34（7）： 916-921.

Tian Heng-dou， Cao Qing-gang， Hou Dai-wen， et al. Analytical Model of Rocket-assisted Torpedo′s Acquisition Probability［J］. Acta Armamentarii， 2013， 34（7）： 916-921.

［14］ 管賀， 孫學海， 薛昌友. 自導作用距離對主動聲自導魚雷捕獲概率的影響［C］//中國造船工程學會電子技術(shù)學術(shù)委員會2011年海戰(zhàn)場電子信息技術(shù)學術(shù)年會論文集.北京： 中國造船工程學會電子技術(shù)學術(shù)委員會， 2011：117-118， 157.

［15］ 馬國強. 主動自導魚雷多次連續(xù)捕獲概率的統(tǒng)計求解法［J］. 海軍工程學院學報， 1992， 17（1）： 76-82.

（責任編輯： 許妍）

Modeling and Simulation of Acquisition Probability Model for Terminal Guidance of Anti-Torpedo Torpedo

XIAO Cong-shan1，2，YANG Hui-zhen1，2
（1. School of Marine Science and Technology， Northwestern Polytechnical University， Xi′an 710072， China； 2. Science and Technology on Underwater Information and Control Laboratory， Xi′an 710075， China）

An analytical model of acquisition probability for terminal guidance of anti-torpedo torpedo （ATT） is established. Firstly， by considering the position error between an ATT and an incoming torpedo at the moment when midcourse guidance changes over to terminal guidance， the acquisition probability is described as an double integration of the probability density function in the domain determined by homing sector angle and homing range. The integration area is approximated to a rectangle. Then， an analytical expression of ATT′s acquisition probability， which relates to the position error between ATT and target， the distance from ATT to target， the ATT homing range， and the homing sector angle，is deduced. The effects of these four variables on ATT acquisition probability are analyzed quantitatively via simulation.

anti-torpedo torpedo； terminal guidance； acquisition probability； probability integral

TJ63

A

1673-1948（2015）06-0454-07

10.11993/j.issn.1673-1948.2015.06.012

2015-05-06；

2015-06-03.

國防科技重點實驗室基金（9140C230404130C23084）.

蕭叢杉（1992-）， 女， 在讀碩士， 主要研究方向為反魚雷魚雷制導技術(shù).