復M onge-Ampère方程Neumann邊值問題解的梯度估計①
向妮,王玉娥,石菊花
(湖北大學數學與統計學院,湖北 武漢 430062)
0 引言
復Monge-Ampère方程的研究問題源于多重位勢理論、微分幾何中的Calabi猜想和物理學等,該問題涉及多復變、微分幾何以及完全非線性偏微分方程等重要研究領域.該方程的Dirichlet邊值問題已有相當豐富的研究成果,而對于其Neumann邊值問題,李松鷹[1]得到了解的存在性、唯一性和正則性.對實Monge-Ampère方程的Neumann邊值問題,Lions等[2]證明了解的存在性,他們的證明中關于解的梯度估計由解的凸性就很容易得到.2014年,徐金菊[3]證明實Monge-Ampère方程的Neumann邊值問題梯度估計過程中也應用了解的凸性,然而對復情形而言,多重下調和函數沒有凸函數這樣的性質,因此解的梯度估計與二階導數估計難度相同,并且文獻[3]中的辦法并不適用.筆者將在后續工作中,努力改進文獻[3]中的辦法討論復Monge-Ampère方程Neumann邊值問題的梯度估計.
在文獻[1]中,作者直接證明了解的梯度估計.根據文獻[2]中的辦法,將整體約化到邊界,再分3種情形討論,直接得到解的梯度估計.而本文中,我們給出解的梯度估計一個新證明,先假設梯度估計存在,按照李松鷹[1]的思路重寫二階導數估計的證明,得到梯度估計與二階導數估計的關系,再利用插值不等式得到解的全局梯度估計.我們研究復Monge-Ampère方程的Neumann邊值問題:

其中Ω是Cn中有界光滑強擬凸域,ν為邊界外法向量,γ0>0,f≥f0>0,f∈C2(Ω),?∈C2(?Ω).另外,取λ1(z)為?Ω上曲率,記λ1=inf{λ1(z),z∈?Ω}.
定理1Ω是Cn中有界光滑強擬凸域是邊值問題(0.1)式與(0.2)式的多重下調和解.f≥f0>0,f∈C2(Ω),?∈C2(?Ω)且γ0+2λ1>0,γ0>0,則

其中C與相關 .
1 最大模估計與二階導數估計

其中Ω是Cn中的有界光滑強擬凸域,ν為邊界外法向量顯然可得
1.1 最大模估計為了文章的完整性,我們引用文獻[1]中關于最大模估計的結論:
引理1.1Ω是Cn中的有界強擬凸域,邊界是C1的,假設是(0.1)式與(0.2)式的多重下
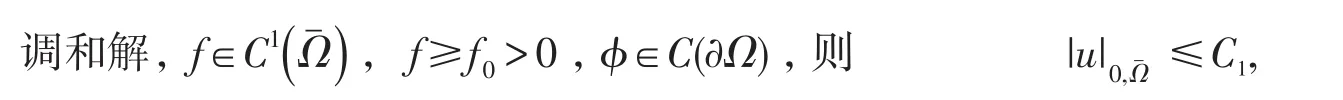
其中C1僅與相關.
1.2 二階導數估計本節中按照李松鷹在文獻[1]中的辦法重寫二階導數估計的證明.
定理2Ω是Cn中的有界強擬凸域,邊界是C3的.假設是(1.1)與(1.2)式的多重下調和
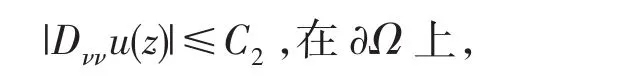
其中C2僅與相關,與M1無關.
定理2的證明為了保證證明的完整性,我們給出證明思路.
任取一點z0∈?Ω,由旋轉和平移,可以假設z0=0,則在0點附近的邊界定義函數
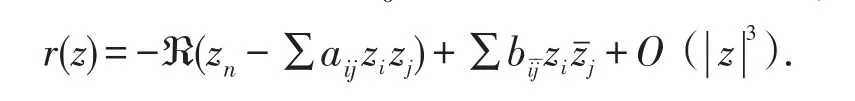
由于r是嚴格多重下調和函數,所以(biˉˉj)是正定矩陣.下面考慮邊值條件(1.2)式在全純變換后的形式,取新的坐標滿足:
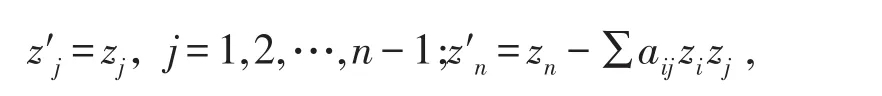
在此變換下,邊值條件不具備不變性.
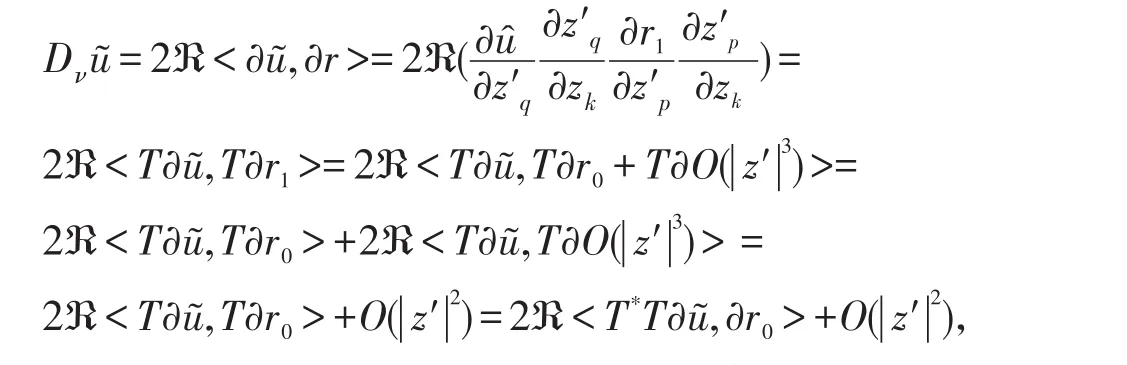
其中T=(?z′/?z)是變換z′=ψ(z)對應的Jacobian矩陣且|O(|z′|2)|≤C|z′|2,取
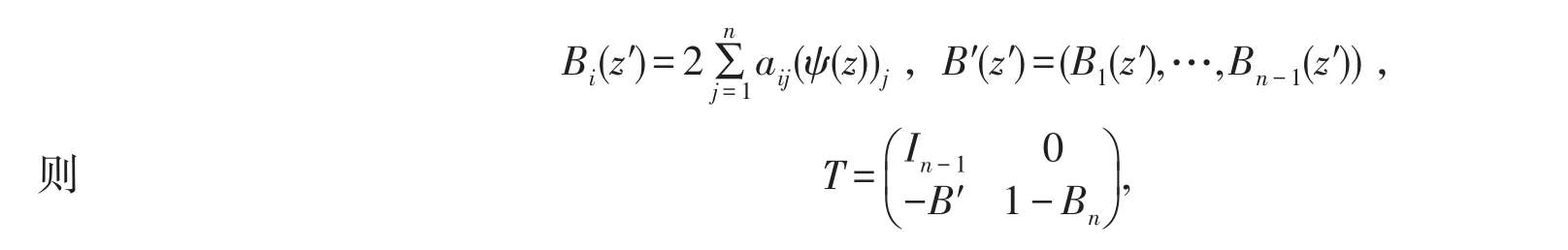
計算可得
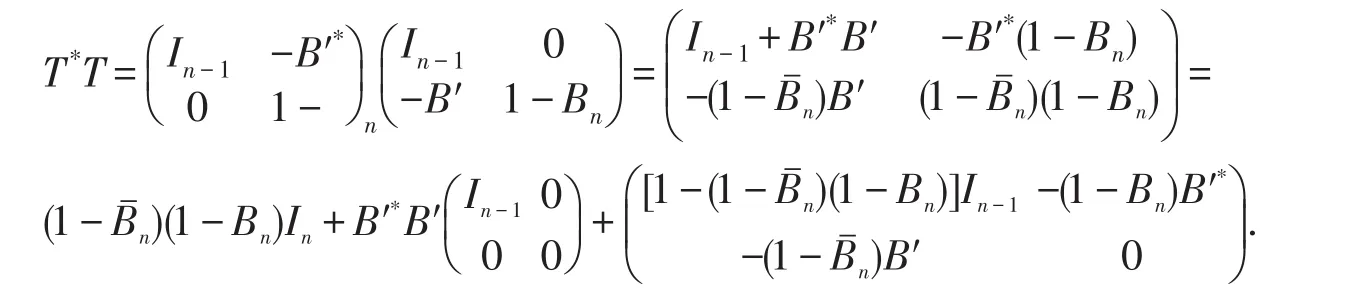
因為Bj=O(|z′|)且 ?r0/?z′j=O(|z′|),j<n, 所以


由復Monge-Ampère方程在全純變換下的性質可知,取則

為了方便,用z代替z′,u~代替u^,g代替g^,可知

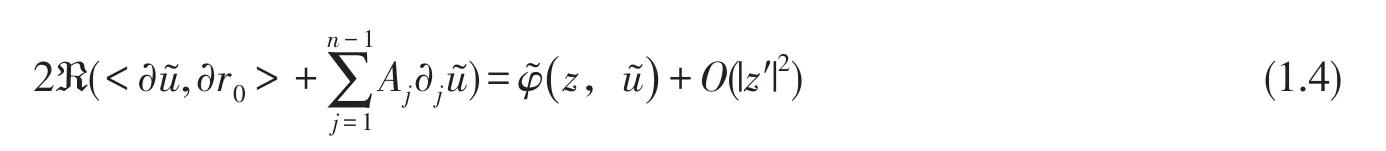
則Neumann邊值條件為:
考慮函數
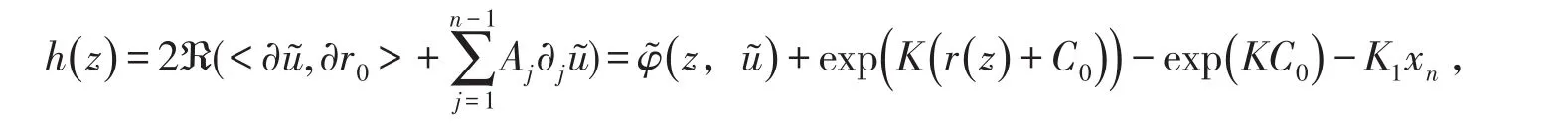
1)當K1=C/ε2足夠大時,在?(B(0 ,ε)?Ω)上有h(z)<0;
由1)、2)利用極大值原理可得,h只能在?(B(0 ,ε)?Ω)上取得其在B(0,ε)?Ω上的極大值,
3)在 ?Ω上取K1足夠大,則h在0處取得極大值,因此,0≤Dνh(0)≤即
定理3Ω是Cn中的有界強擬凸域,邊界是C3的是邊值問題(1.1)與(1.2)式的多重下調和解且γ0+2λ1>0,則

其中C4僅與相關,與M1無關.
定理3的證明在最大模估計和梯度估計存在的前提下,(1.5)式等價于

是多重下調和的,進一步地,可證(1.6)式等價于

考慮輔助函數

取τ為z點的切向量,ν為z點的外法向量,則通過下面的計算可知其中b(z),ak(z)均為Ω上的光滑函數.
V(z,ξ)作為(z,ξ)的函數應滿足:
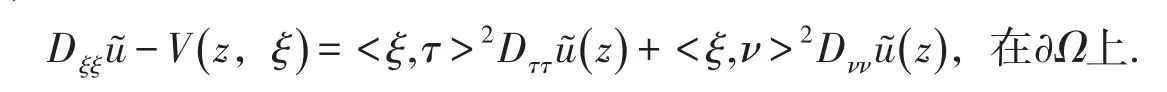
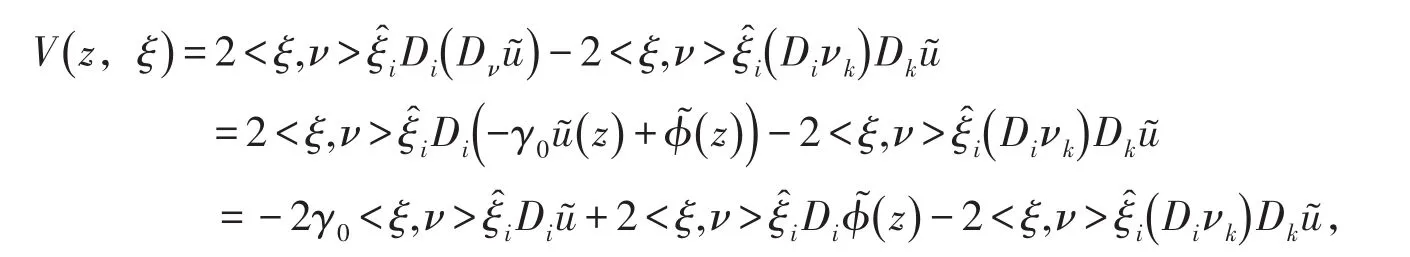
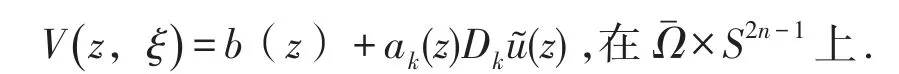
由V(z,ξ)的表達式可知,

下面分3種情況討論:
a)若ξ0是邊界上z0處的外法向量,則由定理3可知Dξ0ξ0u~≤C,則W(z0,ξ0)≤C2,從而可知,

b)若ξ0在z0點既不是切向量也不是法向量,則
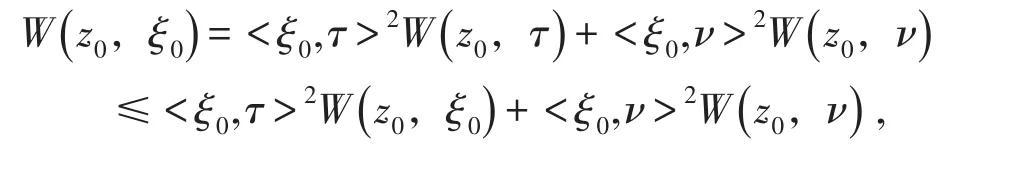
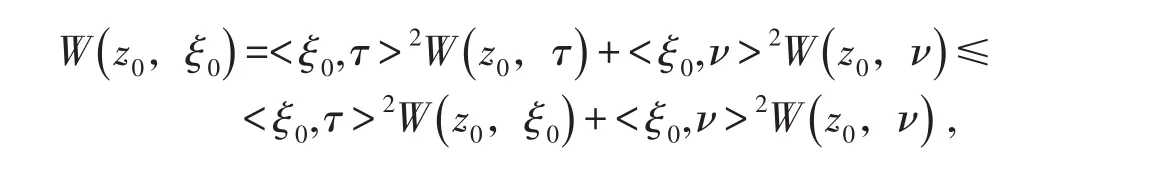
其中ξ0=<ξ0,τ>τ+<ξ0,ν>ν且<τ,ν>=0.于是由(a)知(1.7)式成立.
c)若ξ0是邊界上z0點處的切向量,則

取


不失一般性,假設z0∈?Ω點處外法向量是(0,…,0,1),則由于r是Ω上的強多重下調和定義函數且在?Ω上故H(z0,r)≥λ1Ⅰ2n-1且
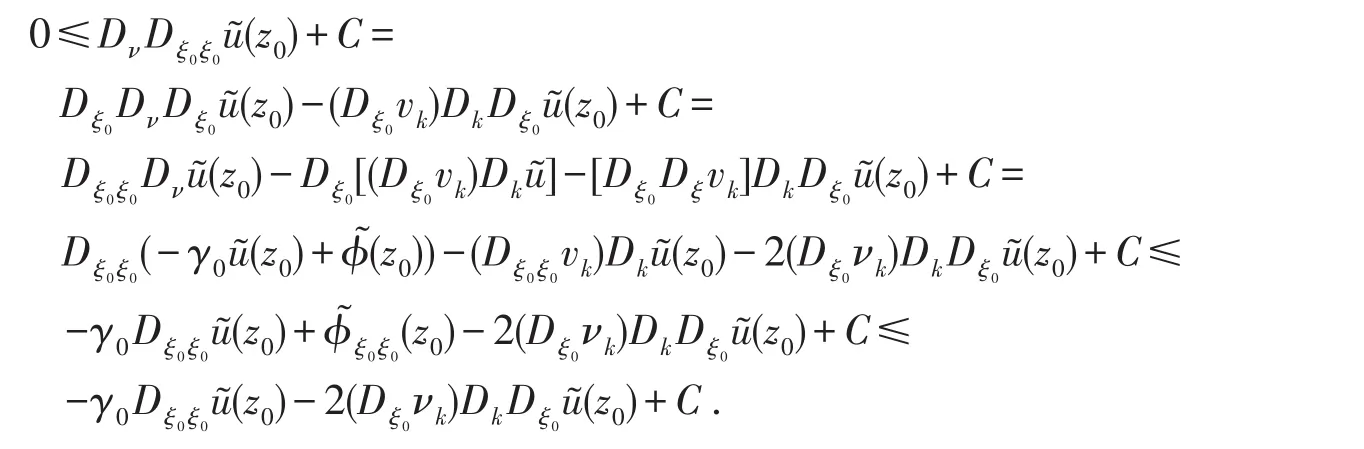
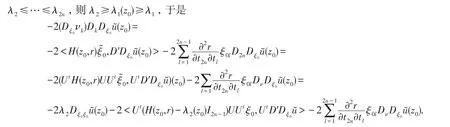
(H(z0,r)-λ2(z0)Ⅰ2n-1)是非負定矩陣,故成立.因此
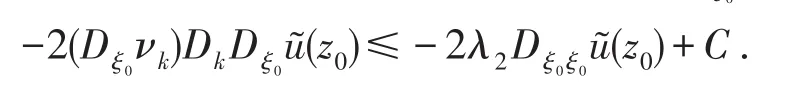

由a)中的結論可知,(1.7)式成立,則定理得證.
2 梯度估計
下面我們引入Gilbarg D等[4]有關Schauder理論中插值不等式引理6.35如下:
引理2.1假設j+β<k+α,其中j=0,1,2,…,k=1,2,…,0≤α,β≤ 1,Ω是 ?n中的Ck,α區域,假設則對任意的ε>0 及常數C=C(ε,j,k,Ω)使得

定理2.2Ω 是 ?n中的有界強擬凸域,邊界是C3的,u∈C4(Ω)?C3(Ωˉ)是邊值問題(1.1)與(1.2)的多重下調和解且γ0+2λ1>0,γ0>0,則
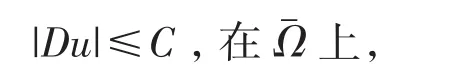
其中C僅與n,Ω,λ1,γ0,|?|2,Ωˉ,|f|2,Ωˉ相關.
定理2.2的證明由注3及引理2.1結論,利用插值不等式可知,
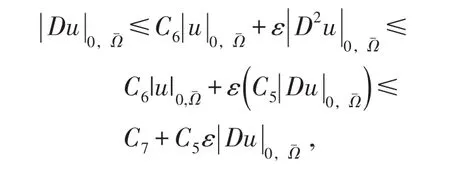
[1]LiSY.Boundary value problems for complex Monge-Ampère type[D].Pittsburgh:University of Pittsburgh,1992.
[2]Lions P L,Trudinger N S ,Urbas J IE.The Neumann problem for equations of Monge-Ampère type[J].Comm Pure Appl Math,1986,39:539-563.
[3]徐金菊.平均曲率方程Neumann問題的梯度估計[D].合肥:中國科學技術大學,2014.
[4]Gilbarg D.Trudinger NS.Elliptic partial differentiale quations of second order[M].2nd ed.NewYork:Springer-Verlag,1984.
[5]Bedford,Taylor BA.The Dirichletproblem for acomplex Monge-Ampère equation[J].Invent Math ,1976,37:1-44.
[6]Bedford.Variational properties of the complex Monge-Ampère equation ,I:The Dirichlet princinple[J].Duke Math J,1978,45:375-403.
[7]Bedford.Variational properties of the complex Monge-Ampère equation,II:Intrinsic[J].A-mer JMath,1979,101:1131-1166.[8]Caffarelli L,Kohn JJ,Nirenberg L,et al.The Dirichlet problem for nonlinear second-order elliptic equations,II:Complex Monge-Ampère,and uniform ly elliptic equations[J].Comm Pure and Appl Math,1985,38:209-252.
[9]LiSY.On the Neumann problems for complex Monge-Ampère Equations[J].Indiana University Mathematics Journal,1994,43(4):1099-1122.

