多孔隙介質參數識別的正則化模擬退火法①
王迎
(黑龍江工業學院機電工程學院,黑龍江雞西158100)
隨著科學技術的飛速發展和人們生活水平的不斷提高,世界范圍內面臨著油氣資源需耗量大幅增加的趨勢,而現有的油氣資源是有限的,如果不去進一步勘察探尋油氣資源的分布,那么勢必會經受資源急劇短缺的嚴峻問題.可見,資源勘探技術尤為重要,其中涉及到在介質的波動方程中識別參數的問題.研究人員在勘探資源之前需要預先知道一些參數,諸如孔隙率、飽和度等來還原對應的介質波動方程,以此來預測所研究區域的地質層面結構,而要預知這些參數,就要通過參數識別方法來完成[1].另外,所勘探的地層通常是多孔介質,更接近真實的地層介質,因此其研究更具有實際意義[2].本文中有效結合了具有全局收斂特性的模擬退火法以及求解非適定問題的正則化方法,形成了二維多孔隙介質波動方程的參數孔隙率識別問題的正則化-模擬退火算法.
1 參數識別模型
描述二維多孔隙介質波動方程的模型為
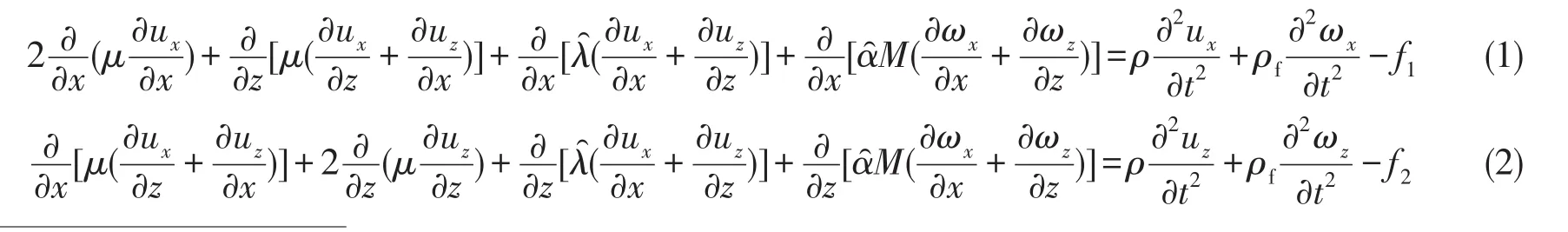

固體和流體物質的物理參數及各個參數間的關系如下所示,這些參數均為關于x和z的變量.
Kb:骨架體變模量;ρs:固體密度;Gb:骨架切變模量;m:有效流體密度;Ks:固體體變模量;ρf:液體密度;λb:固體骨架的Láme系數;λ?:雙相介質的Láme系數;μ:孔隙介質的切變模量;Kf:液體體變模量;β:孔隙率;α?、M:飽和多孔隙介質壓縮性系數,且系數滿足
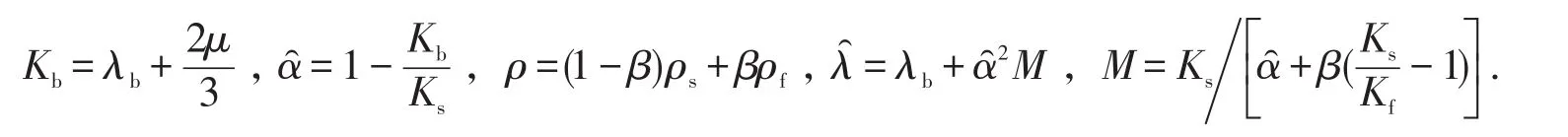
邊界條件:
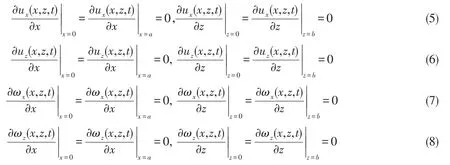
初始條件:
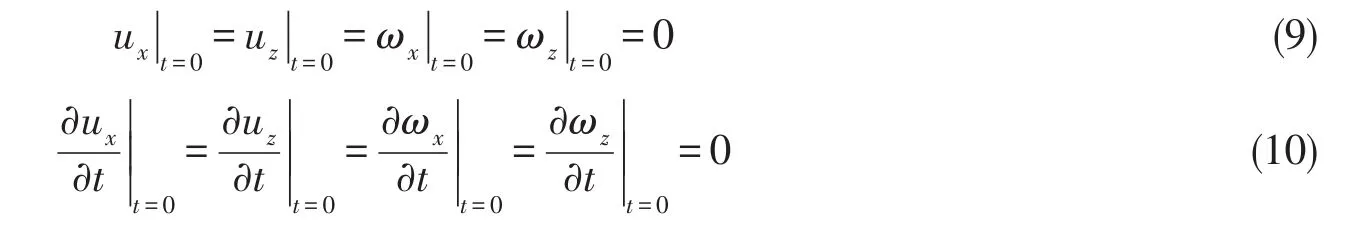
(1)~(10)式構成了二維雙相介質波動方程的正問題模型,即由已知孔隙率β(x,z)可以求解出u(x,z,t).若孔隙率β(x,z)未知,給出附加條件

若對二維雙相介質波動方程(1)~(4)式考慮平行波入射時,f=g(t)δ(x),其中g(t)為震源函數,δ(x)為δ函數,且滿足g(t)=0,t<0,則(1)~(11)式就構成了二維多孔隙介質波動方程一般意義下的參數識別問題.
2 模型的離散化與參數識別算法
2.1 離散化模型設即分別為沿x,z方向的步長,τ為時間步長,記對方程(1)~(11)進行差分離散.為了簡單方便,將離散結果統一記作(12)式.
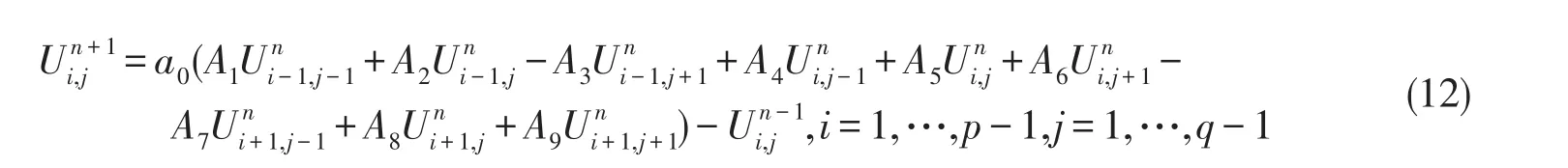
其中
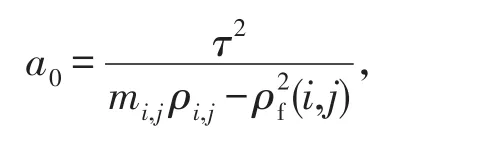
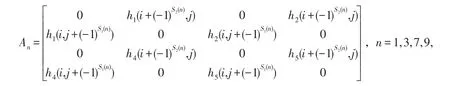
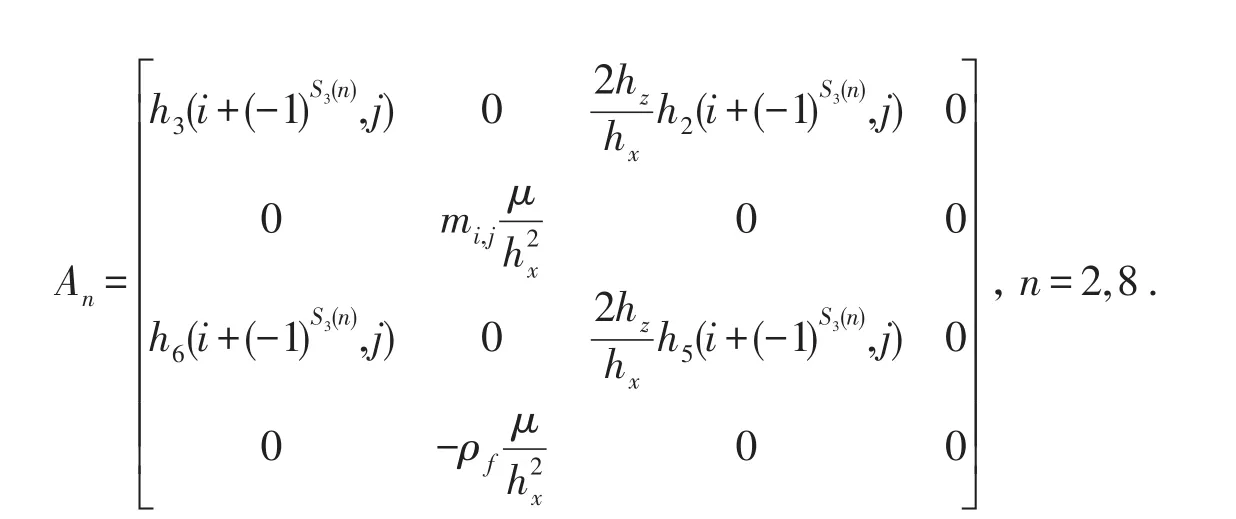


其中


2.2 參數識別的算法記
對β(i,j)及分別按適當順序排列,可排列成向量形式,分別記為B,G.
令
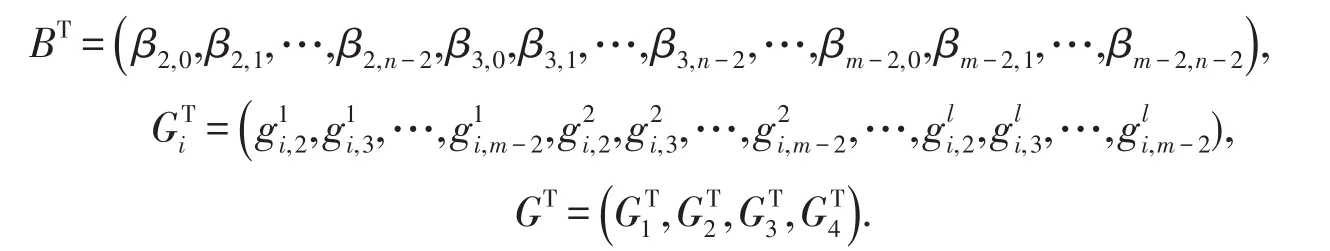
由(12)式定義了一個非線性向量值函數A:B→G.假設已知也進行對應排列,組成向
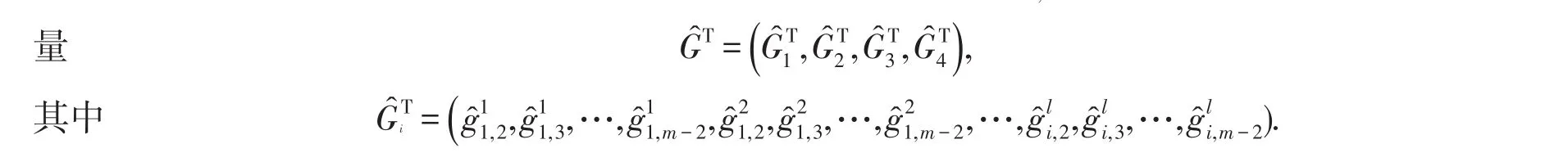
于是反演βi,j的問題轉化成求解泛函

的非線性優化問題.
為了克服反問題的不適定性,進而達到數值求解的穩定性,利用正則化方法在(13)式中引入光滑泛函,獲得泛函

其中,α為正則化參數,M1、M2分別為x方向、z方向的二階光滑矩陣[4].
通過求解滿足下式的最優解B*,將要求解的二維流體飽和多孔隙介質波動方程反問題再次轉化為求解非線性優化問題

Jα(B)的梯度為
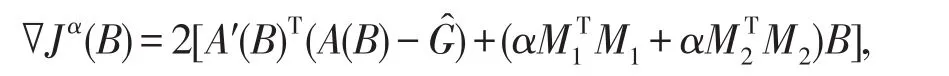
其中,A′(B)是A(B)關于B的Jacobi矩陣.
模擬退火法作為隨機化算法[4]的通用方法之一,主要思想是通過設置隨機迭代函數來產生隨機解,最終在有限時間內搜尋到符合終止條件的最優解.根據所研究的問題給出一個初始猜測值B0,通過(16)式迭代產生B1,B2,….我們期望存在一個Bk是(15)式的解或者存在某一收斂于解的點列.

其中c為產生擾動的系數,rand(q+1,p+1)為隨機數矩陣.
在上述模型的基礎上,結合正則化方法,得到多孔隙介質波動方程反演的正則化模擬退火算法,其算法流程為:
步驟1:給定初始溫度T0,初始點B0為對應階初值矩陣,及ε>0,正則化參數α>0,k?0.
否則,如果k+1=N,則Tn+1=σTn,B0?Bk+1,k?0,轉步驟2;
否則,轉步驟4.
步驟 4:計算 Δm=Jα(Bk+1)-Jα(Bk),
若Δm<0,則Bk=Bk+1,k?k+1,轉步驟2;
否則,轉步驟2.
上述算法中的kB=1.380 7×10-23J·K-1為Boltzmann常數,rand( )q+1,p+1為隨機數矩陣,c為產生擾動的系數,Δm為目標函數之差(評價函數的增量),σ為指數降溫的系數,N為B的維數.我們可以用圖1簡要描述此算法流程:

圖1 正則化模擬退火法流程圖
3 數值模擬
數值模擬使用形式為g(t)=sin(2πvt)exp(-2πvt)的雷克子波,其中入射波的頻率v取為75Hz.研究區域取為水平方向距離為260m、豎直方向為260m的區域,即a=260,b=260.在進行有限差分離散時,取水平差分步長為hx=10m,豎直差分步長為hz=10m,接收器在地表的每個差分點上.正則化參數α=0.000 95,相對誤差ε=1%,T0=1 050,c=1.5,σ=0.85,τ=0.002 s,參數識別時取孔隙率的初始值B0為所有元素都是0.2的相應階矩陣.
所選模型如圖1所示,它是一種異常體,其中兩塊具有尖點,其相應的各介質參數如表1所示.

表1 多孔隙介質模型的參數表
假設背景介質的孔隙率的精確值為0.4,位于上方的異常體內的孔隙率的精確值為0.25,位于下方的異常體內的孔隙率的精確值為0.3.對此模型使用正則化-模擬退火算法進行反演得到的結果如圖2所示.
4 結論
基于全局收斂的模擬退火方法與求解不適定性問題的正則化方法的思想,將兩者有機結合構造了正則化-模擬退火算法.為增加參數識別的收斂性和穩定性,利用此算法識別二維多孔隙介質波動方程的參數孔隙率.數值模擬的結果顯示出此算法能克服一般的參數識別方法的局部收斂性,能有效地解決具有非適定性、非線性性質的參數識別問題.

圖1 孔隙率模型

圖2 正則化模擬退火算法對孔隙率模型的參數識別結果
[1]王立榮.反問題的數值解法[D].深圳:哈爾濱工業大學深圳研究生院,2011.
[2]田迎春,章梓茂,趙成剛,等.黏彈性流體飽和孔隙介質動力反應分析的顯式有限元法[J].科學技術與工程,2010,10(5):1112-1112.
[3]張新明,劉克安,劉家琦.流體飽和多孔隙介質波動方程多尺度反演[J].應用力學學報,2007,24(1):87-90.
[4]黃鋒振,袁艷,張修寶,等.基于模擬退火的傅里葉變換成像光譜儀干涉圖相位修正[J].光譜學與光譜分析,2011,31(7):2012-2012.

