改進的復制動態方程及其穩定性分析

吳克晴，馮興來

（江西理工大學理學院，江西 贛州　341000）

改進的復制動態方程及其穩定性分析

吳克晴，馮興來

（江西理工大學理學院，江西 贛州341000）

針對原復制動態建立過程的缺陷，通過引入強度系數，使博弈參與者采取不同策略時更顯得相互依賴，體現出不同策略被采用的變化情況，擴展了進化博弈論的框架.針對均有兩個策略的兩個博弈參與者，研究分析了擴展后復制動態的穩定性，對以后科學管理具有重要指導意義.

進化博弈；復制動態；強度系數；進化穩定策略

1　引言

進化博弈理論的思想起源于達爾文的生物進化理論和拉馬克的遺傳基因理論［1］，視博弈參與者為有限理性，以群體為研究對象，其兩個基本的概念是進化穩定策略［2］和復制動態方程［3］，前者強調的是變異，后者強調的是選擇，由于變異后仍需要選擇，所以建立策略隨時間的總體動態非常關鍵，然而在運用進化博弈理論時，專家學者廣泛采用文獻［3］中的復制動態方程：其思想是選擇某一特定策略頻率的變化就等于該策略的適應度與群體平均適應度之間的差值，這種做法雖然克服了學習能力弱的個體在無法用“最優反應動態”模擬策略［4］選擇時的困惑，然而并未考慮同一群體下策略間的相互依賴情況.

2　復制動態的構造

對于一群體A，假設存在n1種狀態，且在t時刻第i（i=1，2，···，n1）種狀態下小群體的數量為mi（t），生存適應能力為ui（t），所占群體A的比率為xi（t），t時刻群體A的平均生存適應度為

3　復制動態的進化分析

多個群體的復制動態的進化穩定性分析，可以從對兩個群體兩種選擇狀態的穩定性分析開始.本節就兩種選擇狀態的兩個群體展開其穩定性分析.

假設有兩個博弈參與者A和B，均存在兩種選擇狀態，其收益矩陣如表1.

表1兩個博弈參與者A和B的收益矩陣

上表中a，b，c，d，e，f，g，h表示各博弈狀態下的值；x1（t）與x2（t）分別表示t時刻A在第一、第二種狀態下的數量所占A的比例；y1（t）與y2（t）分別為t時刻B在第一、第二種狀態下的數量所占B的比例；λ1與λ2分別表示A在第一、第二種狀態下的數量的自然增長率；ρ1與ρ2分別表示B在第一、第二種狀態下的數量的自然增長率.

假設u1（t）與u2（t）分別表示t時刻A在第一、第二種狀態下的收益；ˉu為t時刻A的平均收益；w1（t）與w2（t）分別表示t時刻B在第一、第二種狀態下的收益；ˉw為t時刻B的平均收益，則

系統（5）的平衡點［6］的穩定性可通過文獻［7］中提供的方法判別，即當系統（5）的雅可比矩陣的行列式為正值，其跡為負值時，平衡點是穩定的；行列式為正值，跡為正值時，平衡點是不穩定的；當行列式為負值時，跡為任意值時，平衡點為鞍點.由于參數值的大小未定，所以trJ 與detJ的符號未定，從而影響平衡點的穩定性，此分析過程略，現將所有的分析結果列舉如下：

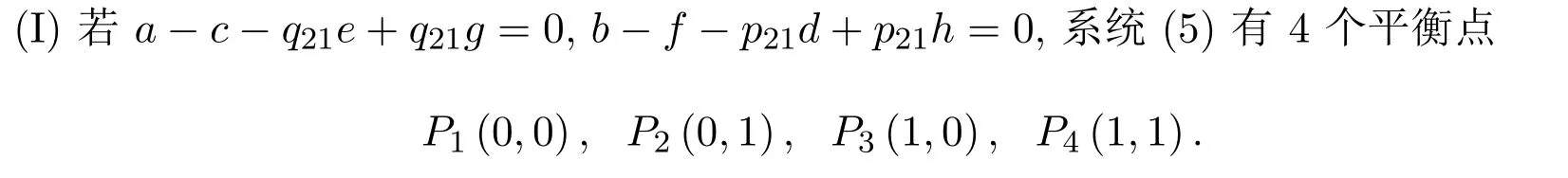
此時所有的分析結果為：

（1）當a-q21e＜0，f-p21h＜0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為不穩定點；

（2）當a-q21e＜0，f-p21h＞0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點；

（3）當 a-q21e＞0，f-p21h＜0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為不穩定點，P3（1，0）為穩定點；

（4）當 a-q21e＞0，f-p21h＞0時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為穩定點.

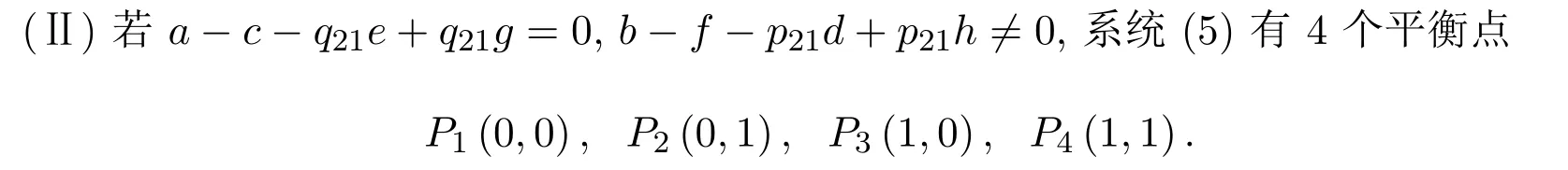
此時所有的分析結果為：

（1）當a-q21e＜0，b-p21d＜0，f-p21h＜0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為不穩定點；

（2）當a-q21e＜0，b-p21d＞0，f-p21h＜0時，P1（0，0）為穩定點，P2（0，1）、P4（1，1）為鞍點，P3（1，0）為不穩定點；

（3）當a-q21e＜0，b-p21d＜0，f-p21h＞0時，P1（0，0）、P3（1，0）為鞍點，P2（0，1）為穩定點，P4（1，1）為不穩定點；

（4）當a-q21e＜0，b-p21d＞0，f-p21h＞0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點；

（5）當a-q21e＞0，b-p21d＜0，f-p21h＞0時，P1（0，0）為不穩定點，P2（0，1）、P4（1，1）為鞍點，P3（1，0）為穩定點；

（6）當a-q21e＞0，b-p21d＜0，f-p21h＜0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為不穩定點，P3（1，0）為穩定點；

（7）當a-q21e＞0，b-p21d＞0，f-p21h＞0時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為穩定點；

（8）當a-q21e＞0，b-p21d＞0，f-p21h＜0時，P1（0，0）、P3（1，0）為鞍點，P2（0，1）為不穩定點，P4（1，1）為穩定點.

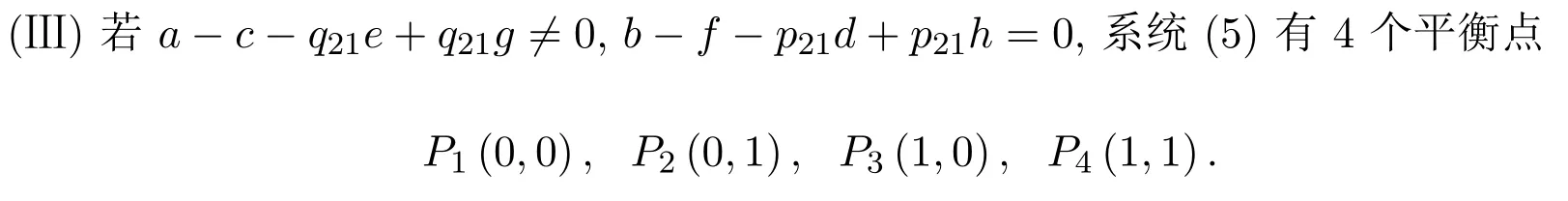
此時所有的分析結果為：

（1）當a-q21e＞0，c-q21g＜0，f-p21h＜0時，P1（0，0）為穩定點，P2（0，1）為不穩定點，P3（1，0）、P4（1，1）為鞍點；

（2）當a-q21e＜0，c-q21g＜0，f-p21h＜0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為不穩定點；

（3）當a-q21e＜0，c-q21g＞0，f-p21h＞0時，P1（0，0）為不穩定點，P3（1，0）、P4（1，1）為鞍點，P2（0，1）為穩定點；

（4）當a-q21e＜0，c-q21g＜0，f-p21h＞0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點；

（5）當a-q21e＞0，c-q21g＞0，f-p21h＜0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為不穩定點，P3（1，0）為穩定點；

（6）當a-q21e＜0，c-q21g＞0，f-p21h＜0時，P1（0，0）、P2（0，1）為鞍點，P3（1，0）為穩定點，P4（1，1）為不穩定點；

（7）當a-q21e＞0，c-q21g＞0，f-p21h＞0時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為穩定點；

（8）當a-q21e＞0，c-q21g＜0，f-p21h＞0時，P1（0，0）、P2（0，1）為鞍點，P3（1，0）為不穩定點，P4（1，1）為穩定點.

此時，需分以下幾種情形進行討論.

（1）當 a-q21e＜ c-q21g＜ 0，b-p21d＜ f-p21h＜ 0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0）、P5（x?，y?）為鞍點，P4（1，1）為不穩定點；

（2）當 0＜c-q21g＜a-q21e，0＜f-p21h＜b-p21d時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0）、P5（x?，y?）為鞍點，P4（1，1）為穩定點；

（3）當 0＜c-q21g＜a-q21e，b-p21d＜f-p21h＜0時，P1（0，0）、P4（1，1）為鞍點、P2（0，1）為不穩定點，P3（1，0）為穩定點，P5（x?，y?）為中心點；

（4）當a-q21e＜c-q21g＜0，0＜f-p21h＜b-p21d時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點，P5（x?，y?）為中心點.

（1）當 0＜c-q21g＜a-q21e，b-p21d＜0＜f-p21h時，P1（0，0）為不穩定點，P2（0，1）、P4（1，1）、P5（x?，y?）為鞍點，P3（1，0）為穩定點；

（2）當 a-q21e＜ c-q21g＜ 0，f-p21h＜ 0＜ b-p21d時，P1（0，0）為穩定點，P2（0，1）、P4（1，1）、P5（x?，y?）為鞍點，P3（1，0）為不穩定點；

（3）當a-q21e＜c-q21g＜0，b-p21d＜0＜f-p21h時，P1（0，0）、P3（1，0）為鞍點，P2（0，1）為穩定點，P4（1，1）為不穩定點，P5（x?，y?）為中心點；

（4）當0＜c-q21g＜a-q21e，f-p21h＜0＜b-p21d時，P1（0，0）、P3（1，0）為鞍點，P2（0，1）為不穩定點，P4（1，1）為穩定點，P5（x?，y?）為中心點.

（1）當 0＜c-q21g＜a-q21e，0＜b-p21d＜f-p21h時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為穩定點，P5（x?，y?）為中心點；

（2）當a-q21e＜c-q21g＜0，0＜b-p21d＜f-p21h時，P1（0，0）、P4（1，1）、P5（x?，y?）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點；

（3）當0＜c-q21g＜a-q21e，f-p21h＜b-p21d＜0時，P1（0，0）、P4（1，1）、P5（x?，y?）為鞍點，P2（0，1）為不穩定點，P3（1，0）為穩定點；

（4）當 a-q21e＜ c-q21g＜ 0，f-p21h＜ b-p21d＜ 0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為不穩定點，P5（x?，y?）為中心點.

（1）當a-q21e＜0＜c-q21g，0＜f-p21h＜b-p21d時，P1（0，0）為不穩定點，P2（0，1）為穩定點，P3（1，0）、P4（1，1）、P5（x?，y?）為鞍點；

（2）當c-q21g＜0＜a-q21e，0＜f-p21h＜b-p21d時，P1（0，0）、P2（0，1）為鞍點，P3（1，0）為不穩定點，P4（1，1）為穩定點，P5（x?，y?）為中心點；

（3）當c-q21g＜0＜a-q21e，b-p21d＜f-p21h＜0時，P1（0，0）為穩定點，P2（0，1）為不穩定點，P3（1，0）、P4（1，1）、P5（x?，y?）為鞍點；

（4）當a-q21e＜0＜c-q21g，b-p21d＜f-p21h＜0時，P1（0，0）、P2（0，1）為鞍點，P3（1，0）為穩定點，P4（1，1）為不穩定點，P5（x?，y?）為中心點.

（1）當a-q21e＜0＜c-q21g，f-p21h＜0＜b-p21d時，P1（0，0）、P4（1，1）為不穩定點，P2（0，1）、P3（1，0）為穩定點，P5（x?，y?）為鞍點；

（2）當c-q21g＜0＜a-q21e，b-p21d＜0＜f-p21h時，P1（0，0）、P4（1，1）為穩定點，P2（0，1）、P3（1，0）為不穩定點，P5（x?，y?）為鞍點；

（3）當c-q21g＜0＜a-q21e，f-p21h＜0＜b-p21d時，P1（0，0）、P2（0，1）、P3（1，0），P4（1，1）為鞍點，P5（x?，y?）為中心點；

（4）當a-q21e＜0＜c-q21g，b-p21d＜0＜f-p21h時，P1（0，0）、P2（0，1）、P3（1，0），P4（1，1）為鞍點，P5（x?，y?）為中心點.

（1）當a-q21e＜0＜c-q21g，0＜b-p21d＜f-p21h時，P1（0，0）為不穩定點，P2（0，1）為穩定點，P3（1，0）、P4（1，1）為鞍點，P5（x?，y?）為中心點；

（2）當c-q21g＜0＜a-q21e，f-p21h＜b-p21d＜0時，P1（0，0）為穩定點，P2（0，1）為不穩定點，P3（1，0）、P4（1，1）為鞍點，P5（x?，y?）為中心點；

（3）當c-q21g＜0＜a-q21e，0＜b-p21d＜f-p21h時，P1（0，0）、P2（0，1）、P5（x?，y?）為鞍點，P3（1，0）為不穩定點，P4（1，1）為穩定點；

（4）當a-q21e＜0＜c-q21g，f-p21h＜b-p21d＜0時，P1（0，0）、P2（0，1）、P5（x?，y?）為鞍點，P3（1，0）為穩定點，P4（1，1）為不穩定點.

（1）當 0＜a-q21e＜c-q21g，0＜f-p21h＜b-p21d時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為穩定點，P5（x?，y?）為中心點；

（2）當 c-q21g＜ a-q21e＜ 0，b-p21d＜ f-p21h＜ 0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0）為鞍點，P4（1，1）為不穩定點，P5（x?，y?）為中心點；

（3）當c-q21g＜a-q21e＜0，0＜f-p21h＜b-p21d時，P1（0，0）、P4（1，1）、P5（x?，y?）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點；

（4）當0＜a-q21e＜c-q21g，b-p21d＜f-p21h＜0時，P1（0，0）、P4（1，1）、P5（x?，y?）為鞍點，P2（0，1）為不穩定點，P3（1，0）為穩定點.

（1）當 0＜a-q21e＜c-q21g，b-p21d＜0＜f-p21h時，P1（0，0）為不穩定點，P2（0，1）、P4（1，1）為鞍點，P3（1，0）為穩定點，P5（x?，y?）為中心點；

（2）當 c-q21g＜ a-q21e＜ 0，f-p21h＜ 0＜ b-p21d時，P1（0，0）為穩定點，P2（0，1）、P4（1，1）為鞍點，P3（1，0）為不穩定點，P5（x?，y?）為中心點；

（3）當c-q21g＜a-q21e＜0，b-p21d＜0＜f-p21h時，P1（0，0）、P3（1，0）、P5（x?，y?）為鞍點，P2（0，1）為穩定點，P4（1，1）為不穩定點；

（4）當0＜a-q21e＜c-q21g，f-p21h＜0＜b-p21d時，P1（0，0）、P3（1，0）、P5（x?，y?）為鞍點，P2（0，1）為不穩定點，P4（1，1）為穩定點；

（1）當 0＜a-q21e＜c-q21g，0＜b-p21d＜f-p21h時，P1（0，0）為不穩定點，P2（0，1）、P3（1，0），P5（x?，y?）為鞍點，P4（1，1）為穩定點；

（2）當 c-q21g＜ a-q21e＜ 0，f-p21h＜ b-p21d＜ 0時，P1（0，0）為穩定點，P2（0，1）、P3（1，0），P5（x?，y?）為鞍點，P4（1，1）為不穩定點；

（3）當c-q21g＜a-q21e＜0，0＜b-p21d＜f-p21h時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為穩定點，P3（1，0）為不穩定點，P5（x?，y?）為中心點.

（4）當0＜a-q21e＜c-q21g，f-p21h＜b-p21d＜0時，P1（0，0）、P4（1，1）為鞍點，P2（0，1）為不穩定點，P3（1，0）為穩定點，P5（x?，y?）為中心點.

4　進一步分析

根據以上分析，當收益矩陣中參數值滿足（I）或（II）或（III）的時，系統（5）有4個平衡點

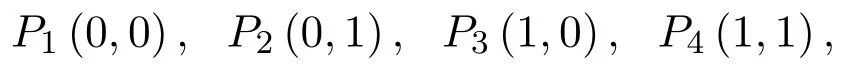
隨著時間推移，最終的穩態平衡點唯一，且該平衡點的進化與強度系數λi，ρi（i=1，2）有關；但當收益矩陣中參數值滿足（Ⅳ）時，系統（5）有5個平衡點

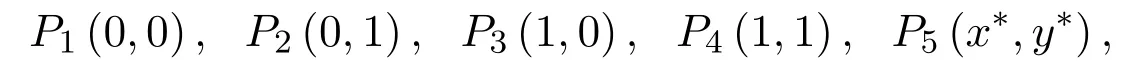
經過時間進化最終可能沒有穩態平衡點或穩態平衡點不一定唯一（如（Ⅳ）下的情形5），而對于兩個穩態平衡點中偏向哪一個的程度或處于中心點偏向哪一個狀態的程度也與強度系數λi，ρi（i=1，2）有關，下面不妨以（Ⅳ）下情形5中（1）的情況進行分析，其它情況可類似.

（Ⅳ）情形5中（1）的情況：當

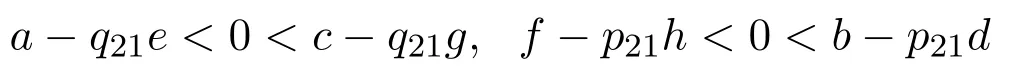
時，P1（0，0），P4（1，1）為不穩定點，P2（0，1），P3（1，0）為穩定點，P5（x?，y?）為鞍點.此時，系統的動態演化圖［8-9］如圖1所示.

在此情況下，顯然P5（x?，y?）為以P1（0，0），P3（1，0），P4（1，1），P2（0，1）為頂點組成的四邊形中的一個內部點.

根據幾何圖形及相關知識，由P1（0，0），P3（1，0），P4（1，1），P5（x?，y?）為頂點圍成的四邊形區域面積S為：

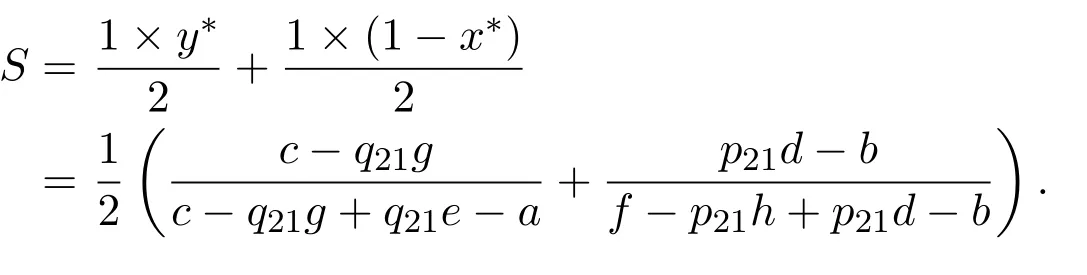
由于

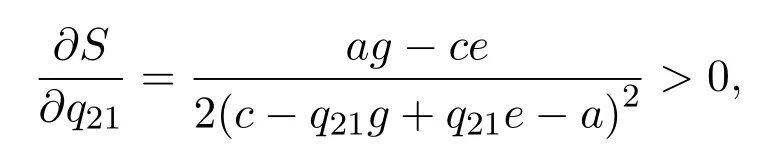
所以當增加q21時，S會增大，即當博弈參與者A在兩種狀態下增長率λ2與λ1的比值q21越大，其均衡策略為x1（t）=1.

同理，由于

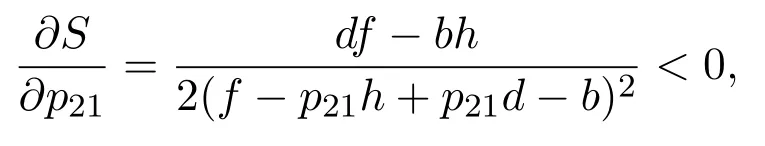
所以當增加p21時，S會減少，即當博弈參與者B兩種狀態下增長率ρ2與ρ1的比值p21越大，其均衡策略為y1（t）=0，從而系統（5）的穩定狀態更趨于平衡點P3（1，0），反之，系統（5）的穩定狀態更趨于平衡點P2（0，1）.

圖1當a-q21e＜0＜c-q21g，f-p21h＜0＜b-p21d時的動態演化圖

5　結語

本文通過引入強度系數，擴展了文獻［3］中的進化博弈論框架.并針對兩個策略的兩個博弈參與者的情形，分析了他們采取不同策略時的進化穩定性情況，反映出強度系數對博弈決策的影響；最后，進一步研究表明了強度系數影響參與者在多個穩態下最終的優化行為，即影響動態系統穩定狀態的演變趨勢.

可以看到，雖然本文局限于分析兩個策略的兩個博弈參與者的情形，但對于多個博弈參與者多種策略的穩定狀態，類似可得到研究.即方程（5）解的穩定狀態分析對方程（3）解的穩定狀態分析具有基礎作用，僅計算量相對較為復雜.這對以后利用進化博弈理論，來解決分析實際問題具有重要的指導作用.

［1］殷輝，陳勁，謝芳.開放式創新下產學合作的演化博弈分析［J］.情報雜志，2012，31（9）：185-190.

［2］Smith J M.Evolution and the Theory of Games［M］.New York：Cambridge University Press，1982.

［3］Taylor P D，Jonker L B.Evolutionary stable strategies and game dynamics［J］.Mathematical Bioscience，1978，40：145-156.

［4］劉偉兵，王先甲.進化博弈決策機制設計綜述［M］.運籌與管理，2008，17（1）：84-87.

［5］趙瓊，別群益.一類修正的 Holling-Tanner捕食模型的持久性和全局漸近穩定性 ［J］.數學的實踐與認識，2013，43（18）：292-298.

［6］何德明，何萬生，謝保利.一類具有線性收獲率的生物捕食系統的定性分析 ［J］.純粹數學與應用數學，2013，29（1）：33-39.

［7］郭軍華，李幫義，倪明.雙寡頭再制造進入決策的演化博弈分析［J］.系統工程理論與實踐，2013，33（2）：330-377.

［8］王磊，張慶普.基于慣例視角的高校科研團隊創造力演化博弈分析［J］.科學學與科學技術管理，2012，33（8）：82-90.

［9］梅強，馬國建，杜建國，等.中小企業安全生產管制路徑演化研究［J］.中國管理科學，2009，17（2）：160-168.

Improved replicated dynamic equations and its stability analysis

Wu Keqing，Feng Xinglai

（College of Science，Jiangxi University of Science and Technology，Ganzhou341000，China）

Based on the defects from the original replicated dynamic establishment，different strategies adopted are made more interdependent for game players by introducing strength coefficient，the changes of different strategies adopted are better reflected，and the framework of evolutionary game theory is extended.For two game players with two strategies，the stability of the replicated dynamics improved is analyzed.As a result，the analysis obtained in this paper has important guiding significance for scientific management.

evolutionary game，replicated dynamic，strength coefficient，evolutionarily stable strategy

O225；F224.32

A

1008-5513（2015）03-0221-10

10.3969/j.issn.1008-5513.2015.03.001

2014-02-20.

國家自然科學基金（61364015，61064006）.

吳克晴（1972-），博士，副教授，研究方向：運籌學、泛函分析.

2010 MSC：91A22，93C15