運算律應該怎么教學
俞正強

不管是學生還是教師,都覺得運用乘法分配律很難,差錯很多,因此,有許多學生很怕簡便運算。這很令教師困惑:原本可以減輕計算負擔的運算定律為何卻成為學生的負擔?下面我們以“乘法分配律”為例,討論運算律應該怎么教學。
一、理解:算律是算法的“竅門”
計算教學的目標可以概括為四個字:又對又快。當將算律與算法放在一起時,相對而言,算法解決的是“對”的問題,而算律解決的是“快”的問題。算律是對算法的熟能生“竅”。因此,算律源于算法的運用。所以,算律的教學應該從算法的運用開始。為此,“乘法分配律”的教學應該有這樣的流程。
流程一:練習,看誰算得又快又對。(獨立完成)
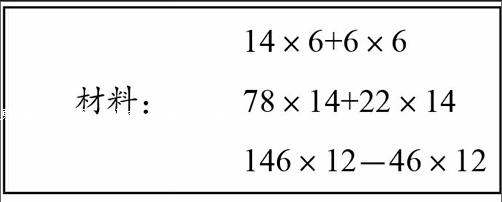
14×6+6×6
78×14+22×14
146×12– 46×12
……
設計意圖:這些題目,學生在計算時會有以下兩種方法。
方法1:按照“先乘除后加減”的算法進行計算
14×6+6×6
=84+36
=120
方法2:按照“幾個幾加幾個幾一共幾個幾”的意義理解進行計算
14×6+6×6
=20×6
=120
就當下的學生而言,對混合運算的算法,教師是教過的。但運用乘法意義來做這題目,則是學生自己的“調皮”,或者說是“竅門”。
流程二:討論,怎樣算得又對又快?
問題:我們能改變運算順序嗎?
結論:14個6加6個6一共是20個6。
設計意圖:學生對乘法分配律的理解,在小學二年級算兩位數乘一位數的時候,就已經蘊含其中了。
12×3→10×3+2×3=36
當時的理解是10個3加2個3一共是12個3。因此,學生理解14個6加6個6是20個6是很自然的事。也就是說,學生將這一類題目的運算順序加以改變,十分自然。
流程三:討論,我們改變運算順序跟這些題目有關嗎?是不是所有題目都可以改變運算順序呢?
材料: 14×6+6×6
78×14+22×14
146×12-46×12
結論:運算特征: 乘 加(減) 乘 a×b±c×b
數字特征:有一個相同數 b
兩個湊整數 a±c為一整數
設計意圖:教師提供的這組練習題有兩個特征:運算特征與數字特征。當滿足這兩個特征時,可以先加減后乘,這樣就把運算律的前提條件給明確了。
流程四:判斷這樣算法,是又對又快嗎?
① (25+14)×4 ② (15+45)×3
=25×4+14×4 =15×3+45×3
=100+56 =45+135
=156 =180
問題1:先算括號里面再算括號外面,這兩道題目都沒有先算括號里面,可以嗎?
問題2:改變運算順序的目的是什么?哪道題目的算法滿足這個目的?
設計意圖:幾個幾加幾個幾等于共有幾個幾,反之,共有幾個幾可以分為幾個幾加幾個幾。改變運算順序的目的是為了又對又快,于是得出我們認可并推薦的“竅門”,將其命名為乘法分配律。
(a±b)c=ac±bc
流程五:練習(略)
二、討論:算律是“規律”的運用
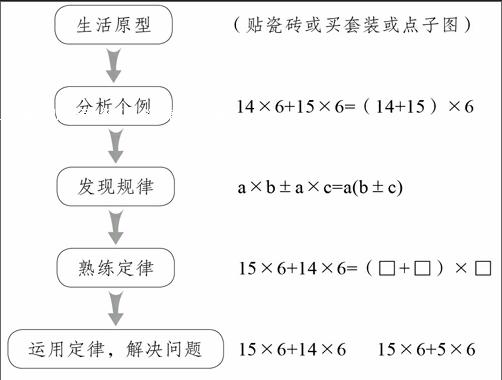
目前,教材基本上把算律歸為“規律”,其基本流程如下。
與該流程相類似的在小學數學教學中通常限于“數學好玩”或“數學廣角”等材料中,比如“打電話”。
我們可以比較打電話與乘法分配律兩個教學內容,打電話需要分析個例發現規律,以解決比較繁雜的問題,這是正確的。但乘法分配律這個算律如果稱之為規律,可以用意義來理解,不需要發現。把乘法分配律作為問題解決來教學,是在把簡單問題復雜化。
三、推而廣之:加法交換律應該怎么教學
一次,有位同事問:加法交換律的生活原型是什么?想了許久,也想不出加法交換律的原型。在去聽課的過程中,發現有的教師會請兩位學生到講臺上來,問其他學生:這是誰和誰?
然后將兩位學生交換位置,問:這又是誰和誰?
學生回答:是誰和誰。
教師問:有沒有變化?
學生回答:沒有變。
教師又說:這是不是說明位置變了,大小沒變啊?
學生回答:是的。
聽了這個原型,心里有一種說不出的味道,書上是這樣設計的:
一問:2+8=10
二問:8+2=10
三問:同學們,有什么發現嗎?
問題是,2+8=8+2,這需要發現嗎?難道不發現就不能知道2+8=8+2了嗎?
那么,正確的呢?自然應從算法入手。
流程一:練習,看誰算得又對又快?
8+6+2
7+9+3
11+5+9
流程二:交流,誰算得又對又快?
從左到右依次計算→先湊整再相加。
流程三:討論,這樣改變運算順序的理由是什么?
都是合并(加法意義)。
流程四:結論,連加算式中,如果能湊整,可以改變順序,交換位置,即兩個加數交換位置,和不變。
四、比較:差別在哪里
我們來比較兩種教學流程所呈現的教學意義上的差別,如表1所示。
表1 兩種教學流程呈現的教學意義上的差別
兩種主張:對于知識而言,學生最終要記住ab±ac=a(b±c),并運用它以達到簡便運算的目的,差別不大。但對知識的獲得過程,兩種主張的差別是巨大的。
本文主張要使學生深刻地認識到,算律脫胎于對算法的靈活運用,而靈活運用的依據是對運算意義的理解。教材主張的特征是割裂了算律與算法之間的密切聯系,使之成為一個獨立于算法的規律,把一個自然而然的“竅門”變成隆重的問題解決。
以上思考,僅供大家參考。
(責任編輯:孫建輝)

