衛星數不足條件下GPS/SINS數據融合工程化算法

王 楠，周本川，程海彬

(中航工業空空導彈研究院，河南洛陽 471000)

GPS/INS組合導航系統已廣泛應用于飛行器、車載系統等領域，GPS/INS數據融合的原理是利用GPS提供的觀測信息估計INS的導航或器件誤差并對其進行校正，GPS接收機需要觀測4顆以上衛星才能進行導航定位，但是在GPS受到干擾或遮擋時，觀測衛星數可能只有2～3顆，這種情況下，傳統的基于GPS定位結果的GPS/INS組合導航模型由于GPS接收機失效而無法進行數據融合導航，并完全依賴INS導航系統。

事實上GPS衛星數目不足4顆條件下，GPS仍有可用信息，對輔助定位或定位推測有很大作用。為了解決2～3顆衛星條件下的GPS/INS數據融合問題，人們一般采用改進的數據融合方法或更高階次的系統模型，典型的方法有:“速度位置組合+鐘差聯合外推方法”［1］，“速度位置組合+構建第三方觀測量方法”［2-3］，“基于偽距偽距率的緊組合導航模型”［4］等方法。這些方法都能一定程度上解決2～3顆衛星條件下的GPS/INS數據融合問題，但也存在著諸如設備成本增加，精度難以保證，系統階次高計算耗時等弊端。

本研究提出一種在衛星數不完備條件下的工程化的數據融合方法，能夠克服傳統緊組合濾波算法在2～3顆衛星條件下的不足，具有實現簡單，可靠性高等特點。

1 現有方法及其不足

接收機鐘鐘差可采用類似GPS衛星鐘鐘差的二次多項式進行擬合［3］。常見的鐘差擬合公式為

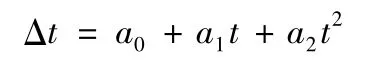
在正常衛星數不少于4顆時，利用單點定位獲得接收機鐘差，然后利用數個歷元的鐘差求解擬合系數a0，a1，a2。當運動載體進入遮擋環境觀測衛星數小于4顆時，利用前面正常定位條件計算出的鐘差系數外推接收機鐘差，因此衛星觀測方程只有3個未知的坐標參數，僅需觀測3顆衛星即可進行導航定位。

該方法缺點是鐘差漂移建模不準確，接收機的鐘的穩定度一般為 10 ～8 s［5］，并存在鐘差跳變的情況［6］;此外，鐘差的擬合系數估值也存在誤差，因此在短時間內鐘差外推精度可以接受，長時間遞推誤差隨時間增長很快。

2 速度位置組合+構建第三方觀測量

此類方法主要通過增加額外傳感器觀測信息來克服衛星數目不足4顆情況下可用方程數目不足的問題，常見的方法有引入里程計、磁力計、高度表、地圖匹配或高精度INS等附加運動約束。

除了GPS提供的直接觀測信息外，根據載體具體的運動環境、觀測條件等，系統中某些參數滿足一些特定的條件。這些運動信息充分利用相當于在觀測模型中增加了虛擬觀測信息，對解決組合系統觀測信息不足，部分參數難以準確估計的問題是有利的。

這些共同特點是增加硬件結構，增加成本，或者應用范圍有限，不便于工程化應用。

3 基于偽距/偽距率的緊組合方法

該方法是目前見諸文獻最多的方法，是目前此類問題的通用方法。原理是利用可用衛星測量的偽距和偽距率信息，把載體SINS的積累誤差映射成載體至衛星的視距誤差，通過kalman濾波對SINS的誤差進行濾波修正。系統狀態階數和量測方程數目較多，計算過程比較耗時。

該方法準確性受建模影響較大，模型誤差嚴重時可能造成相反方向修正的結果。誤差修正效果不能完全保證。原因在于:

觀測誤差向導航坐標系投影的大小取決于濾波器中各方向誤差的方差估計(即P矩陣)，P矩陣體現的是濾波器對當前誤差的評價，而通常情況下誤差的估計與實際誤差并不完全一致。這樣觀測誤差在導航系各方向的投影可能與該方向的實際誤差不一致，會出現總的合成誤差在收斂，而某一特定方向的誤差可能出現波動，即收斂過程中誤差可能先增大后減小的情況。如果在誤差處于較大的時間點上，衛星接收機定位中斷，那么該方向較大的誤差會一直保持，可能會對載體導航造成不可接受的影響。

4 工程化新算法

當衛星數僅為2～3顆時，接收機已不能給出速度位置的定位結果，但是能夠給出2～3顆衛星的偽距和偽距率測量值，因此該算法就是最大限度地利用這幾顆衛星的偽距和偽距率信息，校正理論上能夠觀測到并消除的誤差。

4.1 GPS偽距/偽距率測量方程

衛星定位接收機測量得到的與第j顆衛星之間的偽距可以表示為

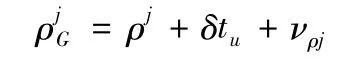
其中:ρj為理想距離;δtu為等效時鐘誤差相應的距離。由于δtu是偽距測量中的主要誤差，因此在建立偽距測量模型時，主要考慮了該項誤差的影響。νρj為偽距測量噪聲，由多路徑效應、對流層延遲誤差、電流層誤差等引起。可以近似認為是白噪聲，則慣導計算的載體位置(xIyIzI)與第j顆衛星之間的偽距為

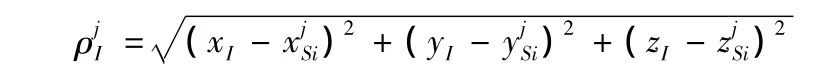
設(x y z)為載體和衛星之間的真實距離。(δxδyδz)為慣導計算的載體在導航坐標系的誤差。即

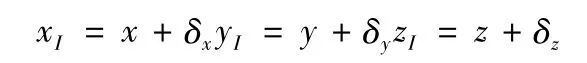
將計算式在(x y z)處進行泰勒展開，并忽略高階項可以得到:

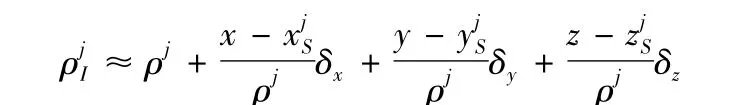
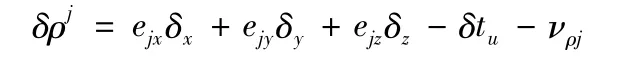
其中:δtu為接收機鐘差引起的偽距測量誤差;νρj表示包括多路徑，電離層延遲誤差在內的測量噪聲。

同理系統偽距率量測誤差方程為

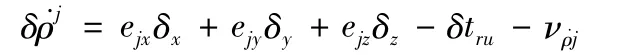
當衛星數為3顆時，以偽距觀測方程為例，能夠構造一個觀測方程組為

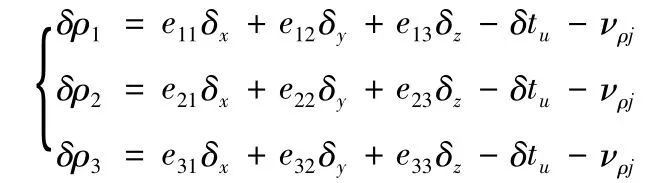
將其做線性變化后，可以將公共接收機鐘差δtu項消除，得到如下形式的方程組

4.2 誤差解算方法

上述方程組3個未知數兩個方程是存在無窮多個解的，但觀察方程組形式可以發現，形如Ax+By+Cz+D=0的方程在解析幾何上表示的是空間的一個平面，兩個這樣的平面相交，表示的是空間的一條直線，如將待估計的狀態(δxδyδz)T看作是以(0，0，0)為原點的一個空間向量，則該向量必定指向該空間直線上的某一點，具體指向哪一點，由于方程數量限制，是無法觀測到的。

誤差修正的根本目的是將誤差向量(δxδyδz)T消除，如確實不能完全消除，則應盡可能將其減少到最小，因此雖然(δxδyδz)T不能求解，但可以精確解出原點到空間直線的垂線向量，并將該向量作為誤差消除;顯然消除該垂線向量后，剩余不可消除的誤差部分其實就是原誤差在空間直線上的投影，屬于不可觀測的維度。且剩余的誤差一定小于原有誤差，即該方法誤差修正的方向一定是正確的。由于該方法僅從幾何關系上求解誤差，因此不會出現前文所述方法中存在的因模型不準確而造成誤差估算錯誤的情況。

點 P(x0，y0，z0)到空間直線 L

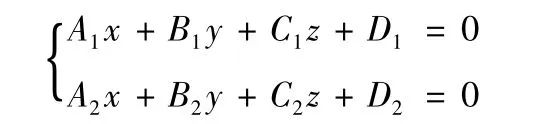
的距離公式為(證明過程參見文獻［7］):

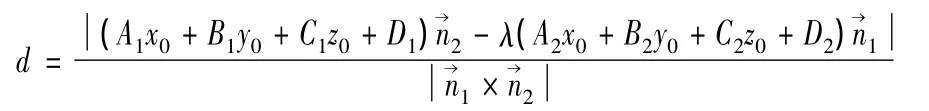
根據該距離公式即可求解出垂線方向上的誤差分量，可以用來修正慣導誤差。實際應用中可以經過低通濾波器以消除高頻噪聲。

2顆衛星情況下與此類似，線性變化后的觀測方程由2個變為1個，即:

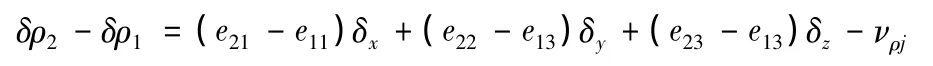
同理，可以精確解出原點到空間平面的垂線向量，并將該向量作為誤差消除;顯然消除該垂線向量后，剩余不可消除的誤差部分其實就是原誤差在空間平面上的投影，屬于不可觀測的維度(且是2個維度不可觀測);且剩余的誤差一定小于原有誤差，誤差修正的方向也一定是正確的。

點 P(x0，y0，z0)到空間直線

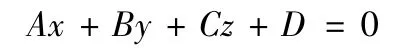
的距離公式為(證明過程參見文獻［7］)

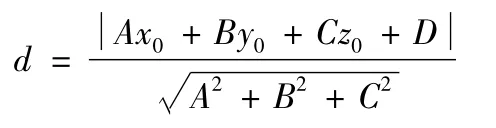
根據該距離公式即可求解出垂線方向上的誤差分量，可以用來修正慣導誤差。實際應用中可以經過低通濾波器以消除高頻噪聲。

5 仿真結果

下面給出仿真驗證結果，仿真條件為:采用SINS/GPS組合導航方式，SINS初始速度誤差北天東3個方向均為3 m/s，位置初始誤差3個方向均為0 m，初始姿態誤差設為0，仿真驗證純慣性導航、2～3顆衛星下導航、以及衛星正常定位狀態下導航的速度位置誤差收斂趨勢，結果如圖1～圖2所示。

圖1 速度誤差

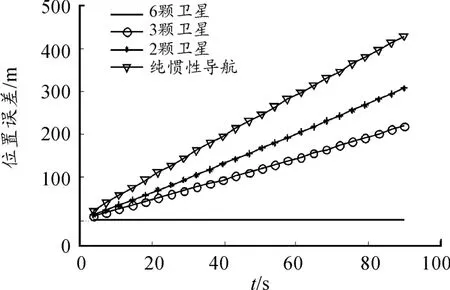
圖2 位置誤差

由仿真結果可以看出，2～3顆星情況下，該算法能夠將一半以上的速度和位置誤差消除(能消除多少還與3顆衛星的分布有重要關系，沒有固定指標，理論上0% ～100%都有可能，由觀測幾何關系確定)。且3顆星情況下略好與2顆衛星情況，這2顆衛星取的是這3顆衛星中的2顆，與上文的推斷符合，因此印證該算法是可行的。

6 結論

針對GPS接收機觀測衛星數不足4顆條件下的GPS/SINS數據融合問題，對目前常見的解決方法進行了綜述，分析了現有方法的優缺點，并一種新的算法以克服現有算法不足，該算法根據可見衛星的偽距/偽距率信息，利用幾何關系，將慣導誤差在觀測方向的投影消除，僅殘留部分不可觀測的誤差，將誤差修正到理論上的最小值。仿真測試結果良好，2～3顆星條件下組合精度相對衛星數大于4顆的情況會有所下降，組合后精度與衛星視線方向與慣導誤差矢量的夾角有關，但明顯高于純慣導精度。

［1］甘雨，隋立芬.GPS/SINS緊組合導航中接收機鐘差建模［J］.大地測量與地球動力學，2014，34(6):50-54.

［2］柴艷菊，陽仁貴.附加運動約束提高 GPS/INS導航參數估計精度［J］.中國慣性技術學報，2011，19(1):28-32.

［3］林雪原，何友.GPS/羅蘭C/SINS/AHRS組合導航系統［J］.電子科技大學學報，2008，37(1):4-7.

［4］王楠，王龍.慣性系下GPS/SINS緊組合導航算法研究［J］.現代電子技術，2011，34(20):93-96.

［5］楊龍，徐冬梅，張守信，等.關于北斗衛星導航系統的被動式定位算法比較研究［J］.空間科學學報，2006，26(3):203-208.

［6］李永利.點到平面距離公式的簡證及相關結論［J］.高等數學研究，2005，8(2):27-29.

［7］李志明，李宏偉.距離問題的垂足法求解［J］.高等數學研究，2010，13(2):41-43.