華北地區強震的等待時間研究

孫麗娜 齊玉妍 金學申

河北省地震局，石家莊市槐中路262號 050021

0 引言

強震的孕育、發生是極其復雜的物理過程，離上次發生強震的時間越長，離下一次地震的時間不一定也越長。Garavaglia等(2007)的工作指出，如果考慮強震的發生只取決于從上一強震之后的若干時間發生，那么在某區域的地震預測是可能的。

假設某地區在某時間發生了一次強震，對于如何判斷下一次地震的發生時間，許多研究者從不同的角度對不同環節提出了各種有益的探索。然而，就地震復發模型而言至今仍主要沿用泊松過程的假定。當去除余震后，小地震活動符合泊松分布(Gardner et al，1974)，而在一個較大范圍里的中強地震活動在時間軸上卻遵從成叢分布(Knopoff et al，1996)。按照這個假設，周期性的地震活動遵從有限的成叢性，可以精確地預測。一般來說，如果有時間上的聚集性，且在已有地震時間分布的前提下，那么就可以計算未來一定時間間隔的發震概率。為了定量描述這一性質，我們把在給定區域自上一次強震以來的持續時間與在給定時間間隔范圍內的強震發生的條件概率聯系起來，計算強震在給定時間的發生概率。

本文從概率論的原理出發，推導出計算強震等待時間的公式，然后依據各分布模型，得到等待時間的計算公式，在此基礎上，計算了河北省及鄰近地區的5.0級以上強震等待時間的概率。

1 下一次地震的等待時間

假定P(t)是地震時間間隔的概率密度，而t是自上一次地震以來的時間，t'是從現在到下一次地震發生的時間間隔，即等待時間(Sornette et al，1997)。現在的問題是要求得t'的概率密度函數P(t')。據貝葉斯條件概率公式

我們假定P(A)=P(t+t')，這就是從現在開始到下一次地震發生時的時間間隔為t'的概率。同時假定也就是從上一次地震發生到現在沒有地震發生的概率。這樣，歸一化的條件概率公式為

建筑施工總包商和分包商的實際經濟、技術實力仍存在著較大差異，針對這一情況，建筑施工單位各部門應對此建立合理有效的施工技術管理體系，對于傳統的建筑施工技術管理體系進行轉型，建立和健全施工技術管理體系，形成專業部門從而管理施工技術工作，保證在分包時，建筑施工單位要落實管理責任工作，將責任落實到各個部門。另外，施工企業在工程施工過程中，應做好各部門的協調工作，調整工作人員調動，發揮工作人員的自身優勢，做到人盡其才，加強各部門在施工過程中的配合工作，使各部門相互協助完成工作，進而在保證工程質量的前提下提高施工效率。同時，施工企業單位要重視施工人員業務素質能力，定期對施工人員進行職業素質培訓。

由(2)式得平均等待時間為

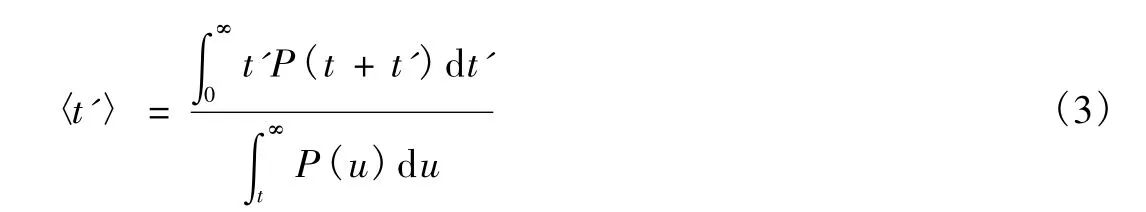
通過簡單的變量變換u=t+t'，可以得到

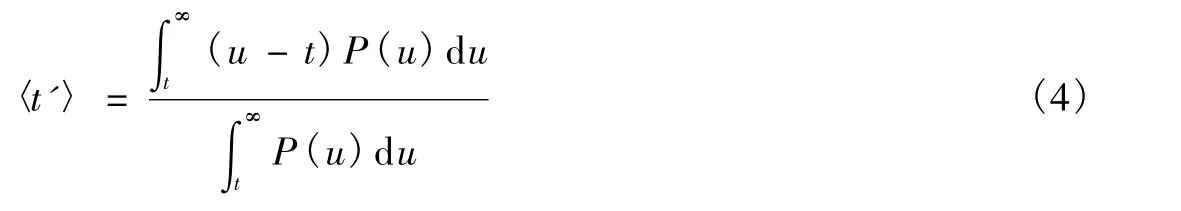
由分部積分，得到

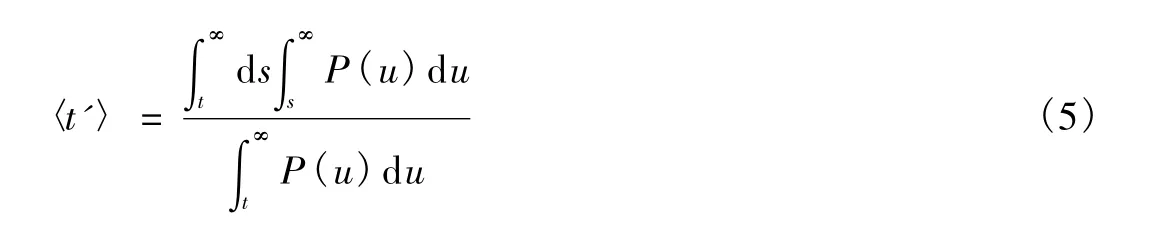
為簡單起見，把(5)式寫成

f(t)是p(u)的二重積分，因此有

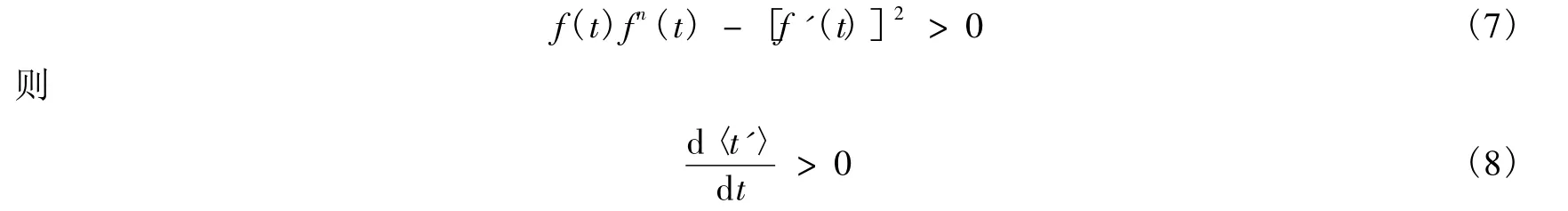
同樣，設f(t)=e－g(t)，如果g″(t)＜0，則如果P(t)在t=0時有限，我們也能發現(5)式的變換形式，這對等待時間短的情況十分有用。因為對短的等待時間，有積分結果可以直接據(5)式得到:〈t〉是兩地震間的平均重復時間，設其中τ是等待時間的估計值，它是根據上一次地震以來的時間估計得到的。我們把它看作為t'的瞬時估計。這樣就可以寫成

如果瞬時估計τ小于平均的等待時間，那么，到下一次地震的時間隨著離逝時間的增加而增加，這表明平均等待時間反應的是整個時間中各部分的貢獻。而如果〈t〉的值大于τ，則表明這是在非零時刻大于τ的那部分的貢獻。在這種情況下，如果〈t〉小于τ，離下一次地震的時間隨著離逝時間的增加而減少。在特殊情況下，如果P(0)=0，則離下一次地震的時間隨著離逝時間的增加而減少。如果P(0)=∞，則即離下一次地震的時間隨著離逝時間的增加而增加。

2 各種分布的概率密度函數

假設上次地震起至現在的時間為t，其概率密度函數為p(t)，現在起至下次發生地震的間隔時間為t'的概率密度函數為P(t');現在起至下次發生地震間隔時間在u以內的概率為Pr(u)。則由(2)式可得

根據這些分布函數的定義，結合(2)式和(11)式用分布函數來計算下一次強震的等待時間概率。

2.1 指數分布

我們首先考慮指數分布，因為它與泊松分布相似，指數分布的等待時間的表達式為

其中t0是平均間隔時間。由(2)式，可得

很顯然，下一次地震的發生時間不取決于離逝時間，不管t的值有多大，從現在到下一次地震的平均時間都為t0。則

2.2 均勻分布

均勻分布的表達式是

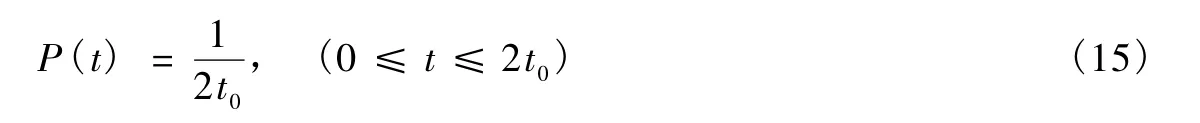
其中2t0是地震間最大的時間間隔，t0是其平均值。由(2)式，有

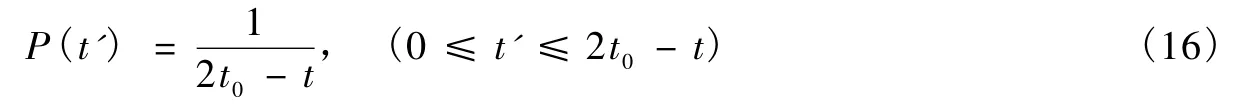
P(t')與t'無關，也就是說，它本身是一個均勻分布，但其值取決于t，在未來一直到t0的時間內，發生一次地震的概率隨著離逝時間的增加而增加，而當離逝時間超過2t0時，等待時間就變得不確定了。這實際上也就告訴我們，下一次地震的發生時間在2t0內的可能性最大，而這從公式也可以看出。如果是負的，這表明等待時間隨著離逝時間的減少而減少。則

2.3 威布爾分布

威布爾分布的表達式為

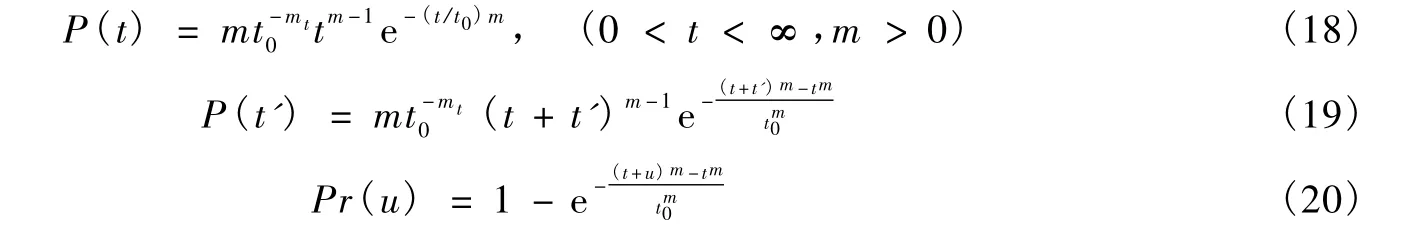
3 t0的確定

在上述計算中，我們不知道t0，所以要據有限的地震時間間隔來估計。假定我們有(n-1)個地震時間間隔，并忽略其不確定性(而這對歷史地震來說是可能的)。假定最后一次地震的離逝時間為t，那么，在泊松分布的情況下，由最大似然法給出的t0的估值是

t為最后一次地震距今的時間間隔，tj為n個地震間的時間間隔。

這樣，在泊松分布的情況下，得到了隨離逝時間的增加而增加的下一次地震復發的平均時間間隔。(21)式可以被推廣用于上述其他分布(Sornette et al，1997)。

4 強震的等待時間預測方法在河北及周邊地區的應用及回溯性檢驗

根據黃瑋瓊(1994)對我國大陸地震資料的完整性研究成果，按華北地區(除海域與邊遠地區外)的記載能力，對公元1303～1500年有記載的6級以上的地震和公元1500年后有記載的5級以上的地震，用統計分析方法進行檢驗，得出華北地區(除黃海及邊遠地區外)M地震自1484年之后基本完整。因此，本文將公元1500年以來的地震目錄(去除余震)用于等待時間的數學模型計算。

本文將預測研究區劃分成:河北南部、晉冀蒙、京津、唐山4個區域(表1)，用公元1500～1970年的5級以上的地震目錄計算了這4個地區從1970～2070年這100年內各時段發生5級及以上地震的概率(圖1)。

表1 研究區域的劃分

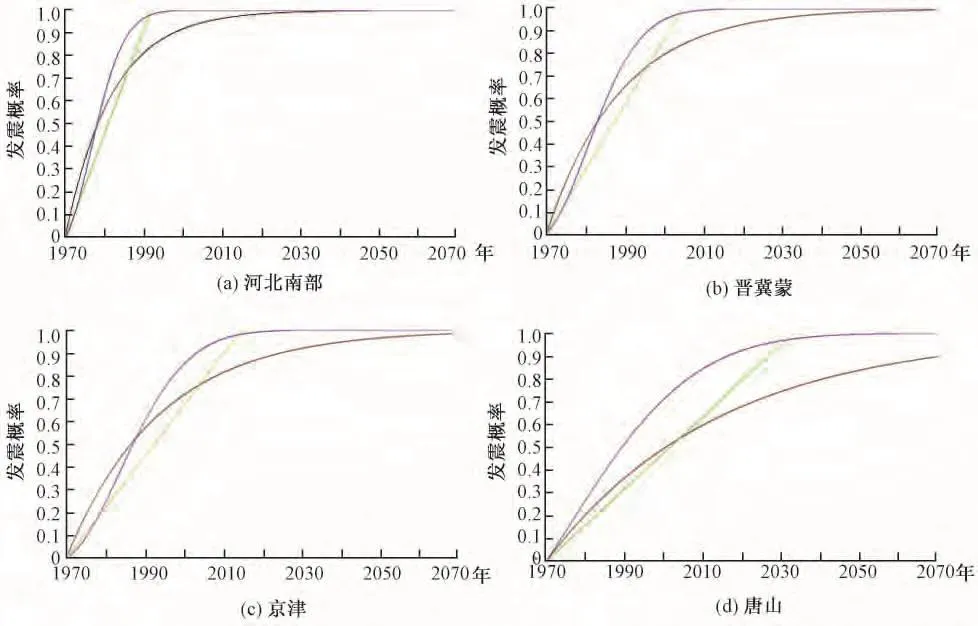
圖1 研究區域5級以上地震在1970～2070年的發震概率

本文設發震概率為P，當P≥0.6時，認為將會發生5級及以上的地震，則P=0.6是發生地震的最低閥值，因此對P=0.6、0.7、0.8這3個分布計算的發生5級及以上地震的概率值所對應的時間，進行回溯性檢驗。結果如表2～5所示。

據表2～5可以看出，河北南部和晉冀蒙地區檢驗率比較高，計算出來的發震時間和實際發震時間比較接近甚至一致。京津地區和唐山地區檢驗率略低一些，分析京津和唐山地區的計算過程發現，這兩個地區在1500～1970年間5級及以上地震的時間間隔比較大，這可能是造成檢驗率低的關鍵因素。

表2 河北南部地區回溯性檢驗結果的對比

表3 晉冀蒙地區回溯性檢驗的對比結果

表4 京津地區回溯性檢驗結果的對比

表5 唐山地區回溯性檢驗結果的對比

5 AIC判別準則

統計模型的優劣可以用(Akaike，1997)提出的一種AIC準則來判別，此準則實質上是一種最大熵估計。其方法是:假定lnL是所得到的模型的對數最大似然值，則

其中，L為統計分析中的最大似然數，K為參量數目。對于不同模型計算出的AIC值，AIC值最小的模型作為最優來選擇。兩個模型的AIC值相差越大，模型的優劣差別就越明顯，反之差別不大(朱守彪等，2002)。一般來說，AIC值相差2以上時，這兩個模型就可以比較其優劣(孫若昧等，1999)。

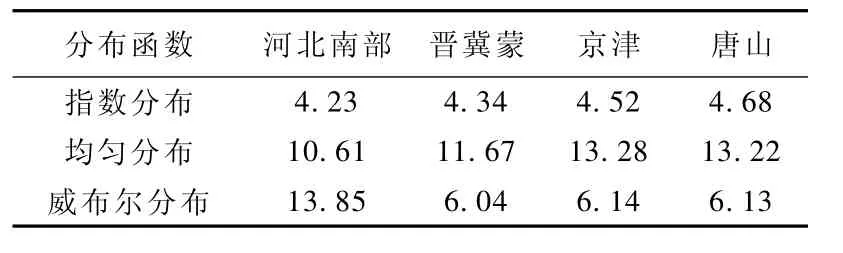
表6 研究區三個分布函數模型的AIC值

本文用AIC準則對研究區的3個分布函數模型進行判別，計算結果如表6。比較表6的AIC值，發現在這4個研究區內，3個分布函數模型中均是指數分布模型的AIC值最小，且這3個分布函數模型的AIC值都相差2以上，AIC準則適用于判斷這3個分布函數模型的優劣。結合回溯性檢驗的結果，本文認為指數分布模型比較適合于這4個研究區域內強震等待時間的計算。從圖1的(a)、(b)、(c)、(d)均可以看出在2013年以后的發震概率比較高，這為地震的中長期預測提供了參考。

6 討論和結論

研究發現，如果將本文的方法外推用于漸近估計非常大時間間隔的分布是危險的，而受計算中各個分布函數的特性和參數值的影響，該方法適用于通過短時間間隔的數據統計推斷出長時間尺度的強震等待時間的發震概率。

通過實例分析可以發現，重復時間的統計估計對所假定的分布是非常靈敏的，不同分布的等待時間發震概率有明顯差別，這可能與各地區歷史地震時間分布有關。且本文在用AIC準則判別統計模型的優劣時發現，研究所用的3個分布函數中，指數分布模型比較適合用于計算強震等待時間。

從計算結果和實例檢驗結果來看，強震等待時間的計算方法，對于中長期地震活動具有一定的預測能力，在今后的中長期地震預測中有待于進一步研究。