《平行四邊形的性質（1）》教學設計

宋曉瓊

【教材分析】

1.教材的地位和作用

“平行四邊形的性質”是北師大版八年級下冊第六章第一節的內容。它是在學生掌握了平行線、三角形及簡單圖形的平移等幾何知識的基礎上學習的。學習它不僅是對已學平行線、三角形等知識的綜合應用和深化，又是下一步學習矩形、菱形、正方形及梯形等知識的基礎，起著承上啟下的作用。

2.教學目標分析

（1）經歷探索平行四邊形有關概念和性質的過程，在活動中發展學生的探究意識和合作交流的習慣。

（2）探索并掌握平行四邊形的性質，并能簡單應用。

（3）在探索活動過程中發展學生的探究意識。

3.教學重難點

教學重點：對平行四邊形性質的探索。

教學難點：對平行四邊形性質的理解。

【學情分析】

關于平行四邊形的概念，在小學已經學過，八年級的學生對此并不會感到生疏，但對于這個概念的理解并不是十分深刻，所以，本節學習，并不是簡單的重復。“兩組對邊分別平行”是平行四邊形獨有的，用以區別于一般四邊形的本質屬性，這也是平行四邊形定義的核心所在。

關于平行四邊形邊、角的性質，經歷的是“感知、猜想、驗證、概括、證明”的認知過程；兩條性質的研究，先從邊分析，再從角分析，再到下一節課的從對角線分析，提供的是研究幾何圖形性質的一般思路。

【教法、學法分析】

教法：引導發現，探究合作。

教學流程：實踐探索，直觀感知—探索歸納，合作交流—推理論證，感悟升華—應用鞏固，深化提高—評價反思，概括總結。

學法：歸納總結，自主學習，合作交流。

【教學資源及環境（準備）】

1.教學用具

多媒體設備、三角板、平行四邊形的旋轉模型。

2.課前準備

學生、教師：兩個全等的平行四邊形，全等的三角形（多種類型）。

【教學過程】

第一環節：實踐探索，直觀感知

（10分鐘，動手實踐、探索、感知，學生進一步探索了平行四邊形的概念，明確平行四邊形的本質特征）

小組活動一：

內容：

準備兩個全等的三角形，將它們相等的一組邊重合，得到一個圖形。

觀察、討論：

（1）你拼出了怎樣的圖形？與同伴交流一下。

學生在投影儀上展示拼出的圖形。

學生可能會有不完整的地方，特別是一般的四邊形不容易出來，三角形也是一個容易忽視的問題，這需要教師來補充。

（設計意圖：雖然這一節講的是四邊形，但是為了不限制學生的思維，所以特意設計為將兩個全等的三角形相等的一組邊重合拼成一個圖形而不是設定為四邊形）

（2）你拼出的圖形中有平行四邊形嗎？如果有，你是怎么確定的，并與同伴交流。

（學生已經在七年級下和八年級上已經學習了相關的命題證明敘述，再加上剛才經歷了拼圖、觀察、討論的過程，教師可以就學生拼好的圖形問學生，從而讓學生思考：為什么是平行四邊形，什么是平行四邊形，從而總結出平行四邊形的定義）

（3）欣賞生活中的平行四邊形。

第二環節：探索歸納，合作交流

（10分鐘，學生動手、動嘴，全班交流）

平行四邊形的定義：兩組對邊分別平行的四邊形叫做平行四邊形。

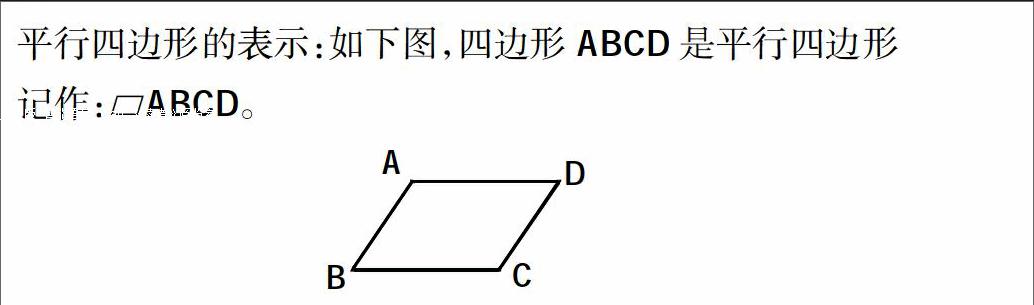
平行四邊形的表示：如下圖，四邊形ABCD是平行四邊形

記作：？荀ABCD。

■

平行四邊形不相鄰的兩個頂點連成的線段叫它的對角線。

平行四邊形相對的邊稱為對邊，相對的角稱為對角，相鄰的角稱為鄰角。

（設計意圖：讓學生在觀察的過程中，體會平行四邊形的定義的由來，從而總結并加深對平行四邊形定義的理解，為學好平行四邊形的判定作鋪墊）

小組活動二：

平行四邊形是中心對稱圖形嗎？如果是，你能找出它的對稱中心并驗證你的結論嗎？

你還發現平行四邊形有哪些性質？

（1）讓學生自己動手將手中的兩個全等的平行四邊形（用顏色區分開）旋轉180°后，看能否重合，觀察、分析。

（2）學生交流、議論。

（3）讓學生在投影儀上操作演示過程。

歸納：平行四邊形是中心對稱圖形，兩條對角線的交點是它的對稱中心。

平行四邊形的對邊相等，平行四邊形的對角相等。（多媒體展示）

平行四邊形的鄰角互補。（通過學生證明命題的過程引出）

你能證明它嗎？（學生自主對命題進行證明）

（將學生的證明情況在多媒體——投影儀上展示，并由學生說明每一步的理由，典型的例子重點講解）

（學生在投影儀上實際操作的過程中，可能會出現旋轉360°圖形還原或者是出現以任意一個頂點為對稱中心旋轉然后通過平移重合的情況，若有學生發現，要繼續追問學生為什么這樣是錯的，要怎么樣才對，而且最好對照中心對稱圖形的定義由學生來回答解決。在命題證明的過程中，學生可能出現敘述不當的地方，應及時評價、糾正）

（設計意圖：通過對結論的驗證，使學生能夠更好地掌握平行四邊形的有關性質，規范證明的格式，學生容易接受，易于理解記憶，在解題時也節省時間）

第三環節：推理論證，感悟升華

（10分鐘，學生通過說理，由直觀感受上升到理性分析，在操作層面感知的基礎上提升，并了解圖形具有的數學本質）

已知：如下圖，在平行四邊形ABCD中，E，F是對角線AC上的兩點，并且AE=CF。

求證：BE=DF。

證明：∵四邊形ABCD是平行四邊形（已知）

∴AB=CD（平行四邊形的對邊相等）

AB//CD（平行四邊形的定義）

∴∠1=∠2（兩直線平行，內錯角相等）

又∵AE=CF（已知）

∴△ABE≌△CDF（SAS）

∴BE=DF（全等三角形的對應邊相等）

（此部分內容由學生負責完成講解，不足之處由學生或教師指出訂正）

（設計意圖：通過學生自己講解例題，體會證明的過程，進一步掌握證明題的方法和步驟）

第四環節：應用鞏固，深化提高

（10分鐘，通過議一議、練一練，學生進一步理解平行四邊形的性質，并進行簡單合情推理，體現性質的應用）

實踐、探索內容。

（1）在？荀ABCD中，∠B=60°，BC=3 cm，則∠A=120°，∠D=60°，AD=3 cm.

（2）在？荀ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（D）

A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.1∶2∶1∶2

（3）游戲：利用平行四邊形設計美麗的圖案。

讓學生展利用平行四邊形設計的美麗圖案，表達自己美好的愿望。

（設計意圖：通過學生自己設計圖案的過程，讓學生充分體會平行四邊形在生活中的美，表達出對生活的美好愿望）

第五環節：評價反思，概括總結

（5分鐘，學生踴躍談感受和收獲）

活動內容：

師生相互交流、反思、總結：本節課學到了什么？（知識上、方法上）

（設計意圖：通過對知識的總結，使學生對平行四邊形的概念與性質掌握的更加條理、清晰）

【作業布置】

必做題：習題6.1的第1題、第2題、第3題。

選做題：利用平行四邊形的性質設計一道題目，要求用上平行四邊形的四條性質。

編輯 韓 曉