核電站控制棒驅動機構隔磁片應力分析

曲大莊，李 晨，錢 浩，朱 寶，詹陽烈，景 益，劉 剛

（1.國家核電技術公司，北京100029；2.上海核工程研究設計院，上海200233；3.大連理工大學材料科學與工程學院，遼寧大連116024）

壓水堆核電站通過改變或保持控制棒驅動機構組件在垂直方向上的位置來實現反應堆的啟停、正常工況下堆芯功率的調節或保持以及事故工況下的快速釋棒停堆.控制棒驅動機構的主要部件為：承壓殼體部件、鉤爪部件、磁軛線圈部件、驅動桿部件、導磁半環和導向隔熱套等.位于殼外的磁軛線圈通電后將產生電磁場并帶動裝在殼內的部件（鉤爪部件、驅動桿部件）步躍運動，使銜鐵直線向上運動直至撞擊到由磁極支撐的隔磁片上.當磁軛線圈斷電電磁場消退時，銜鐵在自重和彈簧力的作用下脫離隔磁片豎直向下運動，設置在磁極和銜鐵之間的隔磁片起到了加快機構釋放速度的功效.

為滿足反應堆啟停及功率調節的需要，控制棒驅動機構在設計壽期內要經歷數百萬次的步躍運動，對于大部分設計壽命在40年左右的第二代核電技術，步躍約為200萬步；而設計壽命在60年的第三代核電技術則要求600萬步.在過去的運行經驗中，控制棒驅動機構的主要失效形式是鉤爪部件銷軸和銷軸孔的磨損所引起的失步和滑步，但隨著控制棒驅動機構設計壽命的大幅度提高，除了原有的失步、滑步失效形式外，又發現了隔磁片在一定次數步躍運動后的疲勞破損現象，已經引起業界的高度關注.

在控制棒驅動機構的實際工作過程中，對于驅動機構的每一次步躍運動，磁軛線圈的電磁場都會使銜鐵撞擊隔磁片，使隔磁片不斷受到沖擊載荷.在結構上，隔磁片為具有內、外徑的軸對稱薄壁圓盤，其法平面的一側始終與磁極接觸（或分離），另一側的內徑區域始終與壓緊彈簧緊密接觸，外徑區域則受到銜鐵撞擊的沖擊載荷.顯然，準確分析隔磁片在銜鐵沖擊載荷作用下的應力分布及具體數值，對于控制棒驅動機構的安全設計及壽命預估顯得尤為重要.如文獻［1］中將應力分析的結果應用到疲勞安全性分析中.

筆者根據彈性力學［2］板殼理論建立了隔磁片在銜鐵沖擊載荷作用下的基于磁極彈性基礎的薄壁圓盤軸對稱彎曲應力分析模型，直接利用冪級數給出了微分方程的解析式.由于作用在隔磁片上的載荷沿徑向并非連續，與磁極的接觸在一般情況下也不一定連續，因此需要將隔磁片沿徑向分解成幾個圓盤，根據分界處內力平衡和位移連續條件，利用傳遞矩陣技術建立了整體平衡方程，并根據隔磁片內、外徑的自由邊界條件得到了問題的全部解.

利用所提出的方法對某在建核電站控制棒驅動機構的隔磁片在銜鐵撞擊達到最大沖擊載荷時的工況進行了應力分析計算，得到了相關的應力分布和具體數值，與有限元數值計算結果進行了比較，并通過已經出現的隔磁片沖擊疲勞破損事例的驗證，為核電站控制棒驅動機構的結構設計以及隔磁片的沖擊疲勞和失效機理等分析提供了理論依據.

1 薄壁圓盤軸對稱彎曲的微分方程及解析解

若將隔磁片簡化成如圖1所示的置于磁極彈性基礎的薄壁圓盤，當法向載荷為q，基礎彈性系數為ks時，令w為圓盤的法向位移，為圓盤的平均半徑，并且r＝x，＝q，＝ks，則有圓盤軸對稱彎曲的微分方程為

式中：D為圓盤彎曲剛度，且；μ為泊松比；h為圓盤厚度；E為圓盤材料彈性模量.

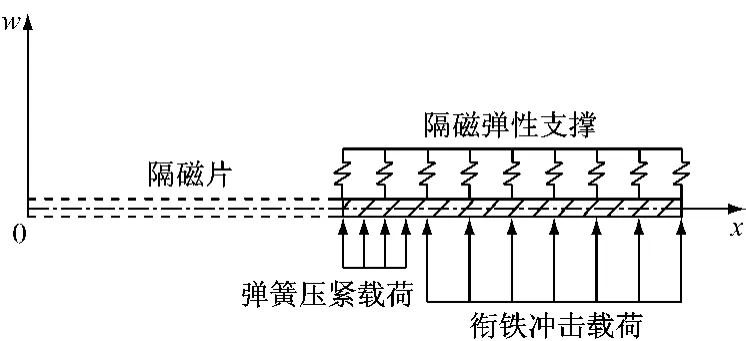
圖1 隔磁片軸對稱薄壁圓盤Fig.1 Axisymmetrical thin disk of the magnetic isolation shim

式（1）的求解與隔磁片和磁極是否接觸有關.當二者分離時，即ks＝0時式（1）的全部解可直接由彈性理論分析結果得到，即（，為常數）

式中：C1～C4為待定系數.

當隔磁片與磁極有接觸，即ks≠0 時，雖然式（1）已有基于Bessel特殊函數的經典解［3-4］，但為了數學上的方便，還可以直接采用冪級數解，即

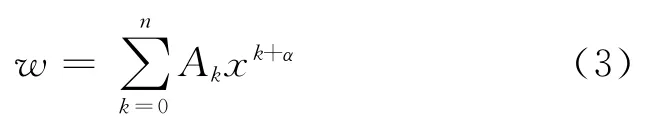
根據式（1）的齊次方程以及待定系數α應滿足的條件，可得到對應于A0≠0，A1＝A2＝A3＝0 時的α1＝0，α2＝2.將α1和α2分別代入式（3），可得式（1）的2個線性無關解

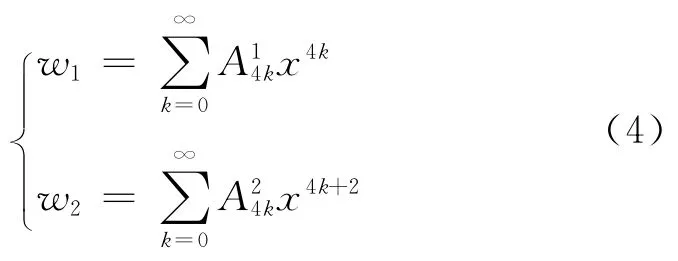
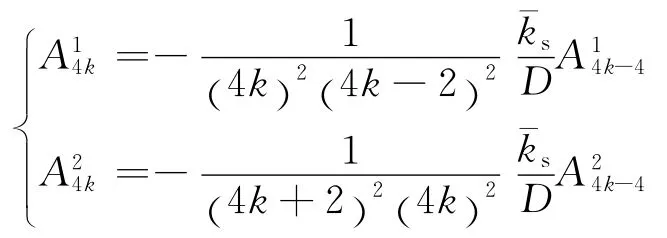
由于式（1）是一個4階方程，需要有4個線性無關解來構成其通解，因此可仿照求解Bessel方程［5］的方法給出另外2個線性無關解，即

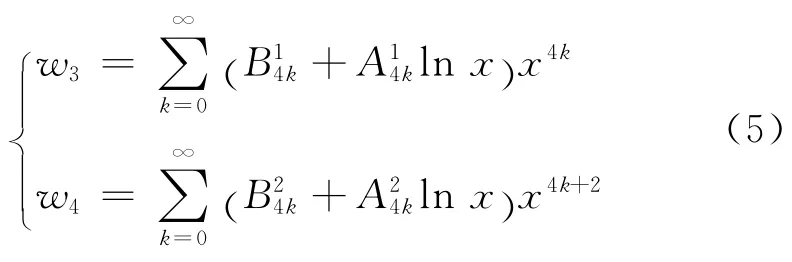
式中：

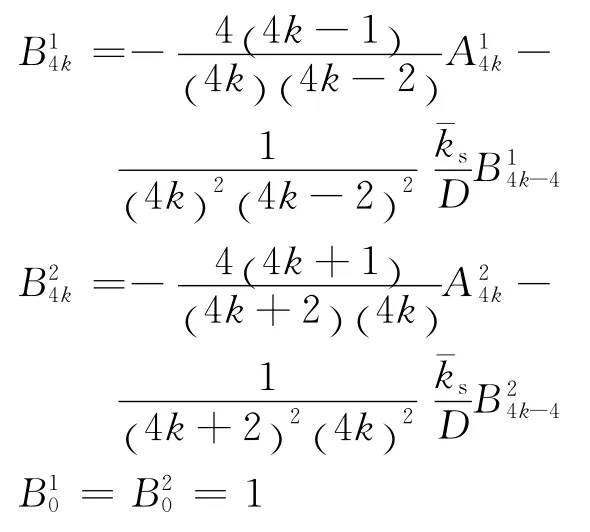
式（1）的特解取決于載荷的分布形式，當其為常數時，有.與式（3）線性組合得到式（1）的全部解

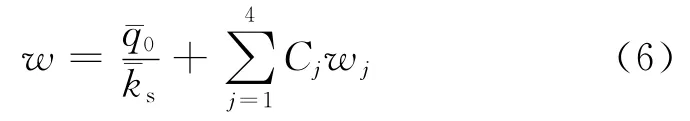
顯然，式（2）或者式（6）分別給出的便是隔磁片在法向載荷q作用下與磁極分離或者接觸時薄壁圓盤軸對稱彎曲的微分方程的解析解.

2 隔磁片狀態向量的傳遞及整體平衡方程

根據隔磁片上彈簧壓緊載荷和銜鐵沖擊載荷沿徑向的分布情況以及與磁極彈性支撐的接觸情況，可將隔磁片沿徑向分解成幾個薄壁圓盤.對于其中的任何一個均可定義其邊界上的物理量，，，并根據圓盤軸對稱彎曲時位移w與轉角φ、彎矩M和剪切力F的關系（式（7））

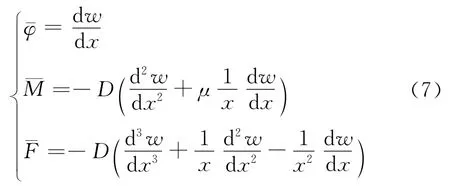
結合式（2）或者式（6）建立隔磁片分段后各段的狀態向量方程

式中：

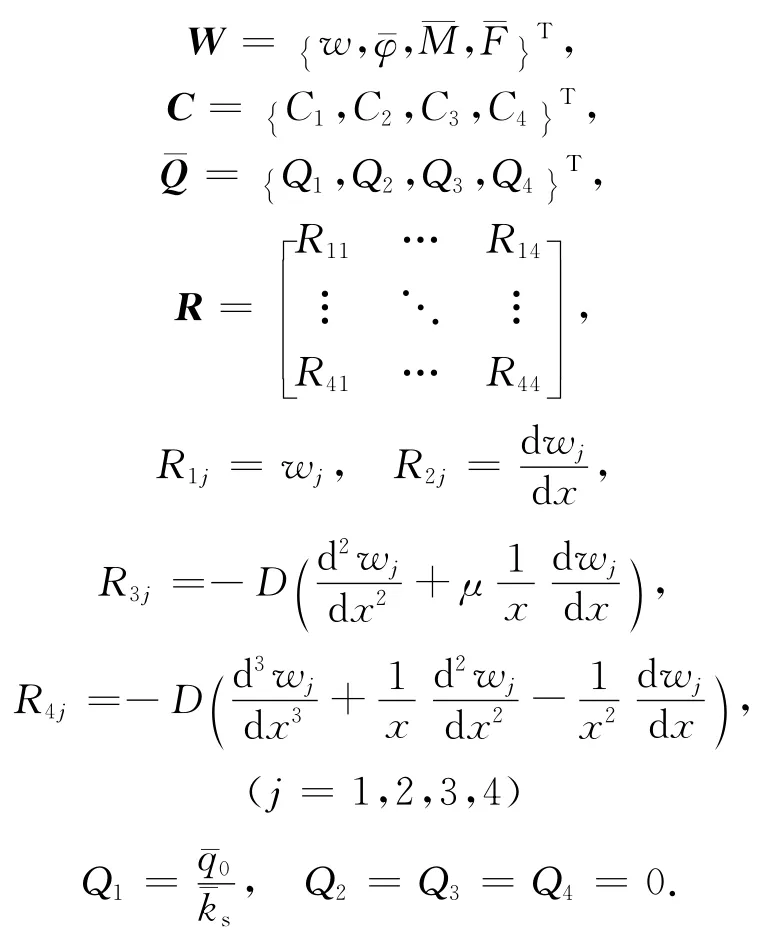
當把隔磁片分解為m段時，可根據第k段內、外徑r0和rn處的狀態向量和，定義傳遞矩陣，得到同一段圓盤內、外徑兩端的狀態向量關系

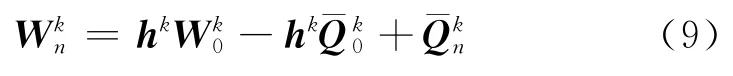
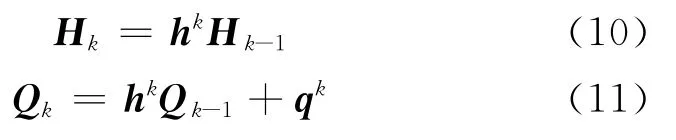
遍取k＝1，2，…，m，最終得到隔磁片整體內、外徑兩端的狀態向量關系，即隔磁片應力分析的整體平衡方程

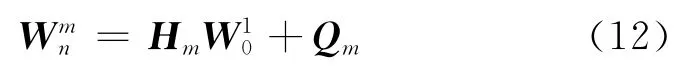
由于隔磁片內、外徑兩端的邊界條件為自由狀態，即當r＝r0時，M0＝F0＝0，以及當r＝rm時，Mm＝Fm＝0，因此將它們帶入上式可以得到

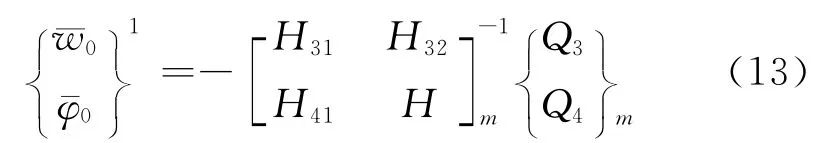
利用式（9）的傳遞關系，可最終確定各分段界面處的狀態向量，以及各段內不同徑向位置r＝ri的狀態向量.

除前述隔磁片狀態向量中M所代表的徑向彎矩Mr外，在圓盤軸對稱彎曲問題中還有切向彎矩Mθ.根據

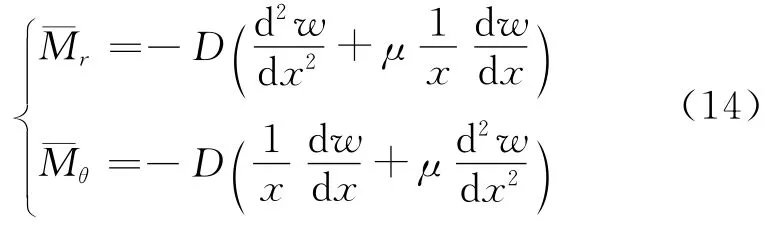
并考慮到＝dw／dx，有關系式

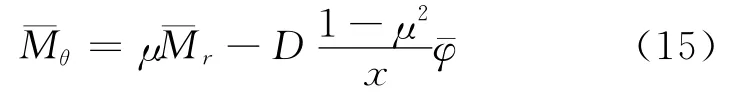
進而得到隔磁片上下表面處的徑向彎曲應力σr和切向彎曲應力σθ

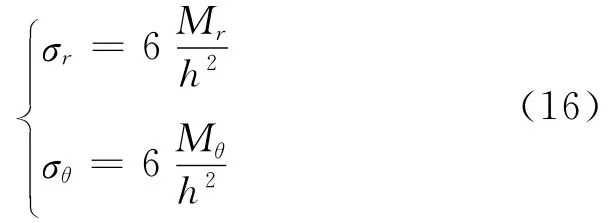
其中，σr和σθ都是徑向位置的函數.

3 隔磁片應力計算結果以及與有限元數值計算結果的比較

利用筆者提出的方法對某在建核電站控制棒驅動機構的隔磁片在銜鐵撞擊達到最大沖擊載荷時的工況進行應力分析計算，相關數據為：隔磁片內徑r0＝30.70mm，壓緊彈簧處外徑r1＝37.00mm，銜鐵處內徑r2＝39.40 mm，隔磁片外徑r3＝63.25 mm，圓盤厚度h＝1.59 mm，材料彈性模量E＝1.90×1011N／m2，材料泊松比μ＝0.3，磁極支撐彈性系數ks＝1.35×1012N／m3，彈簧壓緊載荷Pz1＝480N，銜鐵最大沖擊載荷Pz2＝6.11×105N.為了比較，采用Ansys有限元分析軟件中軸對稱殼單元和彈簧單元對同樣的隔磁片分析模型進行了最大沖擊載荷下的應力計算.有限元分析隔磁片采用Shell208 軸對稱殼單元模擬，彈性支撐采用Combin14線性彈簧模擬.有限元分析模型和邊界條件如圖2 所示，對Combin14彈簧單元彈性支撐端節點約束隔磁片法向位移自由度.載荷條件如圖3所示.所有輸入參數與第2節理論公式計算參數一致.

圖2 有限元分析模型和邊界條件Fig.2 FEA model and boundary conditions

2種分析方法的計算結果同時示于圖4～圖7，從圖中可以清晰地看到二者完全吻合.

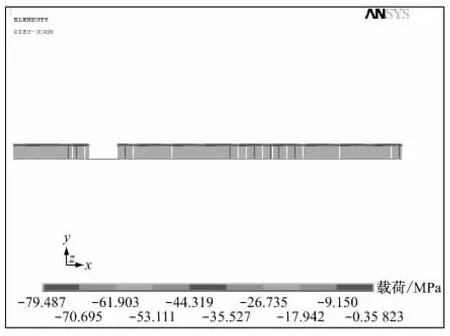
圖3 載荷條件Fig.3 Loading conditions

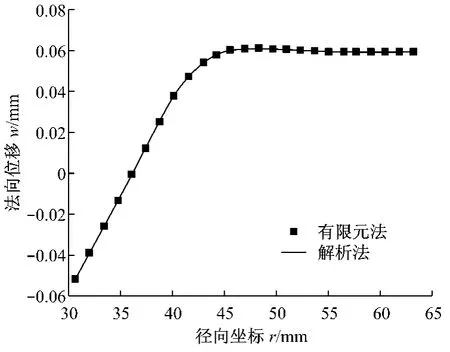
圖4 法向位移Fig.4 Normal displacement

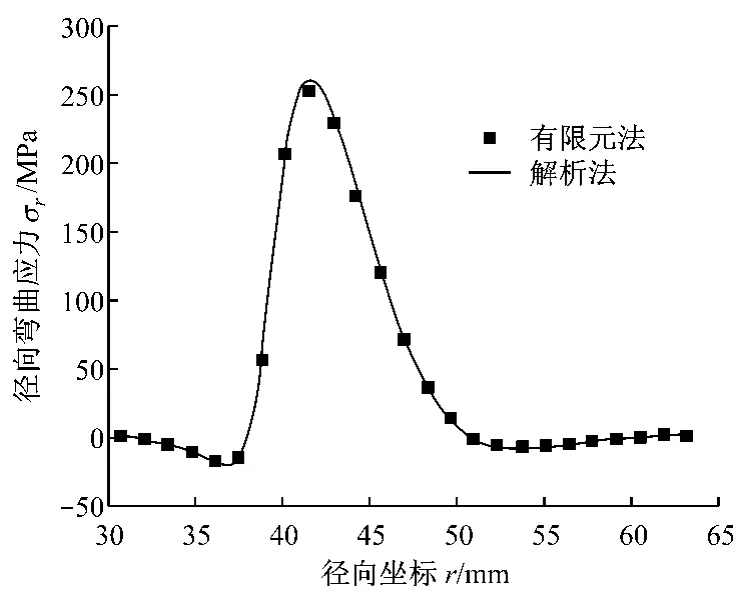
圖5 徑向彎曲應力Fig.5 Radial bending stress

如圖4所示，銜鐵撞擊到隔磁片沖擊載荷達到最大值后，隔磁片在內徑r＝36.2 mm 附近與磁極發生分離，或者說雖然有壓緊彈簧，但在最大沖擊載荷時它不能保持隔磁片始終與磁極相接觸.

與隔磁片沖擊疲勞相關的拉應力發生在隔磁片與磁極接觸側，圖5和圖6分別給出了該側隔磁片的徑向和切向彎曲應力，在半徑r＝42.0 mm 附近二者均出現最大值σr＝259 MPa、σθ＝58 MPa.圖7給出了隔磁片與磁極之間的軸向壓應力，最大值約為σz＝82 MPa.

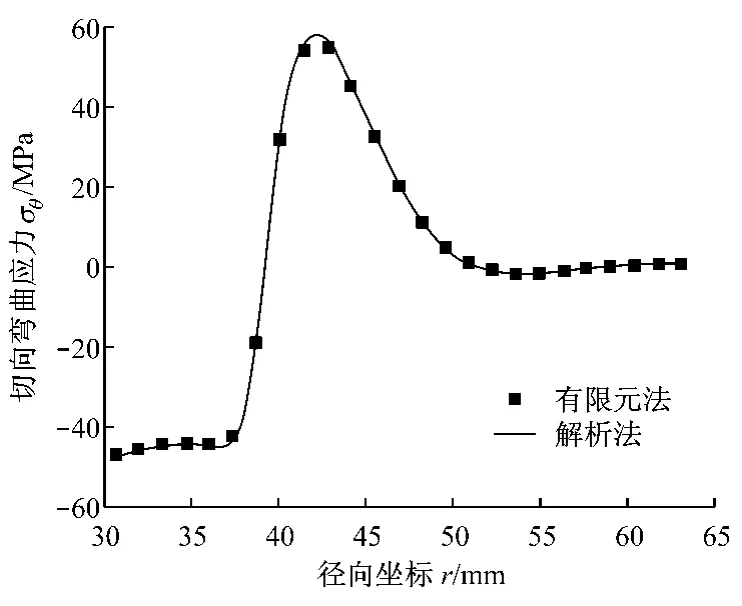
圖6 切向彎曲應力Fig.6 Tangential bending stress

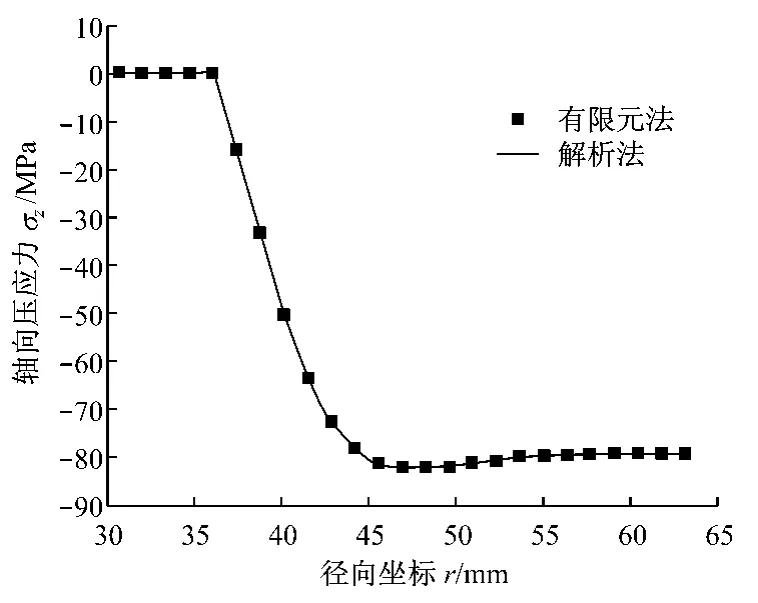
圖7 軸向壓應力Fig.7 Axial compressive stress

對于隔磁片的沖擊疲勞，可根據材料疲勞最大變形能理論［6］確定疲勞等效應力

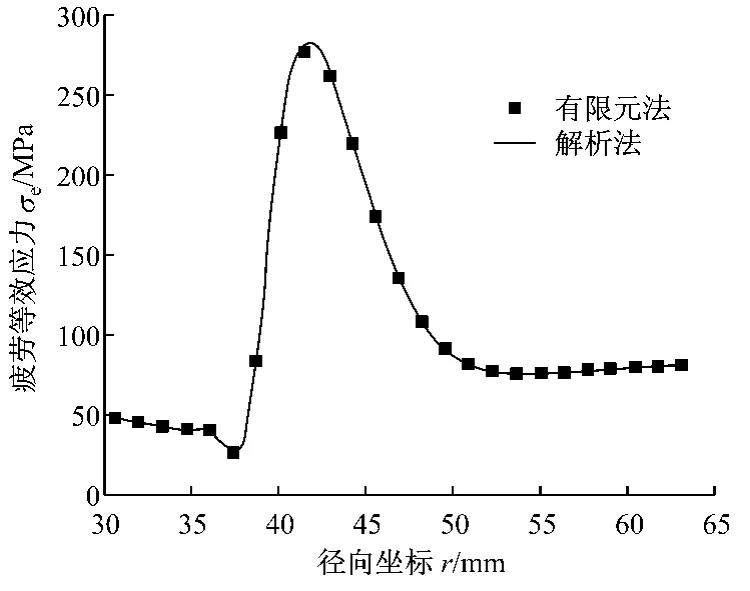
圖8 疲勞等效應力Fig.8 Equivalent fatigue stress

圖8給出了將各應力分量結果代入上式所得到的疲勞等效應力.從圖8可以看出，最大疲勞等效應力σe＝283 MPa，發生在距離內徑約1／3隔磁片徑向寬度處，它以徑向拉應力σr為主體，是導致隔磁片經歷一定次數步躍運動的銜鐵沖擊載荷作用后出現疲勞破損的主要原因，與隔磁片沖擊疲勞破損事例裂紋的起始位置和擴展模式相符.

4 結 論

（1）雖然有壓緊彈簧，但隔磁片不能始終與磁極保持接觸，在銜鐵最大沖擊載荷作用下，隔磁片將產生彎曲變形并在壓緊彈簧附近與磁極發生分離，導致與磁極接觸側出現與沖擊疲勞相關的彎曲拉應力.

（2）隔磁片與磁極接觸側處于三維應力狀態，可根據材料疲勞的相關理論確定相應的疲勞等效應力.以徑向拉應力為主體的最大疲勞等效應力發生在距離內徑1／3隔磁片徑向寬度處，它是導致隔磁片經歷一定次數步躍運動的銜鐵沖擊載荷作用后出現疲勞破損的主要原因.

（3）所提方法的分析結果與隔磁片沖擊疲勞破損事例裂紋的起始位置和擴展模式相符合，可以為核電站控制棒驅動機構的結構設計以及隔磁片的沖擊疲勞和失效機理等分析提供理論依據.

［1］史進淵，鄧志成，汪勇，等.汽輪機轉子初始裂紋高周疲勞安全性分析方法及其在焊接轉子中的應用［J］.動力工程學報，2013，33（1）：17-24.

SHI Jinyuan，DENG Zhicheng，WANG Yong，etal.High cycle fatigue safety analysis for steam turbine rotors with initial crack and its application to a welded rotor［J］.Journal of Chinese Society of Power Engineering，2013，33（1）：17-24.

［2］徐芝綸.彈性力學［M］.北京：高等教育出版社，2006.

［3］黃義，何芳社.彈性地基上的梁、板、殼［M］.北京：科學出版社，2005.

［4］楊奇林.數學物理方程與特殊函數［M］.北京：清華大學出版社，2011.

［5］鐵摩辛柯S，沃諾斯基S.板殼理論［M］.北京：科學出版社，1977.

［6］鐵摩辛柯S.材料力學［M］.北京：科學出版社，1979.