鐵路客車軸箱軸承接觸潤滑機理

胡欣，常偉，奚卉，張茜，王鳳才

(1.武漢科技大學(xué) 鐵路技術(shù)及摩擦學(xué)研究中心,武漢 430081；2.西安交通大學(xué) 軸承技術(shù)研究中心,西安 710049；3.聯(lián)合制造及軸承產(chǎn)業(yè)技術(shù)研究中心,銀川 750000；4.瓦房店軸承集團股份有限責(zé)任公司, 遼寧 瓦房店 116300)

軸箱軸承是鐵路車輛最重要的組成部分，其產(chǎn)品質(zhì)量與技術(shù)性能直接關(guān)系到鐵路車輛運行的安全性、可靠性以及維護費用，是鐵路車輛監(jiān)控或維護的重點，幾乎所有鐵路車輛上都安裝有與之相關(guān)的軸箱溫升等信號報警系統(tǒng)。雖然鐵路運行部門和軸承制造業(yè)對于軸箱軸承產(chǎn)品質(zhì)量和安裝使用過程有著嚴格規(guī)定與控制，但由于受給定運行工況條件下箱體變形與軸承組件制造及安裝誤差等因素的影響，鐵路客車軸箱軸承的安全運行常面臨著諸如滾道疲勞剝落、潤滑失效及熱軸等問題的威脅。因此，開展鐵路客車軸箱系統(tǒng)多界面接觸潤滑性能機理研究顯得愈來愈重要，這同時有助于推動軸箱軸承產(chǎn)品關(guān)鍵技術(shù)的發(fā)展[1-6]。

近年來，隨著鐵路客車提速發(fā)展的要求，鐵路部門與軸承行業(yè)均提出了研究與開發(fā)時速為160 km及以上的鐵路客車軸箱軸承的發(fā)展計劃。然而，原有120 km/h運行工況下，發(fā)生概率較高的軸承滾道疲勞問題及產(chǎn)品關(guān)鍵技術(shù)一直沒有得到根本解決，這妨礙了鐵路客車提速及軸箱軸承技術(shù)的發(fā)展。因此，為滿足鐵路客車提速要求以及為更高運行速度條件下的鐵路客車軸箱軸承技術(shù)的發(fā)展提供平臺，需要有效地識別數(shù)值模擬軸箱軸承的接觸載荷、應(yīng)力及位移分布情況，這涉及鐵路軸箱系統(tǒng)大規(guī)模彈性接觸耦合系統(tǒng)求解問題，而軸箱軸承接觸潤滑機理研究目前仍處于起步階段。需要指出的是，針對120～160 km/h的鐵路客車軸箱軸承的研究，能夠從產(chǎn)品基礎(chǔ)技術(shù)機理和產(chǎn)業(yè)化技術(shù)發(fā)展積累的經(jīng)驗基礎(chǔ)上，推動更高速度工況條件下鐵路客車軸箱軸承(包括高鐵軸承)的研究與發(fā)展。在產(chǎn)業(yè)化技術(shù)發(fā)展上，如果缺乏對鐵路軸箱軸承基礎(chǔ)性技術(shù)機理認識的積累，僅僅追求對高速工況下的高速鐵路軸承進行研究是缺乏技術(shù)發(fā)展基礎(chǔ)的，在戰(zhàn)略上可能會影響中國鐵路軸承的技術(shù)進步與發(fā)展機遇。

鐵路軸箱軸承的摩擦學(xué)性能關(guān)乎著鐵路提速客車軸承運行的可靠性與安全性。典型軸箱系統(tǒng)及2套圓柱滾子軸承組件間，在運行工況條件下表現(xiàn)出耦合彈性系統(tǒng)多界面接觸行為。因此，發(fā)展多界面接觸行為機理研究模型，可以為軸箱軸承潤滑模型的建立與發(fā)展提供較為真實的接觸載荷分布條件，并且為軸承滾子與滾道間潤滑接觸行為機理的認識提供支持[7-10]。值得一提的是，鐵路軸箱彈性系統(tǒng)多界面接觸模型的建立和發(fā)展，有效地推動了鐵路軸箱軸承接觸機理和產(chǎn)品技術(shù)識別的發(fā)展，對理解鐵路車輛軸承接觸、潤滑、摩擦、溫升以及磨損等多方面的問題有著重要意義。

下文以鐵路提速客車軸箱軸承(NJ3226與 NJP3226)為對象，通過建立的軸箱彈性系統(tǒng)多界面接觸模擬平臺獲得軸箱軸承滾子與內(nèi)、外圈間的接觸載荷分布情況；接著，給出鐵路軸箱軸承脂潤滑彈性流體潤滑模型和相應(yīng)的數(shù)值模擬方法；然后，基于軸箱多界面接觸機理模擬系統(tǒng)和脂潤滑模型，分析了不同速度和載荷工況條件下鐵路軸箱軸承的潤滑性能；最后，通過比較，研究了速度、載荷等因素對軸箱軸承潤滑的影響機理，為鐵路提速客車軸箱軸承微尺度設(shè)計制造及安裝服役提供技術(shù)支持。

1 模型與方法

鐵路客車每個軸箱裝用2套圓柱滾子軸承，輪軸與軸承內(nèi)圈為過盈配合，軸承外圈與箱體為間隙配合。2套軸承與軸和箱體的配合量有所不同，即存在配合相互差。鐵路客車軸箱軸承系統(tǒng)結(jié)構(gòu)模型如圖1所示，其中，軸箱系統(tǒng)由NJ3226和NJP3226軸承組成，軸承外徑D=250 mm，軸承內(nèi)徑d=130 mm，內(nèi)圈寬度B=80 mm，滾子直徑Dw=32 mm，滾子長度Lw=52 mm，滾子彈性模量E1=219 GPa，軸承套圈以及箱體的彈性模量E2=207 GPa，輪軸的彈性模量E3=210 GPa，軸箱系統(tǒng)組件的泊松比ν=0.3。

1—滾子；2—軸箱前蓋；3—壓板螺栓；4—壓板；5—軸箱體；6—軸承外圈(外側(cè))；7—平擋圈；8—保持架；9—內(nèi)圈(無固定擋邊)；10—軸承外圈(內(nèi)側(cè))；11—內(nèi)圈(有固定擋邊)；12—密封圈；13—防塵擋圈

1.1 軸承運動模型及工況條件

針對軸箱軸承系統(tǒng)模型建立多界面接觸力學(xué)模型，并以此求解軸承的多界面接觸力學(xué)問題，在徑向載荷Fr=89 kN的條件下，對滾子與滾道的徑向接觸載荷分布進行分析求解，如圖2所示。可以看出，鐵路軸箱及其軸承組件構(gòu)成了一個復(fù)雜的多界面彈性接觸系統(tǒng)，載荷引起的整體變形與界面接觸以及摩擦學(xué)行為，需通過接觸模型、潤滑模型以及相應(yīng)的數(shù)值模擬方法進行研究。

圖2 軸箱軸承載荷工況模型及載荷分布

鐵路客車軸箱軸承滾子相對滾道的運動模型及坐標系統(tǒng)如圖3所示。軸承內(nèi)圈角速度為ω，滾子自轉(zhuǎn)角速度為ωR，滾子公轉(zhuǎn)角速度為ωm；軸承內(nèi)、外滾道半徑和滾子半徑分別為R1=0.079 m，R2=0.111 m，R3=0.016 m。假設(shè)彈流潤滑時軸承內(nèi)部運動關(guān)系為純滾動，即滾子表面速度等于內(nèi)、外滾道表面速度，由此可得

圖3 滾子運動模型及坐標系統(tǒng)

R3ωR=R2ωm，

(1)

R3ωR=R1(ω-ωm)，

(2)

(3)

(4)

軸箱軸承滾子與內(nèi)、外圈接觸點的表面平均速度(卷吸速度)為

(5)

式中：N為輪軸的轉(zhuǎn)速，r/min。

滾子與滾道的當(dāng)量曲率半徑分別為

(6)

(7)

式中：Ri,Re分別為滾子與內(nèi)、外滾道接觸處的當(dāng)量曲率半徑。

1.2 軸箱接觸模型

針對軸箱彈性耦合系統(tǒng)，運用有限元法建立了軸箱軸承多界面接觸力學(xué)模型，該模型是鐵路客車軸箱多界面大規(guī)模模擬平臺的一個重要組成部分，考慮了給定工況下軸承各組件之間的復(fù)雜多界面接觸行為以及輪軸的變形等因素。有關(guān)鐵路客車軸箱彈性系統(tǒng)及軸承多界面接觸模型和方法，將另文給出，不再贅述。

1.3 潤滑模型

鐵路客車軸箱軸承脂潤滑控制方程包括潤滑壓力、油膜厚度、黏壓關(guān)系及相應(yīng)載荷平衡方程等，具體描述如下：

(1)潤滑方程。彈流潤滑狀態(tài)下滾子與滾道間可以視為純滾動,故可忽略滾子相對滾道接觸面y方向的運動以及U隨x的變化，滾子與滾道間的彈性接觸問題經(jīng)幾何模擬和彈性模擬，可以轉(zhuǎn)化成當(dāng)量曲率半徑為R和當(dāng)量彈性模量為E′的彈性圓柱與剛性平面的接觸，由此得到脂潤滑壓力方程，即Reynolds方程[10-11]為

(8)

式中：p為潤滑應(yīng)力；h為油膜厚度；n為流變參數(shù)，n≤1；η為潤滑脂的動力黏度；ρ為潤滑脂密度。經(jīng)量綱歸一化后選取求解域，可設(shè)求解區(qū)域的入口區(qū)xin=-1.5，出口區(qū)xout=1.5，即計算結(jié)果圖中橫坐標x。

(2)膜厚方程。滾子與滾道間的潤滑油膜厚度[10-11]為

，(9)

式中：s為x軸上的附加坐標，表示任意線載荷p(s)ds與坐標原點之間的距離；p(s)為載荷分布函數(shù)；x0和xe分別為載荷p(x)的起點和終點坐標；R為等效曲率半徑。

(3)黏壓方程。采用脂潤滑模型的黏壓方程[10-11]為

η=η0exp{lnη0+9.67[(1+5.1×10-9p)z-1]}，

(10)

式中：z為常數(shù)，近似取值0.68；η0為潤滑脂在常壓下的動力黏度。

(4)最小油膜膜厚。脂潤滑時滾子與外滾道最小油膜厚度計算公式可通過Hamrock-Dowson式計算[11]

he,min=0.336[R3(1+λ)]1.13α0.54(η0n)0.7·

(11)

滾子與內(nèi)滾道的最小油膜厚度公式[11]為

hi,min=0.336[R3(1-λ)]1.13α0.54(η0n)0.7·

(12)

式中：α為黏壓系數(shù)，m2/N；n為流變參數(shù)；E′為當(dāng)量彈性模量,GPa;W為滾子單位長度上的載荷，假定滾子總接觸載荷為Q，有效長度為L，則W=Q/L。設(shè)計的脂潤滑模型各參數(shù)的取值見表1。

表1 軸承潤滑性能分析參數(shù)

2 試驗分析

根據(jù)鐵路客車軸箱軸承服役條件，選取80，100，120，140和160 km/h 共5組運行速度，結(jié)合不同載荷工況，對鐵路列車潤滑狀況進行模擬。考慮載荷變化較大等情況，潤滑計算采用較高的網(wǎng)格密度，將系統(tǒng)的基本方程進行無量綱化后得到離散方程，然后通過迭代求解方程得到所需結(jié)果。程序的迭代過程包括潤滑應(yīng)力修正與載荷平衡所需的剛體位移修正。對于潤滑應(yīng)力修正，在低壓區(qū)選用Gauss直接迭代法求解，在應(yīng)力變化較大區(qū)域采用雅各比迭代法，以保證應(yīng)力迭代收斂的穩(wěn)定性。

2.1 接觸載荷

軸箱內(nèi)、外側(cè)軸承各滾子與滾道的徑向接觸載荷分布情況見表2[7]。

由表2可知，除去接觸載荷為0的滾子，在同等工況條件下，內(nèi)側(cè)軸承滾子與滾道間的徑向接觸載荷均大于外側(cè)軸承。滾子在不同位置承受的接觸載荷也不同，其中7#滾子承受的接觸載荷Q7最大，其余各滾子承受的載荷依次減小并基本呈對稱分布狀態(tài)。軸頸變形使得內(nèi)側(cè)和外側(cè)軸承徑向接觸載荷呈現(xiàn)非均勻分布狀態(tài)[6]。

表2 軸承各滾子與滾道的徑向接觸載荷 kN

2.2 潤滑性能

2.2.1 模型驗證

為驗證潤滑模型計算的合理性，以軸箱內(nèi)側(cè)軸承為例，在v=120 km/h時，將模型的計算結(jié)果與Hertz接觸應(yīng)力及油膜厚度公式計算結(jié)果進行對比，結(jié)果分別見表3和表4。

表3 滾子與內(nèi)/外滾道間的最大接觸應(yīng)力

表4 滾子與內(nèi)/外滾道間的最小油膜厚度

由表3可知，承載較大滾子的模型計算結(jié)果與Hertz接觸應(yīng)力十分接近，誤差均在5%左右；而輕載滾子的誤差稍大，在15%左右。由表4可知，在主承載區(qū)，模型計算結(jié)果與公式計算結(jié)果非常接近；在超輕載區(qū)，雖然兩者誤差較大，但在數(shù)量級上仍具有參考價值。結(jié)合潤滑應(yīng)力和最小膜厚的對比分析，證明潤滑模型合理，能夠用于軸箱軸承潤滑性能分析。

2.2.2 潤滑性能分析

以軸箱內(nèi)側(cè)軸承為例進行潤滑性能分析。不同時速下，7#滾子與內(nèi)圈滾道的潤滑應(yīng)力和油膜厚度分布如圖4所示。時速120 km/h時，內(nèi)側(cè)軸承各滾子的潤滑應(yīng)力與油膜厚度分布如圖5所示。

圖4 速度對軸箱內(nèi)側(cè)軸承潤滑性能的影響

圖5 內(nèi)側(cè)軸承滾子與內(nèi)滾道間的潤滑性能

由圖可知，軸箱軸承脂潤滑潤滑應(yīng)力及油膜厚度分布具有以下特征：

(1)在接觸區(qū)域中部，潤滑應(yīng)力呈現(xiàn)近似Hertz接觸應(yīng)力的分布特征(圖4a)，而相應(yīng)的油膜厚度曲線呈現(xiàn)近似平行的分布狀況。當(dāng)接觸載荷明顯減小時，潤滑應(yīng)力將逐漸偏離Hertz分布(圖5a)。

(2)在出口區(qū)(x=0.9～1.5)，潤滑應(yīng)力存在明顯二次應(yīng)力峰，其寬度較窄，潤滑應(yīng)力隨后急劇下降(圖4a)。而隨著速度增加或載荷減小都會使二次應(yīng)力峰提前出現(xiàn)。

(3)在潤滑應(yīng)力分布的二次應(yīng)力峰相對應(yīng)位置處，油膜厚度開始收縮，在出口區(qū)形成油膜頸縮現(xiàn)象，當(dāng)運行速度增加或載荷減小時，都會使得油膜頸縮位置提前。

此外，從圖中還可以觀察到，軸箱軸承的運行速度及滾子載荷對潤滑應(yīng)力和油膜厚度分布有明顯影響，因此，需要分析軸箱軸承潤滑性能的影響因素。

3 潤滑性能的影響因素

3.1 輪軸變形

軸箱系統(tǒng)多界面接觸行為研究表明，輪軸軸頸變形導(dǎo)致軸箱軸承滾子承載不均勻。v=120 km/h時，軸頸變形對軸箱軸承潤滑性能的影響如圖6所示。

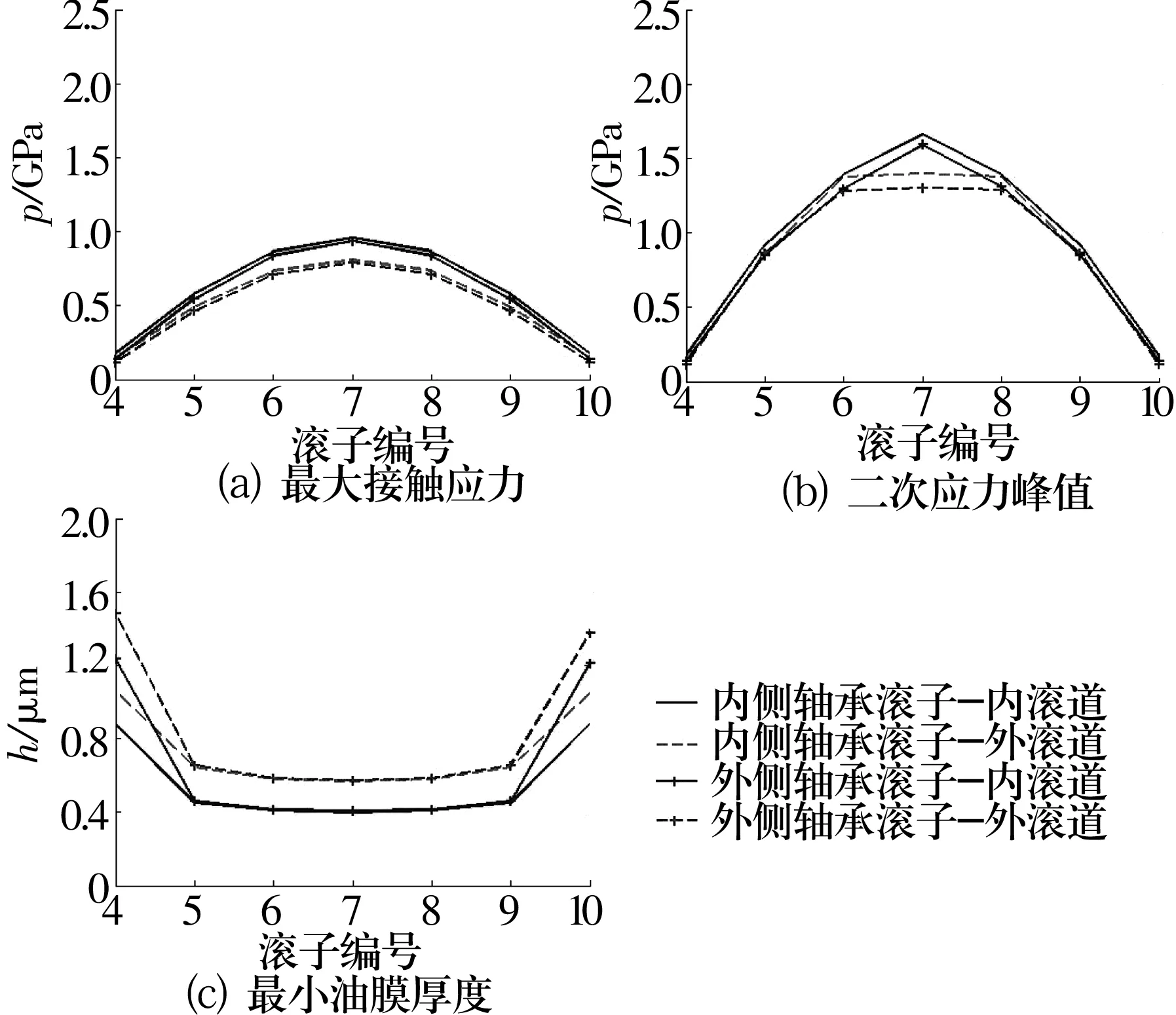
圖6 輪軸軸頸變形對潤滑性能的影響

由圖6可知，軸頸變形雖然會導(dǎo)致內(nèi)、外側(cè)滾道接觸載荷產(chǎn)生一定的非均勻性分布，但對滾子與滾道間最大潤滑應(yīng)力和最小油膜厚度影響不大。

3.2 運行速度

不同運行速度下，軸箱軸承滾子與滾道間的潤滑應(yīng)力分布和最小油膜厚度分布如圖7～圖10所示。

圖7 不同速度下內(nèi)側(cè)軸承滾子與內(nèi)滾道間的潤滑應(yīng)力分布

圖8 不同速度下外側(cè)軸承滾子與外滾道間的潤滑應(yīng)力分布

圖9 不同速度下內(nèi)側(cè)軸承最小油膜厚度的分布

圖10 不同速度下外側(cè)軸承最小油膜厚度的分布

由圖可知，不同運行速度下滾子與滾道接觸面的潤滑應(yīng)力分布十分接近。隨著運行速度的提高，最大潤滑應(yīng)力變化不明顯，二次應(yīng)力峰值隨之增大，同時油膜厚度也會增加，有助于形成良好的潤滑狀態(tài)。另外，運行速度對滾子與內(nèi)滾道間潤滑應(yīng)力的影響比滾子與外滾道間的要大，滾子與外滾道接觸面的潤滑性能要優(yōu)于滾子與內(nèi)滾道。

3.3 載荷

分析圖9、圖10可知，隨著滾子承受載荷的增大，滾子與滾道接觸面的最大潤滑應(yīng)力增大，油膜厚度減小，主承載區(qū)滾子的油膜厚度分布比較平緩，與非承載區(qū)的分布情況不同。因此，需要進一步分析載荷對軸承潤滑性能的影響規(guī)律。

鐵路客車軸箱系統(tǒng)的動態(tài)行為可以導(dǎo)致軸承載荷幅值發(fā)生較大的變化，實際工況下產(chǎn)生的動載荷可以達到正常載荷的1～5倍。產(chǎn)生的動載荷或沖擊載荷對軸箱軸承潤滑應(yīng)力及油膜厚度分布有十分顯著的影響，直接影響軸箱軸承的壽命和可靠性。因此，在軸承設(shè)計制造、安裝及服役上，需要考慮載荷變化對軸箱軸承潤滑性能的影響[12]。以表2中承載最大的7#滾子接觸載荷Q7的1～5倍進行計算分析，v=120 km/h時，7#滾子與內(nèi)、外滾道接觸時的潤滑應(yīng)力及油膜厚度分布如圖11、圖12所示。

圖11 載荷變化對滾子與內(nèi)滾道間潤滑性能的影響

圖12 載荷變化對滾子與外滾道間潤滑性能的影響

由圖可知，滾子接觸載荷越大，最大潤滑應(yīng)力越大，且其分布越趨近于Hertz分布形式，最大潤滑應(yīng)力也越接近于二次應(yīng)力峰值，即潤滑應(yīng)力重載區(qū)域由二次應(yīng)力峰處向Hertz應(yīng)力分布段轉(zhuǎn)移，潤滑應(yīng)力重載區(qū)域增大。

滾子接觸載荷增大導(dǎo)致最小潤滑油膜厚度減小。接觸載荷越大，中心油膜厚度與最小油膜厚度越小，整個油膜厚度減小，容易導(dǎo)致滾子與滾道間潤滑失效，進入邊界潤滑狀態(tài)，摩擦力將快速增大，導(dǎo)致溫升增大，進而發(fā)生熱軸等危險現(xiàn)象。

因此，載荷增大將導(dǎo)致最大潤滑應(yīng)力及內(nèi)、外滾道上的最大潤滑應(yīng)力差增大；同時，導(dǎo)致相應(yīng)的最小油膜厚度及內(nèi)、外滾道上的最小油膜厚度差減小。以上行為將減弱潤滑性能，極易導(dǎo)致潤滑狀態(tài)進入邊界潤滑，從而引起潤滑失效等問題。

鐵路軸箱軸承系統(tǒng)大規(guī)模接觸潤滑模擬系統(tǒng)的建立, 有助于鐵路提速客車軸箱軸承的微尺度設(shè)計、制造技術(shù)以及服役技術(shù)識別與發(fā)展，為鐵路提速客車軸箱軸承產(chǎn)品的發(fā)展提供有效的技術(shù)支持和發(fā)展基礎(chǔ)[12-13]。

4 結(jié)論

(1)軸箱輪軸撓曲會引起軸箱內(nèi)、外側(cè)軸承滾道接觸載荷分布不均，但對滾子與滾道間最大潤滑應(yīng)力和最小油膜厚度影響不大，滾子與內(nèi)滾道接觸面的潤滑性能較滾子與外滾道的差。

(2)隨著鐵路客車運行速度的提高，最小油膜厚度的增大有利于形成良好的潤滑。但運行速度對潤滑性能影響的差異不大。

(3)隨著動態(tài)接觸載荷的增大，軸承潤滑性能明顯降低，故須考慮載荷變化對軸箱軸承潤滑性能的影響。