滾動軸承振動速度的乏信息真值估計

栗永非，時保吉

（新鄉職業技術學院，河南 新鄉 453006）

振動特性是滾動軸承的動態性能之一，對主機的動態性能、工作壽命及可靠性等有重大影響，其可以綜合、全面反映軸承產品的整體質量水平［1-2］。為了從總體上把握軸承振動的基本特性，需要對軸承振動參數的真值進行評估。由于軸承振動特性具有乏信息特征，使得軸承振動特性的真值估計成為難題。目前，學者們已經研究了許多真值評估方法，如最大似然法［3-4］、最大后驗估計［5-7］、加權平均法［8］和最小二乘逼近等［9］，但這些通常都是基于大樣本條件下進行的。為此，提出基于小樣本的真值融合方法，該方法是對滾動平均法、隸屬函數法、最大隸屬度法、滾動自助法和算術平均法的多次融合。在此基礎上，提出了乏信息條件下基于多個估計真值的融合方法的點估計，通過對圓錐滾子軸承的質量參數進行蒙特卡洛（Monte Carlo）模擬和試驗研究，以驗證文中所述融合方法的適應性和有效性。

1 真值融合模型

為解決乏信息系統的真值估計問題，采用多種數學方法進行研究，進而從多個側面獲取整個系統的屬性信息。當方法不同時，評判準則各異，就會得到不同的屬性信息。將獲得的屬性信息構成集合，就是所謂的估計真值集合。該集合從多個方面描述系統的屬性特征，通過融合得到的屬性信息，能更合理地對系統屬性真值進行估計，即真值融合技術。

設系統輸出的軸承質量數據序列為

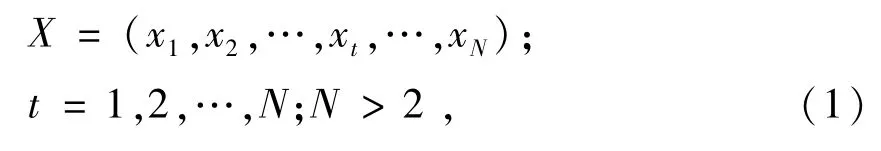
式中：xt為原始序列X中的第t個數據；N為數據的個數。

1.1 真值融合方法

由于研究的軸承質量數據序列概率分布未知且數據量很小，提出以下5種真值估計方法。

1.1.1滾動均值法

將（1）式中的數據由小到大排列，則

1.1.2 隸屬函數法

作為一種定量融合方法，隸屬函數法實際屬于加權均值方法，權重即為隸屬函數fi。

1.1.3 最大隸屬度法

依據隸屬函數法，設最大隸屬度為

1.1.4 滾動自助法

設軸承質量數據序列X為

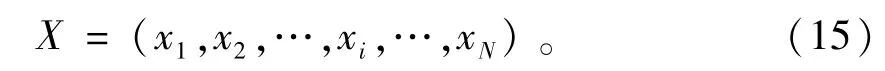
從序列X中進行自助抽樣，等概率可放回地抽取mD＝N個數據，則獲得自助樣本Xb，連續抽取B次，就能夠得到B個自助樣本

將自助樣本從小到大排序，并分為Q組，就可以得到各組的組中值Xmq和概率密度函數f（x）或離散頻率Fq，q＝1，2，…，Q。

以頻率Fq為權重，則估計真值為

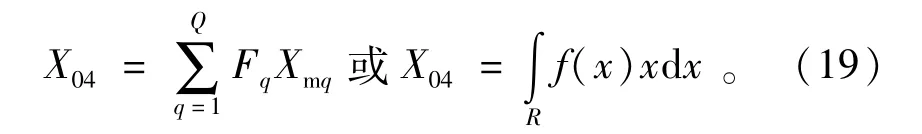
1.1.5 算術平均法

算術平均法是第5種真值估計方法，是最常用的點估計方法之一。

定義系統的估計真值為

1.2 估計真值的融合

采用多種數學方法得到估計真值的解集X0后，將X0作為第0次融合序列，表示為

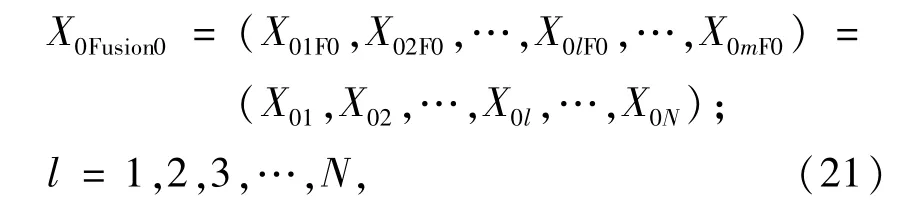
式中：X0l為采用第l種數學方法得到的真值的估計結果。

然后采用所提出的融合方法對X0Fusion0進行計算，得到第1次融合序列

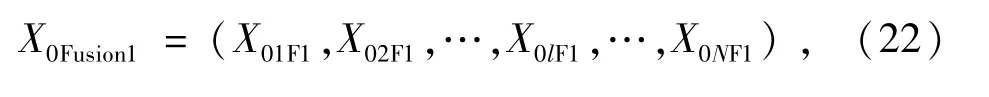
式中：X0lF1為采用第l種數學方法對第0次融合序列融合的計算結果。

依此類推，第k次融合序列為

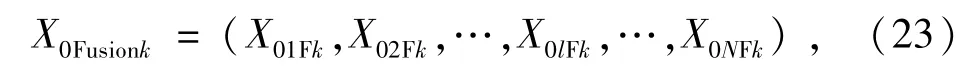
式中：X0lFk為對采用第l種數學方法對第k-1次融合序列融合的計算結果。

定義3：存在任意小的實數ε，若極差滿足

式中：N為第k-1次融合序列融合計算結果的個數。此準則稱為極差準則。

1.3 約定真值

根據誤差理論和統計理論，如果差異很小，基于大樣本的5個估計真值可以被認為是接近數學期望EM的，故可以被視為約定真值Xtrue，即

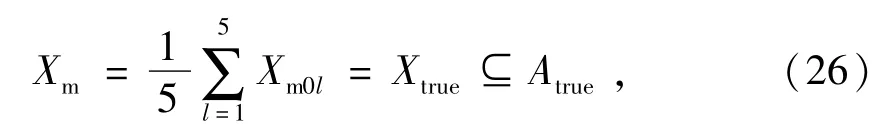
式中：Xm為5個真值的平均值；Xtrue為約定真值；Atrue為系統屬性的真值集合。

2 試驗研究

試驗對象為30204圓錐滾子軸承，隨機抽取30套軸承，利用B1010振動儀采集軸承徑向振動速度信號（包括低頻、中頻和高頻）。圖1所示為軸承振動數據序列。需進行5個測試系列的試驗研究，其中每個測試序列有30個數據。

圖1 軸承振動數據序列

2.1 大樣本條件下的約定真值

如上所述，平均值Xm可用于描述大樣本條件下的約定真值Xtrue。在此基礎上，將30個數據作為測試樣本，即Ntest＝30，則分別采用5種真值融合方法計算出5個估計真值，結果見表1。

表1 軸承振動速度在大樣本N test＝30下的估計真值

由表1可知，在大樣本條件下軸承低頻、中頻和高頻速度的5個估計真值差別均很小，最大相對誤差分別為1.2%，2.2%和0.7%，則5個估計真值的平均值即為低、中、高頻振動速度的約定真值Xtrue，即低頻XmL＝197.7μm／s＝XLtrue，中頻XmM＝169.7μm／s＝XMtrue，高頻XmH＝84.9 μm／s＝XHtrue。

2.2 小樣本條件下軸承振動速度的評估

從圖1中分別選取低、中、高頻振動速度測試序列的前5個數據，即小樣本個數N＝5，形成新的測試序列X，

低頻XL＝（262，180，202，195，225），

中頻XM＝（202，150，128，172，165），

高頻XH＝（90，98，120，75，90）。

采用上述5種融合方法，基于小樣本的軸承振動速度估計真值及與約定真值的相對誤差見表2。

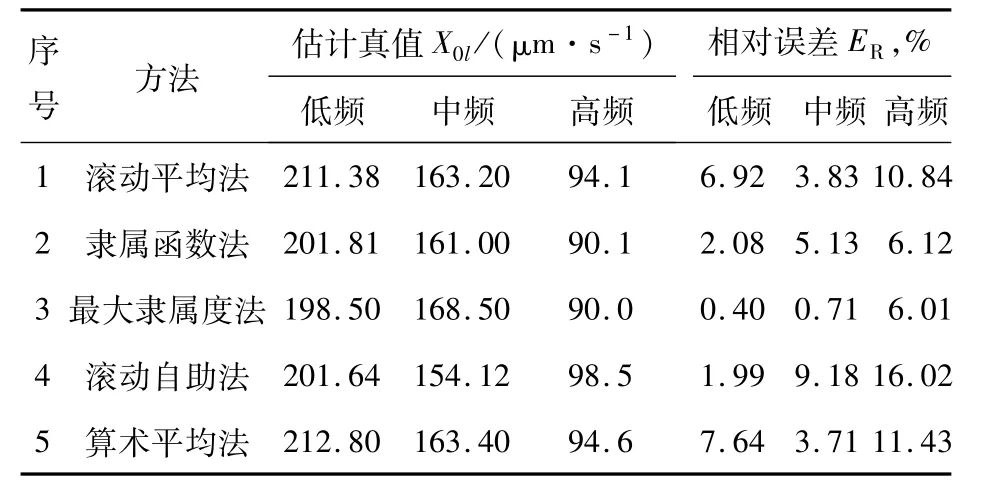
表2 小樣本條件下振動速度的估計真值（N＝5）

從表2可以看出，在小樣本條件下，這5種方法得到的估計真值有明顯不同，與約定真值的相對誤差也很大。

根據誤差理論對有效數據的控制原理，分別采用滾動平均法、隸屬函數法、最大隸屬度法、滾動自助法和算術平均法對對低頻、中頻和高頻振動估計真值進行3次融合，結果見表3。

表3 軸承振動速度的估計真值的融合序列（N＝5）

取ω＝0.5，根據極限準則，最終估計真值見表4。

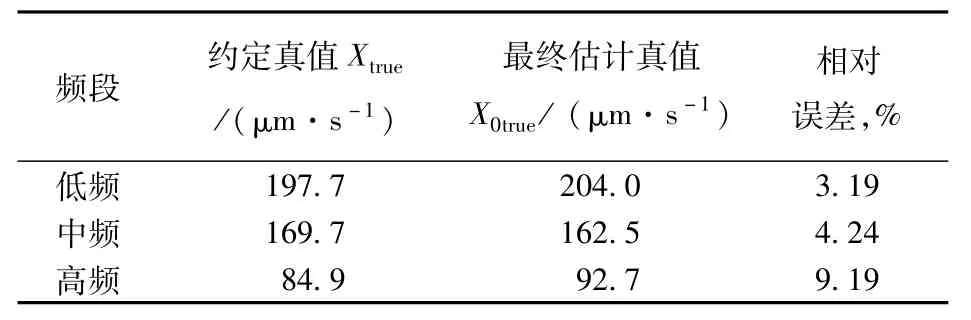
表4 小樣本條件下的最終估計真值（N＝5）

3 Monte Carlo仿真

采用Monte Carlo法模擬任意概率分布（本文為均勻分布）的隨機過程，區間為［0，1］，則得到隨機過程的測試序列Xtrue（圖2），測試序列數據個數為Ntest＝1 024。顯然，測試序列服從均勻分布。根據統計理論，均勻分布的數學期望為0.5，則測試序列的約定真值為U＝0.5μm／s。

圖2 基于Monte Carlo仿真的均布測試序列（N test＝1 024）

從圖1中選取測試序列的前5個數據，即小樣本個數N＝5，形成新的測試序列X＝（0.773 74，0.406 97，0.724 49，0.557 77，0.387 96）。

采用上述方法，基于小樣本的Monte Carlo仿真均布估計真值見表5。從表5很容易看出，這5種方法得到的估計真值明顯不同，其與約定真值U的最大相對誤差為20.51%，最小相對誤差為10.62%。

表5 基于小樣本的均布估計真值（N＝5）

對均布估計真值進行融合，結果見表6，取ε＝0．005，根據極限準則，最終估計真值為

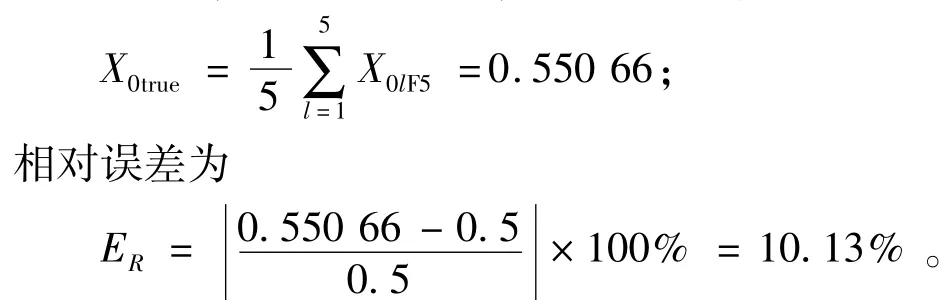
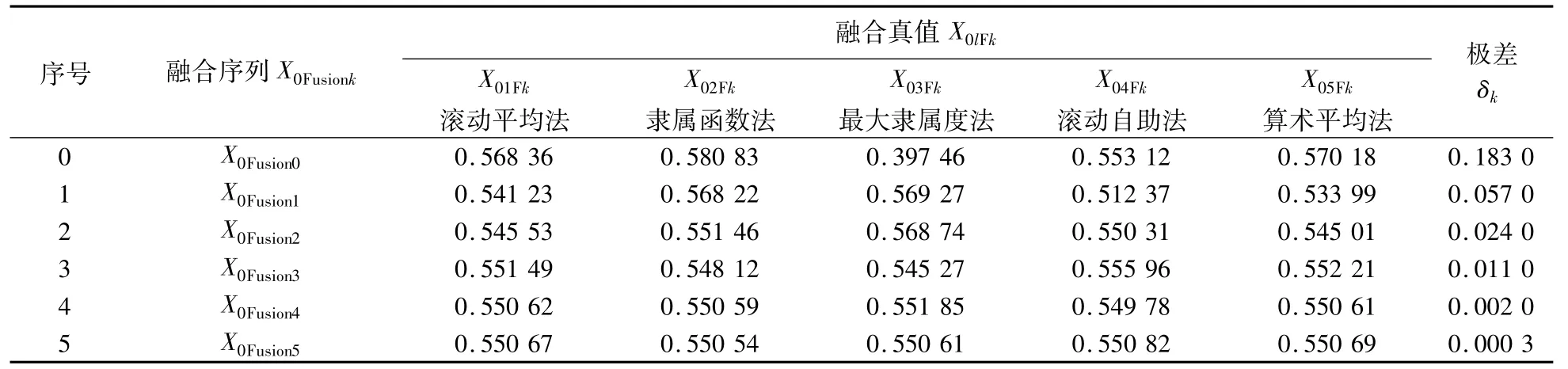
表6 均勻分布估計真值的融合序列

為便于觀察，將這4個測試序列最后的結果總結于表7中，由表可知，在小樣本條件下，傳統估計真值和最終估計真值的相對誤差范圍為3.19%～10.13%。采用融合方法進行多次融合后，最大相對誤差為10.13%，而采用單一方法的最大誤差則達20.51%。

4 結束語

建立了真值融合模型，并通過圓錐滾子軸承振動試驗研究證明，基于小樣本的真值融合模型具有更高的評估精度，最大相對誤差僅有9.19%，誤差較小；而采用單一方法得到的最大相對誤差通常較大。

通過Monte Carlo仿真進一步證明了真值融合模型評估的有效性，真值融合方法對于解決小樣本和概率分布未知的問題具有可靠的估計結果。