關于2015年高考新課標Ⅰ卷理綜第25題解法的探究

賀慧鴿 段姜維

（武功縣綠野高級中學 陜西 咸陽 712209）

2015年高考結束，對于新課標Ⅰ卷理綜，縱觀全卷，題目難易程度適中，較全面地考查了大綱所要求的知識點.關于計算題第25題，由于試題所給答案較為繁瑣，本文現提出以下不同解答方式，以供各位同仁共同學習討論.

【原題】一長木板置于粗糙水平地面上，木板左端放置一小物塊；在木板右方有一墻壁，木板右端與墻壁的距離為4.5m，如圖1（a）所示.t＝0時刻開始，小物塊與木板一起以共同速度向右運動，直至t＝1 s時木板與墻壁碰撞（碰撞時間極短）.碰撞前后木板速度大小不變，方向相反；運動過程中小物塊始終未離開木板.已知碰撞后1s時間內小物塊的v－t圖線如圖1（b）所示.木板的質量是小物塊質量的15倍，重力加速度大小g取10m／s2.求：

（1）木板與地面間的動摩擦因數μ1及小物塊與木板間的動摩擦因數μ2；

（2）木板的最小長度；

（3）木板右端離墻壁的最終距離.

圖1

解法1：（試題所給解法）

（1）規定向右為正方向.木板與墻壁相碰前，小物塊與木板一起向右做勻變速運動，設加速度為a1，小物塊和木板的質量分別為m和M.由牛頓第二定律有

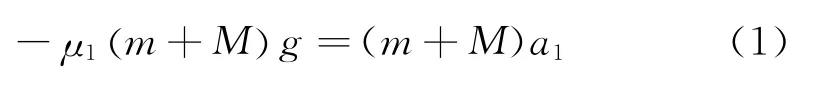
由圖可知，木板與墻壁碰前瞬間的速度v1＝4 m／s，由運動學公式得

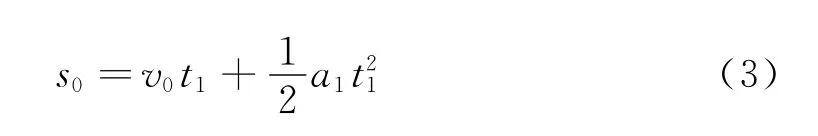
式中，t1＝1s，s0＝4.5m 是木板碰前的位移，v0是小物塊和木板開始運動時的速度.聯立式（1）～（3）和題給條件得

在木板與墻壁碰撞后，木板以－v1的初速度向左做勻變速運動，小物塊以v1的初速度向右做勻變速運動.設小物塊的加速度為a2，由牛頓第二定律有

由圖可得

式中，t2＝2s，v2＝0，聯立式（5）、（6）和題給條件得

（2）設碰撞后木板的加速度為a3，經過時間Δt，木板和小物塊剛好具有共同速度v3.由牛頓第二定律及運動學公式得

碰撞后至木板和小物塊剛好達到共同速度的過程中，木板運動的位移

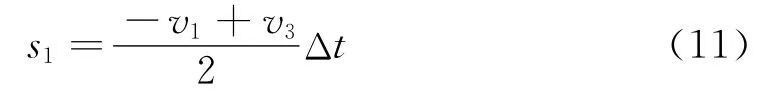
小物塊運動的位移

小物塊相對木板的位移

聯立式（6）和式（8）～ （13），并代入數值得

因為運動過程中小物塊沒有脫離木板，所以木板的最小長度應為6.0m.

（3）在小物塊和木板具有共同速度后，兩者向左做勻變速運動直至停止，設加速度為a4，此過程中小物塊和木板運動的位移為s3.由牛頓第二定律及運動學公式得

碰后木板運動的位移為

聯立式（6）、（8）～ （11）、（15）～ （17），并代入數值得

木板右端離墻壁的最終距離為6.5m.

本文所給解法如下.

解法2：圖像法

（1）規定向右為正方向.木板與墻壁相碰前，小物塊與木板一起向右做勻減速運動，設加速度為a1.對木板，由圖1（b）可知，碰撞瞬間木板速度為4m／s，即木板和小物塊一起勻減速運動的末速度為4m／s，時間t1＝1s，位移為4.5m，對小物塊和木板系統，根據逆向思維可得

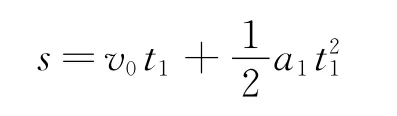
可得a1＝1m／s2（方向向左），而a1＝μ1g，則μ1＝0.1.

對小物塊，直接由圖像可得碰后a2＝－4m／s2，而a2＝μ2g，故μ2＝0.4.

（2）木板碰撞墻壁后，小物塊的加速度a2＝－4 m／s2，設此時木板的加速度為a3，由牛頓第二定律有

由于μ1＝0.1，a2＝－4m／s2μ2＝0.4，所以可求得

設經過時間t2小物塊和木板達到共同速度v，則

代入數據，解得t2＝1.5s，v＝－2m／s.

作出木板和墻壁碰撞后的速度圖像如圖2所示，根據圖像可知小物塊和木板的相對位移

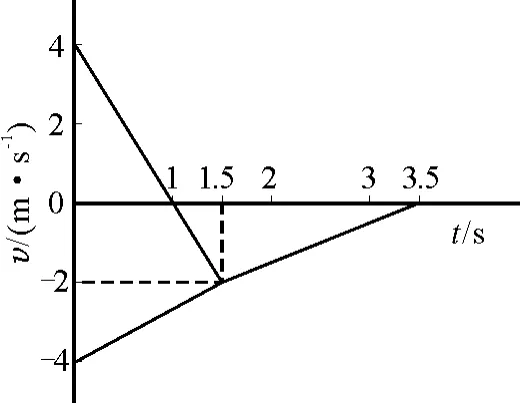
圖2

（3）在小物塊和木板具有共同速度后，兩者向左做勻減速運動直至停止，設加速度為a4.由牛頓第二定律得

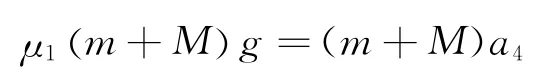
代入數據可知

設經過時間t3，二者速度減為零，由運動學公式

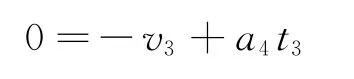
可知t3＝2s.

作出圖像，如圖2所示，根據圖像可知，木板右端離墻壁的最終距離為

解法3：

（1）略.

（2）根據解法2的有關數據可知小物塊相對木板滑動前的初速度v1＝4m／s，最后二者共同向左勻減速的速度v2＝2m／s，由動能定理，對小物塊有

得

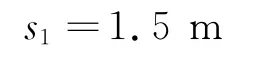
對木板有

得

所以木板長度

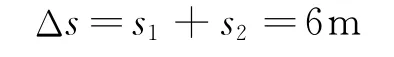
（3）對整個系統，從碰后到停止運動，根據動能定理，有

代入數據，得