基于信息論的KL-Reg點云配準算法

秦紅星徐 雷

(重慶郵電大學計算智能重慶市重點實驗室 重慶 400065)

(重慶郵電大學計算機科學與技術學院 重慶 400065)

基于信息論的KL-Reg點云配準算法

秦紅星*徐 雷

(重慶郵電大學計算智能重慶市重點實驗室 重慶 400065)

(重慶郵電大學計算機科學與技術學院 重慶 400065)

針對含有高噪聲、體外點及不完整點云數據的配準失效問題，該文提出以信息論為理論基礎，相對熵度量點云相似度的KL-Reg算法。該算法不需要顯式地建立對應關系，首先將點云數據建模為高斯混合模型，然后用相對熵度量高斯混合模型間的分布距離，最后通過最小化分布距離計算模型變換。實驗結果表明所提的KL-Reg算法配準精度高、穩定性強。

機器視覺；點云配準；KL散度；高斯混合模型

1 引言

點云數據配準是計算機視覺和計算機圖形學中的重要研究內容，是3維重建、圖像配準[1]和3維形狀檢索[2,3]的核心技術，其主要目的是尋找一個模型變換以實現兩幅點云的對齊。點云配準過程面臨許多挑戰。首先，數據本身存在的高噪聲、體外點等會影響配準精度；其次，在3維數據采集過程中，由于掃描儀的視角和自遮擋問題，獲得的數據經常存在缺失或者只有少部分重合等問題。使得尋找點到點的對應關系變得非常困難，并由于點云間對應不準確往往造成配準失效。另外，點云數據的初始位置也會影響配準算法的性能。

目前的點云配準算法主要分為3類：迭代最近點配準算法ICP(Iterate Closed Point)[4,5]、基于統計的方法和基于特征對應的配準方法。1992年Besl和McKay提出了ICP[4]算法，該方法以歐式距離最近的點對作為對應點對，思想簡單、易于實現是最常用的點云配準算法。但是ICP算法依賴對應關系[6]，對兩幅點云的初始距離比較敏感。2013年Tagliasacch等人[5]提出稀疏迭代最近點算法(sparse iterative closet point)，該算法在配準含噪聲和體外點的點云數據時可以保持很好的魯棒性，但當兩幅點云距離較遠時，配準的效果仍不理想。為了解決ICP算法對噪聲敏感問題，基于統計的配準方法[7?11]被相繼提出。Myronenko等人[8]提出的CPD (Coherent Point Drift)算法，基本思想是先通過E步確定對應概率，根據對應概率建立似然函數，再通過M步最大化似然函數計算變換模型。不同于ICP算法中對應點是一對一的關系，這類方法用概率建立兩幅點云之間的軟對應(多對多)關系。另一類基于特征的配準算法[12?17]一般是通過特征匹配建立點對的對應關系，其中Lombaert 等人[16]提出的方法根據點的熱核坐標[18,19]尋找對應點。雖然特征方法在計算線性變換時的性能優良，但需要大量的計算資源而且同樣會面臨特征對應不準確的問題。

上述3類方法存在的缺點是當對應缺失或者對應不準確時，會嚴重影響配準結果。本文提出的基于信息論的KL-Reg配準算法，不需要建立顯式的對應關系，解決了由于對應不準確造成的配準失效問題。與Jian[8]和CPD算法[9]相比本文方法不需要優化高斯混合模型中的每一個高斯組件的權值。

2 KL-Reg算法思想

設點云M, S都是從一個實體對象采樣獲得的兩幅點云數據，p(x|S,r), p(x|M,w)表示點云S, M的采樣模型分布，配準S, M，就是使它們的分布模型盡可能相似。本節內容包括：點云數據的分布模型表達；用信息理論中的KL散度度量分布距離的方法；最后是如何最小化距離目標函數計算映射變換。

2.1 點云數據的模型表達

點云模型是由大量的散亂點混合在一起，設這些散亂點獨立同分布，則可用高斯分布來建立點云分布模型。文獻[8]把點云中的每一個點表達為一個單高斯模型(組件)，點云M的高斯混合模型表達為p(x|M)其中mj為M中第j的坐標，為第j個點的高斯分布，wj為第j個組件的權值，, δ為高斯核函數的寬度，N為M中

M點的數量。

假設點云中的每一個點都是以相同的概率從一個高斯混合模型隨機采樣獲得，則每一個高斯組件的權值是相同的，設wj=1/NM。為了對噪聲和體外點建模，高斯混合模型中增加一個額外的統一采樣分布p(x|M')=1/NM表示噪聲和體外點。假定點云M, S都是從一個實體對象采樣獲得的數據，則兩個高斯混合模型的高斯核寬度相同，噪聲比例相同。加入噪聲后M的高斯混合模型可表達為

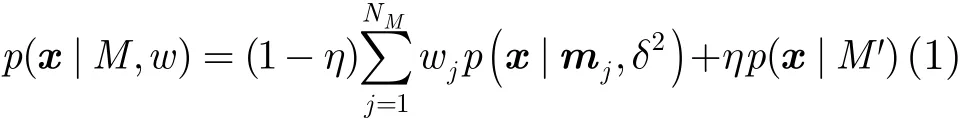
其中0≤p(x|mj)≤1,wj=1/NM, η表達點云中噪聲點所占比重。同理點云S的高斯混合模型可表達為

其中0≤p(x|si)≤1,

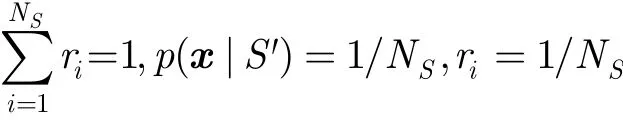
當兩幅點云距離越近時，其模型相似度就越高。因此配準的目標可以描述為，尋找一個模型變換T，使點云M經過該變換后與點云S的模型分布距離最小。

2.2 高斯混合模型的相似性度量

我們采用相對熵度量點云M和點云S分布的相似程度。Hershey等人[20]論證了度量高斯混合模型KL散度的可行性，因此保證了本文算法的有效性。設f(x)和g(x)為D維空間中的兩個分布函數，其KL散度定義為

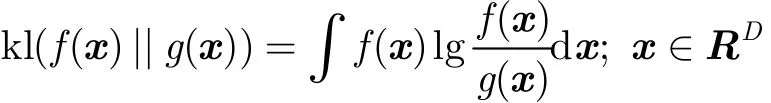
由KL散度的性質可知：當密度函數f(x)=g(x)時，kl(f(x)||g(x))=0；當f(x)與g(x)的差異越大，kl(f(x)||g(x))值越大。兩幅點云的模型分布距離為kl(p(x|S,r)||p(x|M,w))。因此配準問題可表達為

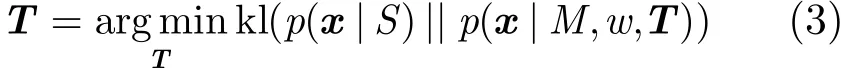
2.3 目標函數優化

我們通過優化兩個分布模型距離的上界間接優化式(3)目標函數，分布函數f(x),g(x)的KL散度可轉化為

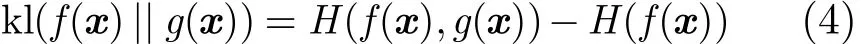
其中H(f(x),g(x))為f(x)和g(x)的交叉熵，H(f(x))為f(x)的信息熵。根據Hershey的方法[20]，式(4)的上界可表示為

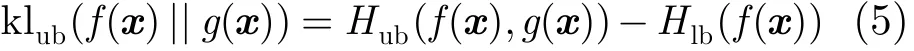
其中klub(f(x),g(x))表示式(4)的上界，Hup(f(x), g(x))為H(f(x),g(x))上界，Hlb(f(x))為H(f(x))的下界。令f(x)=p(x|S,r ),g(x)=p(x|M,w,T)則有

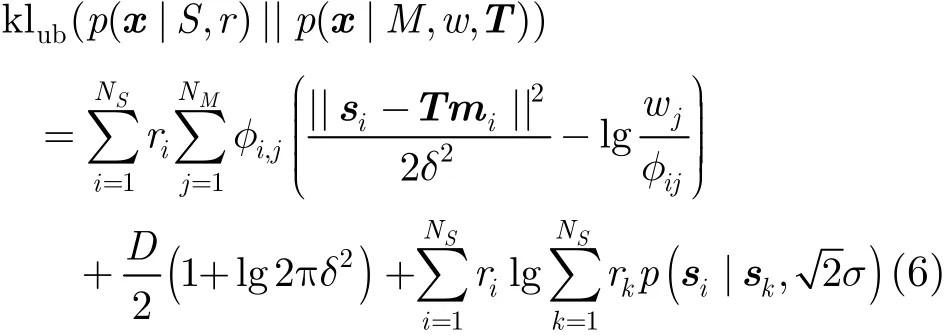
其中

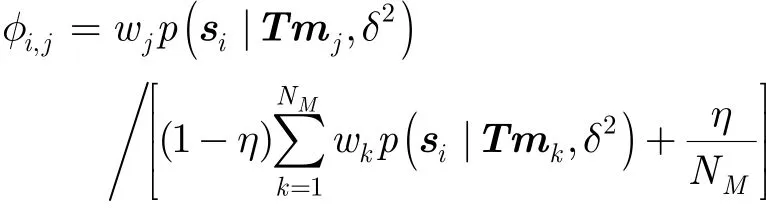
優化問題轉化為求解式(1)上界，即式(6)來求解變換參數。當2δ確定時，上述目標函數可化為

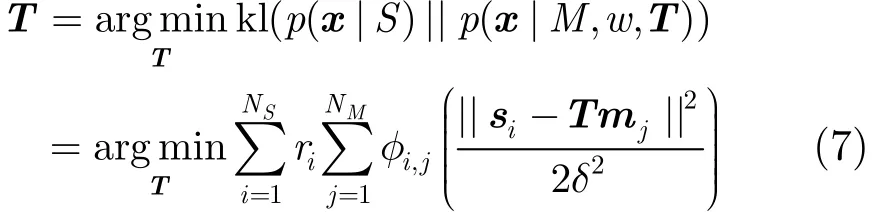
式(7)目標函數是機器視覺領域中常見的優化問題，可以通過梯度下降法[9]來解決。高斯函數的寬度δ的選擇是上述優化問題收斂的關鍵。本文2δ的選取采取自適應的方法，令

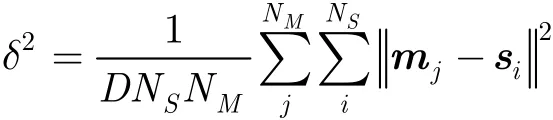
在每次迭代中，點云M經過模型變換后同時調整δ2。事實上可以將δ2等同于模擬退火算法中的溫度，即隨著迭代次數的增大，參數δ2逐漸減小。另外當點云之間旋轉角度較大時，算法往往會陷入局部最優，當迭代次數達到迭代的上限并且δ2仍然未收斂到時，即認為配準失敗。收斂閾值的大小取決于對配準時間和配準精度的要求，實驗表明閾值越小配準的精度越高，但配準的時間就越長。本文結合蟻群算法[21]的思想，當迭代次數達到一個閾值，并且算法不收斂時就選擇一個比較差的解，重新迭代。實驗表明一般經過兩次調整后即可找到全局最優解。

3 實驗結果與分析

本文算法用Matlab實現，硬件平臺為2.5 GHz Intel CPU, 2G內存空間。實驗包括2維點云和3維點云配準實驗以及定量對比實驗。為了與其他方法[8]的實驗結果進行對比，本文采用文獻[8]中使用的數據和3維掃描儀的掃描數據進行配準實驗。配準實驗收斂閾值取為10?8，調整解空間的迭代次數為30次。

3.1 2維點云配準實驗

圖1為KL-Reg算法與CPD算法[8]配準2維魚形點云[22]的對比實驗，圖1(a), 1(b), 1(c)為點云的初始分布，圖1(d),1(e),1(f)為CPD算法的配準結果，圖1 (g),1(h),1(i)為KL- Reg算法的配準結果。實驗結果表明CPD算法配準圖1 (b)中數據時不能得到全局最優解，文獻[7]的算法對2維魚形點云可適應的旋轉弧度范圍為[?2.0, 2.0]。本文根據蟻群算法[21]的思想，自動調整解空間，一般經過兩次調整后就能找到全局最優解，實驗表明KL-Reg算法可適應的旋轉角度范圍為[?π, π]。

圖1(c),1(f),1(i)為數據不完整時的配準實驗，當點云數據只有部分重合或者點云數據不完整時往往難以建立準確的對應關系，從而造成配準失敗。實驗結果表明，KL-Reg算法在對應不準確時仍然可以準確地配準點云，算法穩定性強。

圖1(a), 1(d), 1(g)為配準含噪聲和數據不完整點云時的實驗，圖1 (d), 1(g)分別為CPD算法和KL-Reg算法配準結果。在配準此類數據時，KL-Reg算法比CPD算法的配準結果更準確。

3.2 3維點云配準實驗

圖2數據為斯坦福掃描的中國龍點云數據[23]，采集中國龍點云時兩個掃描儀夾角分別為24°，圖2(a), 2(d)分別為從正面和背面觀察兩幅點云的初始位置。圖2(b), 2(e)為CPD算法配準的結果，圖2(c), 2(f)為KL-Reg算法配準結果。可以發現，圖2(b), 2(e)采用CPD算法配準的結果中龍頭處存在較大誤差，而KL-Reg算法取得了較好的配準結果(圖2(c), 2(f))。

3.3 量性對比實驗

為了更加詳盡地驗證KL-Reg算法的有效性，本文與ICP[4], CPD[8], KC-Reg[9]和EM-ICP[10]算法進行了實驗對比，配準數據為2維魚形點云。對比實驗包括：配準含不同比例噪聲點云時各個算法的配準時間和誤差；配準不完整點云數據時各個算法的配準誤差。圖3中配準時間單位為s，誤差計算公式為

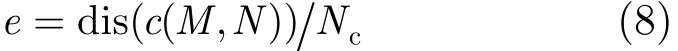
其中dis(c(M,N))為配準后兩幅點云中對應點的距離和函數，Nc為對應點的個數。

表1為各個算法在配準數據不完整點云時的配準誤差。實驗結果表明KL-Reg算法的配準誤差一直穩定在10?16左右，并不會隨噪聲比例的增加而增加，而CPD算法的配準誤差對不完整點云數據比較敏感。KC-Reg算法、EM-ICP算法和ICP算法的配準誤差會隨噪聲的比例遞增而遞增，其中ICP算法的配準誤差遞增的速度最快。圖3為配準含不同比例噪聲數據的時間對比，ICP算法的配準時間最短，雖然KL-Reg算法時間復雜度與CPD算法相當，而配準誤差一直保持穩定，說明KL-Reg算法要比CPD算法魯棒性更高。

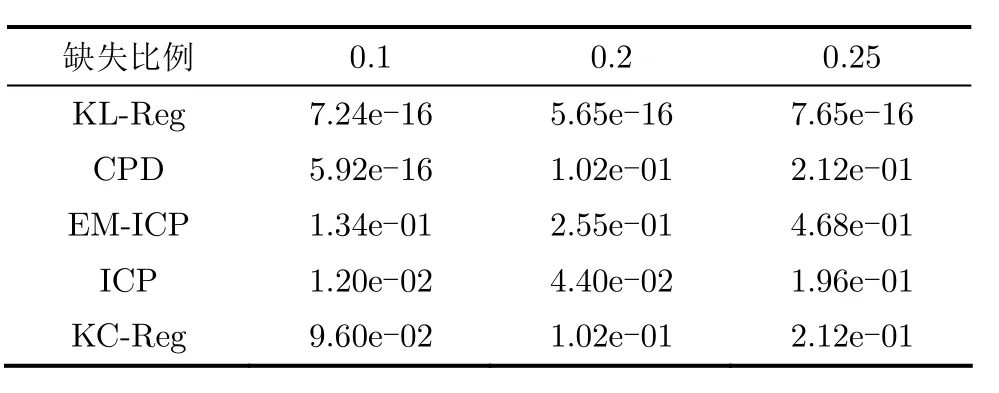
表1 數據缺失時的配準誤差

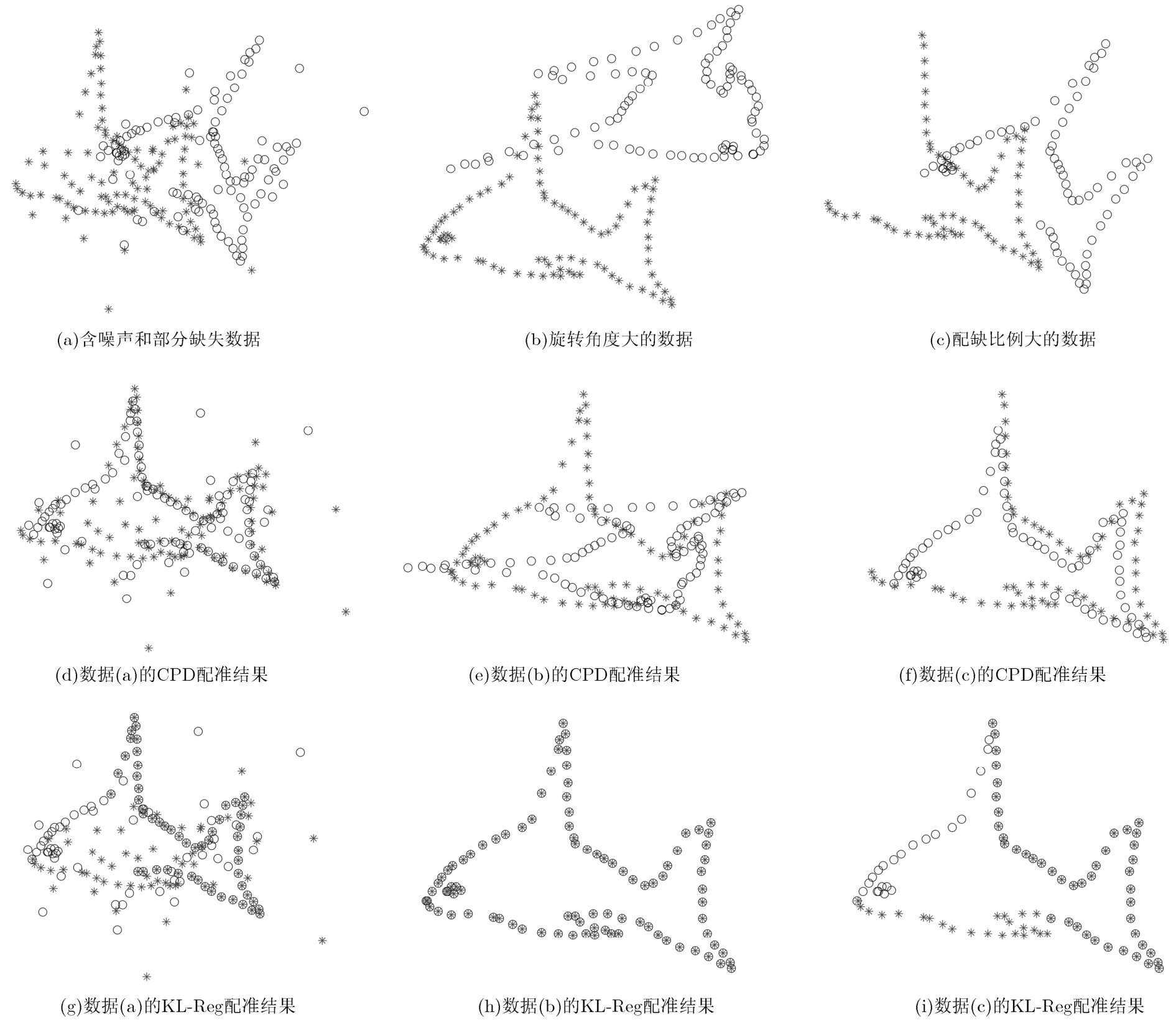
圖1 2維魚形點云配準實驗

圖2 中國龍3維點云配準實驗

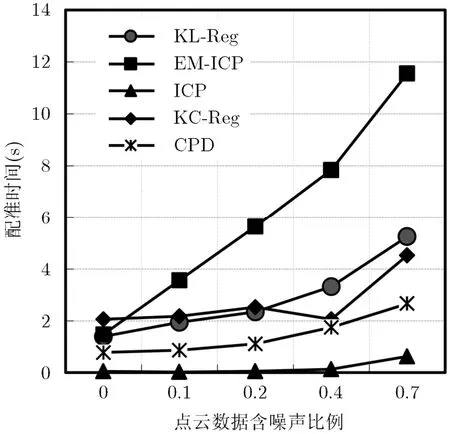
圖3 含噪聲點云數據配準時間對比

4 結束語

針對配準含有高噪聲、體外點點云及不完整點云數據時，由于難以找到準確的對應關系導致的配準失效問題。本文提出的基于信息論的KL-Reg點云配準算法，提高了在對應關系不準確時配準的有效性和穩定性。KL-Reg算法認為點云從一個實體對象表面采樣獲得，且存在一個共同的采樣分布，那么配準后的兩幅點云應該符合這個采樣分布，因此配準的過程描述為兩個采樣分布的擬合過程。與文獻[7]和文獻[8]CPD算法相比，本文方法不需要優化高斯混合模型中的每一個高斯組件的權值，本文基于總體分布的思想更為簡單，易于實現。最后與ICP[4], CPD[8], KC-Reg[9]和EM-ICP[10]算法的實驗表明，本文算法不僅能夠精確配準點云，而且在配準不完整點云及有噪聲點云時魯棒性更高。

[1] Zitova B and Flusser J. Image registration methods: a survey[J]. Image and Vision Computing, 2003, 21(11): 977-1000.

[2] Lian Z, Godil A, Bustos B, et al.. A comparison of methods for non-rigid 3D shape retrieval[J]. Pattern Recognition, 2013, 46(1): 449-461.

[3] Liu M, Vemuri B C, Amari S I, et al.. Shape retrieval using hierarchical total bregman soft clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(12): 2407-2419.

[4] Besl P J and McKay N D. Method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 586-606.

[5] Tagliasacchi A, Bouaziz S, and Pauly M. Sparse iterative closest point[J]. Computer Graphics Forum, 2013, 32(5): 113-123.

[6] Tam G K L, Cheng Z Q, Lai Y K, et al.. Registration of 3D point clouds and meshes: a survey from rigid to nonrigid[J]. IEEE Transactions on Visualization and Computer Graphics, 2013, 19(7): 1199-1217.

[7] Jian B and Vemuri B C. Robust point set registration using gaussian mixture models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1633-1645.

[8] Myronenko A and Song X. Point set registration: coherent point drift[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262-2275.

[9] Tsin Y and Kanade T. A correlation-based approach to robust point set registration[C]. Computer Vision-ECCV 2004. Springer Berlin Heidelberg, Prague, 2004: 558-569.

[10] Granger S and Pennec X. Multi-scale EM-ICP: a fast and robust approach for surface registration[C]. Computer Vision—ECCV 2002, Springer Berlin Heidelberg, Copenhagen, 2002: 418-432.

[11] Hermans J, Smeets D, Vandermeulen D, et al.. Robust point set registration using EM-ICP with information-theoretically optimal outlier handling[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado, USA, 2011: 2465-2472.

[12] Lipman Y, Yagev S, Poranne R, et al.. Feature matching with bounded distortion[J]. ACM Transactions on Graphics, 2014, 33(3), DOI: 10.1145/2602142.

[13] Paulus S, Dupuis J, Mahlein A K, et al.. Surface feature based classification of plant organs from 3D laserscanned point clouds for plant phenotyping[J]. BMC Bioinformatics, 2013, 14(1), DOI: 10.1186/147-2105-14-238.

[14] Zeng Y, Wang C, Gu X, et al.. A generic deformation model for dense non-rigid surface registration: a higher-order MRF-based approach[C]. IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 2013: 3360-3367.

[15] Hou T and Qin H. Robust dense registration of partial nonrigid shapes[J]. IEEE Transactions on Visualization and Computer Graphics, 2012, 18(8): 1268-1280.

[16] Lombaert H, Grady L, Polimeni J R, et al.. FOCUSR: feature oriented correspondence using spectral regularization?a method for precise surface matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, Australia, 2013, 35(9): 2143-2160.

[17] Chang W and Zwicker M. Automatic registration for articulated shapes[J]. Computer Graphics Forum, 2008, 27(5): 1459-1468.

[18] Bronstein M M and Kokkinos I. Scale-invariant heat kernel signatures for non-rigid shape recognition[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, 2010: 1704-1711.

[19] Sun J, Ovsjanikov M, and Guibas L. A concise and provably informative multi-scale signature based on heat diffusion[J]. Computer Graphics Forum, 2009, 28(5): 1383-1392.

[20] Hershey J R and Olsen P A. Approximating the Kullback Leibler divergence between Gaussian mixture models[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, 2007(4): 317-320.

[21] Karaboga D, Gorkemli B, Ozturk C, et al.. A comprehensive survey: artificial bee colony (ABC) algorithm and applications[J]. Artificial Intelligence Review, 2014, 42(1): 21-57.

[22] Chui Hai-li. Point matching[OL]. http://www.cise.ufl.edu /～anand/students/chui/research.html. 2014.5.

[23] Stanford computer graphics laboratory. 3Dscanrep[OL]. http://graphics.stanford.edu/data/3Dscanrep/. 2014.5.

秦紅星： 男，1978年生，教授，主要研究方向為計算機圖形學與可視化.

徐 雷： 男，1989年生，碩士生，研究方向為計算機圖形學.

Information Theory Based KL-Reg Point Cloud Registration

Qin Hong-xing Xu Lei
(Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China)
(College of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China)

The registration of point clouds with high noises, outliers and missing data will be failure because the correspondence between point clouds is inaccurate. This paper proposes a information theory based point cloud registration method called KL-Reg algorithm without building correspondence. The method represents the point cloud with Gaussian mixture model, then computes the transformation through minimizing the KL divergence without build explicit correspondence. Experimental results show that KL-Reg algorithm is precise and stable.

Machine vision; Point clouds registration; KL-divergence; Gaussian mixture model

TP391

： A

：1009-5896(2015)06-1520-05

10.11999/JEIT141248

2014-09-25收到，2015-02-27改回

國家自然科學基金青年科學基金(61100113)，國家教育部留學歸國基金教外司留[2012]940號，重慶市首批青年骨干教師項目(渝教人(2011)31號)，重慶市基礎與前沿研究計劃項目(cstc2013jcyjA 40062)，重慶郵電大學學科引進人才基金(A2010-12)和重慶市研究生科研創新項目(CYS14142)資助課題

*通信作者：秦紅星 qinhx@cqupt.edu.cn