基于高斯混合勢化概率假設密度的脈沖多普勒雷達多目標跟蹤算法

吳衛華江 晶馮 訊劉重陽

(空軍預警學院 武漢 430019)

基于高斯混合勢化概率假設密度的脈沖多普勒雷達多目標跟蹤算法

吳衛華*江 晶馮 訊劉重陽

(空軍預警學院 武漢 430019)

為在新興的隨機有限集(RFS)框架下充分利用多普勒信息跟蹤雜波環境下的多目標，該文提出基于高斯混合勢化概率假設密度(GM-CPHD)的脈沖多普勒雷達多目標跟蹤(MTT)算法。該算法在標準GM-CPHD基礎上，在使用位置量測更新狀態后，再利用多普勒量測進行序貫更新，可獲得更精確的似然函數和狀態估計。仿真結果驗證了該算法的有效性，表明在GM-CPHD基礎上引入目標的多普勒信息可有效抑制雜波，顯著改善跟蹤性能。

多目標跟蹤；隨機有限集；概率假設密度；高斯混合勢化概率假設密度；脈沖多普勒雷達

1 引言

現代機載預警雷達普遍采用脈沖多普勒體制，如何更好地利用機載脈沖多普勒雷達獲取的多普勒觀測進行多目標跟蹤具有重要意義。

傳統基于數據關聯的多目標跟蹤算法，如S維(S-Dimensional, S-D)分配算法，聯合概率數據關聯(Joint Probabilistic Data Association, JPDA)，多假設跟蹤(Multiple Hypothesis Tracking, MHT)等，由于數據關聯步驟的運算復雜度較高，難以勝任大規模的目標數目及其狀態均具有時變性質的實時多目標跟蹤問題。近年來，一類基于隨機有限集(Random Finite Sets, RFS)的跟蹤算法[1,2]應運而生，受到跟蹤界的極大關注。

在傳統算法中，多普勒信息對跟蹤性能的改善一直備受重視[3]。在隨機有限集框架下，文獻[4]考慮到多普勒盲區的影響，通過建模檢測概率為目標狀態的函數，獲得了更穩定的目標數目估計。不過，該算法僅利用了與多普勒盲區有關的最小可檢測速度(Minimum Detectable Velocity, MDV)信息，并未利用多普勒信息。文獻[5]基于高斯混合概率假設密度[6](Gaussian Mixture Probability Hypothesis Density, GM-PHD)研究了利用多普勒信息進行航跡起始及雜波抑制的問題。然而，在PHD濾波器中，由于泊松分布的均值與方差相等，因此，當目標數目較多時，在漏檢或較高虛警密度下，會造成目標數目估計的強起伏，使得估計不可靠[7]。文獻[7]提出的勢化概率假設密度(Cardinalized Probability Hypothesis Density, CPHD)濾波器較好地克服了該問題，具有比PHD更優的性能，其已擴展到可適用于航跡形成[8,9]、未知出生強度[10,11]、時變雜波密度[12]、傳感器配準[13]和分布式融合結構[14,15]條件下。然而，尚未有文獻在GM-CPHD框架下引入多普勒信息來改善跟蹤性能，為此，本文研究在更為復雜的CPHD式子中引入多普勒信息的問題，提出了基于GM-CPHD的脈沖多普勒雷達多目標跟蹤算法。通過仿真驗證了算法的有效性，結果表明，多普勒信息的引入可有效抑制雜波干擾，顯著改善跟蹤精度。

2 多目標濾波問題的RFS描述

考慮x-y平面內多目標跟蹤場景。在k?1時刻，存在M(k?1)個目標，它們的狀態為Xk?1,1, Xk?1,2,…,Xk?1,M(k?1)∈χ。在下一時刻，現存目標可能消失或者繼續存活，新的目標可能出現或者由現有目標衍生出來，上述過程得到M(k)個新狀態Xk,1,Xk,2,…,Xk,M(k )，其中，Xk,i=[xk,iyk,i]T。假定k時刻傳感器接收到N(k)個量測zk,1,zk,2,…, zk,N(k)∈Z，其中僅有部分量測來自于目標，其余為虛警或雜波。由于k時刻對應的目標狀態集合以及量測集合的無序性，它們可自然地用有限集合表示：

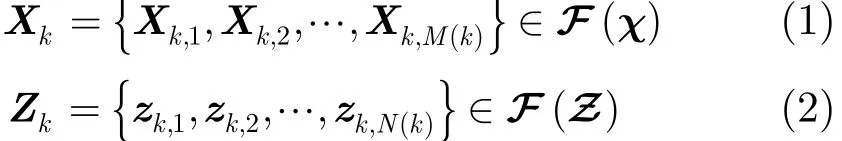
其中，F(χ)與F(Z)分別是χ與Z的所有有限子集的集合。

給定k?1時刻多目標狀態Xk?1，則k時刻的多目標狀態Xk由存活目標和新生目標的集合的并集給出。

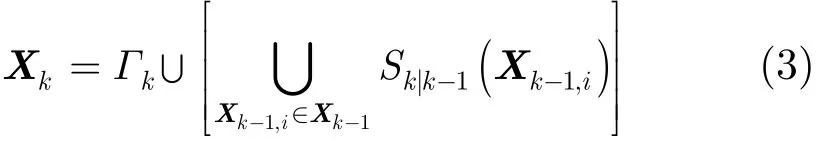
其中，Γk代表k時刻新生目標的RFS。Γk的實際形式取決于具體問題。Sk|k?1(Xk?1,i)是k時刻存活目標由Xk?1,i演化而來的目標RFS，每一Xk?1,i∈Xk?1要么以概率pS,k(Xk?1,i)繼續存在，或者以概率1?pS,k(Xk?1,i)消失。假定目標存在概率與狀態無關，即

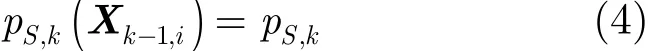
以目標存在為條件，從狀態Xk?1,i轉移到Xk,i的概率密度函數(Probability Density Function, PDF)為

式中，N(?;m,P)表示均值m和協方差P的高斯密度，Fk?1為狀態轉移矩陣，Qk?1為過程噪聲協方差。

給定多目標狀態Xk，傳感器接收的多目標量測Zk可由目標產生的量測和雜波的并集表示

其中，Kk為雜波的RFS，其實際形式與具體問題有關；Θk(Xk,i)表示檢測到的目標量測RFS，當目標以檢測概率pD,k(Xk,i)被檢測時，Θk(Xk,i)取{zk,j}中某元素，否則，當以概率1?pD,k(Xk,i)漏檢時，Θk(Xk,i)為?。假定檢測概率與狀態不相關，即

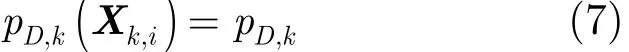
以檢測到目標為條件，觀測zk,j來自于狀態Xk,i的量測方程為

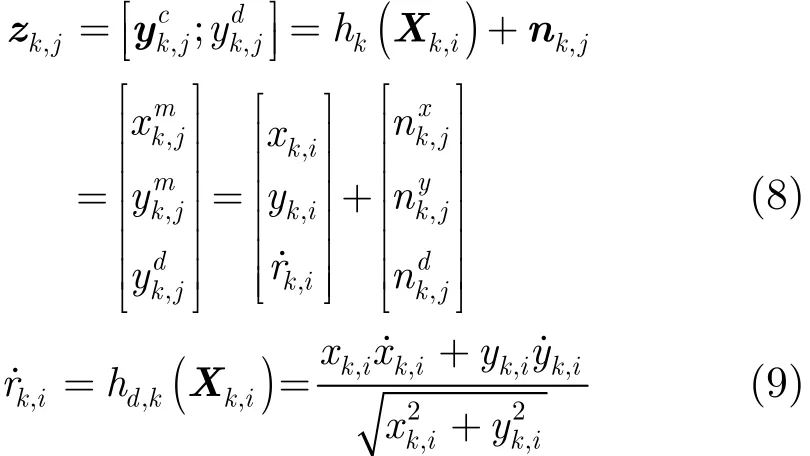
其中，nk,j～N(nk,j;0,Rk)為均值0，協方差Rk=的高斯白噪聲(假定多普勒噪聲與位置噪聲相互獨立)。,分別表示位置觀測與多普勒觀測值，它們的似然函數分別為

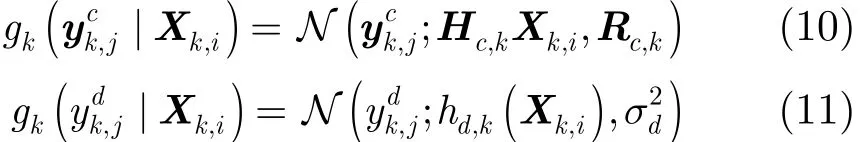
其中，Hc,k=diag(I2,02)為位置觀測矩陣，In,0n分別表示n×n的單位矩陣和全零矩陣。

3 帶Doppler量測的序貫GM-CPHD算法

假定每個目標運動過程及產生的量測獨立，預測的多目標RFS服從泊松分布，雜波也服從泊松分布，并與目標量測獨立，新生目標的RFS的強度為高斯混合形式：

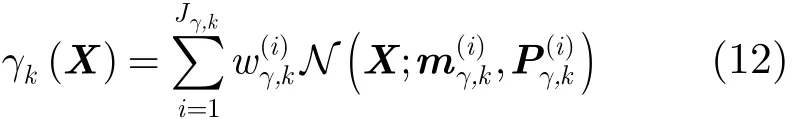
其中，Jγ,k為出生強度分量數目，權值、均值、協方差,i=1,2,…,Jγ,k是給定的模型參數，它們共同決定出生強度的形狀。

給定k?1時刻的后驗勢分布pk?1及高斯混合形式的后驗強度υk?1為

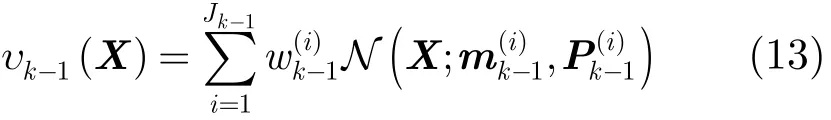
則k時刻的預測勢分布pk|k?1及預測強度υk|k?1分別為[7]

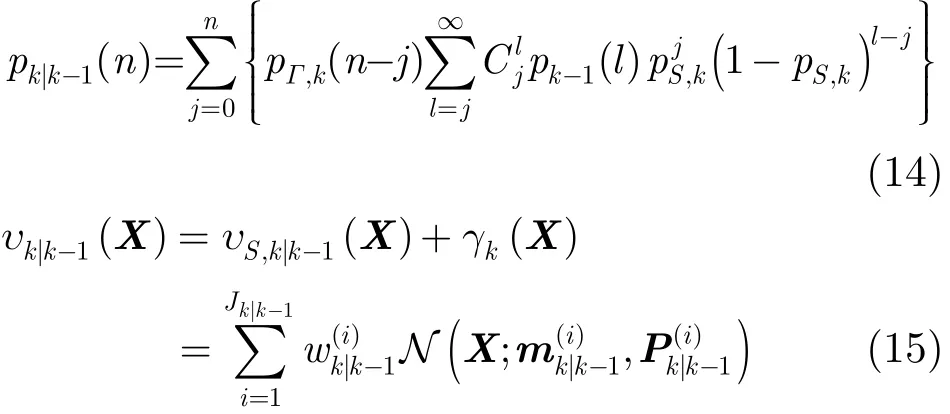
獲取k時刻觀測后，可得更新后驗勢分布和強度函數分別為[7]

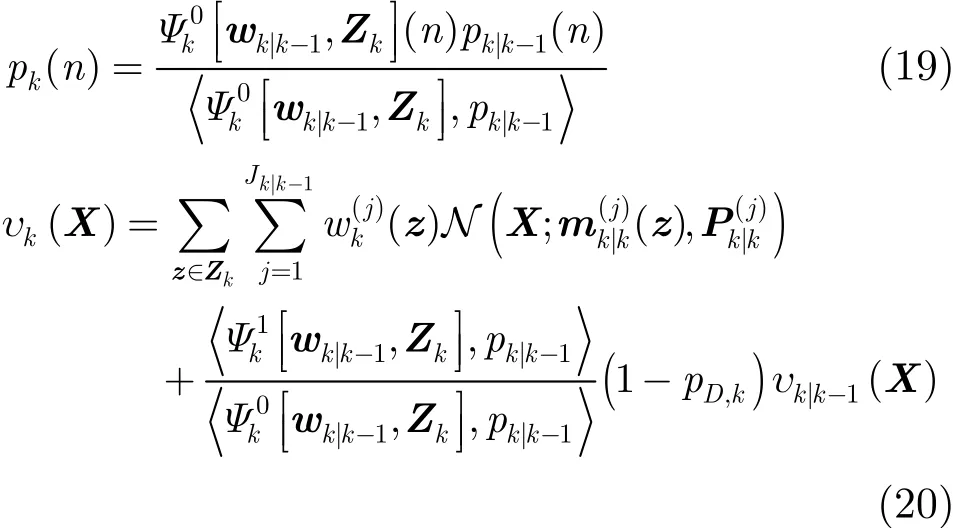
為在GM-CPHD濾波器中并入多普勒信息，可采取位置和多普勒量測聯合濾波或位置和多普勒量測序貫濾波方法，為更有效地利用多普勒信息，這里采用后者，即，首先利用位置量測進行狀態更新，接著使用多普勒量測進一步更新狀態，在得到更精確的狀態估計和似然函數后，最后利用位置和多普勒量測信息計算權重。算法具體步驟為：

其中

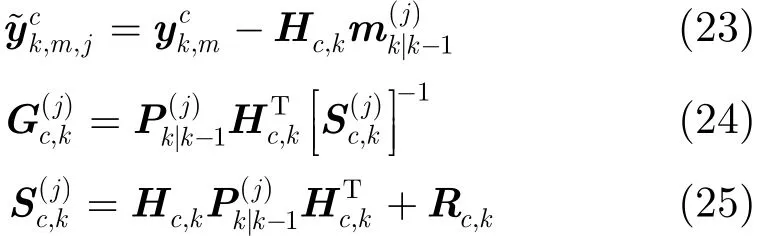
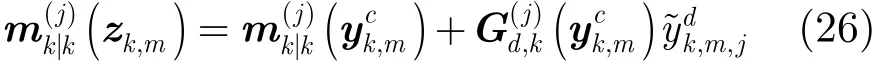
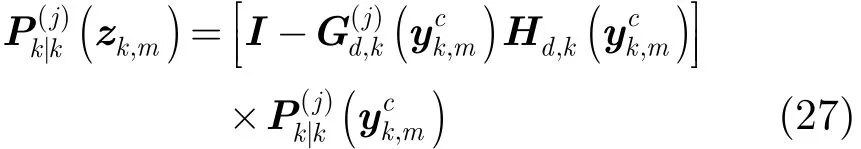
其中

式中

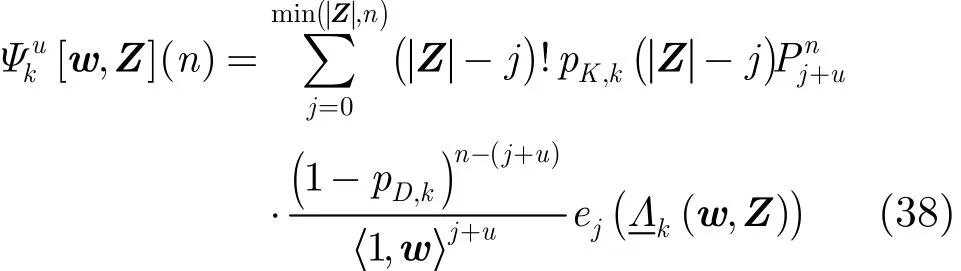
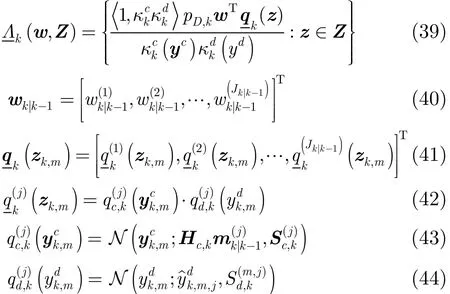
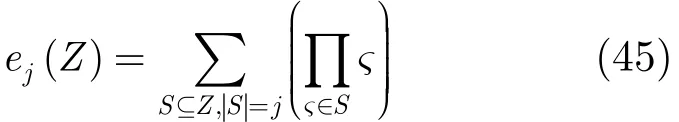
4 仿真實驗與分析

考慮到本文側重多目標跟蹤的研究，不妨假定多目標在x-y平面內做勻速直線運動。設定目標的初始狀態及其起始、終止時間見表1。傳感器監視區域[?1000 m 1000 m]×[?1000 m 1000 m]，對應面積V=4×106m2，假定pD,k=0.98,Rc,k=I2, σc=10m,σd=0.5 m/s ,vmax=35 m/s2。在GMPHD和GM-CPHD濾波器中，pS,k=0.99, Fk?1=, Δ=1 s, σv=5m/s。新生目標出生強度設計為m= [0 m,0 m,0 m/s,0 m/s]T, m=[400 m,?600 m,0 m/s,0 m/s]T, m=[?200 m,800 m,0 m/s,0 m/s]T, m=[?800 m,?200 m,0 m/s,0 m/s]T,Jγ,k=4, w=0.03, P=diag([10 m2,10 m2,10 m2/s?2,10

m2/s?2]T),i=1,2,3,4。狀態提取過程中用到的合并參數[6]有：權值門限T=10?5，合并門限U=4，最大高斯分量數目Jmax=100。GM-CPHD中勢分布近似截取參數[7]Nmax=100。

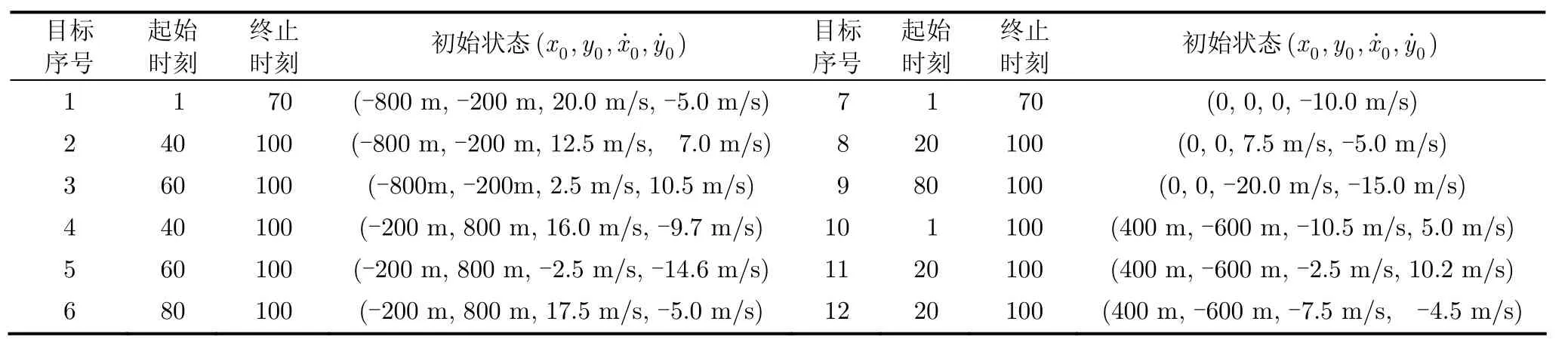
表1 各目標初始狀態及其起始、終止時間

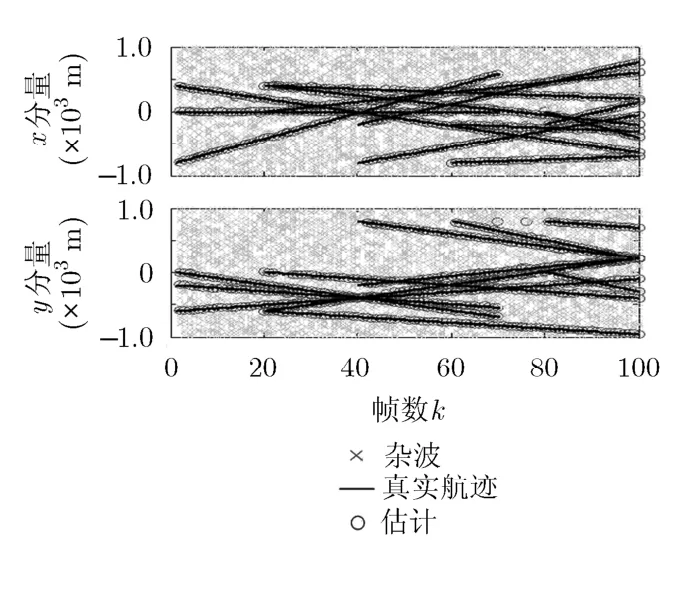
圖 1 GM-CPHDwD算法多目標跟蹤典型結果

圖 2 不同時刻下GM-CPHDwD算法跟蹤性能

為驗證GM-CPHDwD中引入多普勒信息對雜波抑制和性能改善的能力，分別記不帶Doppler信息的標準GM-PHD[6]和GM-CPHD[7]算法為GMPHDwoD和GM-CPHDwoD，以及文獻[5]提出的帶多普勒信息的GM-PHD算法為GM-PHDwD。圖3給出了4種算法在λc=0,0.25×10?5m?2,…,1.50 ×10?5m?2不同雜波密度條件下的OSPA總誤差，以及OSPA中勢估計誤差和定位誤差[16](對應的雜波平均數目為0,10,…,60)。總體而言，多普勒信息的引入對GM-PHD和GM-CPHD均顯著改善了性能，且雜波密度越高，性能改善越為明顯，表明多普勒信息的利用可有效抑制雜波干擾；相比GMPHDwD，圖3(a)說明GM-CPHDwD在定位精度上稍差，但圖3(b)表明其在勢估計性能上又優于GMPHDwD，從而，從整體OSPA角度而言，GMCPHDwD優于GM-PHDwD，見圖3(c)。

5 結束語

為在新興的隨機集框架下充分利用多普勒信息，本文提出了基于GM-CPHD的機載多普勒雷達多目標跟蹤算法，仿真結果證明了該算法的有效性，表明利用多普勒信息可有效抑制雜波干擾，顯著改善跟蹤性能。下一步工作是研究在多普勒盲區條件下的基于隨機有限集的機載多普勒雷達多目標跟蹤算法。

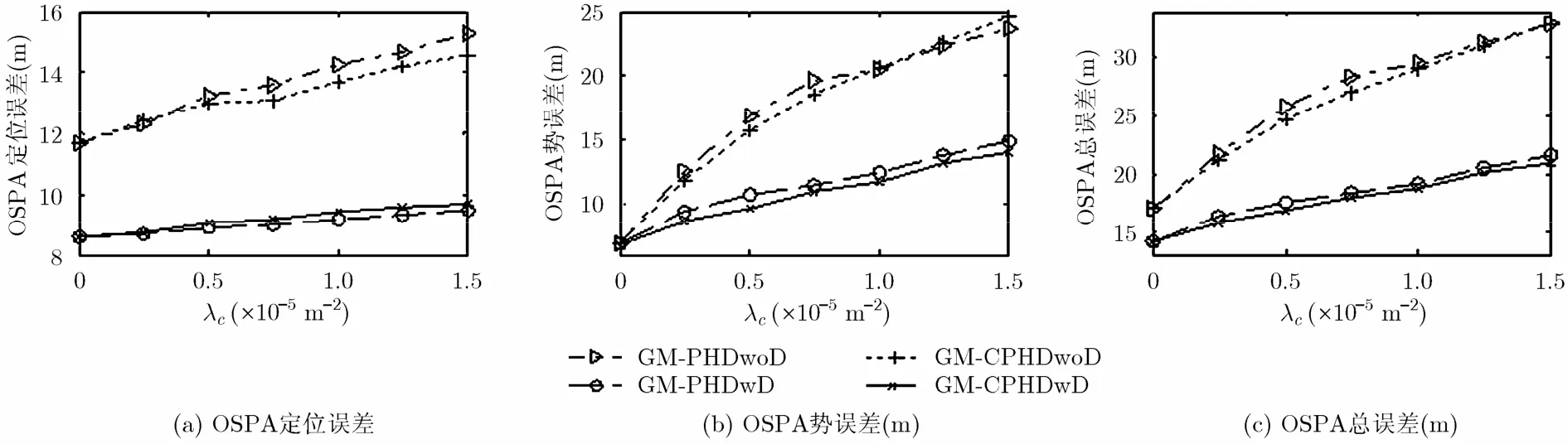
圖 3 不同雜波密度下各算法跟蹤性能比較

[1] Mahler R. Statistical Multisource-multitarget Information Fusion[M]. Norwood: Artech House, 2007.

[2] Reuter S, Wilking B, Wiest J, et al.. Real-time multi-object tracking using random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2666-2678.

[3] Zhou G, Pelletier M, Kirubarajan T, et al.. Statically fused converted position and Doppler measurement Kalman filters[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 300-318.

[4] Ulmke M, Erdinc O, and Willett P. GMTI tracking via the Gaussian mixture cardinalized probability hypothesis density filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1821-1833.

[5] Yoon J H, Kim D Y, Bae S H, et al.. Joint initialization and tracking of multiple moving objects using Doppler information[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3447-3452.

[6] Vo B-N and Ma W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.

[7] Vo B T, Vo B N, and Antonio C. Analytic implementations of the cardinalized probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.

[8] Ouyang C, Ji H, and Tian Y. Improved Gaussian mixture CPHD tracker for multitarget tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1177-1191.

[9] 歐陽成, 姬紅兵, 張俊根. 一種改進的CPHD多目標跟蹤算法[J]. 電子與信息學報, 2010, 32(9): 2112-2118. Ouyang C, Ji H, and Zhang J. Improved CPHD filter for multitarget tracking[J]. Journal of Electronics & Information Technology, 2010, 32(9): 2112-2118.

[10] Beard M, Vo B T, Vo B N, et al.. A partially uniform target birth model for Gaussian mixture PHD/CPHD filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2835-2844.

[11] Ristic B, Clark D, Vo B N, et al.. Adaptive target birth intensity for PHD and CPHD filters[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1656-1668.

[12] Beard M, Vo B-T, and Vo B-N. Multitarget filtering with unknown clutter density using a bootstrap GMCPHD filter[J]. IEEE Signal Processing Letters, 2013, 20(4): 323-326.

[13] Ristic B, Clark D, and Gordon N. Calibration of multi-target tracking algorithms using non-cooperative targets[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 390-398.

[14] Battistelli G, Chisci L, Fantacci C, et al.. Consensus CPHD filter for distributed multitarget tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 508-520.

[15] Uney M, Clark D, and Julier S. Distributed fusion of PHD filters via exponential mixture densities[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 521-531.

[16] Ristic B, Vo B-N, Clark D, et al.. A metric for performance evaluation of multi-target tracking algorithms[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3452-3457.

吳衛華： 男，1987年生，博士生，研究方向為多源信息融合.

江 晶： 男，1964年生，博士，教授，博士生導師，研究方向為現代信號處理、雷達數據處理、信息融合.

馮 訊： 男，1982年生，博士，研究方向為多傳感器數據融合.

劉重陽： 女，1988年生，博士生，研究方向為多傳感器組網.

Multi-target Tracking Algorithm Based on Gaussian Mixture Cardinalized Probability Hypothesis Density for Pulse Doppler Radar

Wu Wei-hua Jiang Jing Feng Xun Liu Chong-yang
(Air Force Early Warning Academy, Wuhan 430019, China)

In order to take full advantage of Doppler information for Multi-Target Tracking (MTT) in the clutter environment under the framework of emerging Random Finite Sets (RFS), an MTT algorithm based on Gaussian Mixture Cardinalized Probability Hypothesis Density (GM-CPHD) for pulse Doppler radar is proposed. Based on the standard GM-CPHD, the target states are updated sequentially using Doppler measurements after updating them using position measurements, then more accurate likelihood function and state estimation are obtained. Simulation results show the effectiveness of the proposed algorithm, and the introduced Doppler information can effectively suppress clutter and evidently improve tracking performance.

Multi-Target Tracking (MTT); Random Finite Sets (RFS); Probability Hypothesis Density (PHD); Gaussian Mixture Cardinalized Probability Hypothesis Density (GM-CPHD); Pulse Doppler radar

TN953

： A

：1009-5896(2015)06-1490-05

10.11999/JEIT141232

2014-09-23收到，2014-12-15改回

國家自然科學基金(61102168)資助課題

*通信作者：吳衛華 weihuawu1987@163.com