貝葉斯估計器先驗模型參數的迭代感知方法

鄒 鯤張 斌王曉薇林澄清

①(空軍工程大學信息與導航學院 西安 710077)

②(94816部隊 莆田 351100)

貝葉斯估計器先驗模型參數的迭代感知方法

鄒 鯤*①張 斌①王曉薇①林澄清②

①(空軍工程大學信息與導航學院 西安 710077)

②(94816部隊 莆田 351100)

充分利用先驗信息是提高統計推斷性能的有效途徑之一。貝葉斯估計的先驗信息模型參數必須在設計階段確定下來，與待探測環境模型參數之間必然存在不一致性，從而有可能導致估計質量的下降。該文首先給出了基于估計性能的先驗模型參數感知的一般性框架。基于該框架，針對白高斯噪聲中直流信號的貝葉斯估計器，分析了先驗失配條件下的估計性能，給出了一種先驗模型參數迭代感知的算法。利用計算機仿真分析了該估計器性能對先驗模型參數的敏感性和穩健性，分析了不同條件下的迭代感知過程。計算機仿真結果表明，該文給出的迭代感知方法建立了從估計性能到先驗模型參數的反饋，通過估計器與待探測場景的多次交互，可以使得先驗模型與當前場景模型匹配。

雷達信號處理；貝葉斯估計器；先驗模型失配；穩健性；敏感性；迭代感知方法

1 引言

在統計推斷中，可以使用總體信息和樣本信息。而在貝葉斯框架下，還可以使用先驗信息[1]。先驗信息主要來自經驗和歷史資料，是在統計推斷之前就必須確定下來的，具有一定的主觀性[2]。充分利用先驗信息，有助于提高統計推斷的質量。

對于雷達信息處理而言，合理使用先驗信息可以提高雷達目標的參數估計、檢測、跟蹤、識別性能[3]。利用先驗信息[4]，并建立合理的統計模型[5]，估計統計模型的參數[6]，并將這種帶有參數的先驗模型應用于雷達信號處理中。文獻[7]將雷達雜波的非高斯統計特性作為先驗信息，分析了雷達在嚴重拖尾復合高斯雜波中的探測性能，結果表明，先驗信息的使用可以提高雷達的探測能力。文獻[8]將雷達雜波協方差矩陣結構上的具有的反對稱性作為先驗信息，可以降低雷達自適應處理中對訓練數據數量的依賴程度。文獻[9]考慮了雜波協方差矩陣的先驗信息，可以提高雜波協方差矩陣的估計質量，甚至可以不需要訓練數據實現雜波協方差矩陣的估計[10]。文獻[11]利用探測環境的先驗信息提高了空時自適應處理中的雜波抑制能力。

需要指出的是，先驗信息只有與當前探測環境匹配時，才能提高雷達性能，先驗信息的不準確會導致雷達性能的下降。先驗信息通常在雷達處理器設計階段就必須給定，這使得先驗信息與當前探測環境必然存在不一致性。文獻[12]討論了海雜波非平穩性對雷達性能的影響，研究表明，雷達探測環境的復雜性以及先驗信息的不準確性會嚴重影響雷達的探測能力。文獻[13]研究了目標模型的不準確性帶來的檢測性能的影響，并給出了多種改進的檢測方法。唐波等人[14]也考慮到先驗信息的不準確性問題，給出了一種基于先驗知識定量評估的雜波協方差矩陣估計方法。鄒鯤等人[15]通過建立分層貝葉斯先驗模型，降低檢測器對先驗模型參數誤差的敏感性。

文獻[16]分析了先驗模型參數的失配與雷達檢測性能之間的量化關系，研究結果表明，在先驗模型失配條件下，雷達檢測性能會偏離標稱值，即檢測概率和虛警率與標稱值不一致。這種檢測性能與標稱值之間的差異實際上蘊含了先驗失配的信息，為此可以通過分析雷達在當前環境的檢測性能獲得先驗模型參數的感知[17]。目前針對認知雷達的研究多集中于目標跟蹤識別的范疇[18]，而對于信號的檢測與估計方面的研究較少[19]。檢測與估計是雷達信號處理中的核心問題，本文則是從信號估計的角度，分析先驗失配條件下估計器的性能，并探討先驗模型參數的感知方法。本文的創新之處在于從貝葉斯估計的角度，分析估計器性能與先驗模型參數失配之間的量化關系，建立了從估計器性能到先驗模型之間的反饋，構成了“利用先驗信息設計估計器，利用估計性能修正先驗模型”的認知閉環結構，通過多次的迭代過程實現先驗模型與待探測環境模型的匹配。需要指出的是，這種過程與常規的雷達自適應檢測估計或知識輔助方法有著較大的差異。雷達自適應檢測估計方法并不考慮先驗信息，雷達不具備對探測環境的理解能力。知識輔助方法雖然利用了先驗信息提高雷達探測性能，但并不考慮先驗模型的失配問題，以及對先驗模型更新問題。認知雷達利用了先驗信息提高探測能力的同時，還考慮到先驗信息是雷達對探測環境的學習過程。本文在第2節討論了基于估計性能的先驗模型參數感知的一般性框架，建立從估計性能到先驗模型參數的迭代感知過程。在第3節針對白高斯噪聲下的直流信號的估計問題，分析估計器在先驗失配條件下的性能，在第4節給出針對該估計器的先驗模型參數的迭代感知算法。在第5節利用計算機仿真分析先驗模型失配條件下的估計器性能，并分析多種條件下的先驗模型參數的迭代感知過程。最后給出全文的結論。

2 先驗模型參數感知的一般性框架

在貝葉斯框架下，利用數據x對某個參數a進行最小均方誤差估計時，將該參數看作隨機變量，并指定該參數的先驗分布作為其先驗模型。假定該參數為連續型隨機變量，其概率密度函數為fA(a;θ)，其中p維矢量θ是參數a的先驗分布參數。貝葉斯估計是參數a的后驗均值：

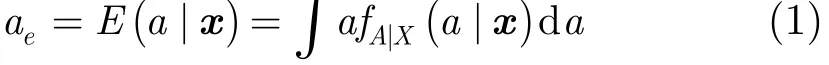
其中后驗概率密度函數為

其中fX|A(x|a)是似然函數，從式(2)可以看出，貝葉斯估計值是數據x和先驗模型參數的函數，即ae=g(x,θ)。也就是說，在貝葉斯估計器的結構中，包含了待估計數據x和先驗模型參數θ。由于數據x是隨機矢量，估計值也是隨機變量，其統計特性與數據x有關。若考慮先驗模型參數的失配問題，即當前探測環境中參數a的統計特性偏離了先驗模型，其概率密度函數為fA(a;?)，那么貝葉斯估計器可以表示為ae=g(x(?),θ)，即貝葉斯估計器應該是數據x、先驗模型參數θ、實際模型參數?的函數，其中參數?是隱含在數據x的統計特性之中，不能直接表示在貝葉斯估計器結構內。在先驗模型失配條件下，貝葉斯估計值ae的統計特性必然受到參數?的影響。估計器性能與估計值的統計性能有關，估計值的ae的統計特性可以用其概率密度函數表示，該密度函數包含有先驗模型參數失配的信息，即ae～fAe(ae,θ,?)。為此可以分析該估計值在當前探測環境下的統計特性，獲得參數?，進一步修正先驗模型參數，實現先驗模型參數與當前探測環境的匹配。

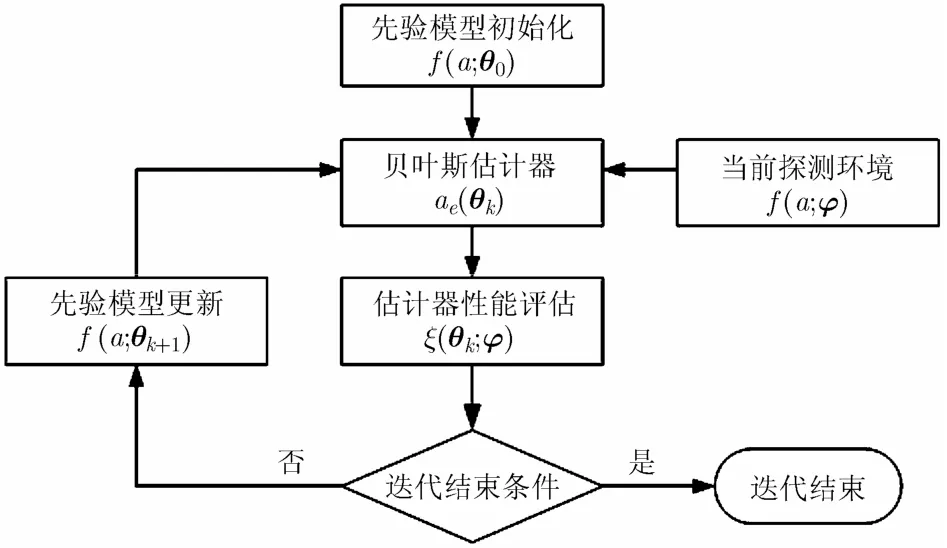
圖 1 基于貝葉斯估計性能的先驗模型感知過程

認知的過程應該是一種迭代的閉環過程，如圖1所示。假定第k次迭代時的先驗模型參數為θk，依據此先驗模型參數，利用式(1)得到貝葉斯估計器ae，該估計器中包含了先驗模型參數θk。將這個估計器應用于當前探測環境，并假定環境中的參數a的實際分布參數為?，且是未知的。一般而言，先驗模型參數與實際分布參數之間必然存在差異，即先驗模型失配。這種失配會影響到估計器的性能。因此可以從估計器性能的分析獲得有關先驗模型失配的信息。參數估計值的統計特性ξ與先驗模型參數θk和實際分布參數?有關。如果可以根據估計性能的分析得到先驗模型參數的更新值θk+1，就可以對先驗模型參數進行更新。隨著迭代的進行，期望的結果是θk=?，這樣就實現了先驗模型與實際場景模型匹配。為了進一步說明上述方法的可行性，本文選擇具有均值先驗的高斯噪聲下的直流信號估計作為研究對象，該方法也可以適合其他的貝葉斯估計器。

3 先驗模型參數失配下的估計性能

本文考慮一種白高斯噪聲下的直流信號的估計問題，假定測量數據為

其中N維矢量x為測量數據，N維矢量w為功率為σ2的高斯白噪聲矢量，并假定噪聲功率已知，則可以得到觀測數據的條件分布：假定待估計參量a的先驗分布滿足均值為μθ，標準差為σθ的高斯分布，即a～N(μθ,)：

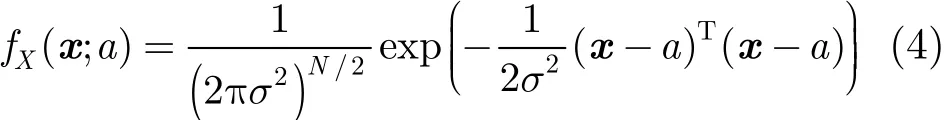
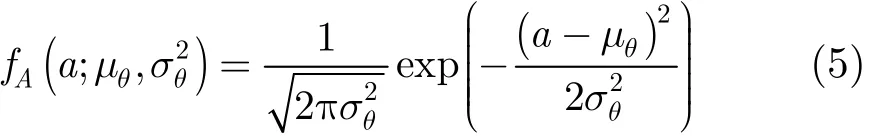
利用式(1)、式(2)可以得到參數a的貝葉斯估計[20]：

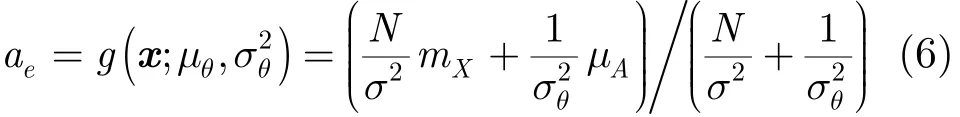
其中mX是觀測數據矢量x中N個元素的算術平均值。從式(6)可以看出，貝葉斯估計器包含有觀測數據的信息(mX)和先驗模型參數(μθ,)。由于x是隨機變量，得到的貝葉斯估計也是隨機量。為此可以分析先驗模型失配條件下的估計值的統計特性。若考慮先驗失配問題，即假定在數據x中，參數a的實際分布是均值μ?，方差的高斯分布，由此可以得到數據x的平均值也滿足高斯分布：

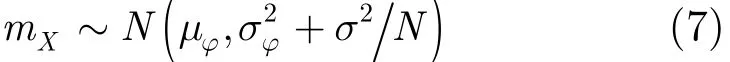
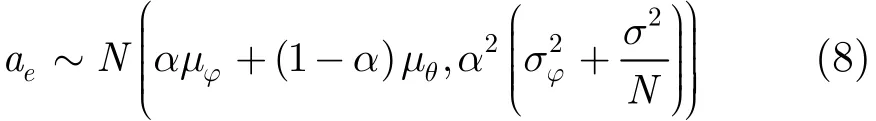
由式(6)可知，估計值ae是mX的線性函數，因此ae也滿足高斯分布：

其中

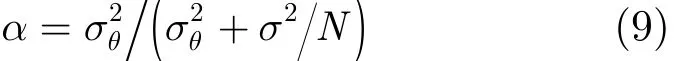
從式(8)可以看出，貝葉斯估計值的統計特性中包含有先驗模型參數(μθ,)，實際模型參數(μ?,)。也就是說，可以通過分析貝葉斯估計值的統計特性，獲得實際模型參數(μ?,)。貝葉斯估計器的性能還可以用均方誤差表示，即

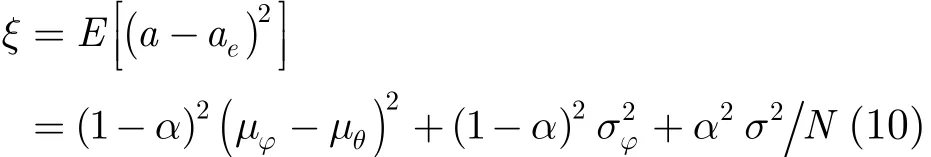
當先驗模型參數匹配時，可以得到最小貝葉斯均方誤差[20]：

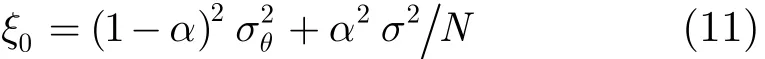
貝葉斯估計的均方誤差可以綜合評估估計器的性能，但在實際情況下，待估計值的真值是未知的，難以獲得均方誤差的測量值。因此貝葉斯估計的均方誤差一般用于理論分析。

4 迭代感知方法

利用在失配條件下的貝葉斯均方誤差進行分析，由式(10)可得到：

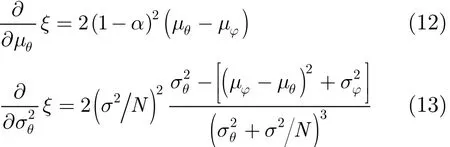
如果令貝葉斯均方誤差對(μθ,)的導數為零，就可以得到(μθ,)=(μ?,)，即對于函數ξ(μθ,)，有且僅有一個極值點(μ?,)，此時先驗模型參數與實際參數模型匹配。這也表明了，對于貝葉斯估計器，若先驗模型與實際模型之間存在失配，貝葉斯均方誤差必然增大，估計性能下降。若先驗模型參數的迭代過程滿足：

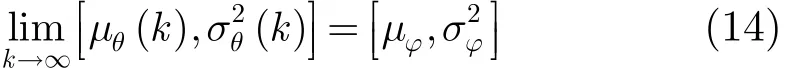
估計器性能隨著迭代次數的增加逐漸得到提高。從式(8)可知，如果獲得了在當前探測環境下的參數a的貝葉斯估計值，該估計值的均值和方差是探測環境模型參數(μ?,)的函數，為此可以通過序貫估計的方法估計出估計值ae的均值和方差：其中k表示迭代次數。再利用貝葉斯估計值的均值/方差與(μ?,)的關系，得到參數(μθ,)的序貫估計：

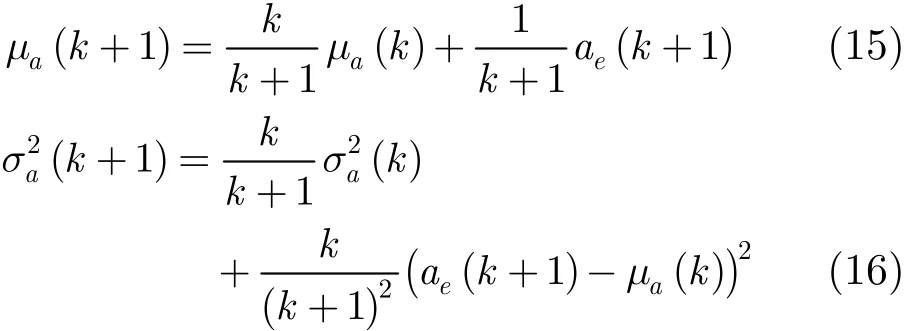
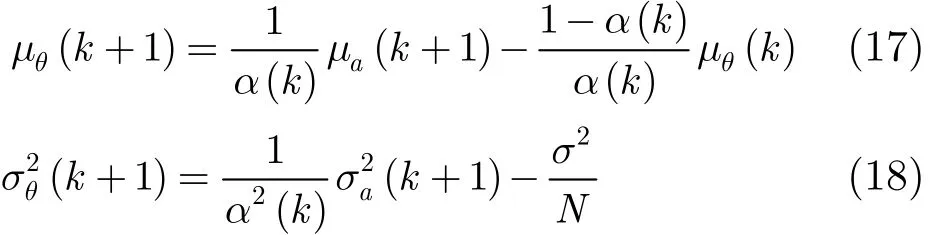
其中

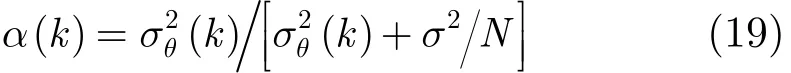
迭代過程是建立在如圖1所示的先驗參數感知框架的基礎上的，給定一個先驗分布參數(μθ(k),(k))，利用式(6)得到參數的估計值。利用式(15)，式(16)得到估計值的均值和方差的序貫估計，即完成貝葉斯估計器的性能評估。利用式(17)，式(18)得到先驗模型參數的序貫估計(μθ(k+1),(k+1))，即通過貝葉斯估計器的性能評估獲得先驗模型參數的更新。上述過程構成一個完整的認知閉環結構，即給定先驗模型參數，設計貝葉斯估計器；將貝葉斯估計器應用于當前探測環境，獲得估計值；通過評估估計器性能獲得先驗模型參數的感知，進而優化先驗模型參數；將此更新后的先驗模型參數用于修正貝葉斯估計器，從而進入另一個閉環認知過程。在這個迭代認知過程中，貝葉斯估計器所使用的先驗信息在不斷地被修正，而修正的方法則來自貝葉斯估計器在當前探測環境中的工作性能評估。這種迭代感知過程與認知雷達的工作方式非常類似，即雷達在持續地理解當前探測環境，并隨著估計器與探測環境交互次數的增加，雷達處理器逐漸與當前探測環境匹配，從而提高認知雷達性能。本文所采用的這種認知迭代過程，并不同于自適應處理方式，在每次迭代過程中，先驗信息模型都會盡可能與當前探測環境匹配，而匹配程度隨著迭代過程逐漸增加，而自適應處理一般不考慮先驗信息的更新問題。迭代的初始值可以任意設定先驗分布參數，但隨著迭代過程的進行，如果待探測環境模型參數是穩定的，那么貝葉斯估計值的均值和方差估計的誤差逐漸減小，最終接近真值。

5 計算機仿真分析

分析迭代感知過程中的先驗模型參數變化情況。在計算機仿真中，首先利用式(3)生成待探測環境數據，其中a的均值和方差為(μ?,)=(3,2)，參數N=8, σ2=1。利用式(6)，式(15)～式(18)等，可以完成先驗模型參數的感知。迭代過程的初始值可以任意選擇，如選擇(μθ(0),(0))=(4,2)。得到的迭代感知值如圖2(a)所示。可以看出，隨著迭代過程的進行，先驗模型參數均逐漸靠近(μ?,)，大約在100次迭代之后，先驗模型參數就已經非常接近(μ?,)。圖2(b)給出了迭代過程的平均收斂情況，利用計算機獨立運行200次，將計算迭代感知值與(μ?,)平均距離。對比可以發現，μθ(k)的收斂速度較快，而(k)的收斂速度較慢。這是因為在式(15)，式(16)中，均值的估計方差要小于方差的估計方差。

在迭代感知過程中，估計器對待估計參數進行估計，利用估計值的統計特性，反演出先驗模型參數，使得其逐漸與待探測環境模型參數相接近。因此在整個感知過程是一個動態的過程。如果待探測環境是平穩的，即模型參數在整個感知過程中不發生變化，從前面的分析可以發現本文給出的迭代過程可以收斂到待探測環境模型參數。如果考慮在迭代過程中，待探測環境中的模型參數發生了變化，那么期望的迭代過程也應該能夠收斂到變化后的待探測環境模型參數。對應的仿真結果如圖3所示。這里的(μ?,)初始值為(3,2)，在迭代次數為1000～3000時，(μ?,)線性變化為(3.5,2.5)。得到的迭代感知值在迭代次數小于1000時，逐漸收斂到(3,2)，一旦待探測環境模型參數發生變化，迭代感知值也會逐漸收斂到新的值(3.5,2.5)。這說明，本文給出的迭代感知方法能夠適合于待探測環境模型參數變化的場景。但與前面的分析結果對比可以發現，收斂的速度較慢，這是因為式(15)，式(16)是針對平穩高斯過程的序貫估計，可以優化該估計方法，提高收斂速度。

再考察本文給出的迭代感知方法在先驗模型失配情況下的迭代感知效果。在圖4(a)中，假定待探測環境中參數滿足3～9之間的均勻分布，那么其均值為6，方差為3。圖4(b)中，假定待探測環境中參數滿足伽馬分布，其中形狀參數為5，尺度參數為2，由此可以得到均值為10，方差為20。可以發現即便存在先驗模型的失配，迭代感知過程仍然可以收斂到待探測環境模型的均值和方差。這是因為本文考慮的估計器本質上僅僅利用了估計值的一、二階統計特性，因此先驗模型匹配的標準退化為一、二階統計特性的匹配問題，而與整個模型是否匹配無關。但是需要指出的是，雖然感知迭代過程可以收斂到待探測環境參數模型的均值和方差，但收斂過程與具體模型有關。

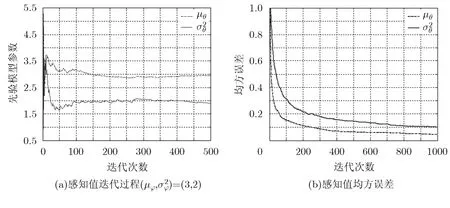
圖2 先驗模型失配條件下估計器的性能分析

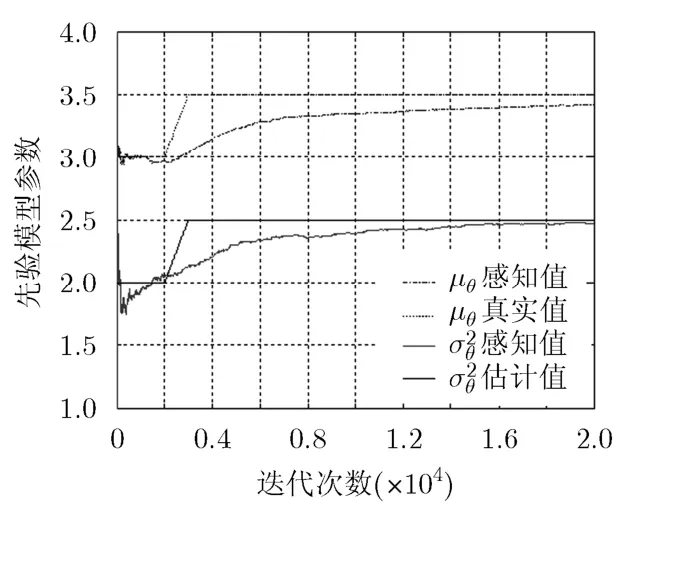
圖3 場景模型參數突變情況下的感知過程

圖4 場景模型失配情況下的感知過程

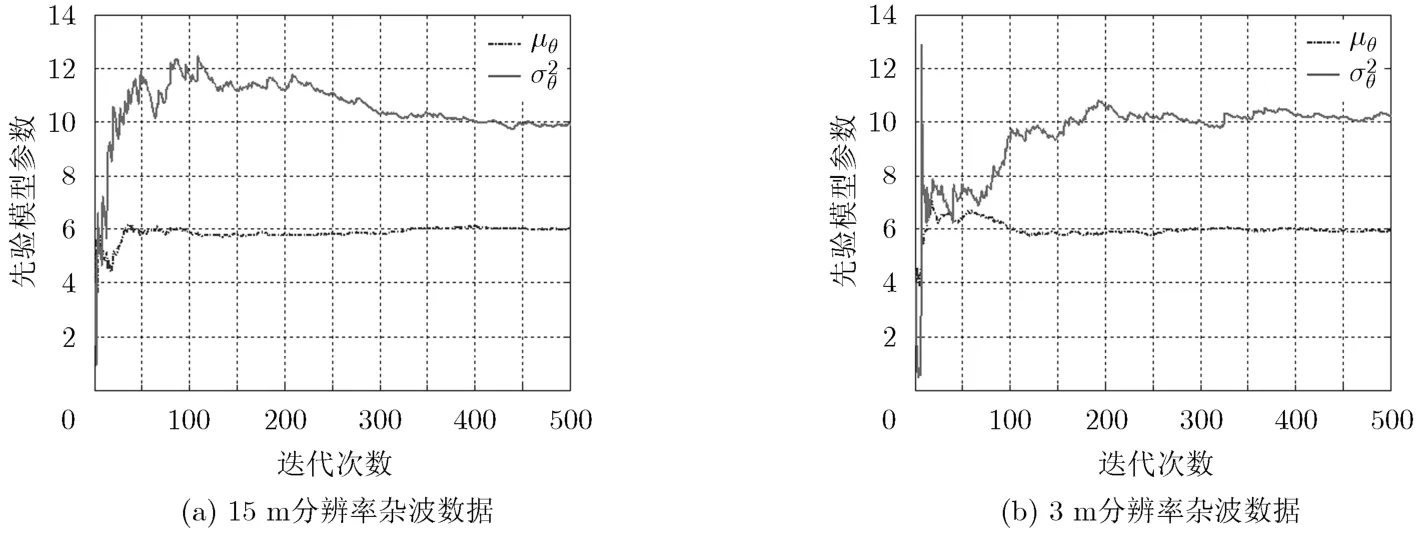
圖5 在實測雜波數據中的感知過程(μ?,)=(6,10)

最后考察本文迭代感知方法在實測雜波數據中的應用問題。本文所采用的數據來自加拿大的McMaster大學自適應系統實驗室的IPIX雷達實測數據。數據采集時間為1998年冬季，采集地點為Grimsby，位于多倫多與Niagara瀑布之間的安大略湖岸邊。網站http://soma.mcmaster.ca/對IPIX雷達參數及其數據有較為詳細的說明。該雷達能夠獲得3種不同距離分辨率的雜波數據，本文選擇的雜波數據對應的距離分辨率為3 m和15 m，對應的數據文件名稱為19980223_171533_ANTSTEP和19980223_170435_ANTSTEP。該數據屬于X波段海雜波數據，數據的統計特性偏離的高斯統計特性。該數據共有60000個脈沖、34個距離分辨單元構成的基帶信號。本文選擇的極化方式為HH，即發射和接收同為水平極化。選擇第17個距離單元的雜波數據。在每個雜波矢量上疊加一個均值和方差滿足(μ?,)=(6,10)的高斯信號，類似于對雜波中起伏目標的參數估計問題。利用本文給出的迭代感知方法，可以得到先驗模型參數隨著迭代次數的變化情況，如圖5所示。從仿真結果來看，隨著迭代過程的進行，先驗模型參數(μθ,)能夠逐漸接近(μ?,)，這說明，即使在非高斯雜波中，利用本文給出的迭代感知方法仍然可以獲得當前探測環境模型參數。

6 結束語

認知雷達的主要功能包括信號檢測、估計、跟蹤、識別等。而在認知框架下，雷達能夠不斷地對當前環境進行探測，完成對未知場景的認知。這個認知過程應該是交互的、迭代、收斂的過程。對于貝葉斯估計器，先驗信息代表了對雷達觀測歷史的記憶，其與當前探測環境可能不一致。在貝葉斯框架下，認知過程應該是先驗信息的修正過程，使得先驗信息模型逐漸與待探測環境模型相一致。

貝葉斯框架下的先驗模型感知可以利用貝葉斯估計器和貝葉斯檢測器。本文首先給出了貝葉斯估計器的先驗模型參數感知的一般性框架。在這個框架下，針對高斯噪聲下的具有高斯先驗的幅度的貝葉斯估計器，推導了在先驗模型參數失配條件下的估計性能，利用計算機仿真分析了該估計器在先驗模型參數失配下的穩健性和敏感性。從穩健性分析結果可知，先驗模型參數的失配必然導致貝葉斯均方誤差增大，即估計性能變差。分析了迭代感知過程的收斂情況，并分別考慮了待探測環境模型參數突變、先驗模型失配、實測非高斯雜波下的感知迭代過程，仿真分析表明，本文給出的迭代感知過程具有很好的穩健性，能夠逐漸收斂到待探測環境模型參數。

認知雷達還是一個較為新穎的研究方向，將認知的過程引入到雷達的信號處理中，還有很多問題。認知過程包括認知發射和認知接收兩個部分，本文主要集中在認知接收處理方面，沒有考慮到發射參數的優化問題。本文討論了的重點是在貝葉斯框架下的一種基于處理性能評估的先驗模型參數的迭代感知方法，其迭代過程收斂速度、收斂唯一性與先驗模型本身有關系，是下一步研究的重點，將本文給出了感知框架應用于其它貝葉斯估計器也是值得研究的。

[1] Berger J O. Statistical Decision Theory and Bayesian Analysis[M]. New York: Springer, 1985: 1-77.

[2] 茆詩松, 湯銀才. 貝葉斯統計[M]. 第2版, 北京: 中國統計出版社, 2012: 35-44.

Mao Shi-song and Tang Yin-cai. Bayes Statistics[M]. Second Edition, Beijing: China Statistics Press, 2012: 35-44.

[3] Gini F and Rangaswamy M. Knowledge-based Radar Detection, Tracking, and Classification[M]. New York: Published by John Wiley & Sons, Inc., 2008: 102-211.

[4] Moya J C and Maio A D. Experimental performance analysis of distributed targets coherent radar detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2216-2238.

[5] Ollila E, Tyler D E, Koivunen V, et al.. Compound Gaussian clutter modeling with an inverse Gaussian texture distribution[J]. IEEE Signal Processing Letters, 2012, 19(12): 876-879.

[6] Abdelaziz M E M, Chonavel T, Aissa-El-Bey A, et al.. Sea clutter texture estimation: exploiting decorrelation and cyclostationarity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 726-742.

[7] Sangston K J, Gini F, and Greco M S. Coherent radar target detection in heavy-tailed compound Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 64-77.

[8] Gao Y, Liao G, Zhu S, et al.. A persymmetric GLRT for adaptive detection in compound Gaussian clutter with random texture[J]. IEEE Signal Processing Letters, 2013, 20(6): 615-618.

[9] Bandiera F, Besson O, and Ricci G. Knowledge-aided covariance matrix estimation and adaptive detection in compound Gaussian noise[J]. IEEE Transaction on Signal Processing, 2010, 58(10): 5390-5396.

[10] Bandiera F, Besson O, and Ricci G. Adaptive detection of distributed targets in compound-Gaussian noise without secondary data: a Bayesian approach[J]. IEEE Transactions on Signal Processing, 2011, 59(12): 5698-5708.

[11] Tang B, Tang J, and Peng Y N. Performance of knowledge aided space time adaptive processing[J]. IET Radar, Sonar & Navigation, 2011, 5(3): 331-340.

[12] Greco M, Stinco P, and Gini F. Impact of sea clutter nonstationarity on disturbance covariance matrix estimation and CFAR detector performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1502-1513.

[13] Bandiera F, Orlando D, and Ricci G. Advanced Radar Detection Schemes under Mismatched Signal Model[M]. Synthesis Lecture on Signal Processing, New York: Morgan & Claypool Publishers, 2009: 15-24.

[14] 唐波, 張玉, 李科. 基于先驗知識及其定量評估的自適應雜波抑制研究[J]. 航空學報, 2013, 34(5): 1174-1180.

Tang Bo, Zhang Yu, and Li Ke. Adaptive clutter suppression research based on prior knowledge and its accuracy evaluation[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1174-1180.

[15] 鄒鯤, 廖桂生, 李軍, 等. 基于Bayes框架的復合高斯雜波下穩健檢測[J]. 電子與信息學報, 2013, 35(7): 1551-1560.

Zou Kun, Liao Gui-sheng, Li Jun, et al.. Robust detection in compound Gaussian clutter based on Bayesian framework[J]. Journal of Electronics & Information Technology, 2013, 35(7): 1551-1560.

[16] 鄒鯤, 廖桂生, 李軍, 等. 非高斯雜波下知識輔助檢測器敏感性分析[J]. 電子與信息學報, 2014, 36(1): 181-186.

Zou Kun, Liao Gui-sheng, Li Jun, et al.. Sensitivity analysis of knowledge aided detector in non-Gaussian clutter[J]. Journal of Electronics & Information Technology, 2014, 36(1): 181-186.

[17] 鄒鯤, 廖桂生, 李軍, 等. 非高斯雜波下知識輔助檢測的認知方法[J]. 電子學報, 2014, 42(6): 1047-1054.

Zou Kun, Liao Gui-sheng, Li Jun, et al.. Cognitive method for knowledge aided detection in non-Gaussian clutter[J]. Acta Electronica Sinica, 2014, 42(6): 1047-1054.

[18] Haykin S. Cognitive Dynamic Systems, Perception-action Cycle Radar, and Radio[M]. Cambridge: Cambridge University Press, 2012: 201-230.

[19] Zhang X and Cui C. Signal detection for cognitive radar[J]. Electronics Letters, 2013, 49(8): 559-560.

[20] Kay S M. Fundamental of Statistical Signal Processing, Volume I: Estimation Theory[M], New Jersy: Pearson Education Inc., 1993: 360-365.

鄒 鯤： 男，1976年生，講師，從事雷達信號處理、統計信號檢測及其在雷達、導航方面的應用研究.

張 斌： 男，1968年生，教授，從事通信、雷達、導航系統理論、自適應信號處理方面的研究.

王曉薇： 女，1972年生，副教授，從事軍用導航裝備理論研究.

林澄清： 男，1986年生，工程師，從事軍用導航裝備應用研究.

Iterated Cognition Method for Prior Model Parameters of Bayesian Estimator

Zou Kun①Zhang Bin①Wang Xiao-wei①Lin Cheng-qing②

①(School of Information and Navigation, Air Force Engineering University, Xi'an 710077, China)

②(94816 Troops of PLA, Putian 351100, China)

Smart use of prior information is one of effective approaches to improve the performance of Bayesian estimator. At the design stage of Bayesian estimator, the prior model parameters must be specified, but these parameters may not be identical with parameters of environment at the applicant stage. The mismatched prior model can result to the performance degradation of Bayesian estimator. In this paper, a general framework of prior model parameters cognition based on the estimator performance is given at first. Base on the framework, for a Bayesian estimator of DC signal in WGN, the estimation performance is analyzed, and an iterated cognition method of prior model parameters is proposed. The computer simulation is used to analyze the sensitivity and robustness of the estimator under the mismatched prior model condition, and the iterated cognition procedure under different conditions. The computer simulation results show that, the feedback from the estimation performance to the prior model parameters is obtained with the cognitive method proposed in this paper, and the prior model can be matched with the current environment model after the repeated interactions between the estimator and environment.

Radar signal processing; Bayesian estimator; Mismatched prior; Robustness; Sensitivity; Iterated cognitive method

TN957.51

： A

：1009-5896(2015)06-1402-07

10.11999/JEIT141012

2014-07-28收到，2015-02-28改回

國家自然科學基金(61273408, 61302153)和航空創新基金資助課題

*通信作者：鄒鯤 wyyxzk@163.com