一種改進PSO-LSSVM算法在鍋爐燃燒優化中的應用

童 曉，孫衛紅，李 強

(1.中國計量學院 機電工程學院，杭州 310018；2.新疆維吾爾自治區特種設備檢驗研究院實驗中心，烏魯木齊 830011)

0 引言

鍋爐燃燒是一個非常復雜的非線性過程，而鍋爐效率和NOX排放量是表征鍋爐燃燒是否完全的重要指標，也是目前鍋爐行業節能減排工作重要指標。實際運行過程中很難根據經驗或調試結果將鍋爐燃燒工況調整到一個理想狀態，所以建立適當模型并結合合適的優化算法獲得可行的鍋爐燃燒運行參數是很有意義的。

研究開發者已對鍋爐燃燒優化方法進行了研究。利用人工神經網絡(ANN)[1～3]結合遺傳算法可實現鍋爐的燃燒優化，但網絡結構有一定的難度，存在過學習及易陷入局部極小點等缺點；而基于統計理論的支持向量機(SVM)與優化算法結合有很好的效果[4]，但是SVM計算復雜[5]，在實際應用中有很大的限制性。最小二乘支持向量機(LSSVM)是在SVM的基礎上用等式約束替代不等式約束，避免了求解二次回歸問題[6]，以任意精度逼近非線性系統，是非線性系統建模的有力工具[7～9]。通過文獻中比較可知，LSSVM模型的精度更高，且在模型訓練和收斂速度上較其他模型要快。

本文利用LSSVM分別建立鍋爐燃燒特性模型，并對模型訓練和校驗，結果表明LSSVM模型可很好地表示鍋爐主要物理量之間關系，具有良好的泛化性。再結合改進粒子群優化算法對鍋爐運行工況進行尋優，為鍋爐使用單位的燃燒優化調整得到高效低NOX提供有效的手段。

1 LSSVM建鍋爐燃燒過程模型

1.1 LSSVM

鍋爐燃燒過程是一個高度非線性的復雜動態過程，其建模一般采用ANN和SVM等。ANN建模需要大量樣本數據，無法避免出現局部極小和過度擬合的現象，且收斂速度得不到保證；SVM建模方法用結構風險最小化代替了經驗風險最小化[10]，克服了ANN建模存在的缺點[11]。LSSVM是標準支持向量機理論[12]的一種擴展利用，把求解二次規劃問題轉化為求解線性方程組問題，提高了求解問題的速度從而縮短了求解時間。

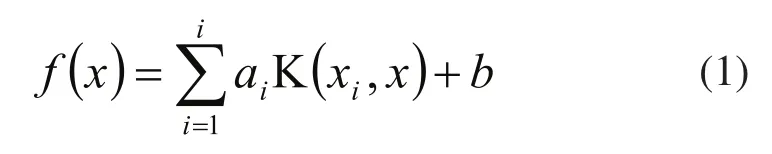
1.2 LSSVM模型的輸入和輸出

LSSVM模型是以歷史數據作為訓練樣本，樣本輸入直接影響模型精度。根據優化目標結合鍋爐實際燃燒特性選取必要的變量經數據預處理后作為模型訓練樣本。鍋爐燃燒特性LSSVM模型如圖1所示。

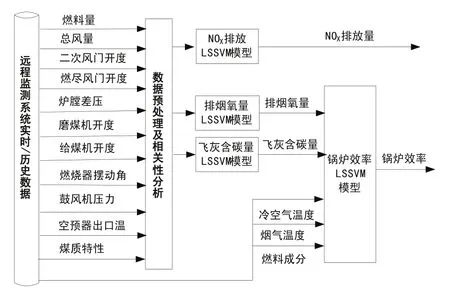
圖1 鍋爐燃燒特性LSSVM模型

調用數據庫中必要運行參數作為模型輸入，通過數據預處理后進行訓練和測試。如圖1所示，模型結構分3層，輸入層為30個運行操作量的輸入，中間層得NOX排放量、飛灰含碳量和排煙氧量3個輸出點，輸出層是包括飛灰含碳量、排煙氧量等7個輸入點，最后獲得一個鍋爐效率的輸出點。

1.3 LSSVM模型仿真結果分析

本文利用文獻[1,2]的12組試驗工況數據建立LSSVM模型。取工況1～11數據作訓練樣本，訓練LSSVM鍋爐特性模型，并用工況12進行驗證。

首先對樣本數據進行歸一化處理，歸一到[0,1]區間，歸一化公式為：

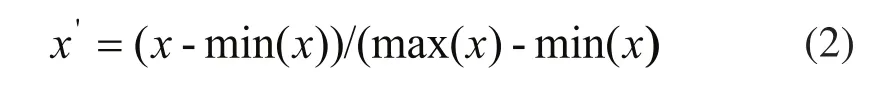
其中x和x'分別是樣本歸一化前、后的值。設置LSSVM模型的懲罰因子和徑向基核參數分別為C=100，利用交叉驗證優化參數后對模型進行訓練得到歸一化后的預測值，再進行反歸一化計算出預測值和實際值的相對誤差，圖2(a)、(b)和(c)分別表示NOX排放量、飛灰含碳量和排煙氧量的預測值和實測值對比圖。由結果可知對于前11組訓練樣本，模型輸出值與實測值基本接近，對工況12的NOX排放量、飛灰含碳量和排煙氧量的預測值分別為788.55mg/m3、1.167%和3.13808%，相對誤差分別為0.16304%、0.5893%和1.58942%。

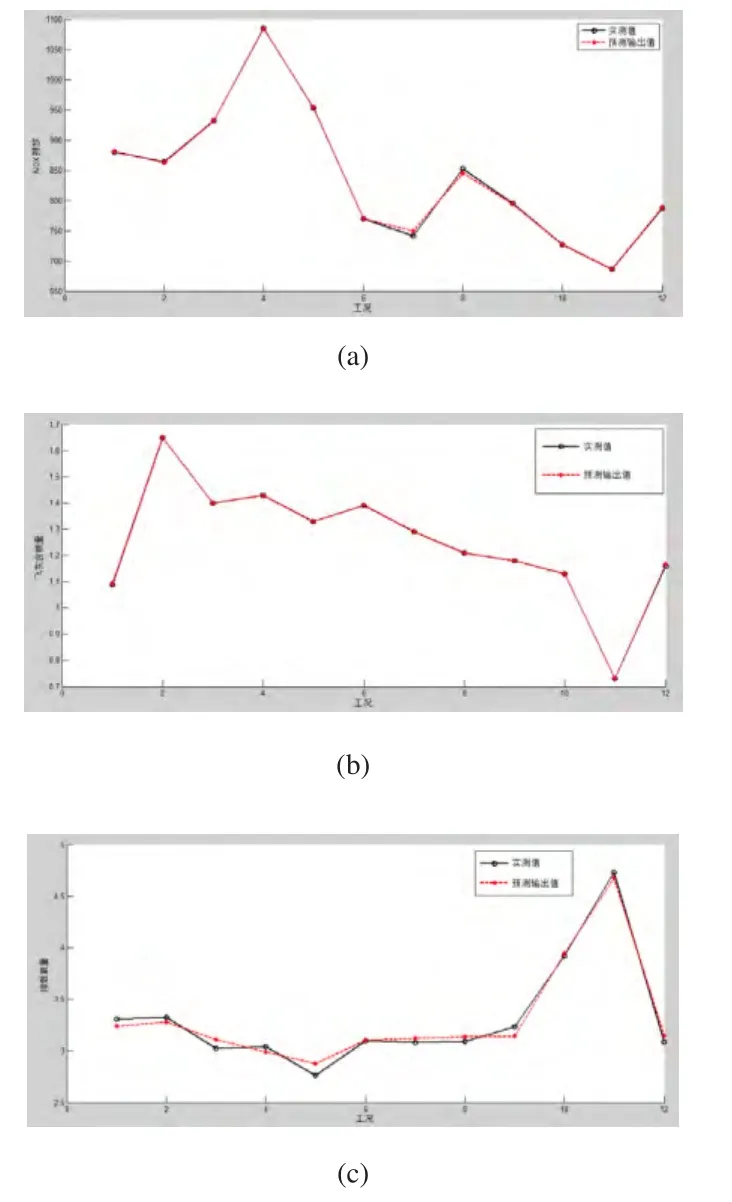
圖2 LSSVM模型輸出值和實測值對比

與文獻[2]神經網絡預測結果比較如表1所示。表明對于同樣測試樣本，神經網絡的預測相對誤差比LSSVM要大，說明LSSVM具有良好的泛化能力，預測結果更為準確。

鍋爐效率是表征鍋爐運行經濟性的重要技術指標。利用鍋爐熱效率模型，計算結果如表2所示。

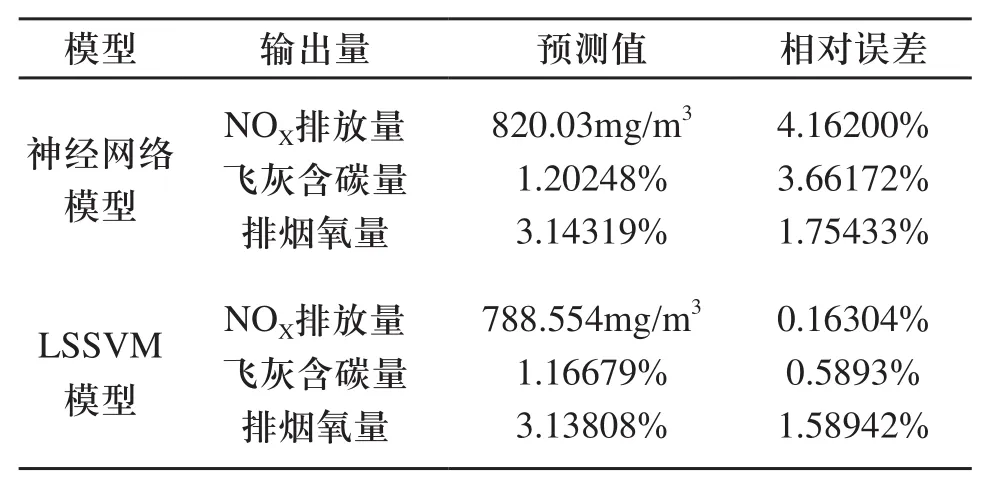
表1 2種模型的預測結果比較

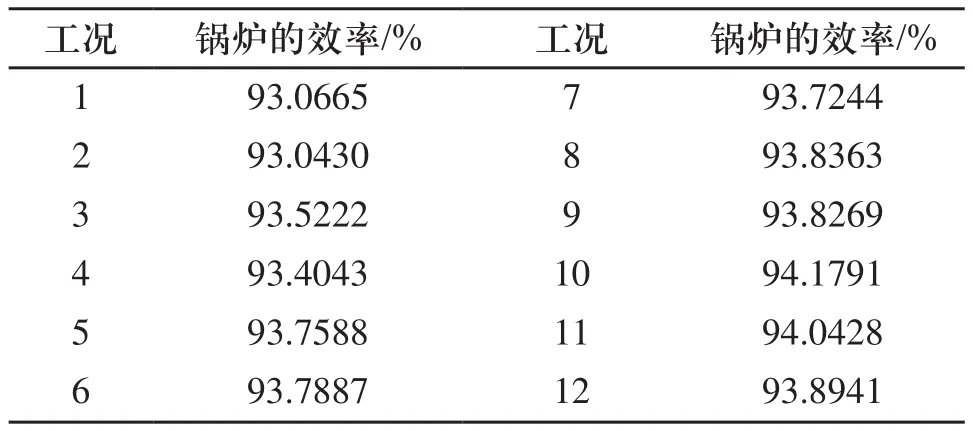
表2 鍋爐熱效率響應特性

2 改進PSO優化鍋爐燃燒工況

控制參數尋優問題指從大量數據中搜索出最優的一個或者幾個的組合使系統的性能指標要求取得最優的數據。本文先討論粒子群優化算法(PSO)并對算法提出改進，通過對可調參數優化配置改善鍋爐燃燒工況。本文選取工況1進行優化調整。

2.1 PSO算法簡介

粒子群優化算法(PSO)是一種隨機搜索、并行的優化算法[9]，與遺傳算法比，它沒有選擇、交叉、變異等操作，通過粒子在解空間追隨最優粒子進行搜索，快速有效的解決預測控制器設計中目標函數優化問題，有較強的全局收斂能力和魯棒性等特點。

本文針對非線性多目標優化問題，根據送風量和燃料量隨著鍋爐負荷的變化而變化，采用粒子群算法對送風調節系統最佳的氧量設定進行大范圍的全局搜索。標準PSO中粒子在搜索空間的速度和位置根據下面公式確定[15]：

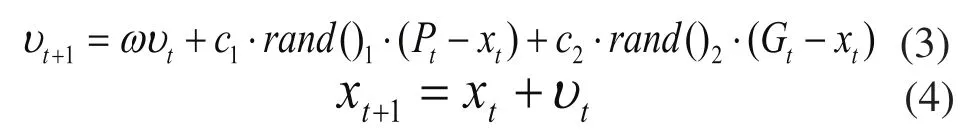
2.2 對PSO算法的改進

為克服PSO算法固有飛行后期失去粒子多樣性的不足及過早收斂于局部最優值，根據PSO改進方法[15]，針對本文內容將粒子狀態更新策略作改進：先任選兩個粒子群，一個粒子群的粒子采用增加擾動因子n的策略來變化粒子位置和速度，當粒子搜索到全局最優適應值連續n步迭代無更新，則重置粒子速度或位置，強迫粒子跳出局部極小點；另一個粒子群的粒子，則在迭代中前期使粒子在搜索時只追逐自己搜索到的最優值，而不追逐當前的全局最優值，在后期則重新由式(3)、式(4)進行運行變化，目的是避免粒子追逐局部最優極值，從而錯過全局最優極值；其他群體粒子仍根據式(3)、式(4)進行變化。優化流程圖如圖3所示。

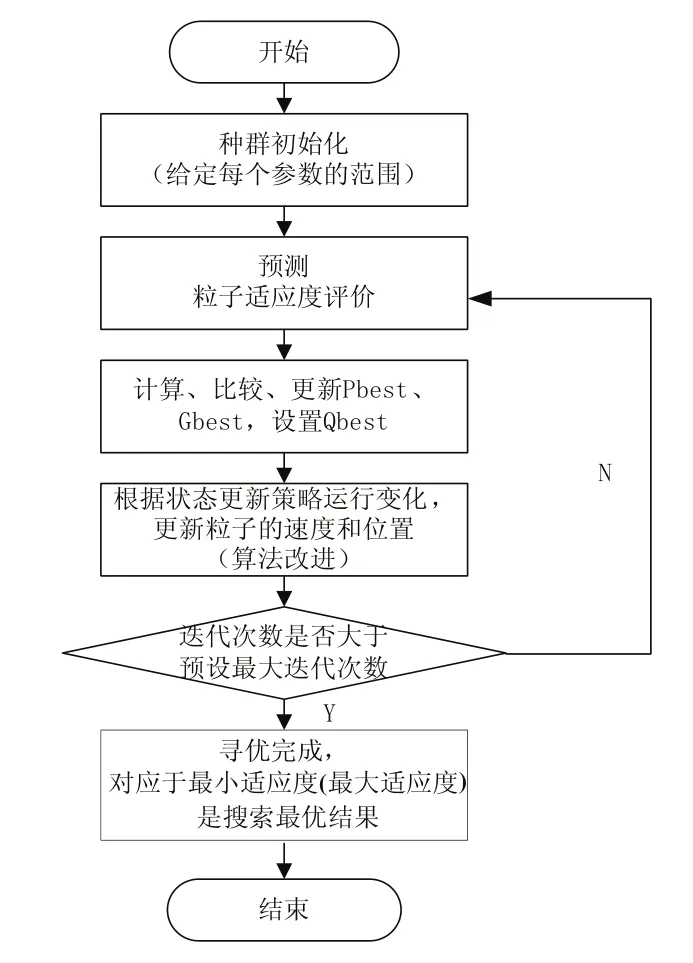
圖3 粒子群優化流程圖

改進PSO是利用底層的每個粒子的獨立搜索來保證搜索可在大范圍內進行，同時又利用頂層粒子群追逐當前全局最優點來保證算法的收斂性，兼顧優化過程的精度和效率。

3 鍋爐燃燒多目標優化實例仿真

根據實際情況分析可知，降低NOX排放量與提高鍋爐效率兩者是一種矛盾關系，為兼顧兩方面影響需調整運行參數達到燃燒優化。過程為：

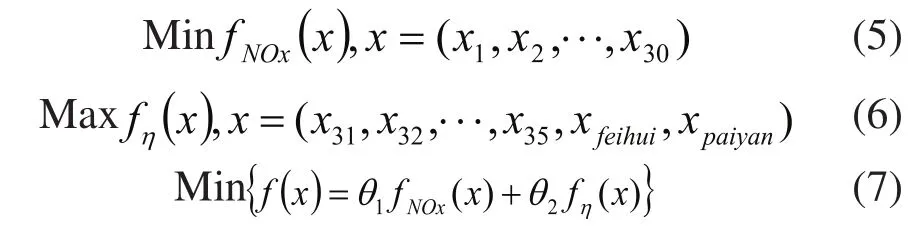
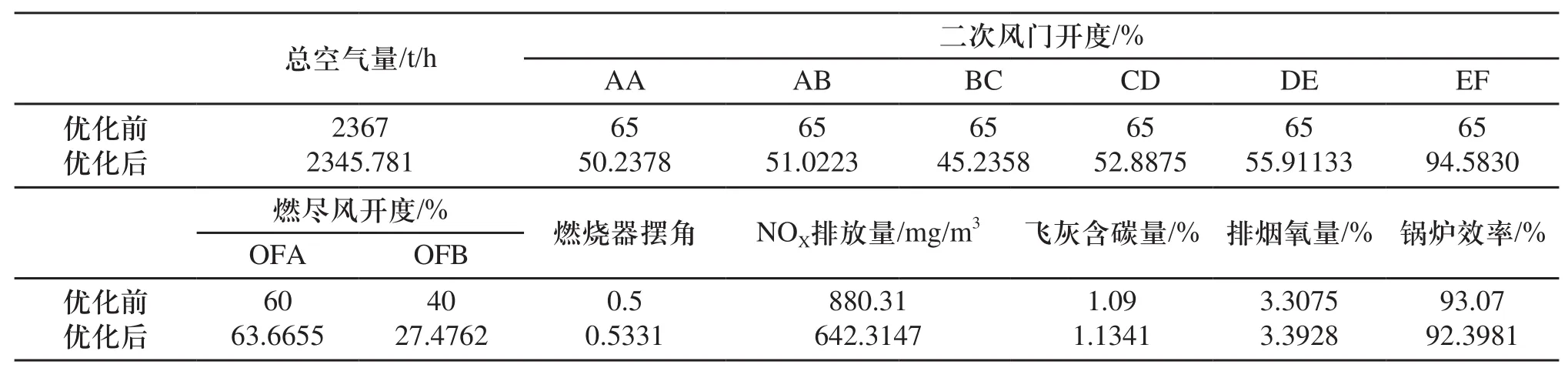
表3 優化前后對應鍋爐運行參數及輸出結果

PSO參數設置：種群粒子數為50；算法迭代進化次數為200；慣性權值采用加速因子算法設置為連續40次迭代中函數的值沒有變化或達到了最大設定值則優化終止。

優化輸出結果與工況1參數相比較如表4所示。由表格可以看出，在該優化策略下，NOX排放量下降到642.3147mg/m3。雖然鍋爐的熱效率有所下降，但達到預設的效果。結果表明，LSSVM與改進的PSO算法結合是一種可行的鍋爐燃燒優化方法。

4 結束語

通過上述建模和優化調整表明，LSSVM算法在建立鍋爐燃燒特性模型方面有良好性能，可很好預測和表示鍋爐燃燒特性關系；改進PSO在鍋爐燃燒優化問題上有效的降低了NOX排放，為鍋爐高效低NOX的實現提供了一種有效方法，為鍋爐燃燒優化控制奠定基礎。如果對模型內部參數進行修正將會得到更好的優化品質。

[1]周昊,朱洪波,岑可法.基于人工神經網絡和遺傳算法的火電廠鍋爐試試燃燒優化系統[J].動力工程,2003,23(5):2665-2669.

[2]王培紅,李磊磊,陳強,董益華.人工智能技術在電站鍋爐燃燒優化中的應用研究[J].中國電機工程學報,2004,24(4):184-188.

[3]凡榮榮,姚翠蘭,楊巨生,等.基于PSO優化鍋爐氮氧化物的排放[J].熱力發電,2012,41(8):28-31.

[4]費洪曉,黃勤徑,戴戈,肖新華.基于SVM與遺傳算法的燃煤鍋爐燃燒多目標優化系統[J].計算機應用研究,2008,25(3):811-813.

[5]陳冰梅,樊曉平,周志明,李雪榮.支持向量機原理及展望[J].制造業自動化,2010,32(12):136-138.

[6]Suykens J A K,Vandewalle J.Least square support machine classfier[J].Neural Processing Letters,1999,9(3):293-300.

[7]Esen H, Ozgen F, Esen M.Modeling of a new solar air heater through least square support vector machine[J].Expert Systems with Applications,2009,36(7):10673-10682.

[8]顧燕萍,趙文杰,吳占松.基于最小二乘支持向量機的電站鍋爐燃燒優化[J].中國電機工程學報,2010,30(17):91-97.

[9]龍文,梁昔明,龍祖強.基于混合PSO優化的LSSVM鍋爐煙氣含氧量預測控制[J].中南大學學報(自然科學版),2012,43(3): 980-985.

[10]朱樹元,張仁杰.支持向量機核函數選擇的研究[J].科學技術與工程,2008,8(16):4513-4517.

[11]Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer Verlag,1995:123-180.

[12]Nello Cristianini, John Shawe-Taylor.支持向量機導論[M].李國正,王猛,曾華軍譯.北京:電子工業出版社,2004.

[13]楊海燕,周永權.一種支持向量機的混合核函數[J].計算機應用,2009,29:173-178.

[14]Keerthi S S, Lin C J.Asymptotic behaviors of support vector machines with Gaussian kernel[J].Neural Computation, 2003, 15(7):1667-1689.

[15]覃建波,陸安山.粒子群算法的改進研究[J].欽州學院學報,2011,26(6):20-24.